软弱破碎围岩隧道炭质页岩蠕变特性试验研究

刘 钦，李术才，李利平，原小帅，赵 勇

（1. 长安大学 建筑工程学院，西安 710061；2. 山东大学 岩土与结构研究中心，济南 250061；3. 郑州市轨道交通建设管理办公室，郑州 450000；4. 铁道部工程设计鉴定中心 桥隧咨询部，北京 100844）

1 引 言

根据国民经济和社会发展战略部署，高速增长的资源流动性和速度需求使得我国交通网建设、能源开采、油气储备等大型基础建设活动近年来呈现迅猛的发展态势[1－2]。我国是个多山的国家，山区主要分布于西南地区，因此，基础建设过程中所规划的长、大、深隧道难免要穿过软弱破碎地层，而软弱破碎地层的岩体的变形往往具有累进性扩展和时间效应两大特征，给施工建设造成极大的困 难，也给隧道设计、施工带来一系列的问题。岩体工程的失稳和破坏绝大多数都与岩石的蠕变特性有关[3－6]，为了保证软弱破碎围岩隧道岩土工程施工安全及长期稳定性，必须考虑岩石的蠕变特性[7－9]。

本文以贵广(贵阳至广州)铁路天平山隧道软弱破碎围岩地段炭质页岩为研究对象，采用分级加载的方式，对该岩石进行了常规三轴压缩试验和三轴压缩蠕变试验。基于试验成果，分析了炭质页岩的蠕变力学特征，建立了黏弹塑性应变软化蠕变力学模型，并推导了该力学模型的本构方程，借助MATLAB程序中的最小二乘工具，对模型的参数进行了辨识。结果显示，本文模型能够较好地描述依托工程页岩蠕变过程，且能够反映其蠕变机制。

2 工程概况

在建的贵广高速铁路是我国重点支撑性基础设施项目。贵广铁路是我国西南地区一条重要的战略要道，全长857 km，途径我国西南的贵州省、广西壮族自治区，终于南部沿海省份广东省。贵阳至广州铁路天平山隧道(DK366+870～DK380+875)，全长14005 m，最大埋深775 m，为双线单洞隧道，设计时速为250 km。隧道洞身穿过奥陶系、寒武系地层，以砂岩、页岩为主，局部段落为页岩夹炭质页岩，砂岩裂隙发育，且洞身段穿越4条区域性大断层，地下水发育，炭质页岩属软弱围岩，尤其当厚层炭质页岩、构造发育、岩体破碎、富含地下水时，因围岩强度低、开挖后风化快、透水性弱、亲水性强，浸水后容易产生较大的塑性变形甚至蠕变，在施工中可能引起较大的挤压性变形。当隧道开挖前处在高围压状态时，尚具有较高的强度和稳定性；当围压降低、围岩应力差增大时，结构面张开或滑移，围岩整体强度和模量降低，表现出显著的结构蠕变特点。

图1为天平山隧道开挖至软弱变形段处洞内揭露围岩。

图1 天平山隧道洞内揭露围岩Fig.1 Exposed rock of Tianpingshan tunnel

3 炭质页岩力学特性试验

3.1 试验过程及试验结果

试验中所用的炭质页岩取自天平山隧道试验里程段，在现场进行简单切割之后，采用土工布包裹，运输至试验室。经过 ZS-100钻孔取样机水钻法钻取岩芯，岩石切割机切割，双端面磨平机打磨等几道工序，制成直径为50 mm，高100 mm的圆柱形岩样，符合国际岩石力学学会规定的高径比2.0～2.5的要求。试件加工精度按我国《工程岩体试验方法标准》[16]执行。

本次试验采用等侧向压力条件下的三轴压缩试验（σ2=σ3）。将安装完成的试块置入三轴室之后，对三轴室充油，打开围压控制阀，施加围压，围压分别采用0、3、5 MPa，最后一次性连续加载轴压直至试件破坏，加载速度控制在0.5 MPa/s。试验机自动记录试验过程的应力和变形值，采样间隔设置为0.02 min，试验过程中蠕变仪全程记录试验过程中试件的应力、变形等数据。三轴压缩试验过程及部分试件破坏形态见图2。图3为页岩试件在不同围压条件下的瞬时三轴应力-应变曲线。

图2 三轴压缩试验过程及部分试件破坏形态Fig.2 Triaxial compression test process and failure modes of some tests

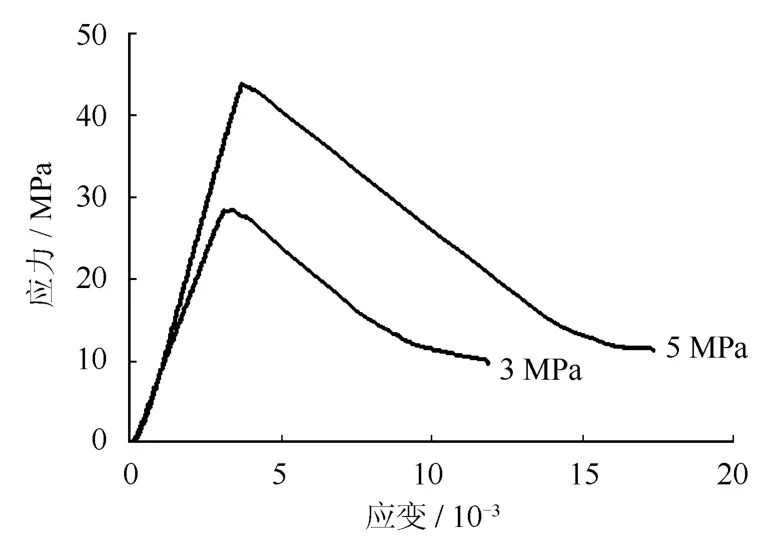
图3 不同围压下页岩试件的应力-应变曲线Fig.3 σ-εcurves of shale samples under different confining pressures

由于本次三轴试验在围压较低情况下进行，试验岩样呈现出明显的脆性破坏，表现出较明显的应变软化特性，相比3 MPa围压和5 MPa围压条件下的峰后软化段曲线变化平缓，并且峰值强度和残余强度均有所提高。岩石在三向应力状态下是受主应力的作用，主平面为受压平面，试件表面无剪应力作用，故当轴向压力增大时，岩石试块一方面会沿着最大主应力方向的微裂纹产生拉裂且延伸，另一方面，由于围压作用迫使其沿着最大主应力斜交方向产生滑动，使岩石试块产生以张裂为主的拉剪的宏观破坏[11－14]。岩石强度特性随着应力状态的改变而变化，相比单轴应力状态，三向应力状态下岩石的强度较高。根据试验结果，3 MPa围压条件下，页岩试件的极限抗压强度在 20～30 MPa之间；5 MPa围压条件下，页岩试件的极限抗压强度在40～50 MPa之间。

岩石的室内蠕变试验通常有两种加载方式[15]：分别为加载和分级加载。前者是在同样的仪器和试验条件、不同的应力水平情况下，对同一种岩样进行试验，目的是为了得到一组不同应力水平下的蠕变全过程曲线。从理论上说，这种方法较符合蠕变试验的要求，但却难以保证试验条件完全相同。后者是在同一岩样上逐级施加不同的应力水平，在一级应力水平下蠕变达到稳定或经历既定的时间后，将应力水平增加至下一级，直至岩样破坏。这种方法不仅节省了岩样和仪器的数量，而且能够避免因岩石性质不均匀导致的试验结果的离散，但其缺点在于分级加载中上一级荷载应力水平会对岩样造成不同程度的损伤。总之，两种方法各有所长。目前室内蠕变试验普遍采用分级加载的方式。

本试验采用分级等围压三轴压缩蠕变试验，轴向加载应力水平取 5～8级。根据岩石的单轴抗压强度值，确定每级围压下岩样三轴蠕变分级加载试验的应力水平。由于时间和成本等因素，本次试验对两块试件分别进行不同围压下的三轴蠕变试验。

在以往的三轴压缩蠕变试验中，围压值一般取值较大，而现有的隧道支护方式和支护结构对围岩所提供的径向力较小，故研究低围压条件下岩石的蠕变规律对软岩隧道的支护有重要的实践意义[16]，因此，本次对标准试件进行了围压为3、5 MPa的三轴蠕变试验。对于不同的围压，均按单轴压缩蠕变的轴向加荷数值依次分级施加主应力差，即(σ1-σ3)=15%σc、30%σc、45%σc、60%σc、75%σc、90%σc、105%σc、120%σc，… 的比例分级加载，每级荷载稳定的时间为3～5 d。越接近蠕变的破坏阶段时，其轴向加荷数可酌情减少，得到在不同围压下反映岩石蠕变的初期阶段、蠕变的发展阶段和蠕变的破坏阶段所对应的一系列不同主应力差，以及对应的轴向应变-时间以及径向应变-时间的关系曲线。在试件加载过程中，首先给试件一个较小的轴向应力，以保证试件与压力机的压头接触密切，然后逐渐增大围压，同时加载轴向压力，围压加载结束后，将轴向位移和横向位移传感器的数据清零，保持恒定的围压以位移控制方式增大轴向压力直到试件破坏。

图4、5分别为炭质页岩在围压 3 MPa和5 MPa分级荷载条件下的单轴蠕变曲线。图中，图4(a)、图 5(a)为岩样试验峰值前的应力-应变曲线，图4(b)、图5(b)为应变随时间变化曲线。由图4(a)、5(a)可见，在3、5 MPa围压条件下，页岩试样在较低应力水平时，蠕变现象不明显，随着应力水平的增大，蠕变现象逐渐明显，在图中表现为“平台”，即应力水平增大时，平台的长度明显变长，说明了应力不变的情况下应变在持续增长。由图4(b)、5(b)可见，本试验中的围压条件下，页岩试件只出现了减速蠕变和等速蠕变阶段，在更高的应力水平下，试件并未出现加速蠕变的情况，从变形加剧直至溃屈，历时很短，但围压在一定程度上，提高了岩石的屈服强度，弹性模量亦有随着围压增大的趋势。因此，在工程实践中，通过支护措施和加固手段来增大围压，能够降低岩体的蠕变程度，进而提高岩体工程的稳定性和安全性。

图4 3 MPa围压分级荷载下页岩轴向蠕变曲线Fig.4 Shale axial creep curves under changeable load with confining pressures of 3 MPa

图5 5 MPa围压分级荷载下页岩轴向蠕变曲线Fig.5 Shale axial creep curves under changeable load with confining pressures of 5 MPa

软岩试件在试验过程中有如下规律和时效特征：（1）岩样在每一级应力加载瞬间，瞬时应变量随着应力水平的增加而增大，且总变形中瞬时应变占主要部分；（2）蠕变试验过程中，在较低的应力水平下，岩样的变形随时间的增长而增大，但减速蠕变现象不明显。应力水平随着时间增大时，逐渐呈现出等速蠕变现象，而蠕变速率呈增大趋势；（3）围压越大，相应的轴向变形量越小，岩样越不易产生轴向蠕变；（4）随着应力水平的进一步增大，岩样变形急剧增长，短时间内，随即破坏。

3.2 炭质页岩本构模型及本构方程的建立

由前述蠕变试验结果可知，低应力水平时，炭质页岩试件的变形由瞬时变形和不稳定蠕变变形两部分组成，其中不稳定蠕变变形经历了减速蠕变和等速蠕变。瞬时弹性变形要求蠕变模型里包括弹性元件，试验蠕变曲线反映了应变随时间增加而增大，则模型里应包括黏性元件。由于页岩岩样在低围压条件下，未出现明显的加速蠕变阶段，峰后页岩因塑性应变软化，强度急剧降低，为了描述软岩峰后蠕变变形破坏特性，引进一种塑性应变软化元件，简称 SS元件[17]。该元件基于 Mohr-Coulomb后继屈服准则，当应力σ未达到Mohr-Coulomb后继屈服应力σs时，SS元件的应变为0；当应力σ≥σs时，SS元件服从塑性应变软化流动规律。因此可以提出图所示的蠕变模型结构来描述页岩的蠕变力学特性。

图6 页岩黏蠕变力学模型结构Fig.6 Creep model structure of shale

模型分为两个部分：第I部分是典型的广义开尔文模型，用于描述页岩的瞬时弹性变形、减速蠕变变形和等速蠕变变形；第II部分为SS模型，用于描述页岩峰后的塑性应变软化特性。

在推导蠕变模型的本构方程之前，假定模型中的黏弹性和黏塑性应变率分量变形协调，则当σ＜σs时，模型简化为广义开尔文模型；当 σ≥σs，模型由广义开尔文模型与SS黏塑性元件串联组成。以下将推导该蠕变模型的本构方程。

（1）当σ＜σs时

广义开尔文模型由一个开尔文元件和一个弹簧串联组成，其本构方程的推导过程如下。

由于串联，

对式（5）进行进一步整理

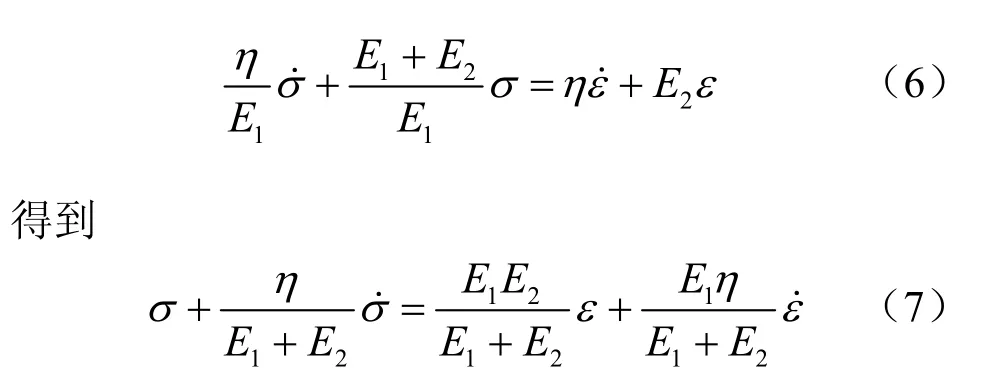
即模型的一维微分本构方程。式中：E1为瞬时弹性模型量；E2为黏弹性模型量；η为黏性系数；各符号上带点表示对该求导。

对式（8）进行0初始条件下的Laplace变换，则可得如下代数方程：

式中：pk、qk为决定材料性质的常数； sk为对时间的微分算子。

考虑线性黏弹性材料在突加载荷 σ=σ0H(t)作用下随时间而变换的应变响应，可表示为

式中：J(t)为蠕变柔量；H(t)为单位阶跃函数，可表示为

对式（12）进行Laplace变换，可得

再考虑对突加载荷σ=σ0H(t)进行Laplace变换，并注意到 L[H(t)]=1/s，则可得

将式（10）、（15）代入式（14），有

对一维情况下广义开尔文模型的微分本构方程式（7），有

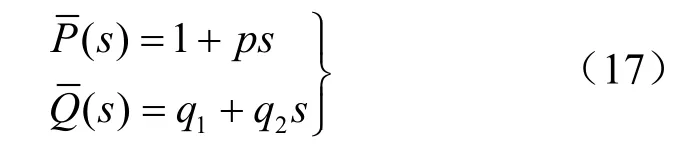
式中：

将式（17）代入式（16），得到广义开尔文模型蠕变柔量的象函数：

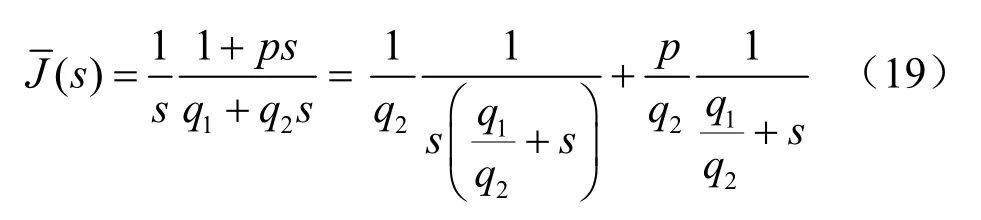
采用Heaviside展开式对式（19）进行Laplace逆变换，得到广义开尔文模型的蠕变柔量为

将式（18）代入式（20），整理可得

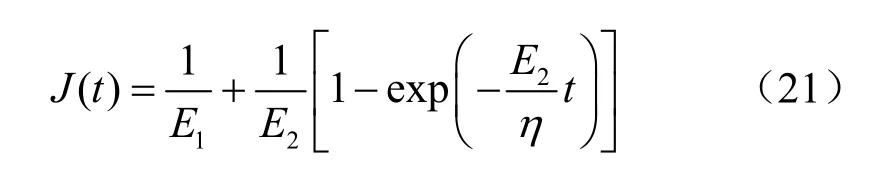
利用 Botzmann线性叠加原理，一维情况下的广义开尔文模型蠕变本构的方程的积分形式可以表示为

蠕变模型的三维本构模型可以由一维本构方程推广得到。在三维应力状态下，页岩内部的应力张量可分解为球应力张量σm和偏应力张量Sij，其表达式为

式中：δij为Kronecker函数。

一般地，球形张量σm只能改变材料的体积，而不能改变其形状，偏应力张量Sij只能引起形状变化而不引起体积的变化。同理，可以相应地将应变张量分解成球应变张量εm和偏应变张量eij，即

设页岩的剪切模型为G，体积变形模量为K，则对于三维应力状态下的虎克体有

耶格(Jaeger)与库克(Cook)给出了三维黏弹性本构关系[18]：

式中：P′、Q′与微分算子P、Q相似，但需将P、Q中的所有弹性模量、黏弹性模量换为弹性剪切模量和黏弹性剪切模量；黏滞系数换为剪切黏滞系数；P′′、Q′′为反映材料黏弹性体积变形的算子，若材料体积变形呈弹性，则可取Q′′=K，P′′=1(K为弹性体积模量)。

因此，在三维应力状态下广义开尔文模型的本构方程采用Stieltjes卷积分可以写成

式中：*为卷积符号。

在实验室三轴蠕变试验过程中，σ2=σ3，ε2=ε3，故

将式（30）代入式（29），积分得轴向应变：

式（31）为典型的广义开尔文模型的三维本构方程，K、G1、G2、ηG为模型的4个参数。

（2）当 σ≥σs时

模型由广义开尔文模型和 SS黏塑性模型串联组成，模型的总应变可认为由广义开尔文模型的应变与 SS模型的塑性应变之和，因此模型三维微分形式的本构方程为

对SS塑性模型，有

采用相关联流动准则时，塑性势函数g可取为塑性屈服函数 f，服从应变软化模型 Mohr-Coulomb后继屈服函数，即

4 炭质页岩蠕变模型参数辨识

根据蠕变试验曲线规律以及所建立的与试验曲线吻合的蠕变元件模型，采用数学方法，可对蠕变模型的参数进行辨识。由章节3可知，模型有4个参数：K、G1、G2、η，岩体在静水压力作用下其体积变形在受力瞬间完成，不随时间产生体积变化，而且蠕变过程中，岩体的泊松比μ保持不变[19]。

当t=0时，根据式（22）可求得

将所测试验数据代入式（35），求得E1= 1.96 GPa。根据现场实际的工程情况和单轴压缩室内试验结果，泊松比μ=0.37，进一步求得K = 2.5 GPa。因此，只需拟合G1、G2、η三个参数。

借助最小二乘法对两个参数进行非线性回归分析，运用 MATLAB编制回归分析程序，分别对荷载水平为σ1= 27.5、35.0、42.5、50.0、57.5 MPa等6个应力水平下的蠕变曲线进行模型参数辨识，结果如表1和图7所示。由图可见，试验曲线有一定的离散性，但模型的拟合曲线与试验曲线基本吻合，辨识参数的结果能够体现试验岩样的蠕变特征，可用于岩石蠕变的模拟分析。

表1 模型参数辨识结果Table1 Identification results of model parameters

5 结 论

(1) 三轴压缩条件下，围压较低时页岩试样呈现出明显的脆性破坏和应变软化特性。三向应力状态下，岩样受主应力作用，主平面为受压平面，试块产生剪切破坏。岩石的强度特性随着应力状态的改变而变化，相比单轴应力状态，三向应力状态下的岩石强度有所提高，主要体现在岩样的弹性模量、峰值强度和残余强度等参数。

(2) 在较低应力水平下，蠕变现象不明显，随着应力水平的增大，蠕变现象逐渐明显。在更高的应力水平下，试件并未出现加速蠕变的情况，从变形加剧直至溃屈，历时很短。岩样在每一级应力加载瞬间，瞬时应变量随着应力水平的增加而增大，且总变形中，瞬时应变占主要部分。围压越大，相应的轴向变形量越小，岩样越不易产生轴向蠕变，在本试验提供的围压下，只出现了减速蠕变和等速蠕变阶段。

依据页岩试样的三轴压缩蠕变试验曲线，建立了依托工程岩石蠕变全过程的黏弹塑性应变软化蠕变模型，并推导了蠕变模型的一维和三维本构方程，确定了该模型的参数，并在此基础上，借助MATLAB程序中的最小二乘法工具，对模型的参数进行了辨识，拟合曲线与试验曲线基本吻合，结果表明所建模型能够描述页岩三轴压缩条件下的蠕变特征，可以用来研究该隧道软弱破碎围岩的蠕变性质和稳定性。

图7 模型参数辨识的最小二乘拟合曲线Fig.7 Fitting curves by least-squares procedure of parameters identification

[1]刘建忠,杨春和,李晓红,等. 万开高速公路穿越煤系地层的隧道围岩蠕变特性试验研究[J]. 岩石力学与工程学报,2004,23(22): 3794－3798.LIU Jian-zhong,YANG Chun-he,LI Xiao-hong,et al.Testing study on creep of coal rocks in the tunnel of Wan-Kai speedway[J]. Chinese Journal of Rock Mechanics and Engineering,2004,23(22): 3794－3798.

[2]刘钦,李术才,李利平,等. 软弱破碎围岩隧道大变形施工力学行为及支护对策研究[J]. 山东大学学报（工学版）,2011,41(3): 118－125.LIU Qin,LI Shu-cai,LI Li-ping,et al. Study on large deformation construction mechanical behavior and support measures of soft rock in deep buried extra long tunnel[J]. Journal of Shandong University (Engineering Science),2011,41(3): 118－125.

[3]YAMAGUCHI U,SHIMOTANI T. A case study of slope failure in a limestone quarry[J]. Int. J. Rock Mech. Min.Sci. & Geomech. Abstr.,1985,23(1): 95－104.

[4]SINGH A,MITCHELL J K. General stress-strain-time function for clay[J]. Journal of the Clay Mechanics and Foundation Division,ASCE,1968,94(SM1): 21－46.

[5]MESRI G,REBRES-CORDERO E,SHIELDS D R,et al. Shear stress-strain-time behavior of clays[J].Geotechnique,1981,31(4): 537－552.

[6]张治亮,徐卫亚,王伟. 向家坝水电站坝基挤压带岩石三轴蠕变试验及非线性黏弹性蠕变模型研究[J]. 岩石力学与工程学报,2011,30(1): 132－140.ZHANG Zhi-liang,XU Wei-ya,WANG Wei. Study of triaxial creep tests and its nonlinear visco-elastoplastic creep model of rock from compressive zone of dam foundation in Xiangjiaba hydropower station[J]. Chinese Journal of Rock Mechanics and Engineering,2011,30(1): 132－140.

[7]杨春和,陈锋,曾义金. 盐岩蠕变损伤关系研究[J]. 岩石力学与工程学报,2002,21(11): 1602－1604.YANG Chun-he,CHEN Feng,ZENG Yi-jin.Investigation on creep damage constitutive theory of salt rock[J]. Chinese Journal of Rock Mechanics and Engineering,2002,21(11): 1602－1604.

[8]卢萍珍,曾静,盛谦. 软黏土蠕变试验及其经验模型研究[J]. 岩土力学,2008,29(4): 1041－1044.LU Ping-zhen,ZENG Jing,SHENG Qian. Creep tests on soft clay and its empirical models[J]. Rock and Soil Mechanics,2008,29(4): 1041－1044.

[9]刘钦. 炭质页岩隧道软弱破碎围岩大变形机理与控制对策及其应用研究[博士学位论文D]. 济南: 山东大学,2011.

[10]水利规划设计总院. GB/T50266－99 工程岩体试验方法标准[S]. 北京: 中国计划出版社,1999.

[11]李荣,孟英峰,罗勇,等. 泥页岩三轴蠕变实验及结果应用[J]. 西南石油大学学报,2007,29(3): 57－59.LI Rong,MENG Ying-feng,LUO Yong,et al. Triaxial creep test of mudstone and the result application[J].Journal of Southwest Petroleum University,2007,29(3): 57－59.

[12]任松,姜德义,杨春和,等. 共和隧道开裂段页岩蠕变本构试验及离散元数值模拟研究[J]. 岩土力学,2010,31(2): 416－421.REN Song,JIANG De-yi,YANG Chun-he,et al. Creep tests on shale of cracking position in Gonghe tunnel and simulating it by DEM[J]. Rock and Soil Mechanics,2010,31(2): 416－421.

[13]沈荣喜,刘长武,刘晓斐. 压力水作用下炭质页岩三轴蠕变特征及模型研究[J]. 岩土工程学报,2010,32(7):1031－1034.SHEN Rong-xi,LIU Chang-wu,LIU Xiao-fei. Triaxial rheology characteristics and model of carbonaceous shale in pressure water[J]. Chinese Journal of Geotechnical Engineering,2010,32(7): 1031－1034.

[14]何沛田,黄志鹏,邬爱清. 确定软岩岩体承载能力方法研究[J]. 地下空间,2004,24(1): 89－93.HE Pei-tian,HUANG Zhi-peng,WU Ai-qing. Study on Estimation of bearing capacity of soft rock body[J].Underground Space,2004,24(1): 89-93.

[15]周德培,朱本珍,毛坚强. 蠕变力学原理及其在岩土工程中的应用[M]. 成都: 西南交通大学出版社,1995.

[16]高延法,范庆忠,崔希海,等. 岩石蠕变及其扰动效应试验研究[M]. 北京: 科学出版社,2007.

[17]杨峰. 高地应力软岩巷道变形破坏特征及让压支护机理研究[博士学位论文D]. 徐州: 中国矿业大学,2009.

[18]耶格 J C,库克 N G W. 岩石力学基础[M]. 中国科学院工程力学研究所译. 北京: 科学出版社,1983.

[19]孙钧. 岩土材料蠕变及其工程应用[M]. 北京: 中国建筑工业出版社,1999.