基于自适应反演滑模的末制导律设计

舒燕军, 唐硕

(西北工业大学 航天学院, 陕西 西安 710072)

基于自适应反演滑模的末制导律设计

舒燕军, 唐硕

(西北工业大学 航天学院, 陕西 西安 710072)

针对三维导弹-目标相对运动模型,结合反演控制、滑模控制和自适应技术,设计了一种新的自适应反演滑模末制导律。针对目标机动加速度上界难以获取的问题,将目标机动加速度视作模型的干扰,设计了一种自适应律对其进行在线估计,并将估计值补偿到制导律中。运用李亚普诺夫稳定性理论证明了系统的全局渐进稳定性和误差的收敛性。仿真结果证明了所设计的自适应反演滑模末制导律对机动目标的鲁棒性和有效性。

反演控制; 滑模末制导律; 自适应; 李亚普诺夫稳定性

引言

目前,传统的比例制导律及其各种改进形式广泛应用于导弹制导系统中,比例制导的弱点是不能对目标机动进行有效的补偿,在对付高速大机动来袭目标时往往不能奏效。因此各种基于现代控制理论的现代制导律正成为目前研究的焦点[1]。

反演控制基于李亚普诺夫稳定性理论,从系统的第一个状态子系统开始,通过从外向内逐步递推设计来推导整个系统的控制律。反演控制是解决非线性系统控制问题的有效手段,因此在导弹制导控制中得到了广泛的应用[6]。

如果将滑模控制与反演控制相结合,可以增加系统对不确定性的鲁棒性,又可以简化反演控制的设计。本文将反演控制和滑模控制方法相结合,将目标机动加速度视作制导模型的干扰,基于李亚普诺夫稳定性理论设计了一种自适应律对其进行在线估计,同时证明了系统的全局渐进稳定性和误差的收敛性,设计了一种对目标机动具有鲁棒性的自适应反演滑模末制导律。

1 三维末制导问题的数学模型

为了研究末制导律,选取某一时间区间Δt起始时刻的视线坐标系Ox3y3z3作为末制导过程的参考坐标系(见图1),其原点O位于导弹的质心,x3轴与视线重合,指向目标为正,y3轴位于铅垂面内与x3轴垂直,指向上方为正,z3轴方向按右手定则确定。易知z3轴位于水平面内。

(1)

(2)

其中:

(3)

(4)

其中:

将u=aMy3作为系统输入,目标机动d=aTy3作为系统干扰。在实际的末制导过程中,由于目标的高速机动和各种外界随机干扰,制导模型存在不确定性,需要对各种不确定因素具备良好鲁棒性的制导律才能保证拦截效果。

2 自适应反演滑模末制导律设计

2.1 反演滑模末制导律设计

步骤1:取z1=x1,定义稳定项:

α1=cz1

(5)

式中,c=const>0。构造Lyapunov函数:

(6)

(7)

对式(6)求导得:

(8)

步骤2:设计线性滑模面:

s=k1z1+z2

(9)

式中,k1=const>0。构造Lyapunov函数:

(10)

则有:

(11)

设计如下制导律:

(12)

将式(12)带入式(11)得:

(13)

取系数矩阵:

则有:

(14)

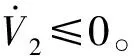
2.2 自适应反演滑模末制导律设计

(15)

构造Lyapunov函数:

(16)

则有:

(17)

进一步设计如下制导律:

(18)

式中,h,β=const>0。

将式(18)代入式(17)可得:

=-ZTQZ-hβ|s|

(19)

为了削弱滑模控制的抖振现象,进一步采用饱和非线性函数s/(|s|+δ)代替符号函数sgn(s),则最终的自适应反演滑模制导律可写为:

(20)

3 仿真分析

为了检验本文提出的自适应反演滑模末制导律的有效性,下面对其进行仿真验证,并与传统广义比例制导律进行对比分析。广义比例制导律(PN)[7]为:

(21)

式中,导航比系数k=4.0。

数字仿真结果表明,自适应反演滑模制导律的脱靶量为0.37 m, 广义比例制导律的脱靶量为28.51 m。分析仿真结果可知,本文设计的自适应反演滑模末制导律对目标机动具有较好的鲁棒性,且制导精度优于传统的广义比例制导。

图2 PN制导律下控制量曲线

图3 PN制导律下视线角速率曲线

图4 自适应反演滑模制导律下视线角增量曲线

图5 自适应反演滑模制导律下视线角速率曲线

图6 自适应反演控制量曲线

4 结束语

针对三维目标拦截问题,本文结合反演控制、自适应技术和滑模控制方法,设计了一种新的自适应反演滑模末制导律。将目标机动加速度视作系统的干扰项,基于李亚普诺夫稳定性理论设计了自适应律对干扰进行在线估计,证明了系统全局渐进稳定和误差最终一致有界。而且本文设计的自适应反演滑模末制导律不需要太多的观测信息,计算量较小,易于工程实现。

[1] 周荻.寻的导弹新型导引规律[M].北京:国防工业出版社,2002.

[2] 王洪强,方洋旺,伍友利.滑模变结构控制在导弹制导中的应用综述[J].飞行力学,2009,27(2):11-15.

[3] 顾文锦,赵红超,杨智勇.变结构控制在导弹制导中的应用综述[J].飞行力学,2005,23(1):1-4.

[4] Brierley S D, Longchamp R. Application of sliding mode control to air-air interception problem [J]. IEEE Transactions on Aerospace and Electronic Systems, 1990, 26(2):306-325.

[5] Babu K R, Sarmah J G, Swamy K N. Switched bias proportional navigation for homing guidance against highly maneuvering target[J]. Journal of Guidance,Control,and Dynamics,1994,17(6):1357-1363.

[6] 张友安,胡云安.导弹控制和制导的非线性设计方法[M].北京:国防工业出版社,2003.

[7] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2006.

Guidancelawdesignbasedonadaptivebacksteppingslidingmodecontrol

SHU Yan-jun, TANG Shuo

(College of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China)

Based on backstepping design,adaptive control and sliding mode control,a new adaptive backstepping sliding mode controller was designed for the case of a three-dimensional interception. To confirm the upper bound of uncertainties in sliding-mode control system,considering the maneuvering acceleration of targets as a disturbance. An adaptive law was designed to estimate the value of upper bound in real-time,and its stability and error convergence were testified based on the Lyapunov theorem. Simulation results show that the adaptive backstepping sliding mode law is effective.

backstepping control; sliding mode terminal guidance law; adaptive; Lyapunov stability

2011-06-10;

2011-11-24

舒燕军(1985-)，男，江苏宿迁人，博士研究生，研究方向为飞行器制导与控制、建模与仿真；

唐硕(1963-)，男，四川达州人，教授，博士生导师，研究方向为飞行器动力学与控制等。

TJ765

A

1002-0853(2012)02-0163-04

(编辑：王育林)