带动力机动弹头制导方法研究
孟 京
(西北工业大学 航天学院, 陕西 西安 710072)
带动力机动弹头制导方法研究
孟 京
(西北工业大学 航天学院, 陕西 西安 710072)
为解决一种带动力机动弹头的制导问题,给出了弹头在下降拉平段、平飞段、攻击段的制导方法。在下降拉平段,采用程序转弯下降与基于几何法的按圆弧拉平制导律结合的方法,使终端精确达到平飞段所需的高度。在平飞段分别给出了高度保持以及侧向转弯过航路点的制导律,以提高制导探测精度并避开威胁区域。攻击段在基本制导律设计基础上给出了多种攻击方式。各制导方法均通过三自由度弹道仿真得到验证,具有较强的工程实用性。
机动弹头; 制导; 航路点; 几何法; 攻击方式
引言
随着各种反导武器的不断发展,对弹道导弹的突防能力提出了越来越高的要求。传统弹道导弹的弹头再入大气层后采用无控飞行,故又称作惯性弹头,其飞行弹道主要取决于与弹体分离点的位置、速度大小和弹道倾角。扣除飞行过程中干扰的作用,惯性弹头分离后的弹道是确定的,较容易被反导导弹拦截。
机动弹头与弹体分离后可根据需要改变飞行弹道。为了提高突防能力,美国从20世纪60年代初开始发展机动弹头。截止目前,对于机动弹头制导问题国内外做了大量的研究,包括躲避机动方式、速度控制[1]、高精度制导[2]等方法。通过改变飞行弹道来躲避敌方拦截的机动弹头称为躲避型机动弹头。不但改变飞行弹道,而且通过末制导装置来提高命中精度的机动弹头称为精确型机动弹头或高级机动弹头。精确型机动弹头中,美国“潘兴”Ⅱ导弹为最典型的代表[3]。
上述研究的机动弹头均不带动力,并且弹道形式比较单一。考虑一种具有面对称大升阻比构型的带动力机动弹头,其本身携带速度补偿发动机,用于增强中段的机动能力并增加航程,弹道形式明显区别于传统机动弹头。本文针对此种机动弹头的再入飞行及攻击制导问题展开研究。
1 机动弹头数学模型
1.1 飞行阶段的划分
将带动力机动弹头的再入机动飞行攻击目标的过程分为三段,如图1所示。
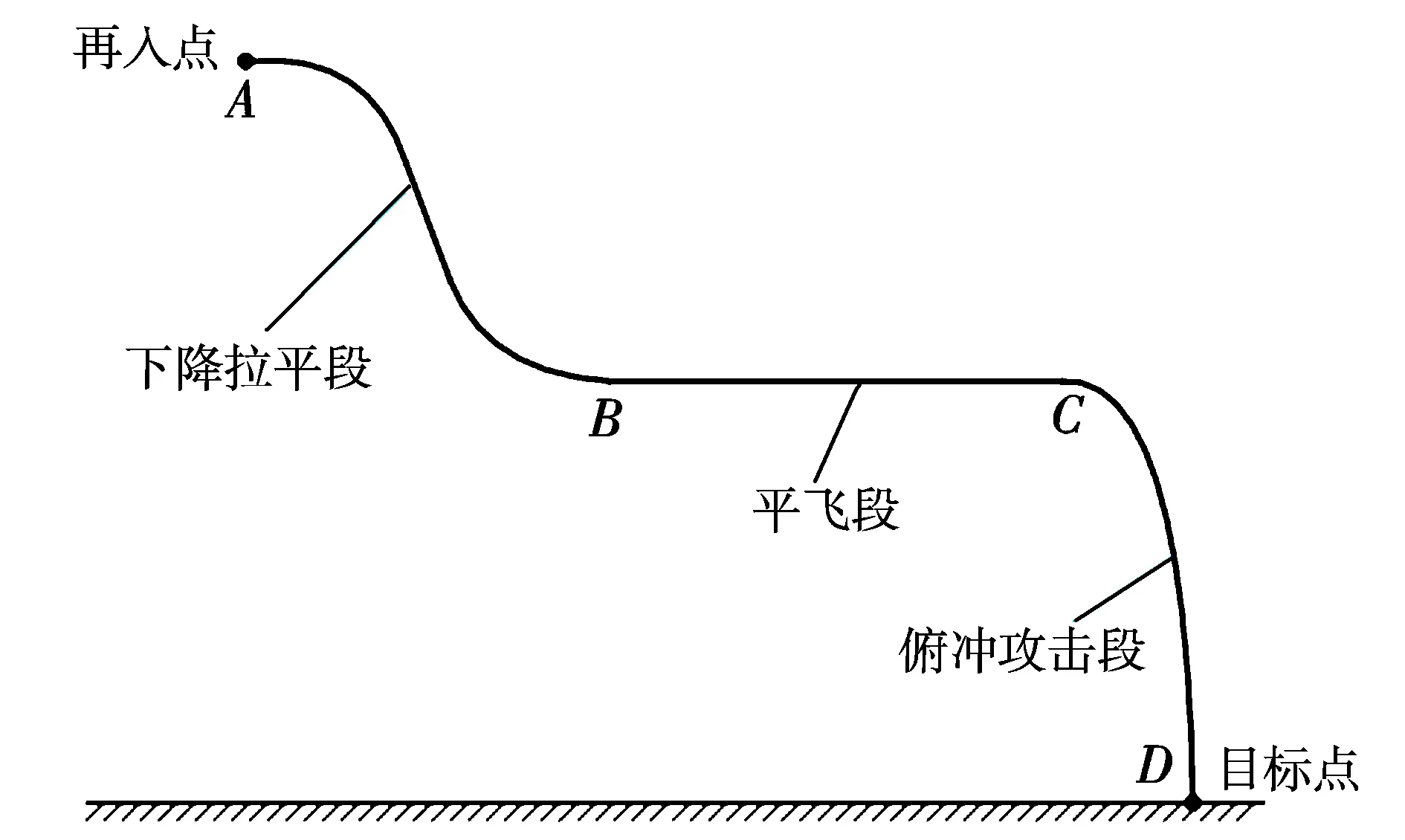
图1 带动力机动弹头再入飞行阶段划分
第一段:下降拉平段(AB段)。在此段内,起始时刻机动弹头转弯快速降低飞行高度,在该段的终端对弹道进行拉平,以转入平飞状态。该段的主要要求为终端拉平的高度要精确满足设定值。
第二段:平飞段(BC段)。在此段内,机动弹头保持在固定高度飞行,这是为了提高制导探测设备精度。此外,机动弹头在此段要通过侧向转弯对威胁区域进行规避,以增强突防效果。
第三段:俯冲攻击段(CD段)。此段的目标是控制机动弹头俯冲,使机动弹头以特定的攻击方式攻击目标。
1.2 运动方程
机动弹头为大升阻比构型,采用倾侧转弯方式,故假设侧滑角为零,控制参数为攻角和倾侧角。为了便于制导律设计,在机动弹头飞行的不同阶段制导采用不同形式的运动方程。在下降拉平段制导律设计时将运动限定在纵平面内,设地球为不旋转的均质圆球,建立平面再入坐标系中的质心运动方程[4]。由于机动弹头在平飞段要进行侧向转弯,故在研究机动弹头平飞段制导时,采用平面大地假设下的飞行器运动方程:
(1)
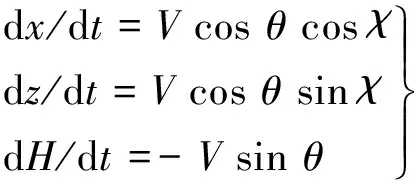
(2)
式中,V为飞行速度;χ为航迹偏角;θ为速度倾角;X,Y分别为气动阻力和升力;g为地球引力加速度;Pc为速度补偿发动机推力大小;k为发动机开关标识,取值为0或1;x,z为平面地理坐标系中水平面内位置;H为飞行高度;m为弹头质量;控制量为攻角α和倾侧角υ。
下降拉平段制导采用文献[5]中按程序转弯下降,以及按圆弧拉平的方法。本文着重解决平飞段及攻击段的制导问题。
2 平飞段制导
平飞段首先要进行飞行高度保持,使飞行高度恒定,并且通过发动机的开关机对损失的速度进行补偿。本文在文献[5]对纵平面平飞状态保持制导方法的基础上,进一步研究侧向转弯规避威胁区域制导问题。
倾侧转弯的目的是为了避开威胁区域。本文假定已经由规划算法给出了一系列航路点,只要经过这些航路点即可确保避开威胁区域,问题即归结为逐个经过每个航路点的制导问题。对于此问题,导引法是一种基本思路,即每一时刻均把下一个要通过的航路点作为虚拟目标,通过比例导引的方式给出制导指令,然而导引法要求视线距离变化率小于0才可应用,故可靠性不够。
本文采用几何法设计过航路点制导律,基本思想为:首先建立转弯半径与动力学模型之间的联系,进而根据航路点位置确定转弯半径,最终由解析关系式解算出制导指令。
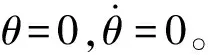
(3)
由式(3)中的运动方程可得转弯半径:
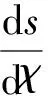
(4)
转弯半径也可采用如下几何方法计算得出。如图2所示,在平面地理坐标系xOz平面,设当前飞行器位置为(x1,z1),速度为(Vx,Vz),下一个航路点位置为(x2,z2)。记两点间直线距离为d12,则转弯半径可表示为:
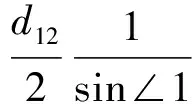
(5)
从而,可求得当前转弯倾侧角:
υ=arctan(V2/gR)
(6)
可见,平飞条件下,转弯倾侧角表达式与发动机推力、攻角均无关。
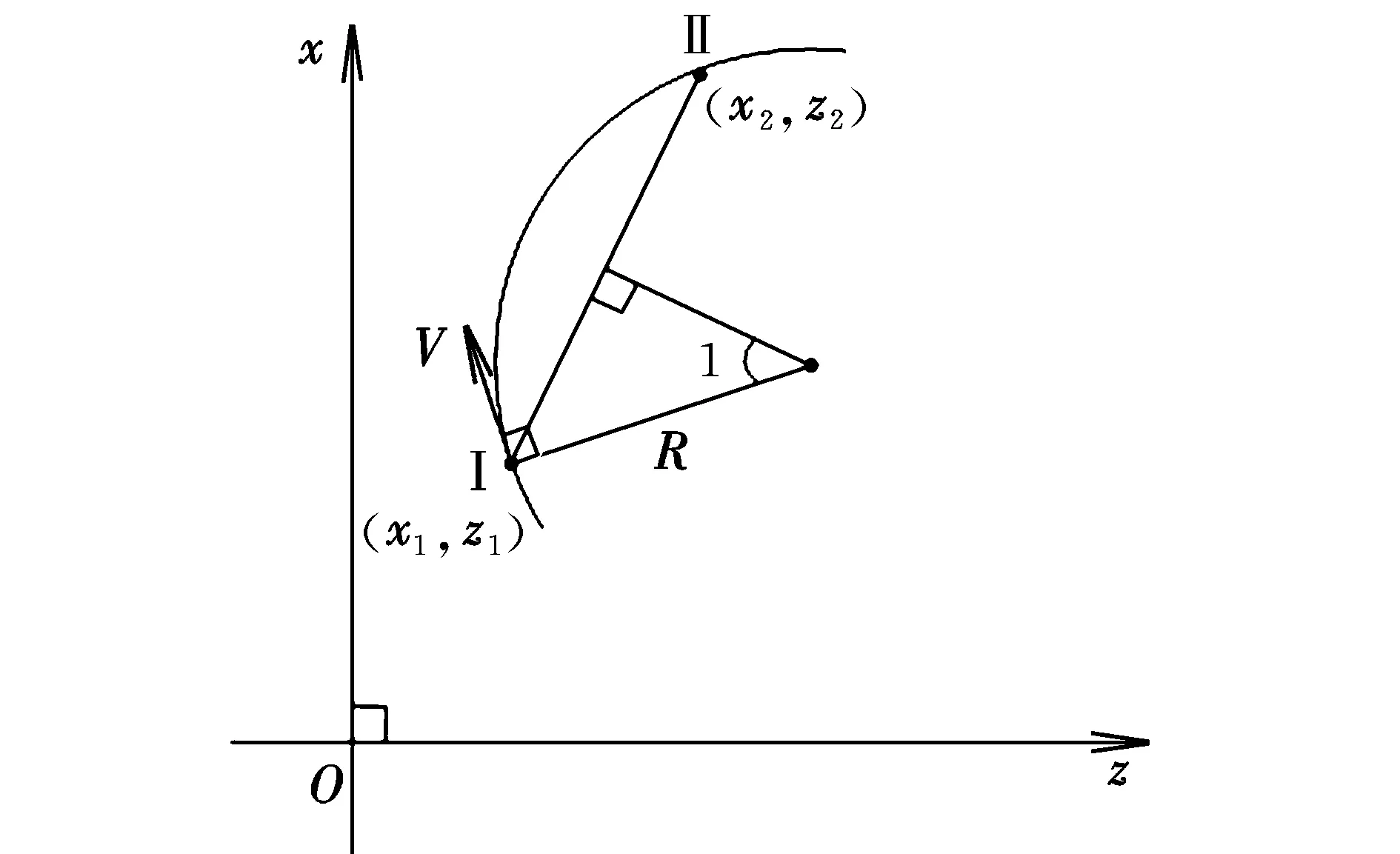
图2 平飞段倾侧转弯半径计算示意图
攻角计算需讨论两种情况。发动机关闭时升力系数CL(Ma,α)用下式计算:
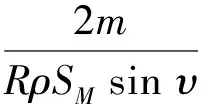
(7)
式中,Ma为马赫数;SM为弹头参考面积。当发动机开启时,记:
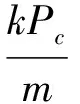
(8)
则有下式成立:
(9)
根据式(7)和式(9),采用迭代法并根据气动参数插值可获得所需攻角α。
实际计算中,在每一个制导周期内根据当前飞行状态和下一个航路点位置可实时计算出当前所需攻角及倾侧角。
3 俯冲攻击段制导
3.1 制导律设计
为了实现对落角进行控制,采用变形比例导引,基本形式为[4]:
(10)
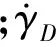
获得所需速度方向转率后,可近似地转化为需用过载的形式:
(11)
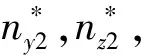
(12)
攻角α可由下式通过对气动参数插值求得:
(13)
倾侧角为:
(14)
3.2 多种攻击方式的实现
为了保证攻击效果,一方面对机动弹头终端的速度大小存在要求,另外对速度方向也存在要求。为了打击不同的目标,分别采用相应的多种攻击方式,如图3所示。
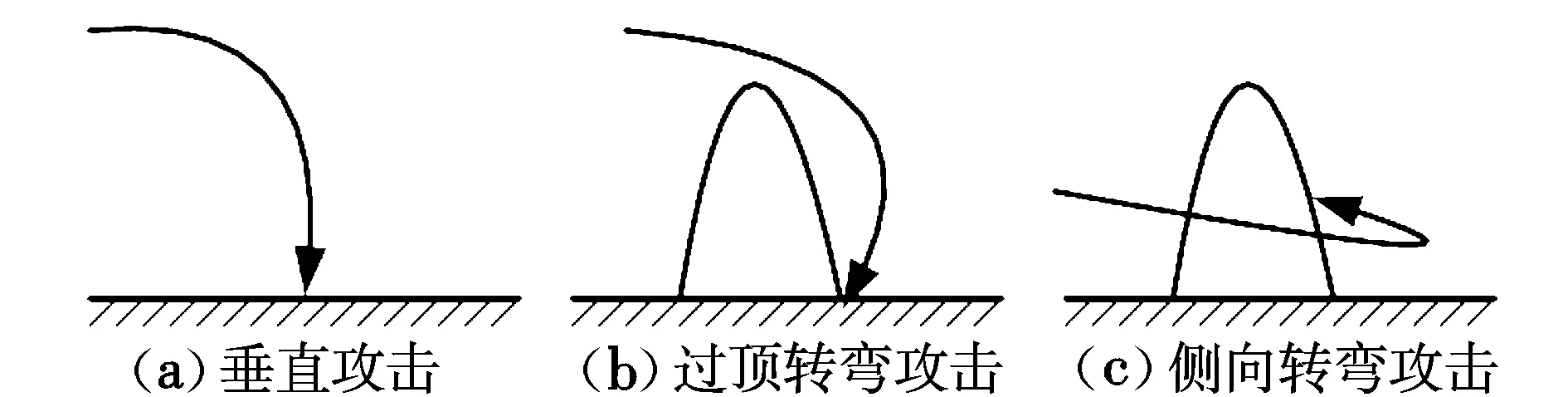
图3 多种攻击方式
(1)垂直攻击
在前面所讨论包含速度方向和速度大小控制导引规律基础上,设终端速度倾角γDF=-90°即可。
(2)过顶转弯攻击
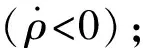
(15)
控制弹头转到对准虚拟点时转入纵平面内转弯攻击,则可实现所需方位角。
(3)侧向转弯攻击
实现方法:通过在目标后方同一高度设置一系列虚拟拐点,平飞过点转弯,转过来后采用变形比例导引垂直、倾斜或者水平攻击。虚拟拐点设置方法如图4所示,考虑到攻击段飞行距离很短,采用平面大地假设,根据平飞最后一个拐点及目标点在水平面内的相对位置,近似确定两个等边三角形,平飞最后一个拐点作为前面等边三角形的一个顶点,目标点不妨取为前面等边三角形的重心,相应地后面的等边三角形可以确定,后面三角形的三个顶点即作为在目标后方上空所设的虚拟拐点。对于速度过大或过小情况,等边三角形可用等腰三角形代替,并且大小可以调整。
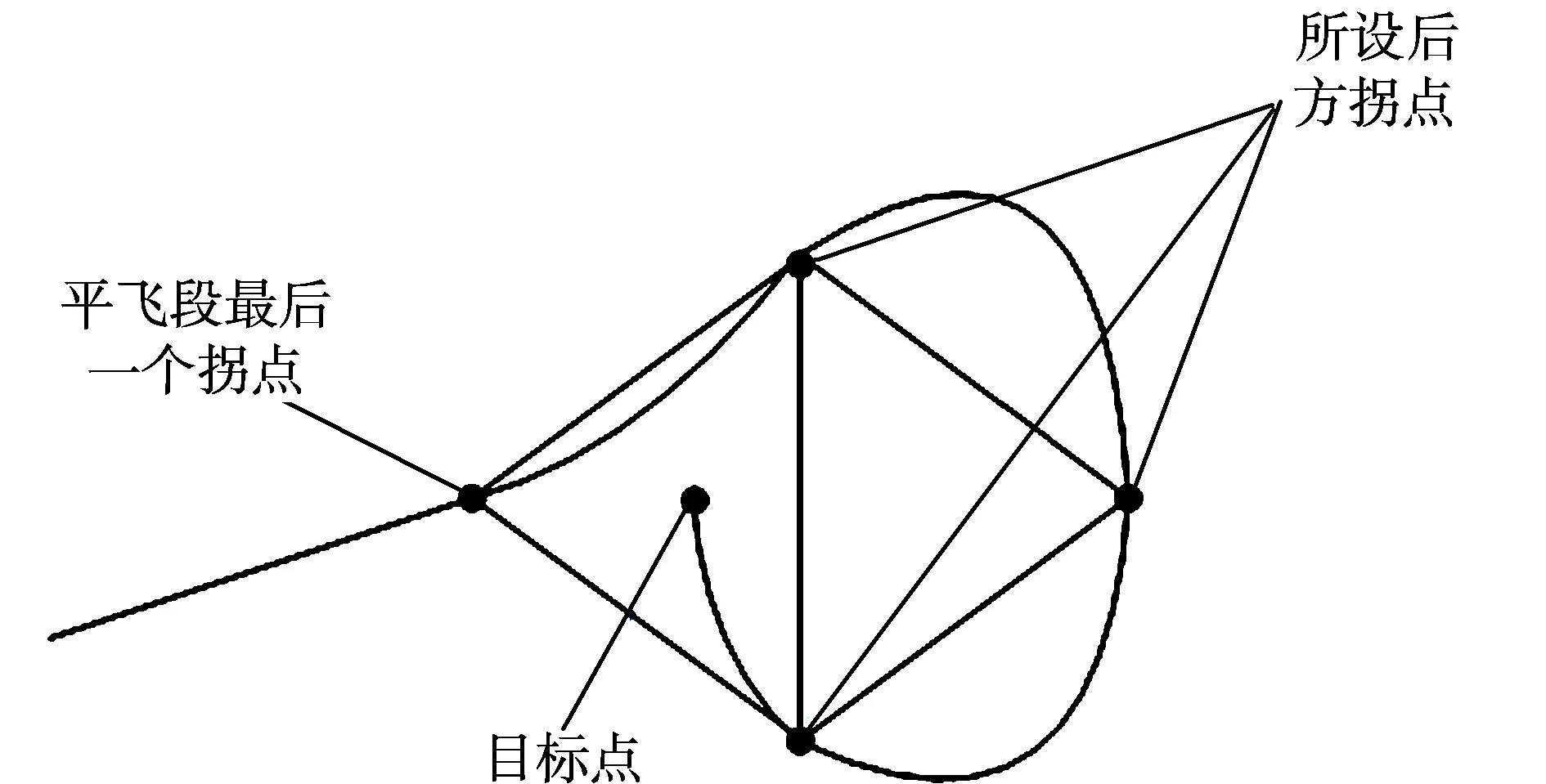
图4 侧向转弯攻击虚拟拐点设置示意图
4 制导实例仿真
采用文献[3]中设定的带动力机动弹头总体及气动参数,对包括下降拉平段、平飞段、攻击段的完整制导过程进行了三自由度弹道仿真。仿真中考虑大气密度扰动为±15%,升力系数、阻力系数扰动为±10%。在平飞段设定相应的航路点以避开拦截区域,在攻击段考虑多种攻击方式。
图5、图6分别给出了平飞段按导引法过航路点和按本文给出的几何法过航路点的制导效果。可以看出,导引法能够顺利经过前3个航路点,但是向第4个航路点导引时由于出现了视线距离大于0的情况,故导致发散,无法经过航路点;而本文给出的几何法则没有此限制,能够顺利经过所有航路点。
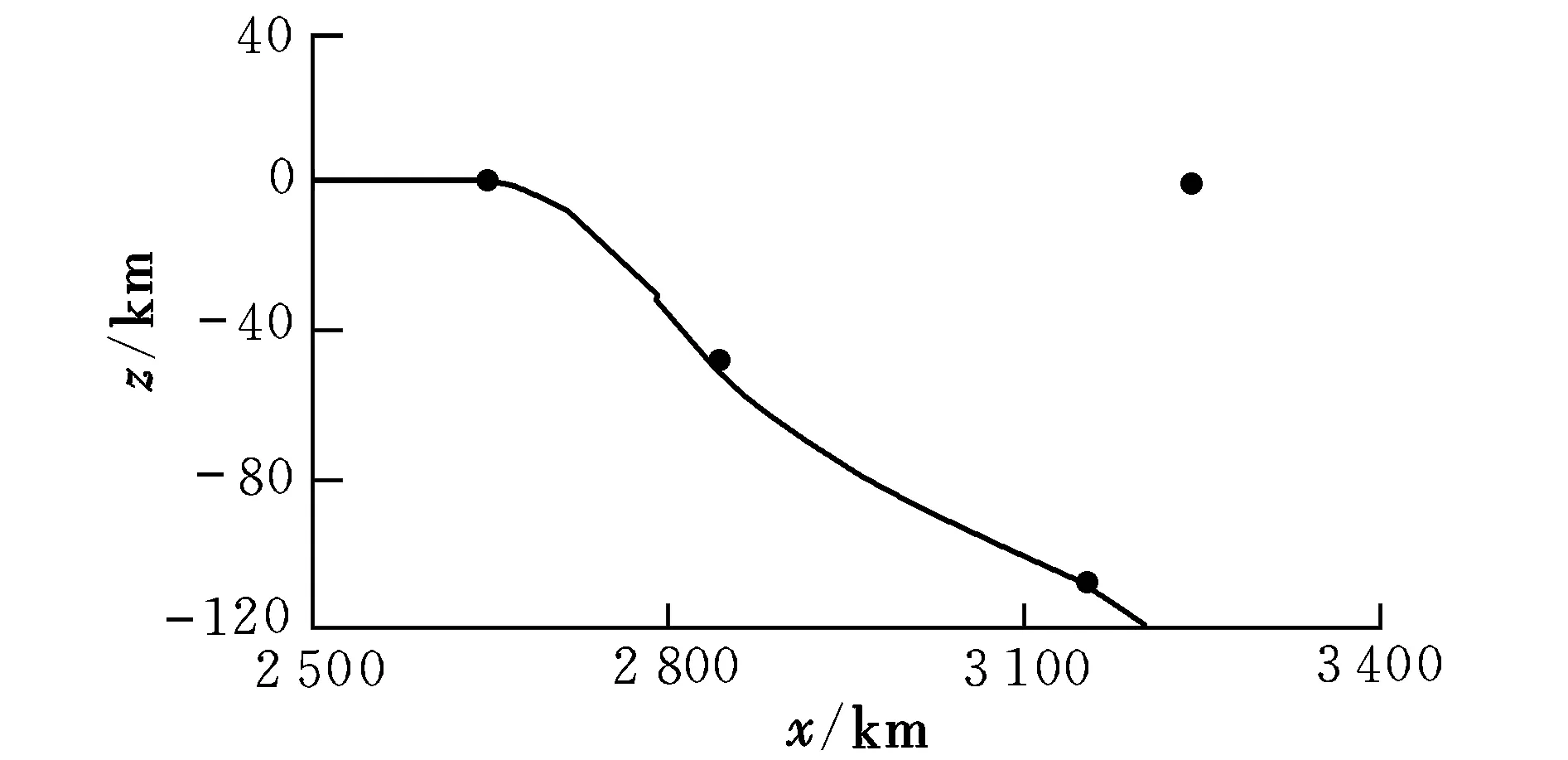
图5 平飞段侧向转弯过航路点(导引法)
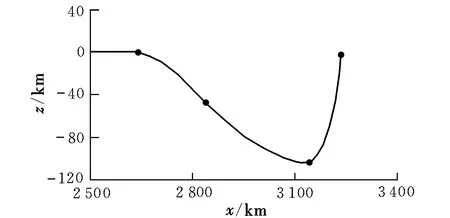
图6 平飞段侧向转弯过航路点(几何法)
图7给出了垂直攻击方式下平飞与攻击段的三维弹道曲线(λs为经度,φs为纬度),可以看出平飞段一直保持在设定的平飞高度,并且顺利通过了每一个设定的航路点,最终以垂直方向命中目标,终端落角为89.6°,脱靶量小于5 m,满足制导任务要求。
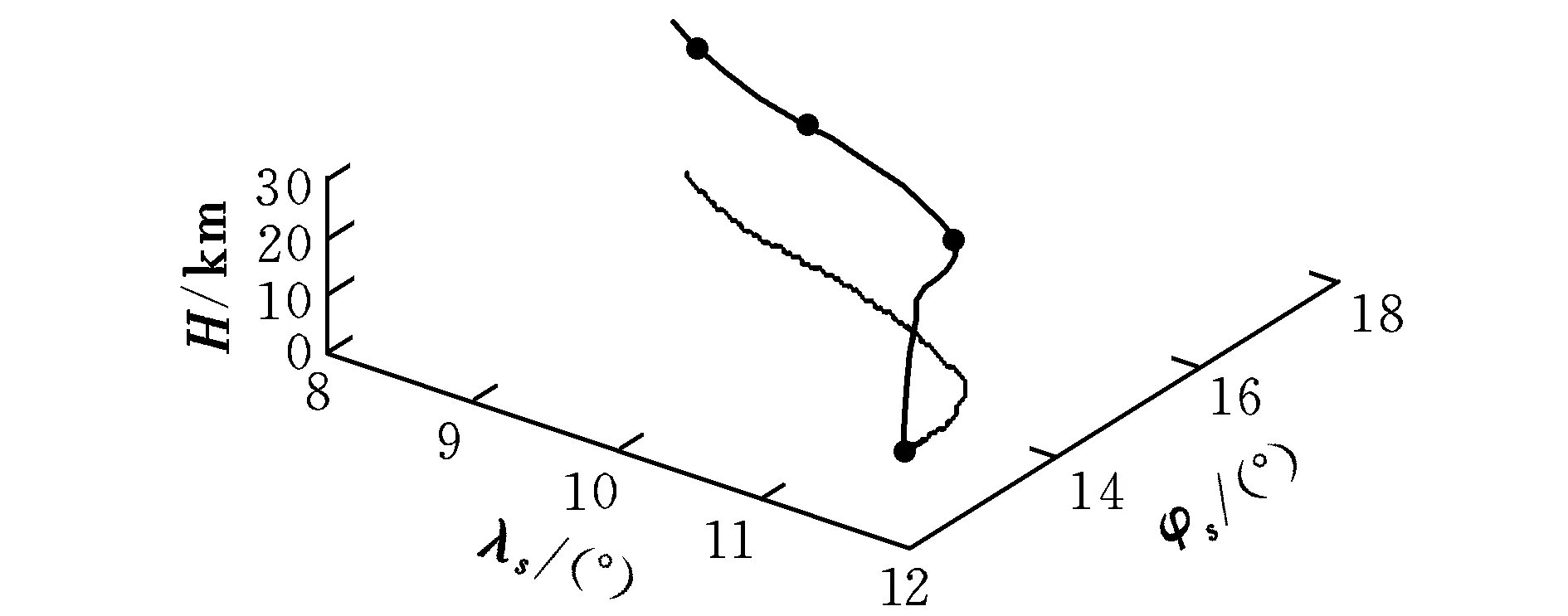
图7 平飞与攻击段三维弹道曲线(垂直攻击)
图8给出了过顶转弯攻击方式下高度随射程变化曲线,可清晰看出过顶转弯攻击目标的过程,落角为-29.8°,十分接近设定的落角要求-30°,终端脱靶量小于5 m。
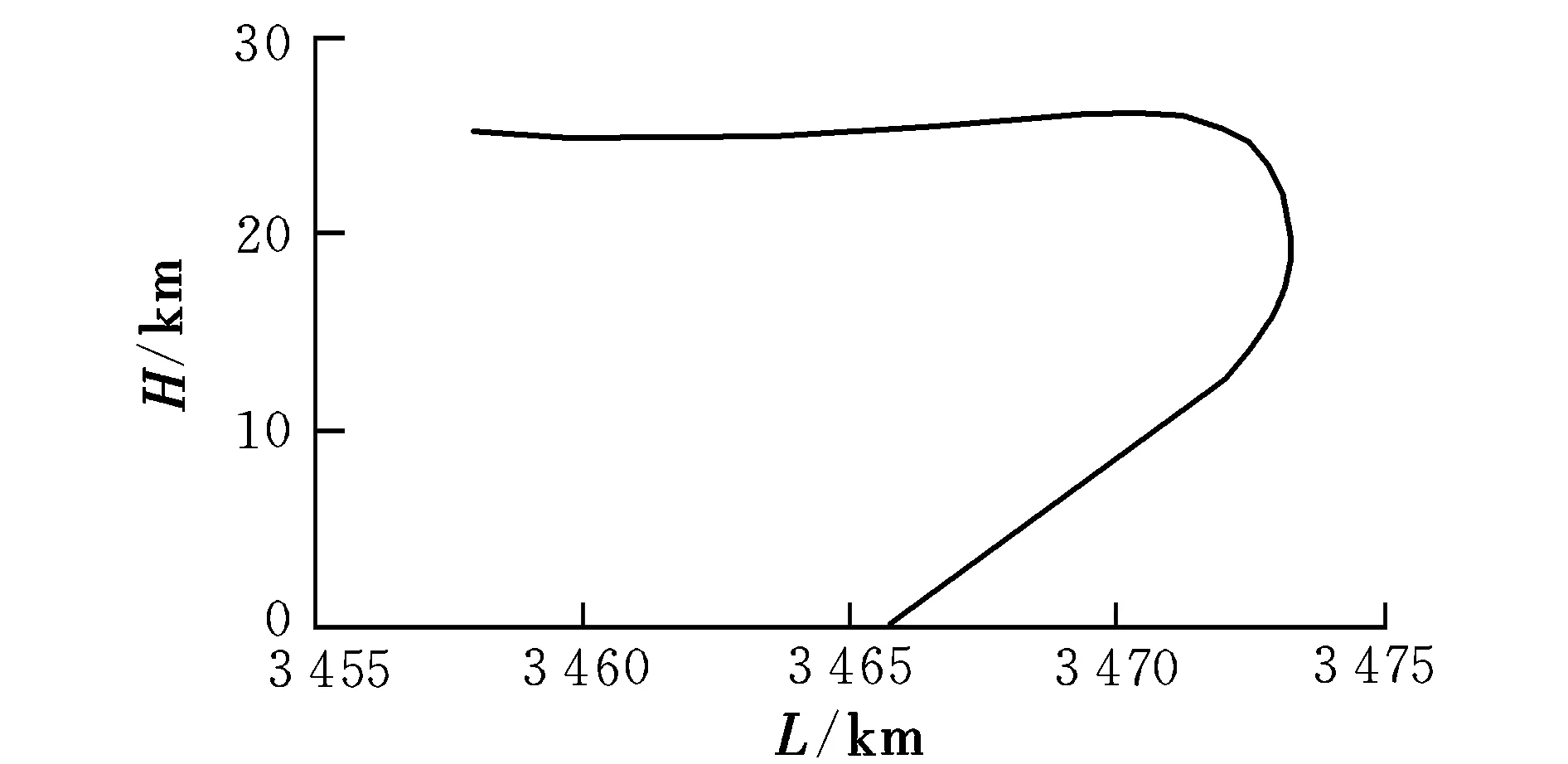
图8 攻击段高度-射程曲线(过顶转弯攻击)
图9、图10分别给出了侧向转弯攻击方式下整个飞行过程的经度-纬度变化曲线及三维弹道曲线。从图9的经纬度变化曲线可以看出,在侧向转弯攻击段可以顺利通过根据等边三角形设定的拐点。从图10的三维弹道曲线可以清晰看出下降拉平段、平飞段、侧向转弯攻击段的完整过程,侧向转弯经过所有拐点后俯冲攻击目标,终端脱靶量小于5 m。
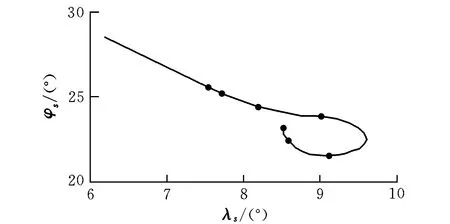
图9 完整的纬度-经度曲线(侧向转弯攻击)
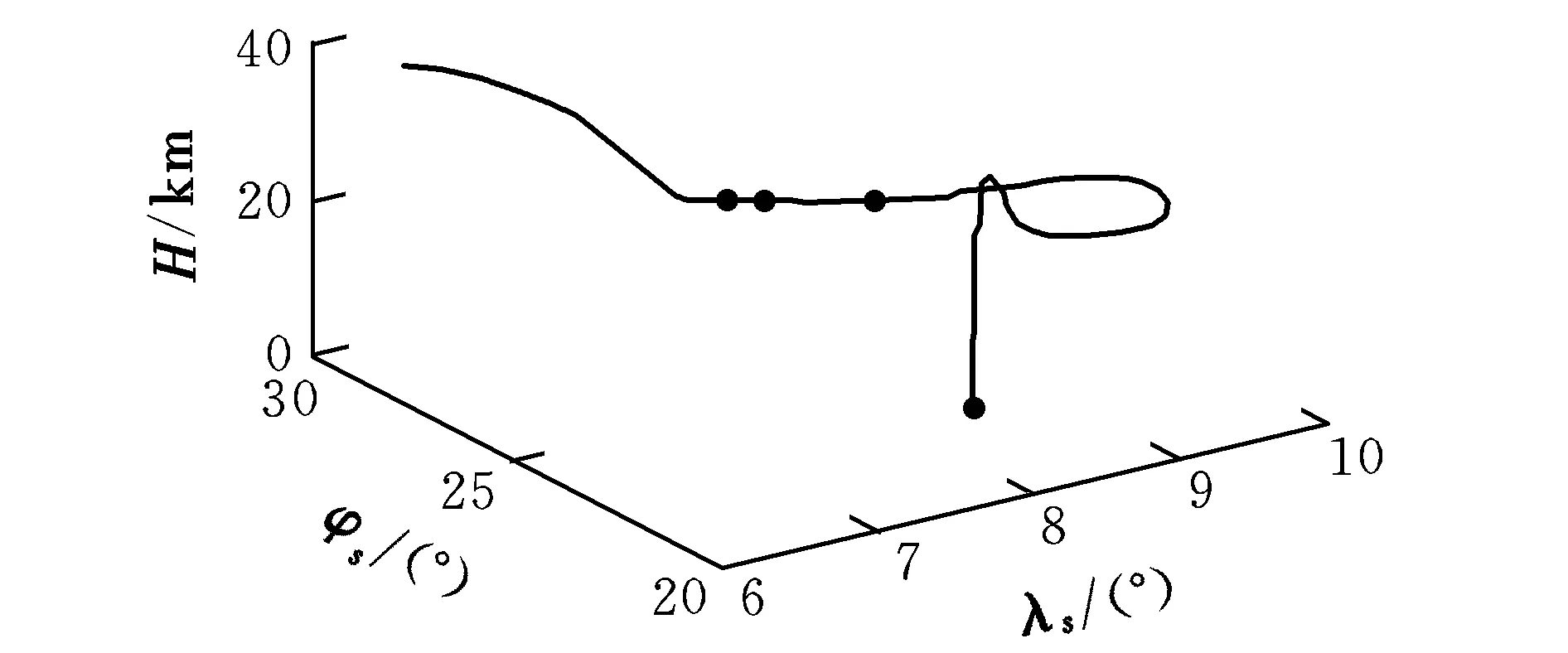
图10 完整的三维弹道曲线(侧向转弯攻击)
以上仿真结果表明,下降拉平段、平飞段、攻击段的各制导方法均得到了很好检验,能够满足带动力机动弹头的特殊制导任务要求。
5 结束语
本文较完整地给出了带动力机动弹头在下降拉平段、平飞段、攻击段等各个飞行阶段的制导方法,获得了较好的制导效果。平飞段给出的侧向转弯过航路点制导方法,具有便于应用、可靠性高的特点。该设计思想基于考虑动力学模型的几何法,获得的解析公式为制导方法的工程应用提供了极大便利。攻击段充分利用现有制导方法的优化组合,在不增加制导律复杂性的同时,实现了各种特定的攻击方式。
[1] 赵汉元,陈克俊.再入机动弹头的速度控制[J].国防科学技术大学学报,1993,15(2):11-17.
[2] 王洪强,方洋旺,周晓滨.随机最优控制理论在再入机动弹头制导中的应用[J].弹道学报,2008,20(3): 92-95.
[3] 黄品秋.潘兴Ⅱ导弹和弹头的初步分析[J].导弹与航天运载技术,1994,(1):7-15.
[4] 赵汉元.飞行器再入动力学和制导[M].长沙:国防科学技术大学出版社,1997.
[5] 徐明亮,刘鲁华,汤国建,等.高超声速滑翔-巡航飞行器方案弹道设计[J].飞行力学,2010,28(5):51-54.
Researchonguidancealgorithmformobilewarheadwithpower
MENG Jing
(College of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China)
To solve the guidance problem of a mobile warhead with power, a series of guidance algorithms for descent and pull-out phase, horizontal flight phase and diving attack phase are proposed. In descent and pull-out phase, the program descent and arc pull-out guidance laws are adopted, which make sure the accurate horizontal altitude is achieved. In the horizontal flight phase, the altitude maintenance guidance law and bank-to-turn to pass the waypoints guidance law based on geometric method are designed, which aimed at improving the detecting precision and avoiding the danger areas. In the diving attack phase, multi-attack modes are given based on the basic guidance law. The guidance algorithm for each phase is validated by three dimension-of-freedom simulation, and it shows that the proposed guidance laws are practicable.
mobile warhead; guidance; waypoint; geometric method; attack mode
2011-08-03;
2011-12-01
孟京(1973-),男,河南南阳人,博士研究生,研究方向为导航、制导与控制。
V448.235
A
1002-0853(2012)02-0181-04
(编辑:崔立峰)

