基于Markov的察打无人机数据链时延建模与补偿研究
王琛, 周洲
(西北工业大学 无人机特种技术国家重点实验室, 陕西 西安 710065)
基于Markov的察打无人机数据链时延建模与补偿研究
王琛, 周洲
(西北工业大学 无人机特种技术国家重点实验室, 陕西 西安 710065)
为了改善在数据链时延情况下察打无人机的性能,对造成时延的因素及影响进行了分析,在此基础上对数据链时延进行了合理的假设和简化。并对无人机整个控制回路的各个节点的响应方式,提出了一种时间-事件-事件-时间驱动方式,使得无人机数据链的时延序列具有Markov性,同时给出了状态转移矩阵的求取方法。为了改善无人机的响应特性,采用最优控制的方法对时延进行了补偿,并基于某无人机平台验证了补偿方法的有效性。仿真结果表明,该方法的引入使得无人机的动态响应特性有了显著提高。
察打无人机; Markov链; 时延建模; 最优控制; 操纵性
引言
随着战争中对于打击高时间敏感性目标的需求以及作战人员安全的要求越来越高,侦察打击一体化无人机应运而生,且越来越受到各国的重视[1]。2003年“捕食者”无人机在阿富汗击毙“基地”组织头目的战斗就展示了其巨大的战场效力。然而,与飞行员实时进行操控的飞机不同,察打无人机需要借助数据链路来完成控制指令以及机载设备信息的传输,因而数据链路中存在的不可避免的时延就成为制约察打无人机性能的一大因素。如何精确描述数据链时延并对其进行补偿也随之成为一项重要的课题[2]。
国内对于无人机数据链时延的研究很少,并且都是把随机分布的时延转化为固定的时延从而进行性能分析和补偿研究[3],这样处理对于无人机数据链系统存在的随机时延无法准确地描述和补偿。本文创新性地在分析了数据链时延的物理诱因后引入一种新型数据驱动方式,并利用Markov理论对时延进行数学建模,得到了时延的数学模型后采用最优控制方法对时延进行了补偿研究,并得到了满意的效果。
1 数据链时延产生及影响
现今侦察打击一体化无人机的指挥是包含地面控制站的大回路控制模式,通过上行数据链将控制指令发送到无人机,再经过飞控计算机的计算、舵机的执行完成指令;通过下行数据链将无人机的状态以及采集到的信息送给地面控制站进行决策。系统示意图如图1所示。
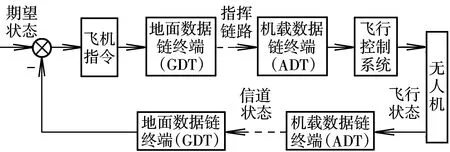
图1 侦察打击一体化无人机任务规划系统示意图
无人机数据链时延产生的因素分为4个部分:通信时延、执行时延、数据时延和扰动时延。其中影响最大的是通信时延和执行时延,通信时延是由电磁信号在空间的传输造成的;执行时延是由于解释、计算、执行控制指令等造成,包括传感器的时延、计算机运算时延等[2]。
如果将无人机大控制回路的数据链时延简化为上行时延和下行时延并用时延环节e-δt1s和e-δt2s来表示,且将飞控系统和无人机模型用C(s)和G(s)表示,简化回路如图2所示。

图2 无人机控制回路
无人机数据链加入时延后的传递函数将会变为:
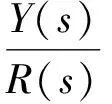
(1)
回路中特征多项式的改变,导致系统的零极点发生变化,通过以上的分析可以看出数据链时延对无人机的操纵性有影响,而不仅仅是无人机响应的滞后[3]。
2 数据链时延建模
2.1 数据链的信息传递机理和简化
无人机的主要控制节点间数据流向及主要时延因素如图3所示。

图3 数据链信息流向与主要时延图
数据表明,通信和执行时延影响占整个时延影响的90%以上[3],因此可以合理地假设在建模中只存在通信和执行时延,并在此基础上作如下假设:
(1)只考虑下行链路中的无人机状态信息而不考虑机载设备的数据,数据量很小;
(2)数据链路没有丢包;
(3)数据链路没有时序混乱。
基于以上假设,对于传感器、地面控制系统、飞控计算机、舵机分别采用时间-事件-事件-时间的驱动方式,所有控制节点采用等周期同步T采样方式,定义在k-n时刻传感器产生的控制量为uk-n,那么整个回路中的信息传输时序如图4所示。
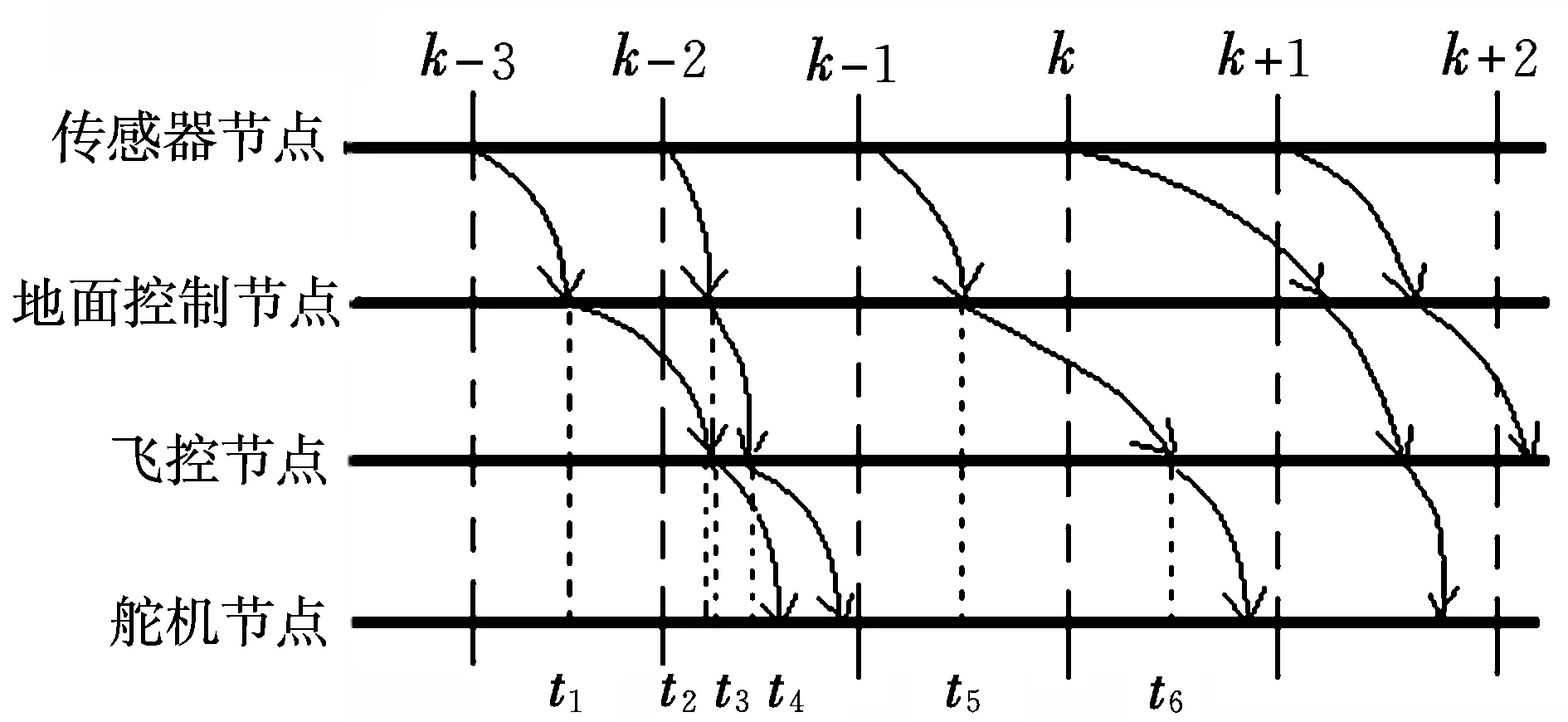
图4 无人机数据链信息传输时序图
时间驱动指节点在时钟周期的作用下定时采样信号,将信号进行处理后通过数据链送至下一节点的驱动方式;事件驱动指信息一旦到达,控制器立即对信息进行处理,并将处理信息送出的驱动方式。
设k时刻的数据链时延为dk, 规定若k时刻到达舵机的传感器信号为uk-n,则dk=k-(k-n)=n,即时延为nT个时钟周期。在k时刻没有新的信号到达,控制量仍沿用uk-2,所以时延为2T。并且每一时刻的时延是在最大时延和最小时延之间以某概率分布,并且此概率依一定规律变化。经过以上假设建模后,利用Markov理论便可以找出时延序列概率变化。
2.2 Markov链模型的建立
Markov性是指事件“未来”的状态只与“现在”有关,而和“过去”状态独立的性质[4]。基于2.1节的假设和简化后,传感器的信号是按照传感器产生信息的先后顺序到达舵机,且在同一个采样周期内舵机只能执行一个控制信号,所以“未来”的时延分布可以由“现在”的分布决定,即由k时刻时延的概率分布就可以推得k+1时刻时延的概率分布,这样无人机数据链的多步随机传输时延序列dk(k=0,1,2,…)形成Markov链。dk为采样周期的倍数,且dk∈{m,m+1,…,n},m=tmin/T,n=tmax/T,其中tmin,tmax分别为最大和最小时延。设π(k)为dk的概率分布函数,dk服从如下分布[5]:
dk~π(k)=
(2)
根据Markov链的性质有:
π(k+1)=π(k)QM(k=0,1,2,…)
(3)
式中,QM为转移矩阵。
定义转移概率:
(4)
依据式(3),由初始时延概率分布π(0)和状态转移矩阵QM就可以知道之后任意采样周期的时延概率分布π(k)。π(0)可以通过实验的方法获得,将机载时钟和基站时钟同步,给主机发送的数据打上时间戳,无人机接收时与机载时钟比对就可以计算出上行时延,类似可得到下行时延,经过多次实验就可以获得π(0)。QM可以由图2得出,下式是描述相邻时刻间时延概率分布变化的重要公式[6]。
q(i-m)(j-m)=
(5)
3 无人机模型及时延补偿方法
3.1 无人机小扰动模型
无人机有对称平面,略去机体内转动部件的陀螺力矩效应。基准运动中,对称平面处于铅垂方向且运动所在平面与飞机对称平面重合。将无人机6自由度方程采用线性小扰动简化并横纵分离,再将纵向小扰动方程离散化,得到:
(6)
当X=[ΔVΔαΔqΔθ]T时,被控对象为纵向方程;当X=[ΔβΔωxΔωyΔγ]T时,被控对象为横向方程。
3.2 时延补偿方法研究
虽然k时刻到达舵机的控制量无法完全确定,但是由2.2节可以知道到达的ui时延具有Markov性,并可以得到k时刻时延的概率分布,且状态变量方便可测,因此对系统采用全状态反馈并应用最优控制理论设计控制律,使性能指标
(7)
达到最小,令:
利用以上增广的量将式(6)和式(7)改写为:
(8)
(9)
并采用动态规划法得到满足指标式(7)的最优控制律[7]为:
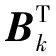
(10)
其中:
(11)
(12)
设式(11)中4个括号内表达式为eq,则其期望值为:
利用式(10)可以求出每一时刻针对此刻时延进行补偿的控制量大小,由于在每一时刻时延序列是依概率分布的,无法精确补偿,所以针对这一情况采用求期望的标准进行补偿,这也很好地结合了之前对数据链时延的Markov建模的结果。
3.3 仿真验证
为了验证本方法对时延建模和补偿方法的有效性,以某型察打无人机为平台进行仿真验证:无人机的系统时钟周期为0.02 s。无人机初始状态为Ma=0.61,h=5 000 m的定直平飞状态,仿真结果如图5所示。
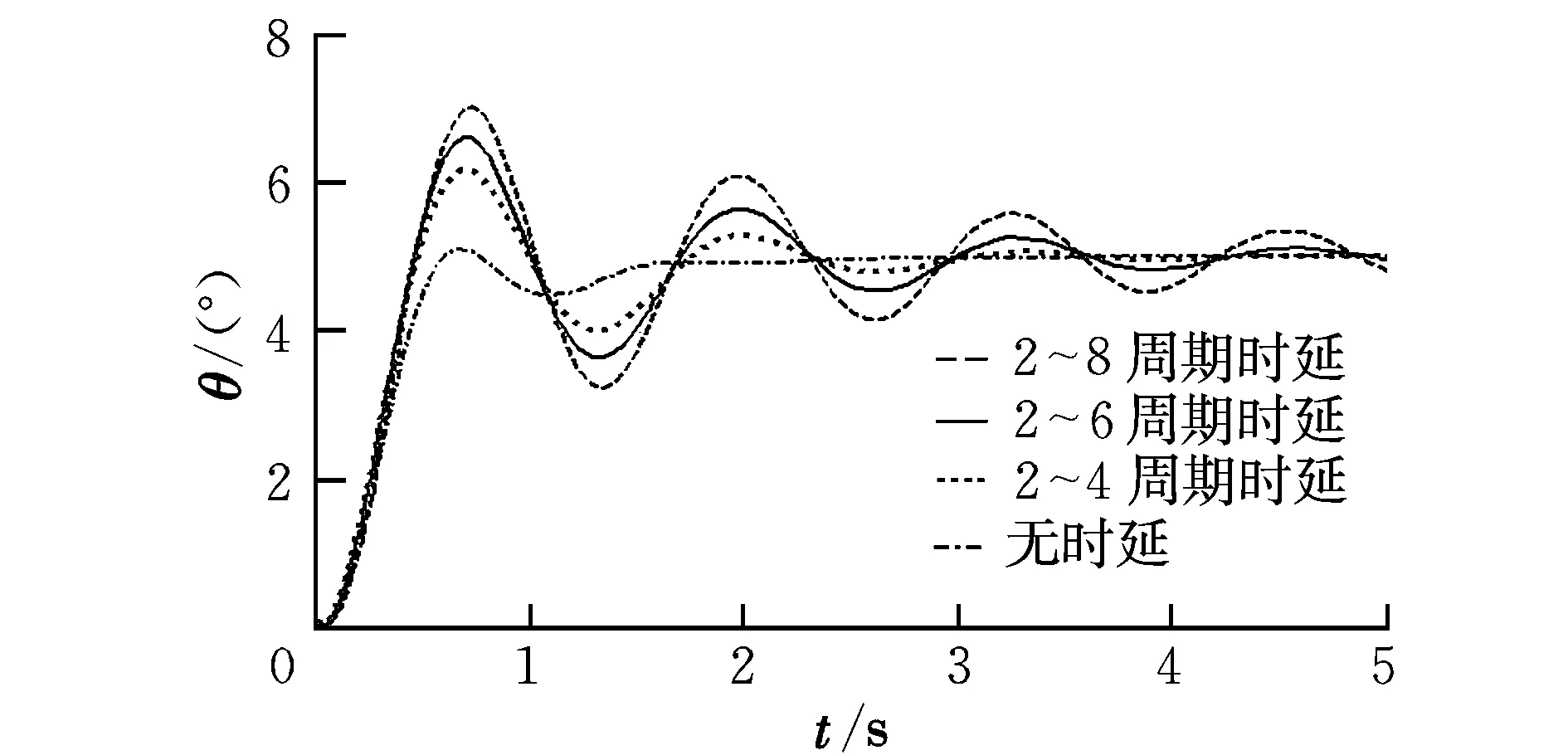
图5 未补偿时无人机俯仰角响应曲线
图5表明加入时延后无人机的响应特性明显变差,验证了之前时延会对无人机动态响应特性产生影响的理论分析。并且表明随着时延的增大,无人机的动态特性会随之变差。可以预见,时延继续增大无人机会变得不可控制。
如果假定时延范围为0.02~0.12 s,即1~6个时钟周期。输入阶跃信号,将不考虑时延、加入时延、时延补偿3种情况下无人机响应情况进行比较,结果如图6和图7所示。对比图中3种情况下无人机姿态角的响应可以看出,随着建立在Markov基础上的数据链时延的建模和最优控制法的引入,无人机的俯仰角超调量减小了47%,进入稳定的时间缩短了1.5 s;滚转角响应超调量减少了58%,进入稳定的时间缩短了1.2 s,有效地改善了无人机的动态响应特性,证明本文的建模和补偿方法是有效可行的。
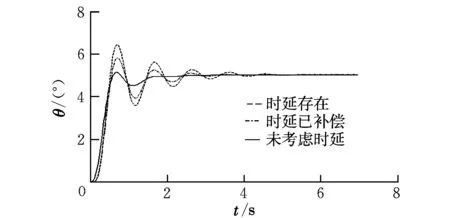
图6 俯仰角指令为5°的响应曲线
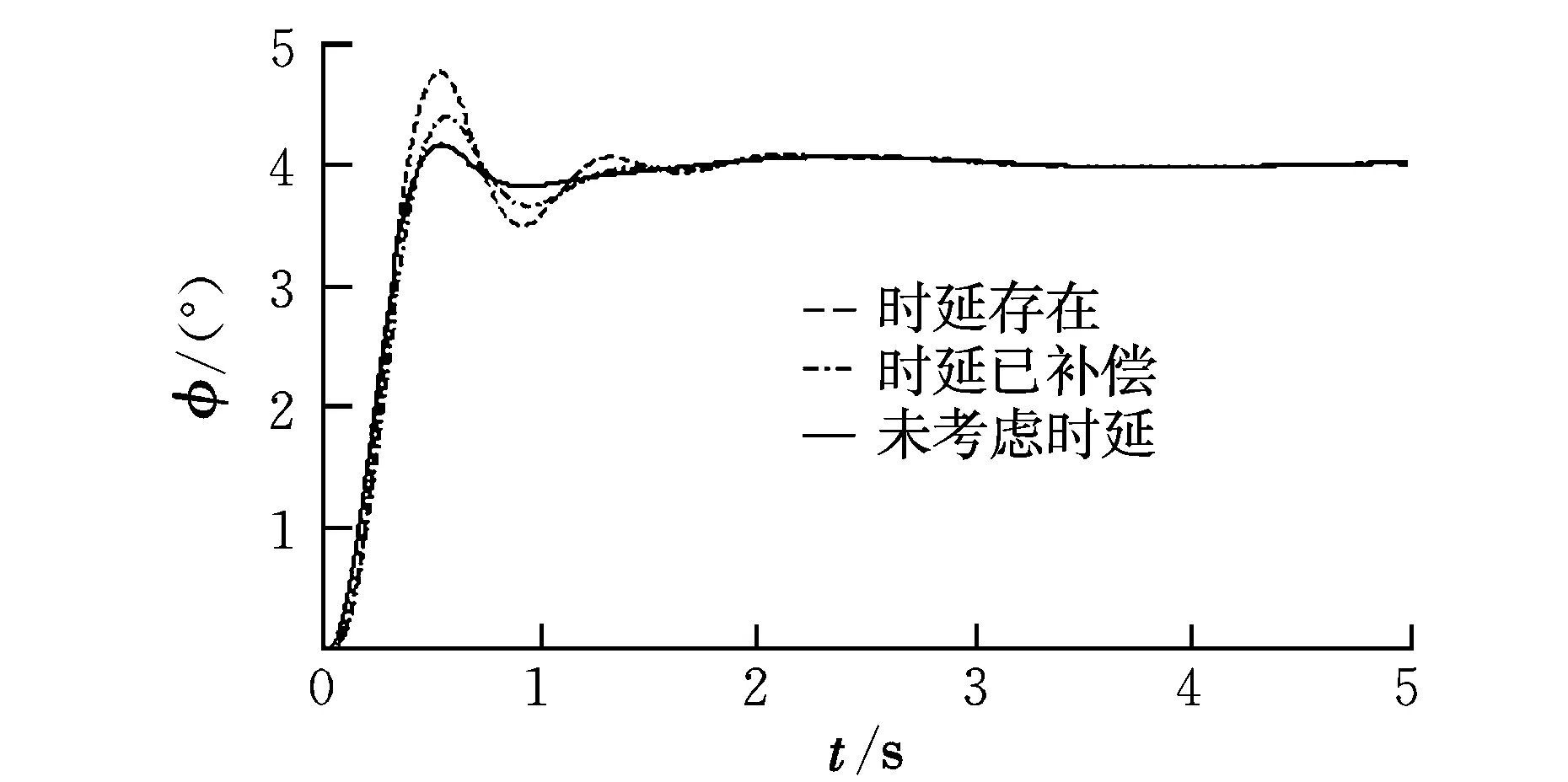
图7 滚转角指令为4°的响应曲线
4 结束语
通过本文研究表明,随着无人机时延的增大,无人机的动态响应特性逐渐变差,并且当延时增大到一定程度,无人机将变得难以控制,因此在进行数据链设计时应尽量减小时延以保证无人机性能。经过本文中的对于数据链时延的建模和补偿后,无人机的动态响应特性明显改善,说明了基于Markov的建模和采用最优控制方法进行补偿是有效可行的。由于提高时延建模的精度对于补偿方法的改进至关重要,未来改进时延的描述算法是非常有必要的。
[1] Mulder J A.Unmanned aircraft systems roadmap,2005-2030[R].Office of the Secretary of Defense of USA,2004:105-106.
[2] Paul G Fahlstrom,Thomas J Gleason.Introduction to UAV Systems[M].Maryland:Uavsystems Inc,2007:20-21.
[3] 陈占海.侦察打击一体化无人机数据链延时影响研究[D].西安:西北工业大学,2010.
[4] 张波,商豪.应用随机过程[M].北京:中国人民大学出版社,2009.
[5] 代双凤.网络控制系统的Markov建模设计与分析[D].秦皇岛:燕山大学,2008.
[6] 于之训,陈辉堂,王月娟.基于Markov延迟特性的闭环网络控制系统研究[J].控制理论与应用,2002,19(2):263-267.
[6] 吴受章.应用最优控制[M].西安:西安交通大学出版社,1986.
ResearchonmodelingandcompensationmethodfordatalinkdelayofRSIUAVbasedonMarkovtheory
WANG Chen, ZHOU Zhou
(National Key Laboratory of Science and Technology on UAV, NWPU, Xi’an 710065, China)
This paper improves the performance of RSIUAV while considering the datalink delay. At the beginning, this paper analyzes the factors which induce the delay, reveals the influence of the delay and makes reasonable assumption and simplification to datalink delay. Then, in order to get the datalink delay to observe Markov chain, the paper gives a brand new data-driven mode, the corresponding Markov state transition matrix is given also. Finally, for compensating the delay, this paper uses optimal control method and verifies the effect based on a kind of RSIUAV. The simulation result shows that the application of modeling and compensation method distinctly improves the dynamic corresponding characteristic of RSIUAV.
RSIUAV; Markov chain; modeling of time delay; optimal control; maneuverability
2011-10-06;
2011-12-20
王琛(1987-),男,陕西西安人,博士研究生,研究方向为飞行力学与控制。
V279
A
1002-0853(2012)02-0147-04
(编辑:方春玲)

