改善箭机分离载机飞行品质的状态反馈器研究

张艳华, 李华星, 张登成, 胡孟权, 张久星

(1.西北工业大学 航空学院, 陕西 西安 710072;2.空军工程大学 工程学院, 陕西 西安 710038)

改善箭机分离载机飞行品质的状态反馈器研究

张艳华1, 李华星1, 张登成2, 胡孟权2, 张久星2

(1.西北工业大学 航空学院, 陕西 西安 710072;2.空军工程大学 工程学院, 陕西 西安 710038)

为了改善内装式运载火箭与载机分离过程载机的飞行品质,应用现代控制理论,以一组期望的闭环极点为设计目标,利用正比于状态变量的线性控制律,设计带有状态观测器的状态反馈系统。通过Bass-Gura法求解反馈增益,基于时域分析法数值模拟了带有状态反馈器飞机的飞行品质。仿真结果表明,长、短周期运动变为收敛的周期模态,飞行品质提高到1级标准,可见状态反馈器设计是一种改善箭机分离过程载机飞行品质的高效可行的方法。

飞行品质; 状态反馈器; Bass-Gura法

引言

内装式空中发射运载火箭为快速、灵活、可靠、廉价地发射一定重量的运载火箭提供了一种高效的解决途径,成为近年来国内外广泛开展的一项研究热点,研究内容的一个重要方面就是如何保障运载火箭与载机分离过程安全高品质的完成。分离过程[1]可分为运载火箭相对于载机开始运动到其质心刚好出舱和运载火箭质心出舱到整个火箭完全出舱两个阶段。第一阶段由于分离过程经历时间短,载机重心位置变化急剧,飞行员的操纵难度加大,载机的稳定性、操纵性等飞行品质以及安全性都会受到严重的影响,如何保证分离过程安全高品质的完成就成为急需解决的问题。飞行品质变差的根本原因在于火箭移动过程中系统状态方程的特征根发生变化,出现了不稳定区域,导致稳定性和操纵性变差。本文根据现代控制理论中状态反馈极点配置的原理[2],通过选取合适的状态反馈增益k,使闭环系统的极点即特征值恰好处于所希望的一组闭环极点的位置上。通过这种方法可以有效地改善和提高载机在分离过程中的飞行品质,进而为空投过程安全高品质地完成提供有力的保障。

1 状态反馈系统设计

1.1 系统的可控性和可观测性

将包含运载火箭的载机作为研究的系统,在飞机的控制问题中,首先关注的是一个动态系统的状态是否被控制输入影响以及系统的状态是否可以由系统的输出确定下来,即状态反馈设计中的可控性和可观测性,这是控制理论中极其重要的两个基本问题,也是所设计的反馈器是否适用的充分条件。

建立载机纵向无量纲的线化小扰动状态方程:

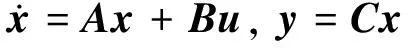
(1)

式中,x为状态变量;u为控制或输入变量;y为输出变量;A为系统矩阵;B为控制或输入矩阵;C为输出矩阵。分别表示为:

(2)

(3)

(4)

(5)

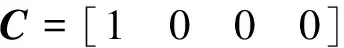
(6)

式(3)～式(5)中气动导数的含义详见文献[3]。系统完全可控的充分必要条件是可控性矩阵V的秩等于状态向量的维数。矩阵V由矩阵A和B以如下方式构成:

计算得到载机的可控性矩阵V的秩等于状态向量的维数(=4),说明本文研究的系统是可控的。

一个系统完全可观测的充分必要条件是可观测矩阵U的秩等于状态向量的维数,矩阵U的定义为:

计算得到载机的可观测矩阵U的秩等于状态向量的维数(=4),说明本文研究的系统是可观测的。

1.2 状态反馈系统

根据前面所述,系统具有可控性和可观测性,可进一步设计状态反馈器。系统设计问题旨在寻找一种控制规律,使得在其作用下系统运动的行为满足期望的性能指标,如果性能指标达到或好于期望性能指标就实现了设计目标。根据本文研究问题的特点,期望的性能指标就是载机的飞行品质等级,通过设计基于一定控制律的状态反馈器,获取一组期望的闭环极点(或自振频率和阻尼比),就达到了改善和提高载机飞行品质的设计目标,所以问题的关键就在于确定反馈器的控制律。

在状态反馈设计中,假设线性控制律正比于状态向量,即

η=-kTx+ηp

式中,kT为反馈增益向量的转置;ηp为驾驶员输入。把控制律代入状态方程,得到:

(7)

设A*=A-BkT,称A*为增强矩阵。

Bass-Gura法[4]是一种常用的求解反馈增益进而确定控制律的方法,该方法简化了矩阵计算,只要应用该方法求解下面的方程即可。

(8)

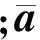
在本文研究问题中,希望的特征根是以长、短周期阻尼比和无阻尼自振频率的形式表示的,特征方程可以用希望的阻尼比和无阻尼自振频率表示为:

展开后得到闭环系统的特征方程为:

开环系统的特征方程为:

λ4+a1λ3+a2λ2+a3λ+a4=0

则:

对于4阶可控性矩阵V,可表示为:

如果矩阵A不是伴随式矩阵,则需要一个变换矩阵W,变换矩阵由系统矩阵特征方程的系数组成,对于4阶系统,变换矩阵表示为:

基于上面的几个矩阵和向量的表达式,根据式(8)即可得到反馈增益,从而进一步确定控制律。

由于状态变量为系统的内部变量,通常并不是每一个状态变量都是可以直接测量的。为了实现状态反馈,就要利用可测量变量,即设计状态观测器问题,一般根据观测器比被观测系统的响应稍微灵敏一点的原则设计状态观测器,得到观测器增益,最后就构成了包含状态观测器的状态反馈控制系统,如图1所示。

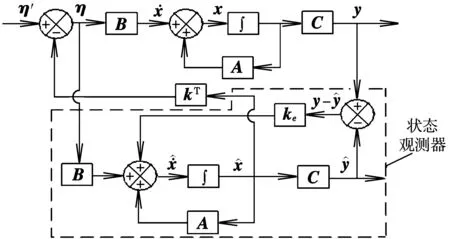
图1 包含状态观测器的状态反馈系统

2 具有状态反馈系统载机的飞行品质

为保证载机在火箭移动的整个过程中都具有1级飞行品质,现针对迎角静稳定度最差的情况(即火箭质心刚好在出舱位置)设计状态反馈器,提出1级飞行品质设计要求:ωnsp=1.6,ζsp=0.8,ωnp=0.1,ζsp=0.05。

根据Bass-Gura法,计算得到火箭质心刚好出舱位置状态反馈系统的反馈增益为:

k=[0.5507 -1.4703 -0.0077 -0.0608]

根据反馈增益确定控制律,将基于此控制律的状态反馈系统应用到火箭移动的整个过程中,根据增强系统状态方程(7)计算载机的纵向短、长周期模态特性,短、长周期模态阻尼比随火箭移动的变化曲线分别如图2和图3所示,其中实线表示原系统,虚线表示包含状态反馈器的增强系统(图4、图5中相同)。图2中原系统短周期模态由周期性衰减运动变为非周期性衰减运动,且操纵期望由等级1逐渐下降为等级2;增强系统则全为周期性衰减运动,阻尼比0.64≤ζsp≤0.80,操纵期望0.278≤CAP≤0.434,对照飞行品质规范[5],均满足1级飞行品质要求。图3中原系统长周期模态由周期性的衰减运动变为周期性的发散运动,降低了飞行品质;增强系统整个过程都为周期性衰减运动,不存在阻尼比小于零的发散区域,且满足飞行品质等级1要求。

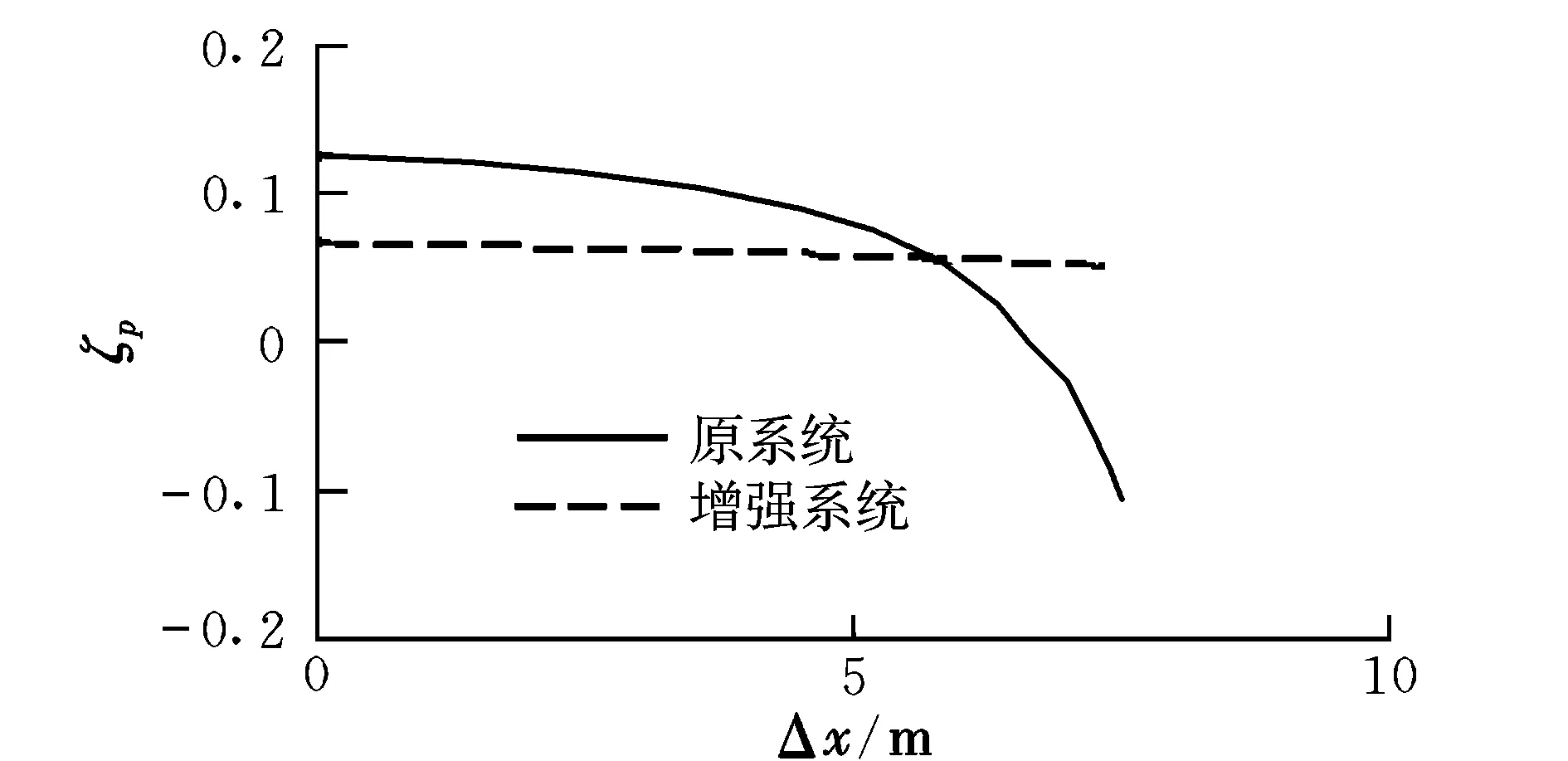
图3 ζp的变化规律

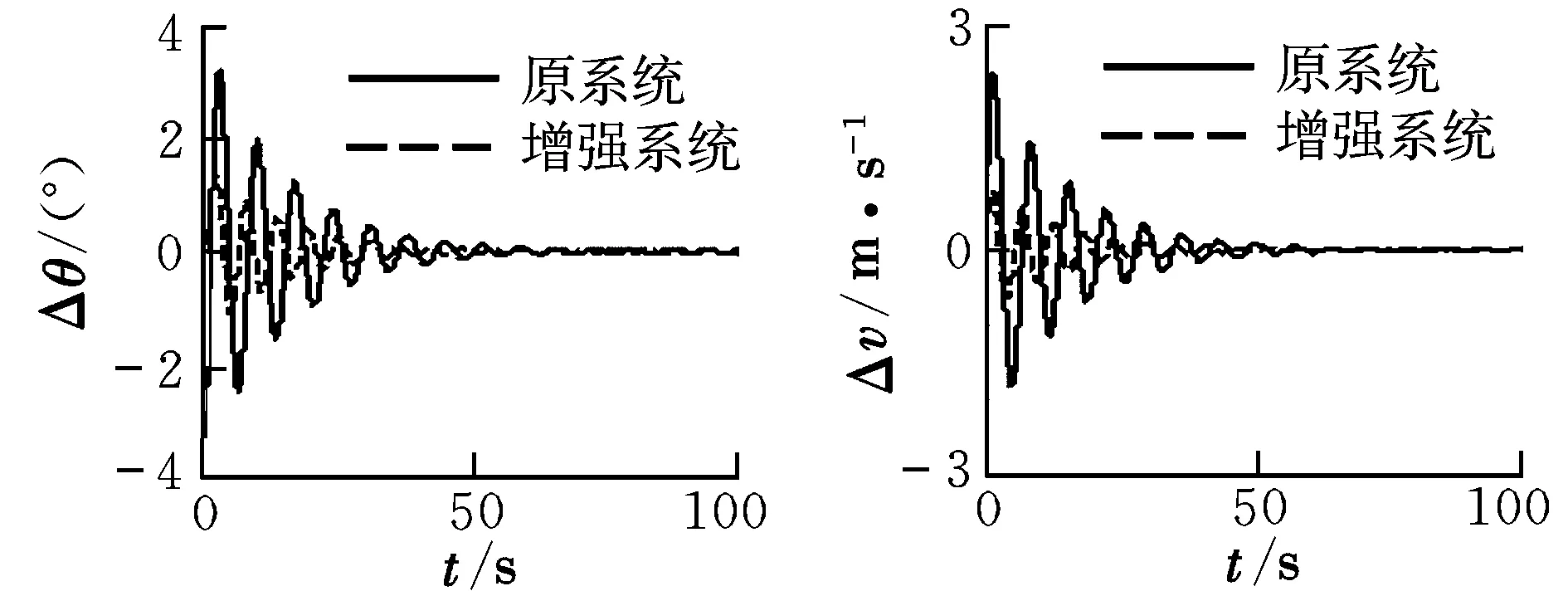
图4 运载火箭在初始位置Δθ和Δv的时间响应

图5 运载火箭在出舱位置Δθ和Δv的时间响应

利用时域分析法数值模拟载机在升降舵脉冲偏转时俯仰角增量Δθ和平飞速度增量Δv的时间响应,运载火箭在初始位置和出舱位置时Δθ和Δv的响应曲线分别如图4和图5所示。结果表明通过设计状态反馈系统,初始位置处脉冲输入响应的超调度减小,调整时间变短,动操纵性变好;出舱位置处由原来发散的周期模态变为收敛的周期模态,与增强系统的长周期阻尼比变化一致,大大提高了载机的操纵性。

3 结论

(1)基于一定反馈增益设计了包含状态观测器的状态反馈系统,纵向长、短周期的飞行品质均提高到等级1;

(2)升降舵脉冲输入后过渡过程的超调量和调整时间大大减小,改善了载机操纵性方面的飞行品质,减小了飞行员的操纵难度。

可见状态反馈器设计是保证分离过程安全高品质完成的一种高效可行的方法。

[1] 张登成,阎杰,张久星.内装式空射运载火箭与载机分离研究[J].弹箭与制导学报,2009,29(5):158-161.

[2] [美]尼尔森 R C.飞行稳定性和自动控制[M]. 顾均晓,译.北京:国防工业出版社,2008:337-376.

[3] 高金源,李陆豫,冯亚昌,等.飞机飞行品质[M].北京:国防工业出版社,2003:51-97.

[4] 陈廷楠.飞机飞行性能品质与控制[M].北京:国防工业出版社,2007:109-126.

[5] 国防科学技术工业委员会.GJB185-86 有人驾驶飞机(固定翼)飞行品质[S].北京:国防科学技术工业委员会,1986.

Studyonstatefeedbacksystemtoimproveflightqualitiesofcarrieraircraftduringlaunchvehicleseparationfromaircraft

ZHANG Yan-hua1, LI Hua-xing1, ZHANG Deng-cheng2, HU Meng-quan2, ZHANG Jiu-xing2

(1.College of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China;2. Engineering Institute, Air Force Engineering University, Xi’an 710038, China)

In order to improve the flight qualities of carrier aircraft during launch vehicle separation, the state feedback system with state observer based on modern control theory was designed in order to get the expected close-loop apices, and linear control laws proportion to state variables were adopted. The feedback gain was calculated through the method called as Bass-Gura, and the time-domain method was applied to the simulation of long and short cycle modes. The results show that long and short cycle modes are both periodicity and convergence, and the flight quality satisfies grade one. Obviously the state feedback system is a very efficient and adapted method to improve flight qualities of aircraft.

flight qualities; state feedback system; Bass-Gura method

2011-05-13;

2011-10-13

国家“863”基金资助(2010AA7020401)

张艳华(1979-),女,内蒙古赤峰人,讲师,硕士,研究方向为飞行力学与飞行仿真。

V212.1

A

1002-0853(2012)02-0113-04

(编辑：王育林)