朱集矿深井软岩巷道大变形机制及其控制研究
黄 兴,刘泉声,,乔 正
(1. 中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室,武汉 430071;2. 山东科技大学 土木建筑学院,山东 青岛 266510)
1 引 言
随着对能源需求的增加和开采强度的不断增大,浅部资源日益减少,国内外许多矿山都相继进入深部资源开采状态[1]。与浅部开采相比,深部采区的地质构造、应力场特征、煤岩体的破碎性质与动力响应特征、岩层移动以及能量的积聚释放规律均发生了显著变化,深部矿井动力灾害的致灾机制、触发条件、演化规律以及显现特征均不同于浅部煤矿工程。进入深部开拓阶段后,深部岩体处于“三高一扰动”(高地应力、高渗透压力、高地温梯度和强烈采掘扰动)相互耦合的复杂环境,随之发生的非线性大变形动力现象尤为突出[2-3]。主要表现为巷道变形量大(顶沉、底膨和侧胀等)、变形时间长、围岩破碎严重,支护体(锚杆、锚索等)失效增多,巷道维护十分困难,尤其以底臌问题最为突出。
朱集煤矿-885 m东翼轨道大巷埋深为950 m,巷道开挖后围岩发生了大变形,底臌严重,严重制约矿井安全生产和经济效益。因此,本文将针对该巷道揭示其大变形机制,并提出相应的控制措施。
2 工程概况
淮南矿业集团朱集煤矿-885 m东翼轨道大巷埋深为 950 m,断面形状为直墙半圆拱形,净宽×净高=5.4 m×4.7 m,是连接井底车场与首采区的轨道运输大巷,要求服务年限长,对巷道变形控制严格,关系到该矿的正常生产和运营。围岩主要为花斑泥岩,岩层大致为水平向。
-885 m东翼轨道大巷处于东翼巷道群,该巷道群巷道断面大,布置密集,属于高应力软弱围岩大断面巷道群。由于密集布置的大断面巷道分布于大规模松软围岩中,东翼轨道巷受相邻巷道——回风巷(南)及胶带机巷开挖扰动和二次应力场相互叠加影响,使巷道不断产生较大变形,底臌、顶沉严重,多数U型棚歪斜,轨道偏斜及底板出现多处裂缝等,导致巷道整体失稳破坏。
2.1 原支护形式
-885 m东翼轨道大巷综掘后采用29U型钢支架一次支护+预应力锚索二次支护及滞后喷注浆作为开挖后的围岩损伤修复与补强加固。支护参数如表1所示。

表1 原支护材料及规格参数Table 1 Former supporting materials and specifications
2.2 -885 m东翼轨道大巷矿压监测
在-885 m东翼轨道大巷设置了3个表面位移测站进行矿压观测,监测巷道表面位移,监测结果如图1、2所示。
从上述矿压观测结果可以看出,巷道开挖后,巷道变形剧烈,两帮收敛、底臌均较大,变形速率大。

图1 帮部收敛量图Fig.1 Convergence magnitude of walls

图2 底臌量趋势图Fig.2 Displacement curves of roadway floor
2.3 围岩大变形特征
朱集煤矿-885 m东翼轨道大巷开挖后,裂隙萌生和扩展的速度很快,两帮收敛量大,拱顶下沉量大,部分 U型钢支架顶部呈压扭状,底臌量达300~500 mm,底臌速率大,轨道倾斜,部分区段的巷道底板出现较密集的张性裂缝(见图3),掘进时需要频繁翻修(如卧底等)。具体表现为:
(1)巷道来压迅速,开挖后由于原始地应力重新分布,围岩变形迅速,矿压显现剧烈,巷道掘进时的顶、底板移近速率高达30 mm/d;
(2)流变性显著,巷道掘进和返修后较长时间仍不能稳定,变形速率仍较高;
(3)对应力扰动极为敏感,相对稳定的巷道一旦受到相邻巷道掘进扰动影响,则围岩变形再次急剧增大;
(4)顶底板相对移近量大于两帮移近量,且底臌非常严重。

图3 巷道变形破坏实照Fig.3 Photos of deformation and failure of roadway
3 -885 m东翼轨道大巷变形破坏机制
-885 m东翼轨道大巷从开挖到采取原支护产生的变形量大,变形速率大,破坏严重,底板多处出现沿走向发展的张性裂缝。
3.1 深部软岩巷道大变形等级
1946年,Terzaghi首次提出了挤出性岩石和膨胀性岩石的概念[4-5]。受到 Terzaghi思想的影响,人们一般把大变形机制分为以下两类:一是挤压性变形;二是膨胀变形。
Hoek等[6]针对软岩大变形问题,给出了洞壁位移与巷道半径的百分比——岩体强度与地应力之比关系图,在图中划分了挤压变形程度等级,可以有效地判断挤压性变形等级如图4所示。
根据现场监测,885 m轨道大巷的表面位移平均达300~450 mm,巷道跨度为5400 mm,因此,其收敛应变为5%~10%。围岩强度与最大初始地应力比值也在0.2范围内,表示岩体软弱,围岩初始地力水平相对较高,对应图4中D区,由此可知,该巷道围岩处于非常严重的挤压性大变形状态中。应加强围岩支护控制围岩挤压性变形。
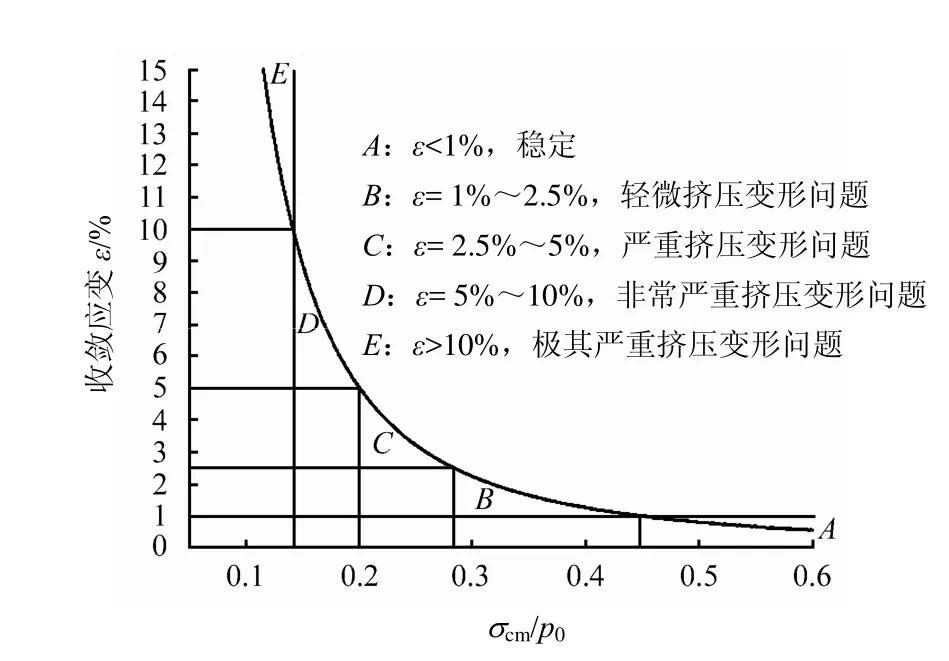
图4 围岩变形等级判断示图[6]Fig.4 Classification of surrounding rock deformation[6]
3.2 巷道应力场、位移场力学分析
地应力是影响巷道围岩变形的重要因素之一[7]。朱集矿-885 m东翼轨道大巷埋深950 m,埋深大,地应力的最大主应力高达31.2 MPa。
开挖前后岩体水平应力的分布状况如图 5所示。开挖前,巷道围岩处于原岩应力场中,岩体处于三向应力平衡状态。开挖后,围岩内部应力重新分布,巷道表面径向应力降为 0,环向应力增加。施加支护后将支护反力简化为均布荷载pi。
关于轴对称圆形巷道开挖问题已经有很多种解析方法了,如弹塑性、弹脆性和弹性应变软化模型[8-10],但大都使用的是线性摩尔-库仑弹塑性屈服准则,然而深部岩体变形往往表现出明显的非线性变形特征,因此,在这里采用非线性的Hoek-Brown强度准则[10]。
设图5的巷道断面为圆形,巷道无限长,围岩为连续、均质、各向同性、初始线弹性,原岩应力为静水压力状态(p0),将支护体视为独立于围岩的结构体等效径向支护反力为。当巷道开挖后,围岩将产生径向位移,形成塑性区,当围岩应力达到初始屈服应力后,围岩强度急剧降低,表现出峰后应变软化特性,在此采用弹脆性模型计算,如图6所示。
(1)应力分析
围岩体采用非线性的Hoek-Brown强度准则,
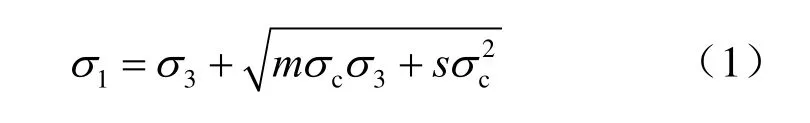
式中:σ1、σ3为破坏时的最大、最小主应力;σc为单轴抗压强度;m、s是Hoek-Brown强度准则中的常数。
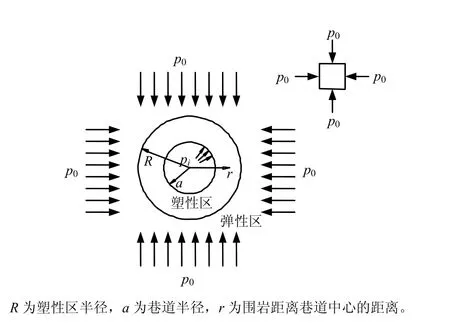
图5 无限体中的轴对称圆形巷道Fig.5 A circular roadway in an infinite medium
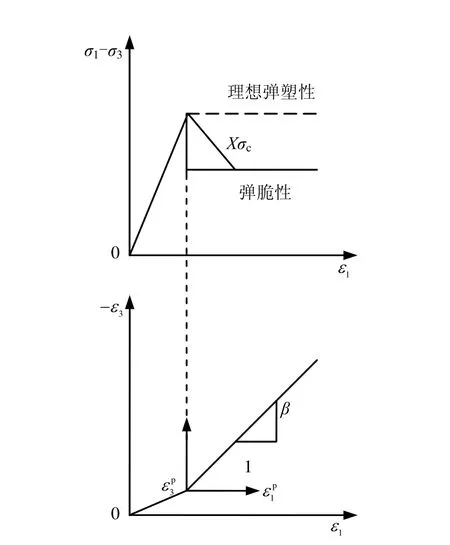
图6 围岩力学模型Fig.6 Mechanical model of surrounding rock
对于圆形巷道,σ1=σθ,σ3=σr,式(1)可以写成为
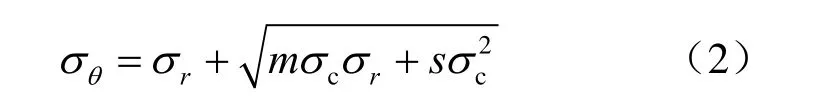
对于塑性区a≤r≤R(见图5)处,上式可写成为
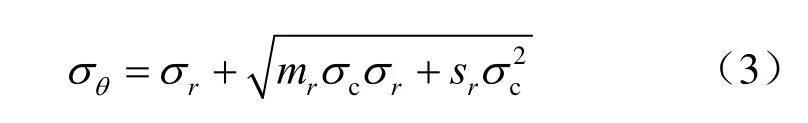
平衡微分方程为
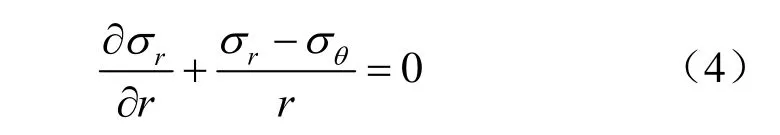
应力边界条件为

将式(3)代入式(4)得
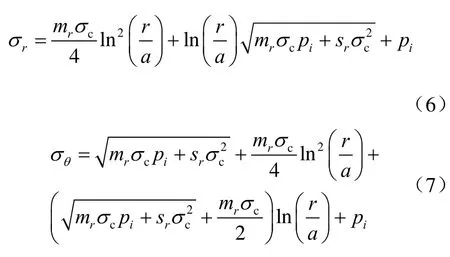
(2)塑性区半径
在弹、塑性交界面上(r=R),σcr=σc,可得出塑性区半径数值解,
(3)弹性区位移
将 r=R代入式(6)中,得弹性区、塑性区交界面上应力Rσ,
弹性区的径向、周向应力和径向位移为

表面位移u的负号表示位移指向巷道中心。
(4)塑性区位移
塑性区中的径向应变εr、周向应变εθ可以写成
式中:e表示弹性部分;p表示塑性部分。有
假设弹性变形相对塑性变形较小,并遵循非关联流动法则,则径向应变和周向应变的塑性部分有以下关系:
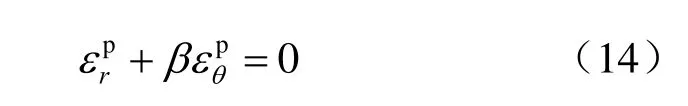
式中:β为剪胀角ψ的函数,β=(1+sinψ)/(1-sinψ),
据式(11)~(14)有以下微分方程:
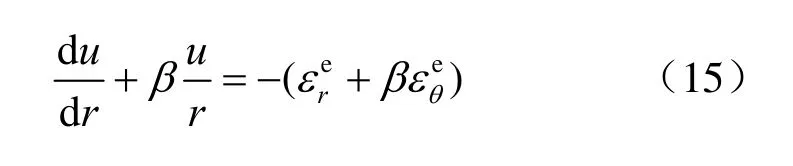
式(15)可以通过边界条件求解出弹性区和塑性区边界处的径向位移uR:
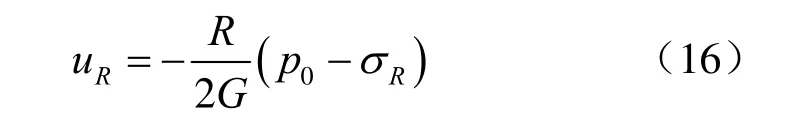
塑性区的径向位移表达式为
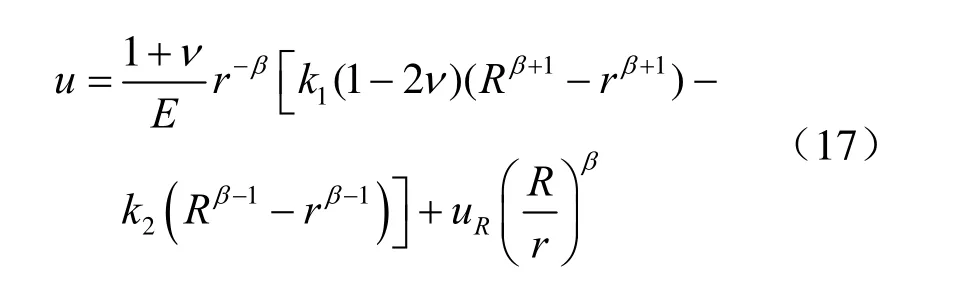
开挖轮廓表面位移u0(r=a)为
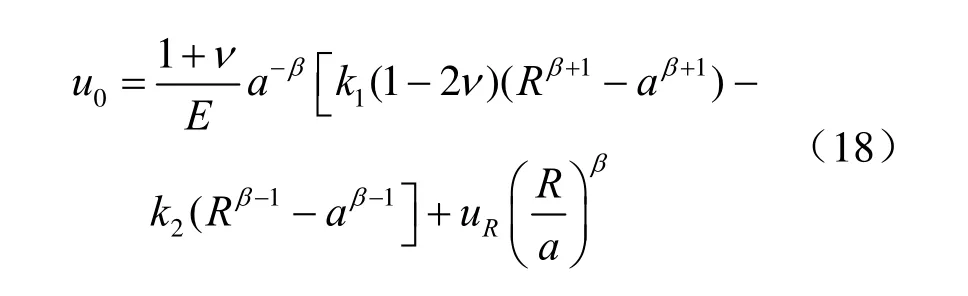
其中,
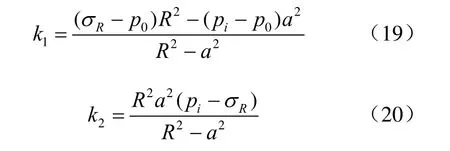
(5)朱集东翼轨道大巷表面位移弹塑性解对于巷道表面r=a处,有 σR=pi,且

而弹性区与塑性区交界处位移相对巷道表面位移较小,可将式(18)中最后一项删去,简化得

将东翼轨道大巷围岩力学参数(见3.7节)代入式(22),可以粗略计算巷道围岩表面位移,u0约为150 mm。考虑围岩蠕变,位移将更大。
3.3 围岩强度特性
围岩的物理力学性质也是影响深井岩巷支护的重要因素。-885 m东翼轨道大巷围岩主要为花斑泥岩,岩层软弱、强度低,在巷道开挖前就已发生部分塑化,岩体自身强度直接影响自身承载能力的大小。
花斑泥岩具有遇水膨胀的特性。巷道采用综掘开挖,开挖粉尘量大,掌子面和已掘巷道需要频繁地喷雾降尘,而该巷道并未及时修筑水沟排水,掘进后未及时采取喷浆等配套措施,巷道围岩未及时封闭。对于膨胀性极强的岩石,巷道开挖后因锚杆锚索施工用水、岩石吸收空气中的水分或因水沟渗水等原因导致围岩中水分含量增加时,围岩即发生膨胀;当季节性通风湿度变化导致围岩失水时,围岩会发生收缩开裂疏松,导致其完整性和整体强度降低甚至丧失。因此,巷道开挖后必须首先封闭围岩,避免围岩中的水分增加或流失,导致围岩膨胀大变形失稳或干裂疏松破坏失稳。
3.4 巷道断面形状
目前煤矿巷道通常采用梯形或直墙拱形等形状,由于底板不能形成稳定的拱形结构使得底臌量增大。数值计算表明,在所有条件都相同的情况下,直墙半圆拱的底臌量比圆形巷道底臌量大 1/3以上。现有研究表明,巷道的顶底板岩层性质和支护状况基本相同的条件下,只是巷道顶底形状上的差异,就可使底臌量比底板下沉量增大1/3左右[12]。
-885 m东翼轨道大巷断面大,直墙拱形断面与圆形断面相比较,前者应力集中大,破坏严重。从图7可以看出,深部巷道变形后,自动趋向于圆形断面发展。从数值模拟中也可以看出,当采用直墙拱形巷道断面时,在肩窝和底角处将出现剪应力集中区。

图7 直墙拱形巷道断面向圆形断面收缩Fig.7 Shape of the roadway contracts to circle
3.5 相邻巷道开挖扰动影响
朱集矿井开拓过程中,-885 m东翼轨道大巷处于密集布置的大断面大规模松软围岩巷道群中,受相邻平行掘进的回风巷(南)和胶带机大巷开挖扰动影响。巷道开挖扰动区和二次应力场相互叠加,又受高地应力影响,从开始建设时起,巷道不断产生变形(底臌变形超过 450 mm)而破裂失稳,巷道破坏严重,因而不得不多次重复返修,给矿井生产带来重大损失。
图8显示了相邻巷道对轨道大巷的扰动影响关系。其中u1为t1时间段内轨道大巷开挖自身变形,u2为轨道大巷t2时间段内受相邻的回风巷南开挖扰动影响后的变形,u3为为轨道大巷t3时间段内受相邻的胶带机巷再次开挖扰动影响后的变形。

图8 -885 m东翼轨道大巷受相邻巷道开挖扰动影响示意图Fig.8 Deformation of -885 m east wing rail roadway disturbed by adjacent excavation
3.6 底板未支护
-885 m轨道巷开挖后,顶部肩窝及底部墙角处应力集中,处于剪应力集中区。原支护结构不合理,原支护中的U型钢架及肩顶锚索这两种支护形式虽能提供较大的支撑力阻止帮顶变形,但由于未进行底板支护,而不能阻止底鼓发生,因此,该巷道底膨严重,进而使帮墙失稳,支护结构支撑力逐渐降低,使得底膨、帮墙凸出现象日趋严重。
此外,该轨道巷U型钢架壁后采用碎石充填,长时间未进行喷浆和注浆补强,壁后所充填的碎矸石没有胶结成一整体,造成U型钢支撑体系与围岩之间接触不均匀,从而降低了U型钢支撑体系承载能力。
3.7 数值计算研究
数值计算采用Flac3D程序,该程序能够模拟围岩大变形。围岩材料力学参数:重度γ=25 k N/m3,弹性模量E=3 GPa,泊松比ν=0.30,抗拉强度σt=1 MPa,凝聚力c=0.9 MPa,内摩擦角φ=30°。巷道净断面尺寸为:5400 mm×4700 mm。地应力:竖直应力为22 MPa,水平应力为26.5 MPa。
朱集煤矿东翼巷道群数值模型如图9所示。
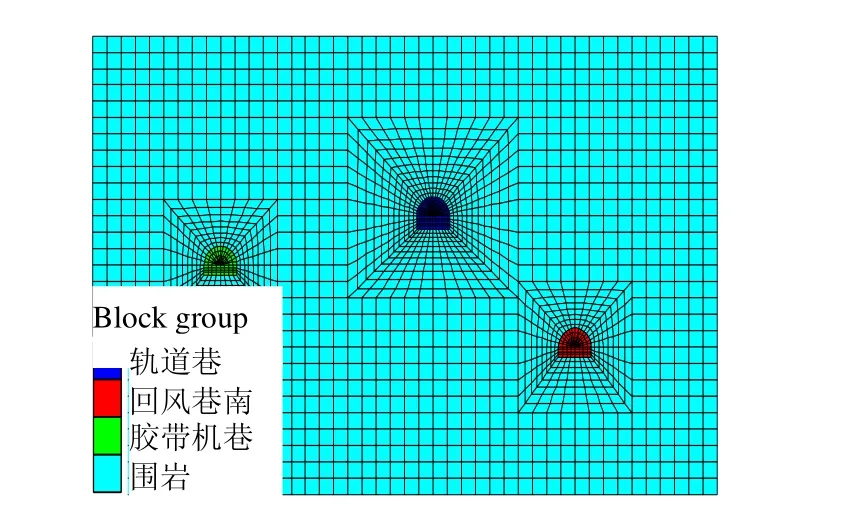
图9 朱集矿东翼巷道群布置图Fig.9 Layout of the east wing roadway group
(1)原支护模型
巷道在原支护方案下的数值计算模型见图10。
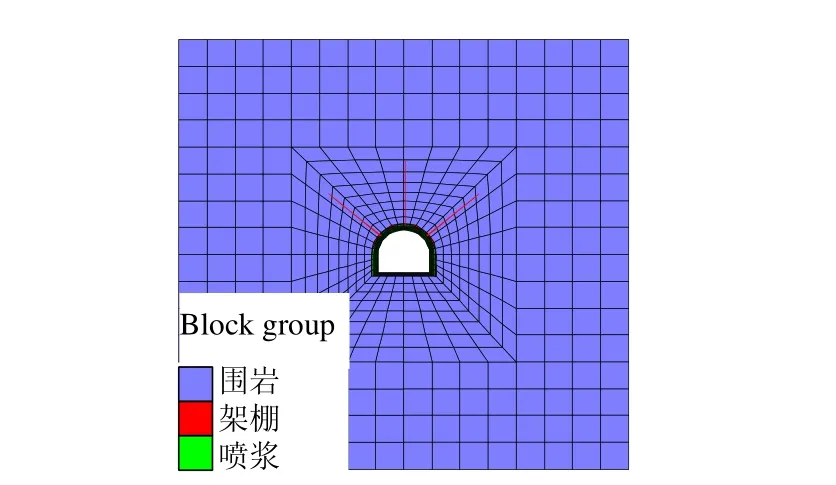
图10 巷道原支护模型图Fig.10 Original supporting model of roadway
(2)计算结果
图11为数值计算结果,图中显示,巷道开挖后在原支护方案下,围岩变形量大,塑性破坏区范围大,支护不合理。
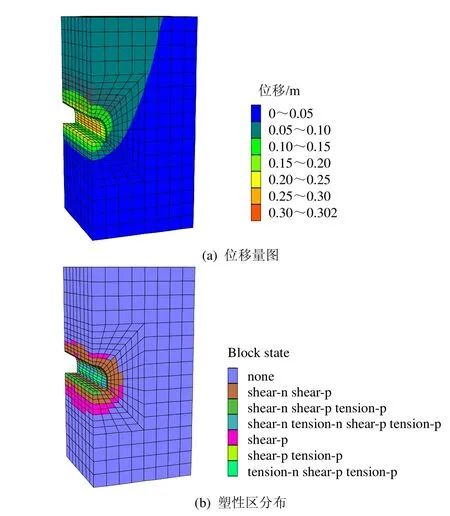
图11 原支护方案计算结果Fig.11 Computational results of the original support
4 新支护技术措施
巷道开挖后肩窝和帮角处处于剪应力集中区,大断面软岩巷道支护必须进行底板支护,抗隆起和抗剪切滑移,而且必须要具备足够的支护强度,形成封闭支护。
数值模拟和现场松动圈实测结果表明,对于这种直墙拱形巷道,边墙下部直到底板标高以下 2~3 m甚至更大范围内的围岩进入破裂滑移状态,底板破损区范围一般大于两帮和拱顶,这主要是巷道底板与边墙相交的两角处应力高度集中及底板中间部位拉应力的作用造成的。因此,必须对深部岩巷的底角部位采取有效的抗剪切滑移的支护措施,在底板中间部位采取抗隆起支护措施,以增强帮脚和底角周围应力集中区岩体的抗剪强度及抗滑移变形的能力和底板中部围岩的抗拉强度及抗隆起变形的能力。
针对-885 m东翼轨道大巷开挖后在原有支护基础上出现大变形,采取新支护措施的主导思想是增强围岩自身抗压强度和支护结构的抗变形能力,尤其重视底板支护。
针对目前-885 m东翼轨道巷两帮收敛量大,底臌量大,在原支护的基础上提出以下支护加固方案:
(1)因为帮部挤出量较大,因此,在两帮距底板1.7 m处各施作一根φ22 mm,L=6.3 m锚索,在两帮距底板1.2 m处各施作一根φ22 mm,L=2.5 m锚杆。
(2)在两帮距底板0.3 m处按俯角为30°各施作一根φ22 mm,L=2.5 m的帮脚锚杆,起应力集中区抗剪加固的作用。
(3)进行底板注浆。距边墙为1.2~1.5 m,挖槽深为0.7 m,注浆孔深为2.0 m,排距为2.1 m,6分注浆管长为1.5 m。
(4)为有效地进行底臌治理,在底板注浆后,尽快施工底板注浆锚管。
在底板两端距边墙0.2 m的位置按外倾15°各施作一根长度L=3.5~5 m的底角注浆锚管,注 浆锚管为φ48 mm×3.5 mm的花管,即作注浆花管。
注浆管为脚手架花管,φ=48 mm,壁厚为3.5 mm,长为3.5~5 m,排距为2 m。注浆压力为4 MPa。
底板注浆和注浆锚管施工时,为了防止底板跑浆,先在底板上施作一层厚 50 mm、强度等级为C20的水泥砂浆止浆层,24 h后方可注浆。
(5)在底板中线两侧向外1.4 m对称施作两根φ22 mm,L=6.3 m锚索,起抗隆起作用。
新支护方案的数值计算模型如图12所示。新支护方案的支护形式及规格参数见表2。
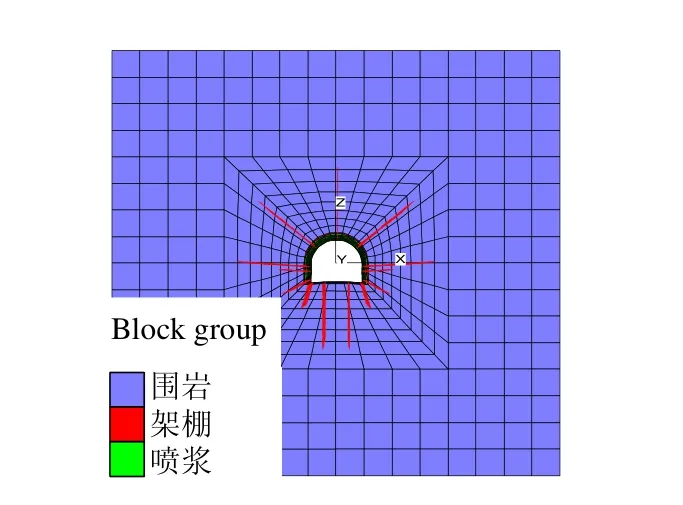
图12 新支护方案模型图Fig.12 New supporting model

表2 新支护形式及规格参数Table 2 New supporting materials and specifications
计算结果如图13所示。
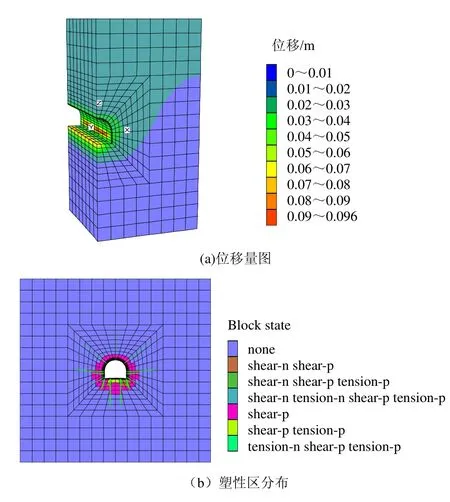
图13 新支护方案计算结果Fig.13 Computational results of the new support
图11与图13比较表明,采取新支护方案后围岩变形量和塑性区范围明显较小,围岩变形得到了有效的控制。
5 现场监测数据
轨道大巷新开挖段采用新支护方案后重新设置了3个测站,监测数据如图14、15所示。
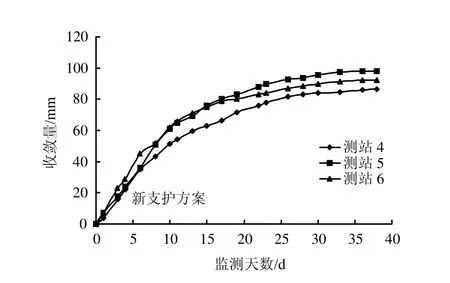
图14 轨道大巷帮部收敛趋势图Fig.14 Convergence magnitude of walls

图15 轨道大巷底臌量趋势图Fig.15 Displacement curves of roadway floor
图14、15监测趋势图表明,在采取新支护方案后变形速率明显降低,并在较短时间内围岩变形趋于收敛,表明所提出的新支护方案取得了良好的效果。
6 结 论
(1)-885 m东翼轨道大巷围岩变形等级为非常严重挤压性大变形,且具有一定的流变特性,在Hoek-Brown弹塑性模型结果上得出了围岩位移解析解。花斑泥岩具有遇水膨胀特性,导致围岩膨胀大变形失稳或干裂疏松破坏失稳。
(2)直墙半圆拱形巷道其肩窝和底角处剪应力集中,高应力与低强度的矛盾更加突出。
(3)围岩经受巷道群二次开挖扰动区和二次应力场叠加影响严重,极其不稳定。
巷道开挖后肩窝和帮角处为剪应力集中区,原支护方案在帮脚和底角部分未进行抗剪支护,且未进行底板支护。因此,针对-885 m轨道大巷提出了新支护方案,特别重视底板支护和底角抗剪支护,数值模拟和现场监测表明,该支护方案取得了良好效果,是一种有效控制深井软岩巷道大变形的支护方法,为该矿及其他矿井类似巷道支护提供了借鉴经验。
[1] 何满潮. 深部的概念体系及工程评价指标[J]. 岩石力学与工程学报, 2005, 24(16): 2853-2858.HE Man-chao. Conception system and evaluation indexes for deep engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(16): 2853-2858.
[2] 钱七虎. 深部地下工空间开发中的关键科学问题[C]//第 230次香山科学会议——深部地下空间开发中的基础研究关键技术问题. [S.l.]: [s.n], 2004: 6-28.
[3] 何满潮, 谢和平, 彭苏萍, 等. 深部开采岩体力学研究[J]. 岩石力学与工程学报, 2005, 24(16): 2803-2813.HE Man-chao, XIE He-ping, PENG Su-ping, et al. Study of rock mechanics in deep mining engineering[J].Chinese Journal of Rock Mechanics and Engineering,2005, 24(16): 2803-2813.
[4] AYDAN O, AKAGI T, KAWAMOTO T. The squeezing potential of rocks around tunnels: Theory and prediction[J]. Rock Mechanics and Rock Engineering,1993, 26(2): 137-163.
[5] ANAGNOSTOU G. A model for swelling rock in tunneling[J]. Rock Mechanics and Rock Engineering,1993, 26(4): 307-331.
[6] HOEK E. Big tunnels in bad rock[J]. Journal of Geotechnical and Geoenvironmental Engineering,2001, 127(9): 726–740.
[7] 刘泉声, 张华, 林涛. 煤矿深部岩巷围岩稳定与支护对策[J]. 岩石力学与工程学报, 2004, 23(21): 3732-3737.LIU Quan-sheng, ZHANG Hua, LIN Tao. Study of stability of deep rock roadways in coal mines and their support measures[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(21): 3732-3737.
[8] SHARAN S K. Elastic-brittle-plastic analysis of circular openings in Hoek-Brown media[J]. International Journal of Rock Mechanics & Mining Sciences, 2003,40(6): 817-824.
[9] PARKA Kyung-ho, KIM Yong-jin. Analytical solution for a circular opening in an elastic-brittle-plastic rock[J].International Journal of Rock Mechanics & Mining Sciences, 2006, 43(4): 616-622.
[10] SHARAN S K. Exact and approximate solutions for displacements around circular openings in elasticbrittle-plastic Hoek-Brown rock[J]. International Journal of Rock Mechanics & Mining Sciences, 2005,42(4): 542-549.
[11] 陈子荫. 围岩力学分析中的解析方法[M]. 北京: 煤炭工业出版社, 1994.
[12] 姜耀东,陆士良. 巷道底臌机理的研究[J]. 煤炭学报,1994, 19(4): 343-351.JIANG Yao-dong, LU Shi-liang. Investigation of mechanism of floor heave of roadway[J]. Journal of China Coal Society, 1994, 19(4): 343-351.

