岩石节理在固定法向压力刚度条件下的剪切理论研究
史 玲,蔡美峰
(1. 北京科技大学 土木与环境工程学院,北京 100083;2. 北京科技大学 金属矿山高效开采与安全教育部重点实验室,北京 100083)
1 引 言
CNS(constant normal stiffness)剪切试验是指试件在剪切过程中,存在一固定法向刚度Kn,所施加的法向压应力随着法向剪胀位移的变化而变化。Goodman通过试验及图解方式说明了岩块在滑落过程中,若通过不断施加法向压力限制其剪胀为0,节理在剪切过程中就会需要更大的剪力[1]。
这一节理剪切状态通常出现在地下巷道围岩中松散岩体的下滑过程。此时若要使岩石滑落首先要使石块在滑落过程中具备足够的剪胀空间,否则因为周围岩块的法向位移限制,而使节理摩擦阻力增大,岩石要想滑落,所需下滑主动力也相应增大。
目前对节理在 CNS条件下的剪切研究主要以试验为主,根据试验结果提出半经验强度公式[2-3]。理论上主要根据Goodman的图解法,提出法向位移方向的剪切刚度 kns、剪切位移方向的法向刚度 ksn来预测CNS剪切过程[4-6]。但这一方法较为复杂,不易理解。本文从剪切过程中法向剪胀位移与剪切位移的关系出发,将该问题简化成一个简单的物理模型,并假设最大剪切应力与残余剪切应力出现时的剪切位移为定值,根据模型中块体相对位移不变,算出某剪切位移条件下的压应力值与剪切应力值,通过不断的循环迭代得到整个过程的剪切应力变化曲线。
2 节理在CNS条件下的剪切模型
2.1 基本假设
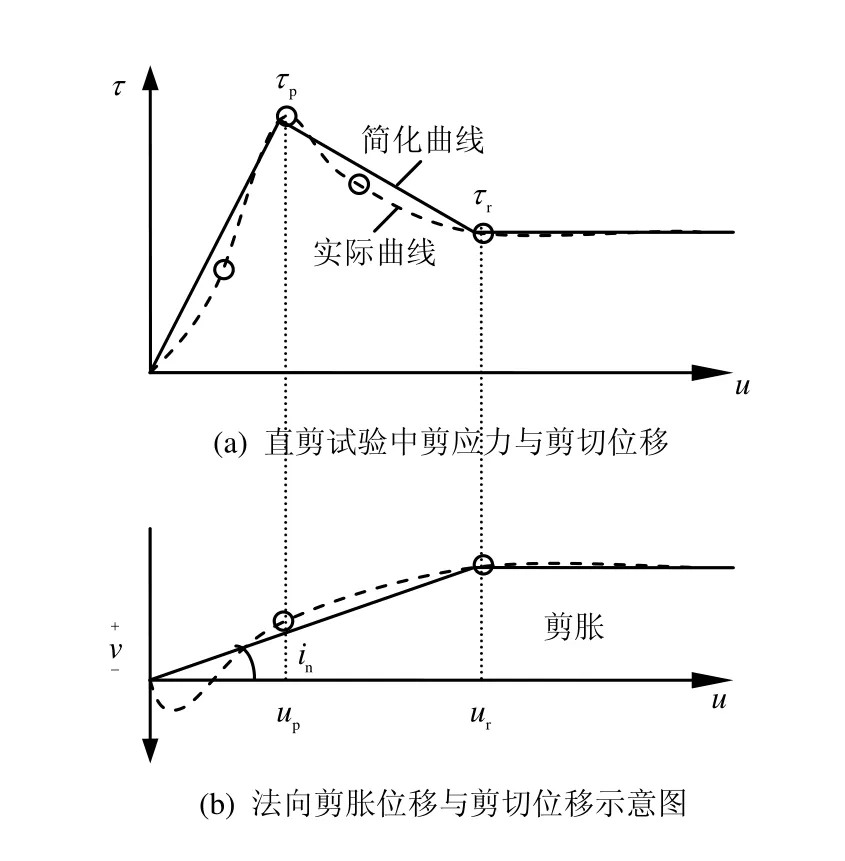
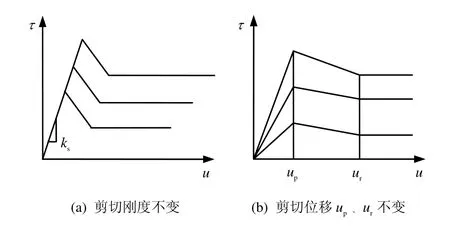
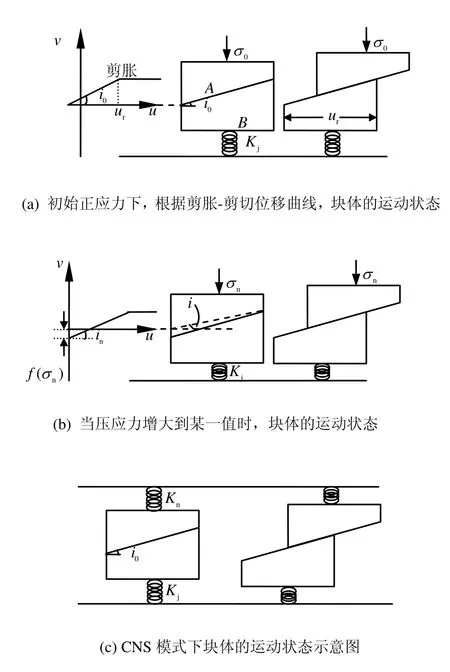
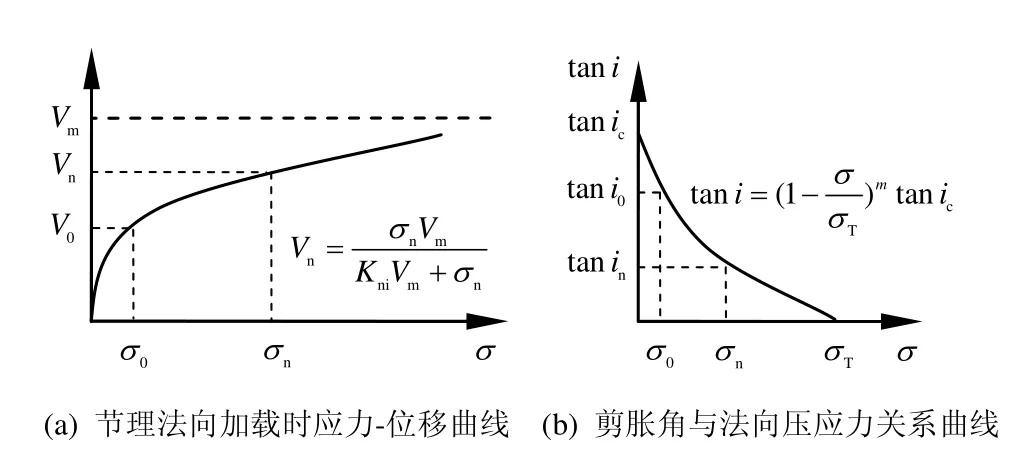
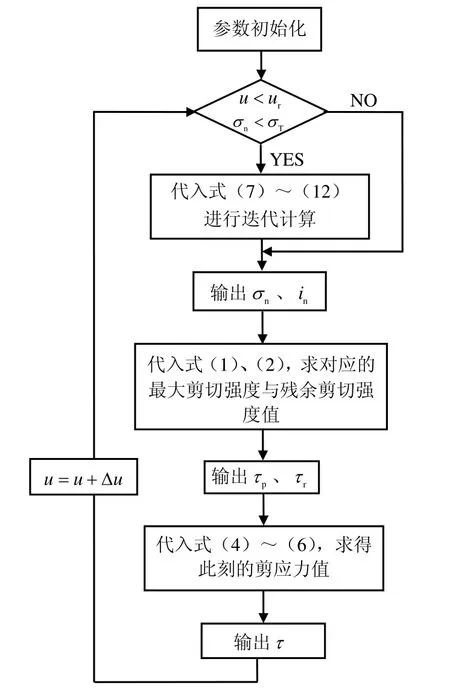
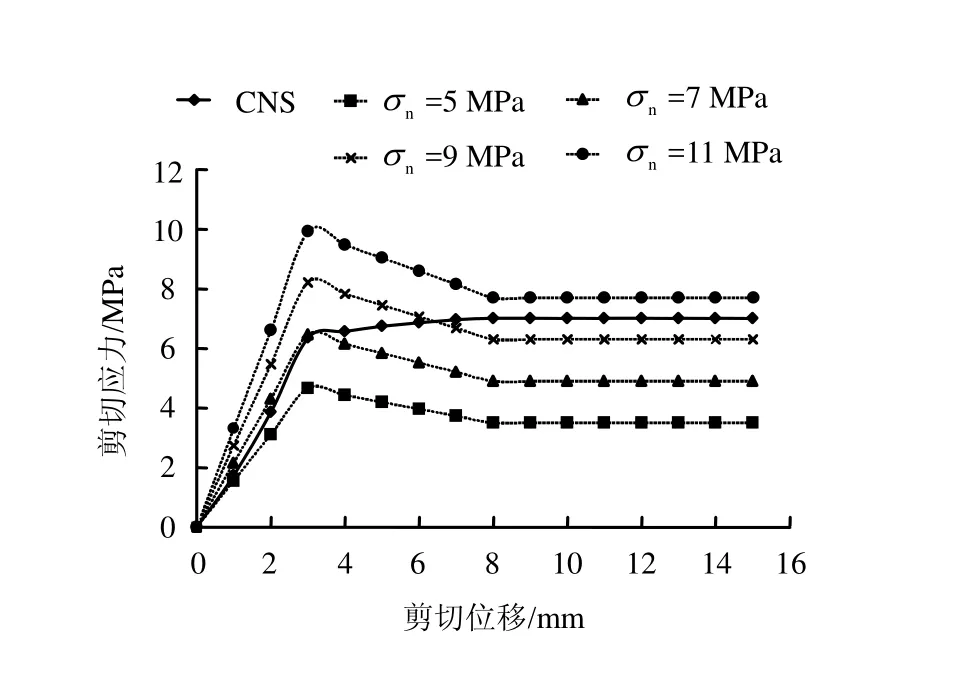
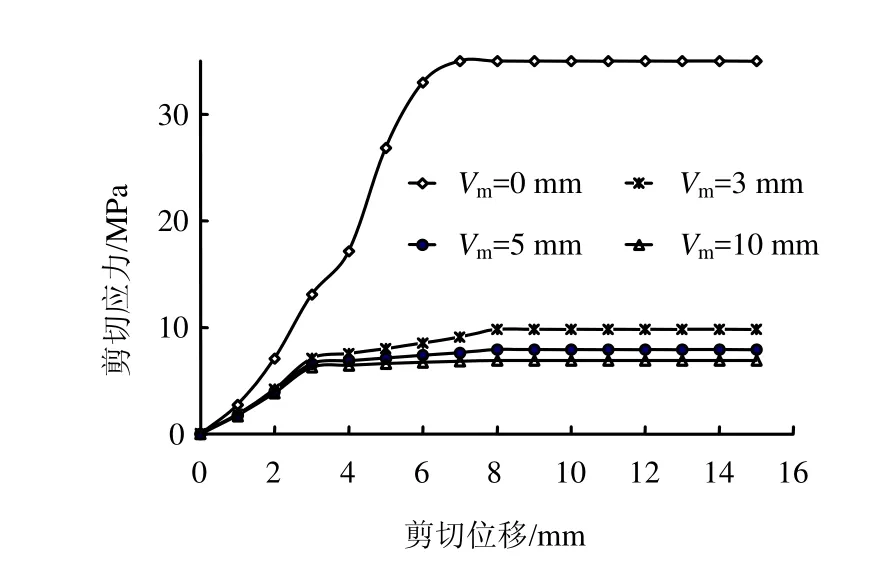
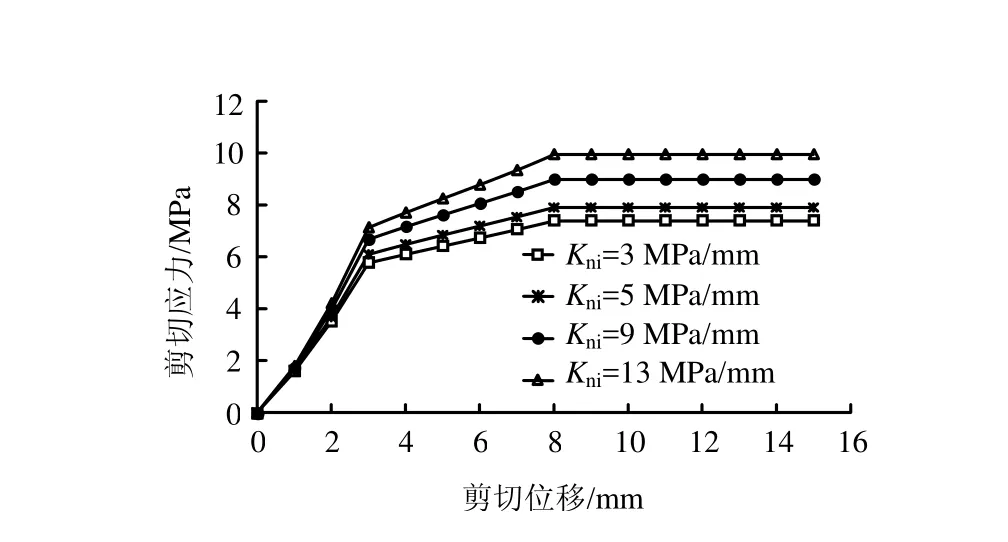
根据大量的试验结果[4],普通直剪试验所得曲线如图1所示,对于剪切应力与剪切位移关系曲线,当剪切位移u从0增大到up时,假设剪切应力线性增大到τp,当up 式中:c为节理凝聚力;σn为法向压应力;φ为节理基础摩擦角;in为剪胀角。 图1 普通直剪试验曲线Fig.1 Curves of ordinary direct shear test 对于不同法向压应力下的直剪试验曲线,一般有两种形式[4],如图2所示:一种是剪切刚度不变,即ks为定值,剪切应力表达式为 另一种是剪切应力达到最大值和残余强度时的剪切位移不变,即up、ur为定值,此过程中剪切应力表达式为 式中:u为剪切位移;up为达到最大剪切应力时的位移;ur为达到残余强度时的位移。 第1种形式计算过程相对简单,很多软件在处理节理强度问题时都采用此种形式;第2种形式较第 1种形式更能真实反映大量试验数据结果,Goodman[1]、Seab[4]在研究CNS剪切过程中均采用此种形式。因此,本文也用第2种形式来进行计算。 图2 不同压应力下剪切应力与剪切位移曲线形式Fig.2 Curves of shear stress vs. shear displacement 根据图1剪切过程中法向位移与剪切位移的关系简化曲线,本文采用两块相配的楔形体的相对运动来表示,如图3所示。 图3(a)中,对于初始压应力σ0,剪胀角为i0,直剪试验中剪胀曲线的变化可以由块体A以倾角i0沿块体B运动过程来表示,楔形体宽度为ur。若压应力增大为σn,如图3(b)所示,假设在剪切过程中,均先施加压力再施加剪力,由于弹簧Kj,块体B会下降一段距离,相对于图3(a),剪胀角减小为i,但块体A和B的相对运动角度仍为i0。Kj表示的是节理在剪切过程中因法向压应力增大而使法向位移减小的状况,包括节理的法向压缩与剪胀角的磨损,很明显Kj不是定值,这将在2.3节中讨论。 因此,对于CNS条件下的剪切过程,在块体A上加一弹簧 Kn即可控制法向压应力的变化,如图3(c)所示。若CNS剪切试验时所施加的初始压应力为σ0,初始剪胀角为i0,则在任意状态(u 当u>ur时,法向压应力保持不变。 式中:σ0为初始压应力;i0为初始剪胀角;Kn为控制压应力的法向刚度;Kj为控制节理法向变形的刚度,此处应为绝对值。 将式(7)代入式(1)~(4)即可得到该时刻剪切应力的值。 图3 楔形块体模拟剪切过程示意图Fig.3 Sketches of wedge block simulating shear progress CNS试验式(4)~(7)中,初始压应力σ0、i0、up、ur、Kn为定值。但对于Kj,它表示压应力增大使得剪切过程中节理法向剪胀位移减小的变化。由图3(b)可以看出,节理剪胀法向位移由两部分组成,一是单纯的节理法向位移随着压应力的增大而减小量f(σn):另一部分表示剪切过程中由于节理齿的磨损 f(in),剪胀角由i0减小为in。故总的法向位移可以表示为 式(8)中节理法向单调加载本构关系 f(σn)项由于接触结构面的强度性质和接触状态,存在不同的经验公式[1,7-9]。此处采用 Bandis的双曲模型来代入计算[9]。将σ0定为初始压应力,如图4(a)所示,则其关系式可写为 式中:Vm为节理的最大闭合位移;Kni为双曲线模型中的最初斜率,此处假设为常数。 图4 不同法向压应力下节理法向位移与剪胀角变化曲线Fig.4 Variation curves of normal displacement and dilatancy angle (tangent value) with different normal compressive stresses 同理,式(8)中剪胀角的磨损项,根据Ladanyi和Archambault得出的经验公式[10],也引入初始压应力σ0和初始剪胀角i0,则由剪胀角引起的法向位移变化可写为 式中:σT为节理在直剪过程中不发生剪胀现象时的最大压应力;m为系数,一般情况下,m=4。 将式(10)、(11)代入式(9),同时使Kj取正值得: 将式(12)代入式(7),即可用迭代法解得压应力与剪切位移在CNS剪切条件下的关系式,得到σn,进而可得到剪切应力与剪切位移的关系。注意当 σ0=σT时,式(11)不成立,此时初始剪胀角i0=0,无剪胀,为Kn=0的情况。且在CNS剪切过程中,可能出现 σn=σT的情况,这时剪胀角的磨损量即为初始剪胀角,也无剪胀,故在迭代计算时要考虑σn(包括σ0)与σT的关系。计算流程如图5所示。 图5 计算流程图Fig.5 Flow chart of calculation 取初始值如表 1所示,设所有应力单位均为MPa,刚度单位为 MPa/mm,位移单位为 mm,位移变量u从0到15,所得结果如图6所示。 表1 初始参数Table 1 Initial values 图6 节理在CNS条件下的剪切应力曲线Fig.6 Shear stress vs. shear displacement curves under CNS conditions 由计算得 CNS剪切过程中压应力的变化从5 MPa到10 MPa左右,故在图6中分别画出压应力为5~11 MPa时直剪状态(CNL)下的剪切应力曲线。通过对比可得,初始压应力为5 MPa时,CNS条件下剪切应力随着剪切位移的增大而增加,其值明显大于压应力5 MPa时CNL条件下的剪切应力值。而且在此算例中,与CNL直剪曲线相比,CNS的剪切应力曲线没有明显的衰减过程,到达最大强度后,几乎一直保持该强度到最后。因此,在CNS条件下,剪切应力曲线更加平缓。 由式(7)得 CNS条件下压应力的变化由 Kn与 Kj协调控制,Kn的确定较为简单,而 Kj的取值则较为复杂。决定Kj取值的式(10)与式(11)中的参数值不仅与岩石强度有关,还与节理风化程度、接触状态、节理粗糙度及实验室试验条件有关,其值存在很大的离散性。大量试验数据显示,即使同一种岩石,试验所得节理强度参数也不尽相同[11]。 为简单计,本文只讨论式(7)与式(12)中参数单独变化时的剪切应力曲线。 初始压应力仍为5 MPa,对于Kn值,分别取2、10、50、500 MPa/mm,其他参数同表1中所列,所得剪切应力曲线如图 7所示。当 Kn很小时(图中Kn=2 MPa/mm曲线),其变化趋势类似于CNL条件下的剪切应力曲线,随着Kn的增加,其曲线逐渐变的平滑。当Kn无限大时,通过式(7)可得,压应力变化由Kn与 Kj相互协调控制,在此情况下其压应力增量则取决于 Kj(Kj此处可看为定值),故其剪切应力曲线随着Kn的无限增大而趋于稳定。 图7 不同Kn条件下CNS剪切应力曲线Fig.7 Shear stress vs. shear displacement curves under CNS conditions with different values of Kn 取不同的Vm值0、3、5、10 mm,其余参数保持不变,所得结果如图8所示。当Vm=0 mm 时,不存在式(10)代表的节理法向变形,剪切过程中只有剪胀角的磨损。因为只存在剪胀,所引起的压应力值较大,故剪切应力值也较大。随着Vm的增加,缓解了法向的变形,剪切应力值逐渐减小。 图8 不同Vm条件下CNS剪切应力曲线Fig.8 Shear stress vs. shear displacement curves under CNS conditions with different values of Vm 当 σn=σT时,式(11)所代表的变形为-u tani0,此时剪胀角的磨损量为原剪胀角,即不存在剪胀。同理当 σn>σT时,剪切过程中也不存在剪胀,法向压应力维持不变,且此时因为剪胀角为 0,最大剪切应力值同残余剪切应力值。故参考表1中相关数值,取不同的σT值分别为2、5、10、50 MPa,其余参数保持不变,结果如图9所示。由图9可看出,随着σT的增加,其剪切应力也逐渐增大。 当σT=2 MPa与σT=5 MPa时,因为初始压应力σ0=5 MPa,剪切过程中不存在剪胀,最大剪切应力值与残余剪切应力值相同,且两条曲线重合,如图9所示。对于图中σT=10 MPa的曲线,其剪切应力在从剪切位移约为5 mm时即维持不变。这表明在CNS剪切过程中,在剪切位移为5 mm附近,压应力 σn≥ σT,剪胀角为0,此后将不在发生剪胀,法向压应力保持不变。 图9 不同σT条件下CNS剪切应力曲线Fig.9 Shear stress vs. shear displacement curves under CNS conditions with different values of σT 表1中,取不同的Kni值3、5、9、13 MPa/mm,其余参数保持不变,得到的结果如图 10所示,Kni值越大,其剪切应力强度越大。Kni表示式(10)双曲线的最初斜率,其数值越大,表示节理越不易压缩,它与Vm的作用相反。 图10 不同Kni条件下CNS剪切应力曲线Fig.10 Shear stress vs. shear displacement curves under CNS conditions with different values of Kni 本文以节理剪切过程中法向剪胀位移与剪切位移的关系为基础,通过一个楔形物理模型来模拟节理在CNS条件下的剪切过程,同时讨论了节理主要参数对CNS剪切曲线的影响。 (1)增大法向压应力刚度Kn,其CNS剪切强度也增大,但并不是无限增大,而是随着Kn的增加而趋于稳定。 (2)对于影响节理法向变形的参数(包括单轴压缩变形及剪胀角的磨损),其值的改变所引起的剪切应力变化规律表现为,节理在剪切过程中越不易发生压缩变形,其剪切应力值也就越大。 所提出的计算模型能准确的预测节理在 CNS条件下的剪切过程,使得研究各参数的影响变得更加容易,为以后的研究奠定基础。 [1] GOODMAN R E. Introduction to rock mechanics[M].New York: John Wiley & Sons, 1989. [2] INDRARATNA B, HAQUE A, AZIZ N. Laboratory modeling of shear behaviour of soft joints under constant normal stiffness condition[J]. Geotechnical & Geological Engineering, 1998, 16: 17-44. [3] JIANG Y, XIAO J, TANABASHI Y, et al. Development of an automated servo-controlled direct shear apparatus applying a constant normal stiffness condition[J].International Journal of Rock Mechanics and Mining Sciences, 2004, 41(2): 275-286. [4] SEAB S, AMADEI B. Modelling rock joints under shear and normal loading[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1992, 29(3): 267-278. [5] SEIDEL J P, HABERFIELD C M. A theoretical model for rock joints subjected to constant normal stiffness direct shear[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(5): 539-553. [6] SOULEY M, HOMAND F. Stability of jointed rock masses evaluated by UDEC with an extended Saeb-Amadei constitutive law[J]. International Journal of Rock Mechanics and Mining Sciences &Geomechanics Abstracts, 1996, 33(3): 233-244. [7] 孙广忠. 岩体结构力学[M]. 北京: 科学出版社, 1988. [8] BARTON N, BANDIS S, BAKHTAR K. Strength,deformation and conductivity coupling of rock joints[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1985, 22(3): 121-140. [9] BANDIS S C, LUMSDEN A C, BARTON N R.Fundamentals of rock joint deformation[J]. International Journal of Rock Mechanics and Mining Sciences &Geomechanics Abstracts, 1983, 20(6): 249-268. [10] LADANYI B, ARCHAMBAULT G. Simulation of shear behavior of a jointed rock mass[C]//The 11th U.S.Symposium on Rock mechanics. Berkeley: American Rock Mechanics Association, 1970: 105-125. [11] ZANGERL C, EVANS K F, EBERHARDT E, et al.Normal stiffness of fractures in granitic rock: A compilation of laboratory and in-situ experiments[J].International Journal of Rock Mechanics and Mining Sciences, 2008, 45(8): 1500-1507.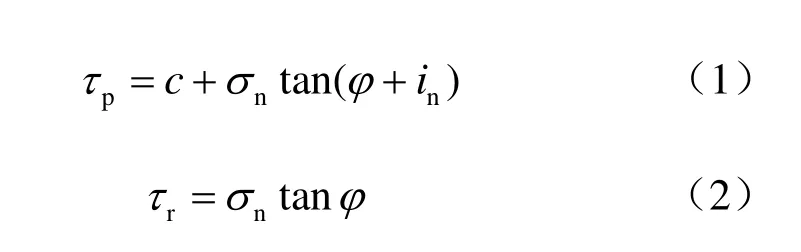

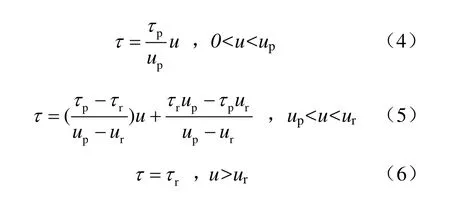
2.2 物理模型的建立
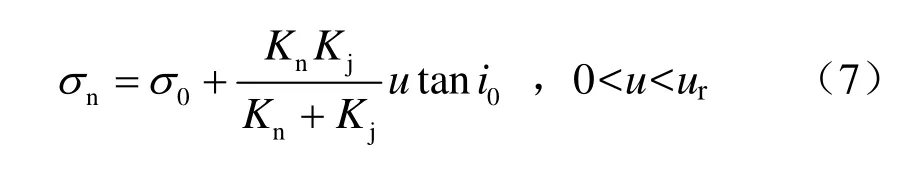
2.3 模型中具体参数确定及运算方法
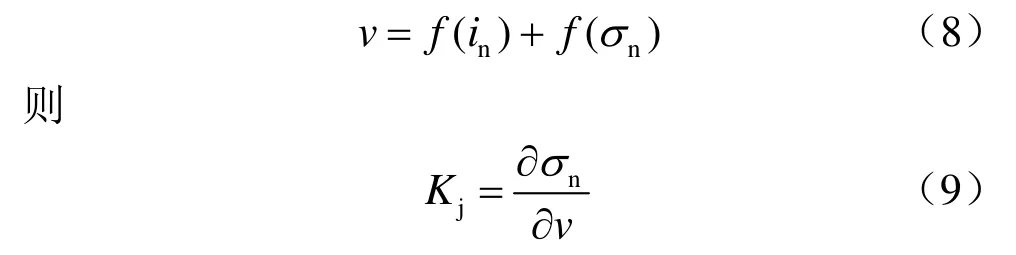
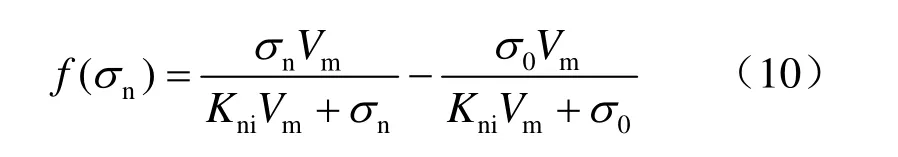


3 算例及各参数影响

3.1 不同Kn条件下的CNS剪切应力变化

3.2 不同Vm条件下的CNS剪切应力变化
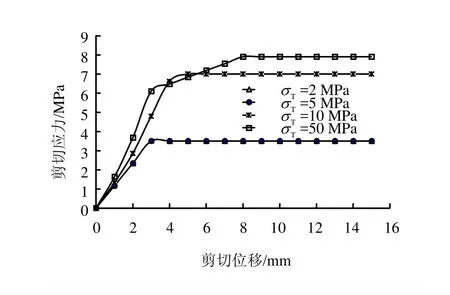
3.3 不同σT条件下的CNS剪切应力变化
3.4 不同Kni条件下的CNS剪切应力变化
4 结 论

