透壁通风管路堤的对流换热和蒸发散热

孙斌祥，杨丽君，王 伟，章金钊，汪双杰

（1. 绍兴文理学院 土木工程系，浙江 绍兴 312000；2. 中交第一公路勘察设计研究院有限公司多年冻土区公路建设与养护技术交通行业重点实验室，西安 710075）

1 引 言

为了应对全球气候变暖、施工和营运等多种因素对青藏公路沿线多年冻土造成的不利影响，规划中的青藏高速公路建设需要采用主动调节和控制地温的冷却路基新技术[1－4]，使得路堤及以下土层减少融化，保持冻结，抑制冻土层的退化甚至冻土层有所加厚，从而达到工程安全运营的目的[1－3]。这些技术主要利用了冬季自然对流或强迫对流降温效应，包括块（碎）石路堤[3－6]、通风管路堤[7－25]、热管[12]、旱桥和遮阳棚技术[1]等，有许多已应用于青藏铁路工程的建设之中。但青藏高原的高海拔多年冻土地区年平均气压低、空气稀薄，单纯由块石路堤、护坡中空气密度不均匀引起的冬季自然对流降温效应也会减弱很多[3－4]，并且路堤全部采用块石填筑会造成取料困难和增加工程造价。另外，气象观察资料也显示青藏公路所经过的多年冻土区的风速很大，低气温期间的风速比高气温期间的风速要大[26－29]，可见，采用综合性的地温调控技术将更能充分地利用冬季冷空气来降低路基及其下土层的温度[9, 15－25]。

国内有关通风管路基的理论分析、室内试验和现场试验已做了许多有益的探索[7－15]，通过加装温控门可控制通风管只在冬季通风[24－25]，在通风管口加装能自然迎风的采风口将能更高效利用冷空气的对流来增强通风管对路基的降温效果[18－20]。针对透壁通风管公路路堤，室内试验[18－19]和青藏高原现场试验[16－17]都表明，在管壁增加透气小孔能增强路基土层的水分蒸发，这既增强了路基降温的效果，也有利于土层保持干燥而使路基稳定。在青藏公路高速化改建的背景下，本文对透壁通风管管壁由于水分蒸发而产生的蒸发散热进行了定量研究，以便于在实际工程应用中对透壁通风管路堤水分蒸发散热降温效应的理论分析。

2 透壁通风管对流换热和蒸发散热

根据室内外试验研究[16－19]，透壁通风管路堤中透壁通风管主要以管壁与空气之间的对流换热和土体水分通过管壁小孔的蒸发散热两种热交换方式强化冻土路堤的降温效果。

2.1 管壁与空气之间的对流换热

管壁与管内空气的对流换热是多年冻土区通风管路堤与外界空气发生热交换的重要形式，对流换热量的大小将直接影响通风管路堤的降温效果。通风管与低温空气进行对流换热能够冷却路堤及其下面的土层[7－10,14－19]，但通风管与暖空气之间的对流换热将会加热路堤及其下面的土层[24－25]。对于通风管管壁的对流换热，属于第3类边界条件，有[7－9]

式中：qt为通风管管壁与空气之间的对流换热热流密度；αt为通风管管壁与空气之间的有效对流换热系数；λ0为管壁的有效导热系数；θ为管壁温度；θa1为通风管内的空气温度；n为管壁边界外法线方向。

图1所示为透壁通风管壁面，任取管壁面积单元d A，其中，透壁小孔所占面积为dAp，管壁实体面积为 dAd，显然d A=dAd+dAp成立，则透壁通风管壁面的开孔率np可定义为

由于透壁通风管壁面小孔部分的面积实际为路堤填土占据，所以整个壁面由通风管未开孔部分壁面和开孔部分填土表面两种材料表面组成，假设局部热平衡条件成立，则两种材料都能满足式（1）表示的对流换热边界条件，对它们求面积单元 dA的平均值[30]，得到考虑透壁通风管壁面开孔的管壁与空气之间对流换热边界条件，其形式上与式（1）相同，但有效导热系数λ0及有效对流换热系数αt具体表示为

式中：λd、αt分别为通风管组成材料的导热系数和对流换热系数；λs和αs分别为通风管附近路堤填土的导热系数和对流换热系数；开孔率np以小数计。

图1 透壁通风管小孔布置Fig.1 Distribution of small holes in a perforated ventilation pipe

文献[7－9]为了简化而在通风管路堤传热分析中取对流换热系数为15 W/(m2·K)，可是通风管材料性质、风速等因素都会对管壁对流换热系数产生影响[31－32]，因此，在分析通风管路堤对流换热时全面考虑这些因素的影响显得尤为重要。由于实际通风管路堤一般采用混凝土管，且通风管内空气流动速度一般小于5 m/s，其对流换热系数可采用文献[31]计算公式，所以考虑风速等因素影响的透壁通风管混凝土管壁部分的对流换热系数可表示为[31]

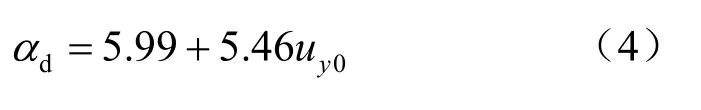
式中：uy0为通风管轴线方向的空气流动速度。而考虑风速等因素影响的土体部分的对流换热系数可表示为[31]

2.2 透壁通风管蒸发散热

2.2.1 蒸发散热边界条件

由于少量的水分蒸发需要消耗大量的热量，所以水分蒸发能显著降低路堤土体的温度[26－28,33]。土体水分蒸发速率除与空气的温度和湿度有关外，也与空气流动速度密切相关，另外，还与路堤填料物理性质等因素有关[34－39]。对于通风管开孔管壁的蒸发散热边界，透壁通风管开孔管壁由水分蒸发散热引起的热流密度qv主要由两部分组成，即未开孔部分壁面水分蒸发和开孔部分土体表面水分蒸发。假设通风管管壁未开孔部分壁面和开孔部分土体表面单位面积的水分蒸发质量流量分别为md和ms，且水分蒸发满足局部热平衡及准稳态条件，则透壁通风管管壁单位面积的总水分蒸发质量流量mv为

由于通风管未开孔部分管壁表面的水分蒸发强度要远小于土体表面的水分蒸发，因此，可以忽略不计未开孔管壁表面的水分蒸发，即md≈0，则透壁通风管管壁考虑水汽化潜热后的水分蒸发散热热流密度可表示为

式中：Lv为水对应于温度θ时的汽化潜热。将蒸发散热等效为牛顿冷却公式的形式[32]，则有

式中：αv为透壁通风管管壁的蒸发散热系数，有

式中：Δθ=θ-θal，为蒸发壁面处和空气间的温度差。

2.2.2 透壁通风管管壁蒸发散热系数

根据文献[32]，一般潮湿土表面的水分蒸发质量流量ms可用蒸发壁面附近及空气的水蒸汽分压力及相应温度表示为

式中： Pv、Pva分别为蒸发壁面土体和空气中的水蒸汽分压力；Rv=461 J/(kg·K)为水蒸汽的气体常数；ρ和cp为湿空气的密度和定压比热；Le为Lewis准则数，等于湿空气的热扩散系数除以水蒸汽的扩散系数。

利用水蒸汽分压力与饱和水蒸汽分压力关系Pv=φvPvb(θ)及式（10），可由式（9）得到透壁通风管管壁水分蒸发散热系数为

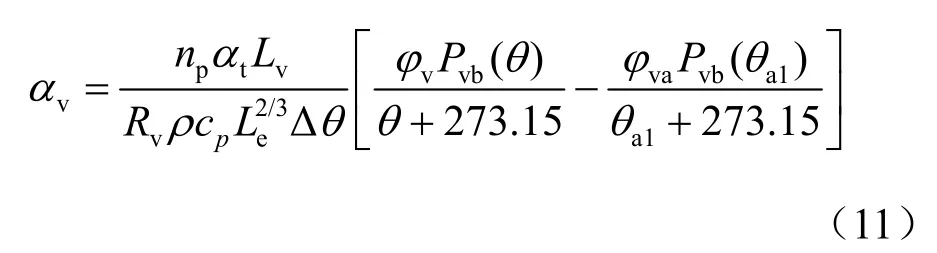
式中：φv和φva分别为蒸发壁面附近土体和空气中的相对湿度，以小数计；Pvb(θ)为饱和水蒸汽分压力随温度的函数关系[40]。从式（11）可知，土体水分蒸发速率除与土体、空气的温度和湿度有关外还与空气流动速度密切相关，其通过有效对流换热系数αt具体体现，当然，其也与透壁通风管管壁开孔率成正比关系。

显然，在利用式（11）计算壁面水分蒸发散热系数时要用到壁面附近土体的相对湿度关系式，根据文献[34－39]，可把蒸发表面附近土体中空气相对湿度与土体含水率联系起来，具体关系式为

式中：φ和φs分别为蒸发壁面附近土体的体积含水率和体积饱和含水率，以小数计；a0、b0及n0分别为路堤土体的材料常数，具体需要由试验确定，对于黏土[36]，φs=0.50，a0=0.018，b0=0.020，n0=2.1。土体基质吸力Ψ与土体相对湿度的关系式为[40]

式中：Ψ的单位为105Pa。

然后，利用土体体积含水率和重量含水率的相关定义[41]，可以得到融土重量含水率w与体积含水率的关系式为

式中：ρs为土体的相对密度；ρd为土体干密度；ρw为纯水密度，取为1.0 g/cm3。

如果不考虑冰的升华，则土体中只有未冻水含量这部分水才产生蒸发散热，因此，式（14）中的含水率w应只是土体的未冻水含量。当土体处于融化状态时，土体含水率全部为未冻水含量，则通风管透壁附近土体中的全部水分是发生蒸发散热的水源；当土体处于冻结状态时，液态水中除大部分转变成固态冰外还有小部分仍然保持液态水即未冻水，则通风管透壁附近土体中只有这部分未冻水含量才是发生蒸发散热的水源。研究表明[41]，土体中未冻水的含量主要取决于土质、外界条件以及冻融历史等3大因素，对于给定冻土，未冻水含量wu与负温绝对值的关系为

式中：a1和b1为土体材料常数，具体计算公式为[41]

式中：w0为土体的初始含水率；θc为土体冻结温度。

2.3 透壁通风管的总换热边界条件

因此，透壁通风管管壁的总热交换应由对流换热和蒸发散热组成，由式（1）和式（8）叠加，可得通风管管壁边界的总换热边界条件为

式中：q为透壁通风管管壁换热的总热流密度，其为对流换热热流密度和蒸发散热热流密度之和。

通常情况下，上述分析中需要用到水分蒸发时的汽化潜热Lv、饱和水蒸汽分压力Pvb(θ)、大气压力Pa、湿空气密度ρa、湿空气定压比热cp以及湿空气含湿量d等计算公式见式（18）～（20）根据道尔顿分压定律可知，大气压力为 P=Pa+Pva，湿空气密度为 ρ=ρa+ρva。

式中：z为海拔高度；Pa0=101320 Pa；cpa和cpv分别为组成一般湿空气的干空气和水蒸汽的定压比热，cpa=1.01 kJ/(kg·K)，cpv=1.84 kJ/(kg·K)；干空气气体常数 Ra=287 J/(kg·K)。

3 水分蒸发散热的影响

根据青藏高原冻土区通风管试验路堤的现场观测结果，对于年平均温度-3.6 ℃及幅度13.5 ℃的气温条件，可回归得到管内空气温度变化规律为[14]

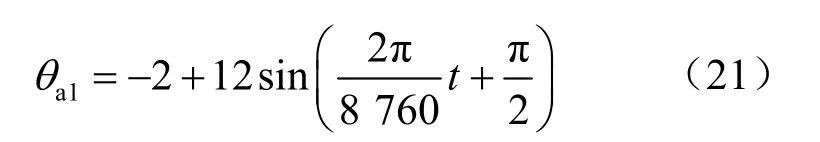
而通风管管壁表面的温度变化规律为[14]

根据青藏高原公路典型路段的风速观察资料以及风速随高度变化的幂指数定理[9]，同时，考虑通风管局部阻力损失及沿程阻力损失的影响，管外风速换算成管内风速要乘以一个阻力系数ξ1，则通风管内轴线处的风速年变化规律可表示为[20]

式中：h1为通风管轴线距天然地表的高度，根据文献[20]方法，计算得阻力系数为ξ1=0.557。另外，根据青藏高原气象观测资料[29]，取通风管内空气的相对湿度按如下规律变化

利用式（3）的对流换热系数αt、式（11）、式（22）～（24），可由式（17）获得通风管管壁对流换热及水分蒸发散热随空气温度、风速、管壁开孔率及路堤填土含水率等变化而变化，图2具体给出了相应热流密度的变化规律，其中，透壁通风管管壁开孔率为40%。由图2可知，管壁的水分蒸发使路堤填土中的部分水分将随通风管中空气运动而带到路堤外面，使路堤产生水分蒸发散热，在10月至次年4月期间，由于冻土层未冻水含量较小，而使路堤通过管壁水分蒸发的散热也较小（散热热流密度在28.2～2.0 W/m2之间变化），路堤总的降温效果主要由管壁对流换热效应控制（这时总散热热流密度在 28.5～47.4 W/m2之间变化），而在 4月至10月期间，虽然通风管内空气与管壁的对流换热效应可使路堤土体增温（吸热热流密度在-25.5～0.3 W/m2之间变化），但同时通过管壁小孔的水分蒸发散热将对路堤产生降温效应（散热热流密度在23.2～41.3 W/m2之间变化），这期间由于通风管周围融土的未冻水含量较大，使得通过管壁小孔的水分蒸发散热也较大,这可以部分或全部抵消对流换热而引起的增温效应（总散热热流密度值在-2.3～35.9 W/m2之间变化），只有6月中旬至7月中旬近1个月时间有弱的增温现象，总体上其有利于减小暖季对流换热效应对路堤的不利影响。上述理论分析结果已由透壁通风管路堤降温效应及水分蒸发散热的室内试验研究所证实[18－19,42]。

图2 对流换热密度、蒸发散热密度及总热流密度之间的关系Fig.2 Relations between convective heat, evaporative heat and total heat flux densities

图3给出了通风管管壁不同开孔率对管壁总换热效应的影响规律。随着管壁开孔率从 0增大至0.4，暖季的水分蒸发散热效应也不断增强，使得抵消暖季管壁对流换热引起的增温效应的能力也不断增强，而冬季的水分蒸发散热效应很小，远小于管壁对流换热产生的降温效应。当np=0时，不开孔通风管路堤在10月至次年4月之间通风管通风才表现出对流降温效果，除此以外的近6个月时间都表现为增温效果；当np=0.1时，透壁通风管路堤在9月中旬至次年4月下旬期间通风管通风表现出对流降温效果，其余近4.5个月时间表现为增温效果；当np=0.2时，透壁通风管路堤在8月下旬至次年5月上旬期间通风管通风都表现出对流降温效果，而增温效果的持续时间约有3.5个月；当np=0.3时，透壁通风管路堤在8月上旬至次年5月下旬期间通风管通风都表现出对流降温效果，表现增温时间约2.5个月；当np=0.4时，透壁通风管路堤在7月中旬至次年6月中旬期间通风管通风都能表现出对流降温效果，只有近1个月的时间表现为增温效果。为了完全消除上述相应时期内的增温现象，还需要结合自动温控门技术来控制透壁通风管的通风时间。理论上，管壁开孔率越大，透壁通风管蒸发散热能力也越强，但从热学、力学稳定性等综合考虑，通风管管壁开孔率取0.35～0.45比较合理。

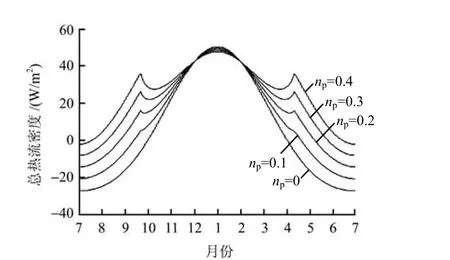
图3 开孔率对管壁换热总热流密度的影响Fig.3 Effect of perforating ratio on total heat flux density through pipe wall

4 结 论

（1）透壁通风管路堤土体的水分可以通过裸露在管壁小孔的土体表面进行蒸发，水分蒸发能带走大量热量而产生蒸发散热，其有利于路堤土体的温度降低。分析发现，路堤透壁通风管主要以管壁与空气的对流换热和土体水分通过管壁小孔的蒸发散热两种方式与周围大气进行热交换。

（2）针对青藏高原冻土区透壁通风管路堤，具体分析了透壁通风管管壁对流换热和水分蒸发散热的影响因素，并给出了透壁通风管管壁对流换热系数和蒸发散热系数随开孔率、风速及含水率等的关系式。

（3）具体计算表明，由于管壁的水分蒸发，路堤填土中的部分水分将随通风管中空气流动而带到路堤外面，使路堤产生蒸发散热，由于土层未冻水含量较小，冬季路堤通过管壁的水分蒸发散热效应也较小，路堤总的降温效果主要由管壁对流换热效应控制，而暖季通风管内空气与管壁的对流换热效应可使路堤土体增温。同时，通过管壁小孔的水分蒸发散热将对路堤产生降温效应，由于通风管周围融土的未冻水含量较大，使得通过管壁小孔的水分蒸发散热效应也较大，这可部分或全部抵消对流换热而引起的增温效应，有利于减小夏季对流换热效应对路堤的不利影响。

[1] CHENG G D, SUN Z Z, NIU F J. Application of the roadbed cooling approach in Qinghai-Tibet Railway engineering[J]. Cold Regions Science and Technology,2008, 53(3): 241－258.

[2] JIN H J, WEI Z, WANG S L, et al. Assessment of frozen-ground conditions for engineering geology along the Qinghai-Tibet highway and railway, China[J].Engineering Geology, 2008, 101(3－4): 96－109.

[3] MA W, SHI C H, WU Q B, et al. Monitoring study of technology of the cooling roadbed in permafrost region of Qinghai-Tibet Plateau[J]. Cold Regions Science and Technology, 2006, 44(1): 1－11.

[4] WU Q B, LU Z J, ZHANG T J, et al. Analysis of cooling effect of crushed rock-based embankment of the Qinghai-Tibet Railway[J]. Cold Regions Science and Technology, 2008, 53(3): 271－282.

[5] SUN B X, YANG L J, XU X Z. Onset and evaluation on winter-time natural convection cooling effectiveness of crushed-rock highway embankment[J]. Cold Regions Science and Technology, 2007, 48(3): 218－231.

[6] SUN B X, YANG L J, LIU Qi, et al. Numerical analysis for critical thickness of crushed rock revetment layer on Qinghai-Tibet Railway[J]. Cold Regions Science and Technology, 2009, 57(2－3): 131－138.

[7] LAI Y M, WANG Q S, NIU F J, et al. Three-dimensional nonlinear analysis for temperature characteristic of ventilated embankment in permafrost regions[J]. Cold Regions Science and Technology, 2004, 38(2－3): 165－184.

[8] 李宁, 苏波, 全晓娟, 等. 冻土通风管路基的温度场分析与设计原则探讨[J]. 土木工程学报, 2005, 38(2): 81－86.LI Ning, SU Bo, QUAN Xiao-juan, et al. Approach on temperature field analysis and design principle of bed for ventilating pipeline in frozen soil[J]. China Civil Engineering Journal, 2005, 38(2): 81－86.

[9] ZHANG M Y, LAI Y M, NIU F J, et al. A numerical model of the coupled heat transfer for duct-ventilated embankment under wind action in cold regions and its application[J]. Cold Regions Science and Technology,2006, 45(2): 103－113.

[10] 蒋武军, 葛修润. 双能量方程在通风路基多孔介质中的应用[J]. 岩石力学与工程学报, 2006, 25(6): 1170－1176.JIANG Wu-jun, GE Xiu-run. Application of doubleenergy equation to porous media of ventilated embankment[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(6): 1170－1176.

[11] 徐学燕, 苏万鑫, 徐春华. 控制冻土融化容许值的建筑物通风管基础计算方法[J]. 土木工程学报, 2006, 39(9):98－102.XU Xue-yan, SU Wan-xin, XU Chun-hua. An approach for computing the ventilated foundation of buildings based on controlling the permissible value of permafrost thawing[J]. China Civil Engineering Journal, 2006,39(9): 98－102.

[12] 刘奉喜, 刘建坤, 郭大华, 等. 多年冻土地区热管冷却路基数值分析[J]. 土木工程学报, 2004, 37(9): 41－47.LIU Feng-xi, LIU Jian-kun, GUO Da-hua, et al.Numerical analysis of thermosyphon in protecting the roadbed in permafrost[J]. China Civil Engineering Journal, 2004, 37(9): 41－47.

[13] 刘志强, 马巍, 周国庆, 等. 纵向布管调控冻土路基温度场的模拟试验研究[J]. 岩石力学与工程学报, 2005,24(11): 1827－1831.LIU Zhi-qiang, MA Wei, ZHOU Guo-qing, et al.Simulated experiment study of the temperature field of frozen subgrade modulated by horizontal pipes[J].Chinese Journal of Rock Mechanics and Engineering,2005, 24(11): 1827－1831.

[14] NIU F J, LIU X F, MA W, et al. Monitoring study of the boundary thermal conditions of duct-ventilated embankment in permafrost regions[J]. Cold Regions Science and Technology, 2008, 53(3): 305－316.

[15] ZHANG M Y, LAI Y M, Dong Y H, et al. Laboratory investigation on cooling effect of duct-ventilated embankment with a chimney in permafrost regions[J].Cold Regions Science and Technology, 2008, 54(2): 115－119.

[16] 胡明鉴, 汪稔, 葛修润, 等. 透壁通风管对青藏铁路路基的冷却效果试验初探[J]. 岩石力学与工程学报, 2004,23(24): 4195－4199.HU Ming-jian, WANG Ren, GE Xiu-run, et al. An experimental study of cooling effect of the perforated ventilation pipes on Qinghai-Tibet Railway Roadbed[J].Chinese Journal of Rock Mechanics and Engineering,2004, 23(24): 4195－4199.

[17] 胡明鉴, 汪稔, 孔令伟, 等. 青藏铁路透壁通风管通风路基模型试验及初始温度场特征[J]. 冰川冻土, 2004,26(5): 582－586.HU Ming-jian, WANG Ren, KONG Ling-wei, et al.Simulated experiment of the embankment with perforated ventilation pipes and the features of its initial temperature field of the Qinghai-Tibet Railway[J]. Journal of Glaciology and Geocryology, 2004, 26(5): 582－586.

[18] 刘琦, 孙斌祥, 徐学祖, 等. 透壁通风管路堤降温效应的室内试验研究[J]. 岩土工程学报, 2006, 28(9): 1153－1158.LIU Qi, SUN Bin-xiang, XU Xue-zu, et al. Investigation of laboratory test on cooling effect of embankment with perforated ventilation pipe[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9): 1153－1158.

[19] 刘琦, 孙斌祥, 杨丽君, 等. 透壁通风管路堤的降温特性研究[J]. 岩土工程学报, 2008, 30(8): 1152－1157.LIU Qi, SUN Bin-xiang, YANG Li-jun, et al. Cooling effect of embankment with perforated ventilation pipe[J].Chinese Journal of Geotechnical Engineering, 2008,30(8): 1152－1157.

[20] 杨丽君, 孙斌祥, 王伟, 等. 寒区路堤通风管的自然通风能力研究[J]. 中国公路学报, 2008, 21(4): 25－29.YANG Li-jun, SUN Bin-xiang, WANG Wei, et al. Natural ventilation characteristics of ventilation pipe in ventilated embankment in permafrost regions[J]. China Journal of Highway and Transport, 2008, 21(4): 25－29.

[21] CHATAIGNER Y, GOSSELIN L, DORÉ G. Optimization of embedded inclined open-ended channel in natural convection used as heat drain[J]. International Journal of Thermal Sciences, 2009, 48(6): 1151－1160.

[22] JØRGENSEN A S, DORÉ G, VOYER É, et al.Optimization of the characteristics of two heat removal techniques for permafrost protection[J]. Cold Regions Science and Technology, 2008, 53(2): 179－192.

[23] XU J, GOERING D J. Experimental validation of passive permafrost cooling systems[J]. Cold Regions Science and Technology, 2008, 53(3): 283－297.

[24] YU Q H, SHI C H, NIU F J, et al. Analysis of temperature controlled ventilated embankment[J]. Cold Regions Science and Technology, 2005, 42(1): 17－24.

[25] 李国玉, 李宁, 全晓娟. 可调控通风管路基的降温效果[J]. 岩石力学与工程学报, 2005, 24(18): 3287－3291.LI Guo-yu, LI Ning, QUAN Xiao-juan. Cooling effect on adjustable ventilated embankment[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(18): 3287－3291.

[26] YAO J M, ZHAO L, DING Y J, et al. The surface energy budget and evapotranspiration in the Tanggula region on the Tibetan Plateau[J]. Cold Regions Science and Technology, 2008, 52(3): 326－340.

[27] 陈继, 盛煜, 程国栋. 从地表能量平衡各分量特点论青藏高原多年冻土工程中的冻土保护措施[J]. 冰川冻土,2006, 28(2): 223－228.CHEN Ji, SHENG Yu, CHENG Guo-dong. Discussion on protection measures of permafrost under the action of engineering from the point of earth surface energy balance equation in Qinghai-Tibetan Plateau[J]. Journal of Glaciology and Geocryology, 2006, 28(2): 223－228.

[28] 陈继, 程国栋, 吴青柏, 等. 冻土地区风的作用分析——以青藏铁路线多年冻土为例[J]. 地球科学进展,2005, 20(3): 275－281.CHEN Ji, CHENG Guo-dong, WU Qing-bai, et al. Wind’s cooling effect on frozen soil—For example of Qinghai-Tibet Railway[J]. Advances in Earth Science, 2005, 20(3): 275－281.

[29] 张世强, 丁永建, 卢健, 等. 青藏高原土壤水热过程模拟研究(I): 土壤湿度[J]. 冰川冻土, 2004, 26(4): 384－388.ZHANG Shi-qiang, DING Yong-jian, LU Jian, et al.Simulative study of water-heat process in the Tibetan Plateau(I): Soil moisture[J]. Journal of Glaciology and Geocryology, 2004, 26(4): 384－388.

[30] NIELD D A, BEJAN A. Convection in porous media[M].New York: Springer-Verlag, 1999.

[31] 张建荣, 刘照球. 混凝土对流换热系数的风洞实验研究[J]. 土木工程学报, 2006, 39(9): 39－42.ZHANG Jian-rong, LIU Zhao-qiu. A study of the convective heat transfer coefficient of concrete in wind tunnel experiment[J]. China Civil Engineering Journal,2006, 39(9): 39－42.

[32] 刘艳峰, 刘加平. 建筑外壁面换热系数分析[J]. 西安建筑科技大学学报(自然科学版), 2008, 40(3): 407－412.LIU Yan-feng, LIU Jia-ping. Study of heat transfer coefficient at exterior building surface[J]. Journal of Xi’an University of Architecture & Technology(Natural Science Edition), 2008, 40(3): 407－412.

[33] KANE D L, HINKEL K M, GOERING D J, et al. Nonconductive heat transfer associated with frozen soils[J].Global and Planetary Change, 2001, 29(3－4): 275－292.

[34] WANPHEN S, NAGANO K. Experimental study of the performance of porous materials to moderate the roof surface temperature by its evaporative cooling effect[J].Building and Environment, 2009, 44(2): 338－351.

[35] 杨洋, 姚海林, 卢正. 蒸发条件下路基对气候变化的响应模型及影响因素分析[J]. 岩土力学, 2009, 30(5):1209－1214.YANG Yang, YAO Hai-lin, LU Zheng. Model of subgrade soil responding to change of atmosphere under evaporation and its influential factors[J]. Rock and Soil Mechanics, 2009, 30(5): 1209－1214.

[36] 魏宁, 茜平一, 傅旭东. 降雨和蒸发对土质边坡稳定性的影响[J]. 岩土力学, 2006, 27(5): 778－781.Wei Ning, Qian Ping-yi, Fu Xu-dong. Effects of rainfall infiltration and evaporation on soil slope stability[J].Rock and Soil Mechanics, 2006, 27(5): 778－781.

[37] 夏卫生, 雷廷武, 杨文治, 等. 蒸发条件下土壤水分再分布的动力学研究[J]. 水利学报, 2002, (7): 37－41.XIA Wei-sheng, LEI Ting-wu, YANG Wen-zhi, et al.Dynamics of soil water redistribution during evaporation[J].Journal of Hydraulic Engineering, 2002, (7): 37－41.

[38] PETERS A, DURNER W. Simplified evaporation method for determining soil hydraulic properties[J]. Journal of Hydrology, 2008, 356(1): 147－162.

[39] 薛绪掌, 张仁铎, 桂胜祥. 用薄层土蒸发数据计算获得萎蔫含水量和高基模吸力段持水曲线[J]. 土壤通报,2002, 33(2): 100－104.XUE Xu-zhang, ZHANG Ren-duo, GUI Sheng-xiang.Application of the evaporation process from thin soil samples[J]. Chinese Journal of Soil Science, 2002, 33(2):100－104.

[40] BITTELLI M, VENTURA F, CAMPBELL G S, et al.Coupling of heat, water vapor, and liquid water fluxes to compute evaporation in bare soils[J]. Journal of Hydrology, 2008, 362(3－4): 191－205.

[41] 徐斅祖, 王家澄, 张立新. 冻土物理学[M]. 北京: 科学出版社, 2001.

[42] 章金钊, 孙斌祥, 刘琦, 等. 透壁通风管路堤土体蒸发降温的试验研究[J]. 岩土力学, 2011, 32(6): 1813－1818.ZHANG Jin-zhao, SUN Bin-xiang, LIU Qi, et al.Laboratory investigation on water evaporative cooling effect in embankment with perforated ventilation pipe[J].Rock and Soil Mechanics, 2011, 32(6): 1813－1818.