基于不同溃口形态的尾矿坝溃决泥浆流动特性试验研究

敬小非，尹光志，魏作安，张千贵，王孟来

（1. 重庆大学 煤矿灾害动力学与控制国家重点实验室, 重庆 400030；2. 重庆科技学院 安全工程学院, 重庆 401331）

1 引 言

随着经济的蓬勃发展，我国对矿产资源的需求激增，当今已成为一个矿业大国，12种大宗矿产每年尾矿排放量约3亿吨，除小部分作为矿山充填或综合利用外，有相当部分尾矿采用构筑尾矿库的方式储存。据统计我国有尾矿库约6000余座，其尾矿坝安全形势不容乐观，尤其是近些年，尾矿坝的事故情况时有发生，造成了人员伤亡和巨大的经济损失，且给环境造成了毁灭性的破坏[1－4]。我国1/3的尾矿库属病险库，此类尾矿库因溃坝而导致灾难性事故不胜枚举[5－12]。加之尾矿坝溃坝具有突发性、一次灾情严重等特点，因而近年来成为防灾减灾的热点问题之一。由于不同溃口形态的尾矿坝溃坝泥浆在下游所表现出的流动特性具有较大差异性，因此，从尾矿坝溃口形态方面来研究尾矿坝溃坝泥浆流动特性，探索不同溃口形态下的溃坝泥浆对下游的灾害影响程度和范围，对矿山企业的防灾减灾工作具有重要的指导意义，同时为防灾预报和决策提供科学依据。

一般情况下，发生瞬间全部溃决的坝体多为刚性坝体，但刚性坝除了拱坝和峡谷的坝以外，实际上仍为局部溃坝，因此，坝体发生瞬间全部溃坝的可能性很小，而尾矿坝作为世界上特殊的人工堆积坝，其溃决形式也主要以局部溃坝为主。据资料显示[13]，除去拱坝外，不算战争因素引起的，溃坝口门比约在0.07～0.89之间，一般为0.5左右。因此，研究尾矿坝不同形式的局部溃坝具有重要的实际意义。

戴荣尧[14]、谢任之[15]、王国安[16]等分别对水坝不同溃口形态的坝址峰顶流量进行了探索性研究，并得出了水坝在不同溃决方式情况下的坝址峰顶流量公式。近期，韩中庚等[17]针对唐家山堰塞湖的具体问题，通过计算机仿真直观地显示了溃口变化、冲刷变化、溃口流量等过程，同时计算出1/3 溃坝时下游各地的洪水流量和洪峰到达时间。周建中等[18]又针对河道溃坝为水利工程防灾减灾中的突出问题，研究了平面河道溃口率分别为 0.1、0.2、0.4、0.6、0.8时流体在溃口处及下游的流场速度、压强等分布特性。研究成果对现场工程具有重要的指导意义。

然而，由于水坝与尾矿坝堆坝工艺各异，坝坡形状、坝体材料和功能以及运营过程中的浸润线位置差异较大，因此，水坝与尾矿坝在使用过程中的破坏机制和破坏形式也有所不同。水坝溃坝后，主要形成流量较大的洪水，而尾矿坝溃决后则形成危害程度更大的泥砂流。目前有关坝体瞬间局部溃坝的研究多集中于水坝溃坝，关于尾矿坝不同溃口形态的下泄泥浆流动特性研究至今鲜有报道。基于这一思路，本文以秧田箐尾矿库设计资料为依托，通过室内物理相似模型试验对不同溃口形态下的下泄泥浆流动特性进行研究。

2 尾矿坝溃决相似模拟试验

2.1 工程概况

秧田箐尾矿库为一座在建山谷型尾矿库，初步规划尾矿库最终有效库容为1.089 亿m3，属于二等库，堆坝方式采用上游式，在距尾矿库坝址下游600 m处有一90°弯道冲沟，米茂村在弯道外坡正对尾矿坝方向，整个地形如图1所示。

图1 尾矿库现场地形图Fig.1 Topographical map of tailings impoundment

2.2 试验目的

通过改变尾矿坝溃决口门大小，拟达到探索不同溃口形态下的尾矿坝溃决泥浆在下游沟谷中的流动特性，寻求溃口形态对泥浆流动的影响规律，更深入地认识尾矿坝溃决泥浆的运动特征。

2.3 试验装置

试验设备采用重庆大学自主研发的尾矿库溃决破坏相似模拟试验台（如图2所示），该试验台的主要功能是模拟尾矿坝溃决泥浆在下游冲沟中的传播特性，重点从宏观及定性的角度来研究下泄泥浆在演进过程中的流态特征、淹没高程、急弯处的反射特性以及冲击力变化规律，为深入了解尾矿坝溃坝泥浆的动力学特性提供了基础，并为下游防灾减灾工作的实施提供科学依据。本次试验主要是通过打开不同的闸门部位，以实现不同溃口形式的溃决。

2.4 试验内容

本次试验主要通过改变尾矿坝溃口大小（1/4溃坝、1/2溃坝、全溃）来研究不同情况下下泄泥浆流动特性。表1列出了本次模型试验的全部内容，每种情况重复进行3次试验，以实现数据统计采样的作用。泥浆浓度的选择主要参考了一般泥石流的浓度，并结合库区尾矿浆排放浓度最后确定。试验的原型材料为玉溪矿业易门矿务局铜厂铜矿现场排出尾矿砂（物理力学性质见表 2）。模型严格按照1∶400相似比尺制作。根据物理模型试验的相似原理[13,19－20]，相似材料选用黏性和粒径级配与原型矿浆相似的石膏粉浆体（其粒径分布规律见图 3）泥浆流态采用日本先进SONY数码摄像机进行全自动记录，该摄像机具有记录速度快（30帧/s）、数据记录和保存自动化等特点。

3 试验结果及分析

3.1 溃坝泥浆流态特性分析

根据测试结果，图 4、5分别给出了尾矿坝在1/4溃坝、1/2溃坝和瞬间全溃情况下各特征过流断面处的泥深变化规律。图6展示了尾矿坝在不同溃口形态下，泥浆到达急弯处后15 s时的流态特征。

图4 距坝址5 m处泥深变化过程曲线Fig.4 The slurry wave at 5 m of downstream

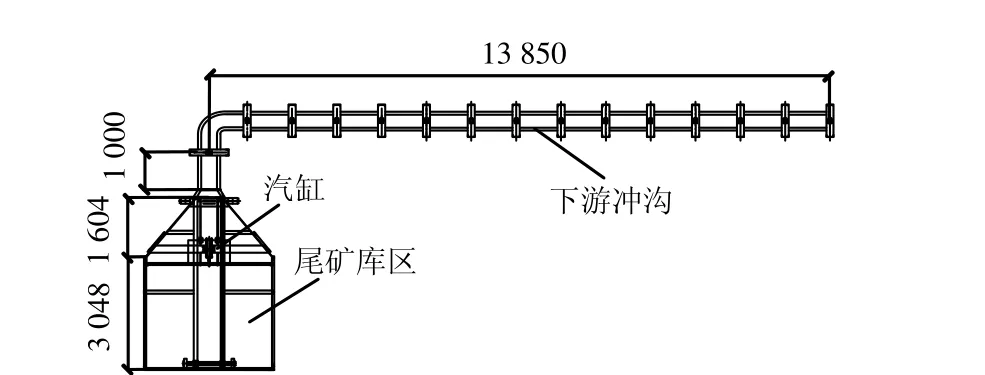
图2 尾矿库溃决试验台（单位：mm）Fig.2 Experimental tailings dam-break wave flume(unit: mm)

图5 距坝址7.5 m处泥深变化过程曲线Fig.5 The slurry wave at 7.5 m of downstream

表1 尾矿坝溃坝泥浆试验内容Table 1 List of dam-break wave experiments carried out in the laboratory flume

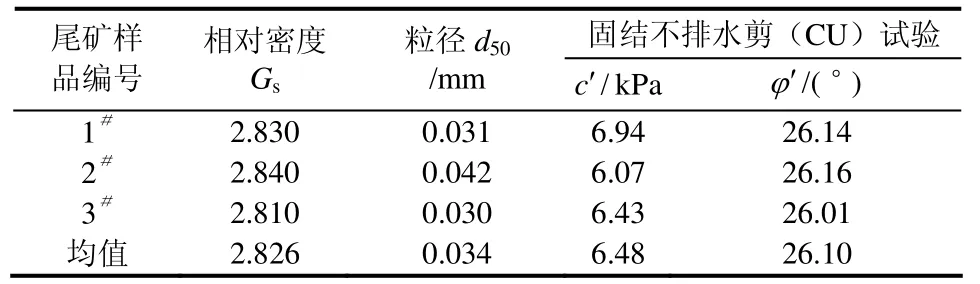
表2 原型尾矿砂物理力学性质Table 2 Physico-mechanical characters of prototype tailings

图3 试验用砂与原型砂颗粒粒径分布曲线Fig.3 curve of particle-size distributions of experiment and prototype

由图4、5（泥浆在5 m和7.5 m处泥深过程曲线）可得到以下规律：

（1）泥浆在到达各特征过流断面后出现较大幅度的波动现象，且不同溃决方式所表现出的波动幅度有所差异。瞬间全部溃决情况下，泥深波动幅值最大，而1/4溃决时，泥深的波动幅值最小，1/2溃决情况下泥深的波动幅度介于两者之间。分析其原因主要是由于泥浆在向下游传播过程中，途径下游1.5 m处的90°急弯时，泥浆出现不同程度的反射波，造成泥浆在向下游沟槽中的流动出现较大的波动现象，并将该震荡波不断地向下游传播。由于尾矿坝瞬间全部溃坝时，泥浆所具有的能量较大，泥浆到达急弯处时的流速较快，因而泥浆被急弯外坡所反射回来的能量也就较大，从而造成泥浆下游沟谷中的波动现象也就越明显，震荡幅度也就相应越大。随着泥浆不断地向下游演进，震荡波也向下传播，于是泥浆在急弯下游区域的传播过程同时伴随了泥深的震荡（见图 4、5）。由于急弯处造成了泥浆能量的损失和耗散，并随着后续泥浆向下游的不断传播及能量的衰减，泥浆在急弯下游各特征过流断面处的淹没高度波动幅度也逐渐弱化，最后泥浆在沟槽中平稳流动。随着溃坝口门的减小，泥浆所具有的能量不同程度的减弱，泥浆的波动现象相应被弱化，震荡幅值也相应衰减。1/4溃坝时，泥浆的震荡幅值最小，震荡所持续时间也最短，溃坝后泥浆很快进入了平稳流动过程。

（2）泥浆在下游各特征过流断面处的传播过程具有较明显的龙头衰减特性，泥深呈现小-大-小的分布，且具有较长的拖尾衰减现象。整个泥深过程曲线总体上可分为3个阶段。第1阶段：泥深迅速增长阶段。在该阶段内，泥浆龙头段到达该过流断面后的较短时间泥深迅速升高并达到峰值，在泥深变化过程曲线中反映的特性即此阶段曲线的斜率较大，曲线较陡。然而最大泥深是灾难性的，故该阶段也是整个过流阶段中最危险的阶段。泥深峰值到达的时间越短，表明撤离的时间越少，撤离越紧急，从而造成的灾害损失也就越大。第2阶段：泥深相对稳定阶段。该阶段内泥深基本稳定在峰值段，变化相对较缓慢，反映在曲线上即该段曲线斜率较小，曲线较平缓。第3阶段：泥深衰减阶段。在该阶段内，泥浆淹没高度呈缓慢减小特性，泥深从峰值逐渐降低直至泥浆停滞于沟谷中，泥浆淹没高度减小的速率较泥深上升速率小得多，该阶段最重要的特征为泥深降低速率小，持续时间长，约为前两个阶段持续时间总和的3倍。

不同的溃口形态所表现出的各特征过流断面处泥深过程曲线的形态也不尽相同，且每种溃口形态在下游同一过流断面处的泥深过程曲线所表现出的每个阶段持续时间也有较大差异。尾矿坝瞬间全部溃决情况下，泥浆淹没高度到达峰值的时间（即第1阶段）仅为2.7 s，而1/4溃坝情况下，泥深到达峰值的时间约为7.3 s，约为瞬间全溃的2.7倍。1/4溃坝时的泥深相对稳定阶段所持续时间大约为17 s，约占过流总时间的1/2，而瞬间全溃情况下第2阶段仅持续了5 s左右，并很快进入了第3阶段（泥深降低阶段）。瞬间全溃情况下泥深在第3阶段持续的时间较长，约占整个泥浆过流时间的 75%。1/4溃坝情况下，第3阶段的持续时间较瞬间全溃情况下要短，仅为10 s左右。

（3）对比分析5 m和7.5 m两处泥深过程曲线可知，二者最大差别表现在以下两点：

①7.5 m处第2阶段（泥深稳定阶段）所持续的时间较5 m处要长，7.5 m处的泥深稳定阶段基本上为泥浆到达此处后第3～20 s，所持续的时间达到了17 s，达到了整个过流时间的一半左右，约为5 m处的泥深稳定阶段持续时间的两倍。但7.5 m处所示的第3阶段（泥深缓慢降低阶段）持续时间仅为19 s，较5 m处相应的泥深缓慢降低阶段持续时间26 s短，仅为该处断面过流总时间的50%左右。距坝址7.5 m处，泥深过程曲线整体上较5 m处要平缓，泥深变化速率整体较小，说明距坝址越远，泥深过程曲线越平缓。

②7.5 m处的泥浆淹没峰值高度为7.8 cm，较5 m处的泥浆淹没峰值高度10.6 cm要小得多，说明距离坝址越远，泥浆淹没的最大高度也就越小，对该区域所造成的危害程度和影响范围也就越小。

由图6可知，溃决泥浆在90°急弯处流态变化强烈，在急弯内侧出现涡流现象，而在急弯外侧则出现泥浆反射现象，并出现明显的侧向爬升，泥浆在急弯两岸的泥深相差较大。瞬间全部溃坝条件下，溃后泥浆到达急弯后15 s时形成涡流和反射波较相同条件下的1/2和1/4溃决情况下要明显，且涡流出现的范围也明显比其他两种溃决形式要大得多。随着尾矿坝溃口的加大，泥浆在急弯处的侧向爬升高度呈增大趋势。这种现象可解释为，由于泥浆到达急弯处时，靠近沟谷凹岸一侧，受到离心力的作用，流动速度几乎减小到 0，这样动能v2/2g转化为位能，造成泥浆沿沟谷外坡爬高，引起局部泥浆淹没高度升高，加重了溃坝的灾害程度。而且随着尾矿坝溃口的加大，泥浆初始能量增大，下游转弯处的侧向淹没高度将进一步升高。

图6 溃后泥浆到达急弯后15 s时形成涡流和反射波Fig.6 The vortex and reflection waves after slurry arrived at sharp bend flume 15 s

3.2 溃坝泥浆波峰传播规律分析

在试验过程中采用 SONY数码摄像机对溃坝泥浆波峰到达下游各特征过流断面时的瞬态进行捕获，获得了不同溃口形态下，下游不同特征过流断面处的泥浆龙头段波峰自由面图，如图 7～9所示。

从图7～9可以看出，尾矿坝溃坝以后，泥浆以一个很陡峭的波峰形式向下游传播，波峰的高度在最初一瞬时达到坝高的40%～60%，但随着泥浆向下游不断传播而有所减小。这种现象主要归因于下游沟槽阻力和泥浆自身黏聚力的影响，急弯对泥浆能量也造成了很大损耗，尽管同时底坡在起反作用。在距坝址较远处，波峰基本完全平坦化，而成为渐变流。

在波峰到来时，泥深瞬时突然增大，波峰过后，泥深增长平缓，基本稳定在峰值段附近，泥深在某时刻达到极值，而后逐渐减小。随着尾矿坝溃口的变化，下游各特征过流断面处的波峰高度变化较大，对比图7(a)和图9(a)可以发现，随着溃口不断减小，同一过流断面处的波峰高度衰减速度较快，瞬间全溃情况下坝址处波峰高度几乎为1/4溃决情况下的3倍左右。

图7 瞬间全部溃坝泥浆到达下游各特征过流断面处时的波峰自由面图Fig.7 The flow pattern of wave peak in some characteristic sections of the experimental channel in the entire instantaneous collapse conditions

图8 1/2溃坝泥浆到达下游各特征过流断面处时的波峰自由面图Fig.8 The flow pattern of wave peak in some characteristic sections of the experimental channel in the 1/2 instantaneous collapse condition

图9 1/4溃坝泥浆到达下游各特征过流断面处时的波峰自由面图Fig.9 The flow pattern of wave peak in some characteristic sections of experimental channel in 1/4 instantaneous collapse condition

3.3 溃坝泥浆流速特性分析

根据试验过程中数码摄像机的记录结果，分析获得了不同溃口形态情况下，尾矿库溃决泥浆在各特征过流断面处的速度过程特性曲线（见图 10、11）。试验中，采用跟踪式速度测量方法，采用直径为φ10 mm的白色泡沫小球进行流速跟踪计算，根据小球冲击的时间及运动路程计算泥浆流动速度，试验进行3次，以实现数据统计采样的作用。

图10 尾矿坝溃坝泥浆在5 m处的流速过程线Fig.10 The slurry velocities at 5 m of downstream

由图10、11可分析得出，尾矿坝溃坝后，泥浆以一个较大速度向下游传播，随着泥浆向下游不断演进而逐渐减小。同时伴随着尾矿坝溃口不断减小，泥浆到达下游同一过流断面处时的流动速度也相应减小，且不同特征过流断面处泥浆流动速度减小幅度有所不同。在5 m处，瞬间全溃情况下泥浆流速较1/4溃决时减小50%左右，而在7.5 m处，瞬间全溃情况下泥浆流速较1/4溃决时减小约42%，表明不同溃口形态下，泥浆在5 m处的流速减小梯度要大于在7.5 m处的流速减小梯度，同时说明了随着泥浆向下游不断地推进，溃坝口门形态对泥浆流速的影响程度在不断被弱化。

泥浆在距坝址下游5 m和7.5 m处的流速变化特性可分为3个阶段。

（1）流速加速降低阶段（龙头段）。该阶段主要集中在溃坝泥浆到达各特征断面处初期，溃坝泥浆龙头段到达下游各过流断面处时，龙头速度较快，但随即迅速减小，持续时间在10～15 s左右，且不同断面处，该阶段的持续时间有所差异。瞬间全溃情况下，泥浆在5 m处，龙头段流速减小所持续的时间在10.6 s左右，而在7.5 m处，龙头段流速减小所持续的时间约为15.4 s，是5 m处的1.5倍左右。而在不同溃口形态下，同一过流断面处第1阶段所持续时间也有所不同。在5 m处，瞬间全溃情况下龙头段流速减小所持续的时间在10.6 s左右，在1/2溃决情况下，龙头段流速减小所持续的时间在8.2 s左右，而在1/4溃决情况下的持续时间仅为4.2 s。

（2）流速稳定阶段（龙身段）。该阶段主要为泥身过流阶段，此阶段泥浆来流相对较平稳，泥浆流速也保持在一个相对较稳定的阶段，只是在不同溃口形式下，泥浆在该阶段所持续的时间有所不同。

（3）流速稳定降低阶段（龙尾段）。由于上游泥浆来流量逐渐减小，且龙尾段泥浆所具有的能量也逐渐降低，故该阶段内泥浆流动速度呈稳定减小趋势，直至泥浆停滞。

3.4 溃坝泥浆冲击力测试结果

图12展示了不同溃口情况下尾矿库溃决泥浆在下游1 m处的冲击力变化规律。由图可知，溃口形式对泥浆冲击力有较大影响，随着尾矿坝溃坝口门的减小，泥浆冲击力以及冲击力峰值到达时间均呈减弱趋势。冲击力时程曲线前端较陡，后端相对平滑，冲击力峰值出现在泥浆龙头段，随后迅速减小。这表明泥浆龙头段较后续泥浆的冲击力要大，且冲击过程是在较短时间内完成的。冲击力峰值和最大泥深决定了溃坝泥浆对下游的灾害程度，冲击力峰值和最大泥深越大，下游的灾害程度越严重。

4 讨 论

近几年来，国内外发生尾矿坝溃决事故不甚枚举，不仅对矿山企业和下游造成了巨大生命和财产损失，而且对周边环境造成了毁灭性的破坏。除此之外，尾矿库溃坝造成的交通中断，电力系统的破坏等后果也是非常严重的。这一系列问题引起了业内外相关学者的高度重视。由于不同的尾矿坝溃决，所形成的溃决口门形式往往不尽相同，其下泄泥浆所表现出的流动特性差别较大。因此，探索不同溃口条件下的尾矿坝溃决泥浆流动特性具有重要的现实意义，同时为矿山企业的防灾减灾工作提供了科学依据。

由于溃坝泥浆具有流量大、破坏性强以及突发性等特征，通常难以对现场尾矿坝溃坝资料进行实测，而相关的尾矿坝溃决泥浆运动学理论尚未形成相关体系，因此，溃坝模型试验是当前研究尾矿坝溃决泥浆流动特性的主要手段。尾矿坝溃坝模型试验可研究溃坝泥浆在下游的运动机制，并验证理论计算（数学模型）成果，在复杂三维地形中给出较直观的概念，这些都是其优点所在。但也存在投资大、费时高、制作难的一些不足之处。本次试验在参考了业内诸多专家的研究成果基础之上，从尾矿坝溃口形态角度出发，探索了溃口形态对尾矿坝溃坝泥浆流动特性的影响特征，获得了一些有益的成果。

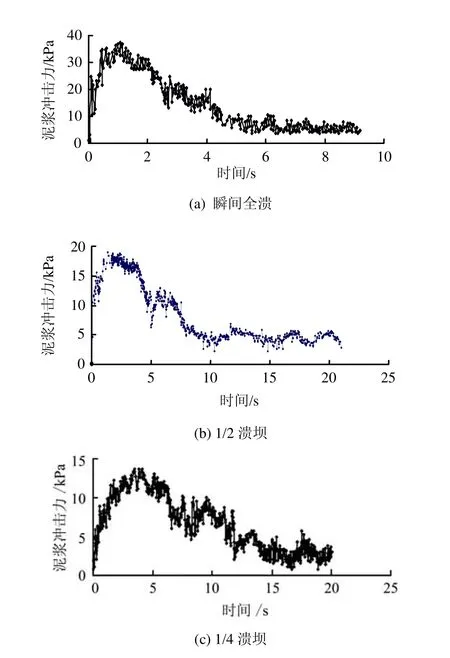
图12 不同溃口形式情况下距坝址1.0 m处泥浆冲击力过程曲线Fig.12 The impact stress at 1.0m of downstream in the three kinds of collapse gates

但在此次试验中也存在一些问题。由于糙率的大小对泥浆在下游的传播特性关系较大，但尾矿库库区下游沟谷的糙率资料却比较少，因此，模型糙率的选用和率定就成为了一大难题。本次试验以不同溃口形态下的最大破坏形式为目的，故下游沟槽采用光滑透明的有机玻璃，未考虑糙率对泥浆流动特性的影响，但课题组将就糙率对溃坝泥浆流动特性的影响关系问题作进一步的深入研究。同时，尾矿坝现场下游沟谷地形往往比较复杂，而此次试验对下游沟槽进行了简化，仅研究了规则沟槽情况下的溃坝泥浆流动特性，但沟谷宽度变化对溃决泥浆的传播特性有明显地影响，因此，开展在不同宽度（沟槽断面收缩或扩大）的沟槽中研究溃坝泥浆运动特性具有很强的现实意义。

此外，目前有关尾矿坝溃决泥浆的流速、流量、泥深以及冲击力计算公式还借用泥石流计算公式，由于尾矿坝溃坝具有水坝溃坝和泥石流流动的双重特性，它既不同于水坝溃坝，也与泥石流也具有本质区别，因此，研究冲击力、流速以及泥深之间的相互关系，并推导出一套适合尾矿坝溃坝泥浆流动特征参数的计算公式是今后的主要研究方向。

5 结 论

（1）尾矿坝溃决泥浆到达各特征过流断面后出现较大幅度的波动现象，瞬间全溃情况下泥浆流态的波动幅度最大，1/4溃口形态下泥浆流态波动幅度最小。随着泥浆不断地向下游传播，波动现象逐渐减弱。泥浆在特征过流断面处的泥深过程曲线整体上可分为3个阶段：①泥深迅速增长阶段；②泥深相对稳定阶段；③泥深降低阶段。不同的溃口形态所表现出的各过流断面处泥深过程曲线特征却不尽相同，每种溃口形式在同一过流断面处的过流过程中3个阶段的持续时间有较大差异。

（2）溃决泥浆在下游90°弯道处变化强烈，在急弯的内侧出现涡流现象，而在急弯的外侧则出现泥浆反射现象，急弯两侧的泥深差异较大。瞬间全部溃坝较1/2和1/4溃口形态下要明显。随着尾矿坝溃口的加大，泥浆在急弯处的侧向爬升高度呈增大趋势。尾矿坝溃坝后，泥浆以一个很陡峭的波峰形式向下游传播，随着泥浆向下游的不断传播而有所减小。在距坝址较远的情况里，波峰基本完全平坦化，而成为渐变流。随着溃口的不断减小，同一过流断面处的波峰高度衰减速度较快，瞬间全溃情况下坝址处波峰高度为1/4溃决情况下的3倍左右。

（3）随着尾矿坝溃口不断减小，泥浆到达下游同一过流断面处时的流动速度相应减小，且减小幅度有所不同。各溃口形态下的溃决泥浆在下游同一过流断面处的流速减小梯度也有所差异，泥浆在5 m处的流速减小梯度要大于在7.5 m处的流速减小梯度，泥浆距坝址越远，溃口形式对泥浆流速的影响幅度也就越小。

（4）随着尾矿坝坝体溃口的减小，同一过流断面泥浆最大冲击力呈减弱趋势，冲击力峰值到达时间也呈减小趋势。冲击力时程曲线前端较陡，后端相对较平滑，冲击力峰值出现在泥浆龙头段。

[1] 魏作安, 尹光志, 沈楼燕, 等. 探讨尾矿库设计领域中存在的问题[J]. 有色金属(矿山部分), 2002, 54(4): 44－48.

[2] KWAK M, JAME D F, KLEIN K A. Flow behavior of tailings paste for surface disposal[J]. International Journal of Mineral Processing, 2005, 77(3): 139－153.

[3] CABRERA F, ARIZA J, MADEJÓN P, et al. Mercury and other trace elements in soils affected by the mine tailing spill in Aznalcóllar (SW Spain)[J]. Science of the Total Environment, 2008, 390(2－3): 311－322.

[4] MILTON A, COOKE J A, JOHNSON M S. A comparison of cadmium in ecosystems on metalliferous mine tailings in Wales and Ireland[J]. Water, Air, & Soil Pollution,2004, 153(1－4): 157－172.

[5] HUDSON-EDWARDS K A, MARKLIN M G,JAMIESON H E, et al. The impact of tailings dam spills and clean-up operations on sediment and water quality in river systems: The Ríos Agrio-Guadiamar, Aznalcóllar,Spain[J]. Applied Geochemistry, 2003, 18(2): 221－239.

[6] GRIMALT J O, FERRER M, MACPHERSON E. The mine tailing accident in Aznalcollar[J]. Science of the Total Environment, 1999, 242(1－3): 3－11.

[7] RICO M, BENITO G, SALGUEIRO A R, et al. Reported tailings dam failures: A review of the European incidents in the worldwide context[J]. Journal of Hazardous Materials, 2008, 152(2): 846－852.

[8] HARDER L F J, STEWART J P. Failure of Tapo Canyon tailings dam[J]. Journal of Performance of Constructed Facilities, 1996,10(3):109－114.

[9] RICO M, BENITO G, DÍEZ-HERRERO A. Floods from tailings dam failures[J]. Journal of Hazardous Materials, 2008, 154(1－3): 79－87.

[10] 徐宏达. 我国尾矿库病害事故统计分析[J]. 工业建筑,2001, 1(31): 69－71.

[11] ÁLVAREZ-VALERO A M, SÁEZ R. Evaluation of heavy metal bio-availability from Almagrera pyrite-rich tailings dam (Iberian Pyrite Belt, SW Spain) based on a sequential extraction procedure [J]. Journal of Geochemical Exploration, 2009, 102(2): 87－94.

[12] 魏勇, 许开立, 郑欣. 浅析国内外尾矿坝事故及原因[J].金属矿山, 2009, 397(7): 139－142.WEI Yong, XU Kai-li, ZHENG Xin. Discussion on the causes for tailings dam accidents at home and abroad[J].Metal Mine, 2009, 397(7): 139－142.

[13] CHENG Zun-lan, DANG Chao, LIU Jing-jing, et al.Experiments of debris flow damming in Southeast Tibet[J]. Earth Science Frontiers, 2007, 14(6): 181－185.

[14] 戴荣尧, 王群. 溃坝最大流量的研究[J]. 水利学报.1983, (2): 13－21.DAI Rong-yao, WANG Qun. Research on the maximum discharge of dam-breaking[J]. Journal of Hydraulic Engineering, 1983, (2): 13－21.

[15] 谢任之. 溃坝水力学[M]. 山东: 山东科学技术出版社,1989: 74－75.

[16] 王国安. 坝体瞬间全溃最大流量通用公式推导[J]. 华北水利水电学院学报, 2001, 22(3): 23－30.WANG Guo-an. Derivation of maximum flow general formula about instantaneous total dam-break[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power, 2001, 22(3): 23－30.

[17] 亢宁, 李鹏, 杨森. 唐家山堰塞湖泄洪问题研究[J]. 数学的实践与认识, 2009, 39(16): 27－36.KANG Ning, LI Peng, YANG Sen. Research on sluicing of Tangjiashan Quake Lake[J]. Mathematics in Practice and Theory, 2009, 39(16): 27－36.

[18] 黄志伟, 周建中, 郭双喜, 等. 平面河道溃口绕流分析及流体对溃坝冲击的影响[J]. 水电能源科学, 2010,28(1): 83－85.HUANG Zhi-wei, ZHOU Jian-zhong, GUO Shuang-xi,et al. Analysis of flow around dam breach and fluid impact on dam break[J]. Water Resources and Power,2010, 28(1): 83－85.

[19] 杨俊杰. 相似理论与结构模型实验[M]. 武汉: 武汉理工大学出版社, 2005.

[20] 王协康, 方铎. 泥石流模型试验相似律分析[J]. 四川大学学报(工程科学版), 2000, 32(3): 9－12.WANG Xie-kang, FANG Duo. Study of laws of debris model similarity[J]. Journal of Sichuan University(Engineering Science Edition), 2000, 32(3): 9－12.