单臂集束型装备随机Petri网模型与性能分析

郑秀红， 胡静涛

(1.沈阳化工大学计算机科学与技术学院，辽宁沈阳 110142;2.中国科学院沈阳自动化研究所信息服务与智能控制研究室，辽宁沈阳 110016)

集束型装备(Cluster tools)是当今半导体制造中使用的一类主要装备，根据SEMI标准E21-96，集束型装备是一种集成的、包含机械连接在一起的多个处理模块，传输模块和晶圆承载室的半导体制造设备.随着半导体加工过程中集成度的提高，集束型装备的配置变得越来越复杂，装备的吞吐量，晶圆的生产周期和加工腔体利用率等特性不仅与晶圆处理时间有关，还与集束型装备的一些其他属性有关，如晶圆承载室参数，机械手参数，腔体参数和晶圆处理流程参数等都对装备产能、加工周期有影响.在装备配置的不确定性和复杂的晶圆处理流程的双重影响下，对产能的预测更加困难.建立集束型装备的加工过程模型在预测集束型装备性能和优化系统配置上成为非常必要的解决方式.

仿真是一种预测装备性能的方法，LeBaron采用商业仿真软件AutoMod开发了一个灵活、高精度的集束型装备仿真模型，模拟装备运行［1-2］.IBM的工程师Shikalgar等用6年多的时间研究了一个仿真模型来模拟半导体300 mm生产线的实际加工过程，应用该仿真模型可以得到更加准确的产能结果［3］.Gupta开发了一个仿真模型，验证并分析了单臂机械手集束型装备的最大吞吐量理论模型［4］.但实践证明，仿真是一种非常费时费力的方法.Petri网是Petri博士在1962年提出的一种系统描述和分析工具，它处理动态离散事件和复杂系统时具有图形表示和数学描述双重功能，因此成为半导体制造中集束型装备生产线强有力的工具，可用于设备的建模和分析.Srinivasan首先建立了Petri网模型，分析了集束型装备的性能［5］.考虑加工过程的持续时间因素，Zuberek利用赋时Petri网为集束型装备建模，模型涉及到很多类集束型装备，如单臂机械手，双臂机械手、多机械手，可重入等装备，最后利用结构化分析方法分析模型，计算装备性能［6-7］.白丽平和伍乃琪用面向资源的着色赋时Petri网构造了集束型装备的模型，分析了装备的性能［8-9］.对于集束型装备的调度问题也有了一些研究，伍乃骐构造了系统的Petri网模型并确定了实时控制策略，对双臂集束型装备的晶圆驻留时间变化作了详细的分析，推导出了一个有效方法.应用该方法可以进行系统可调度性分析，以找到优化的调度方案［10］.

目前，大部分研究都是针对应用赋时Petri网对集束型装备建模，即所有变迁的时间是确定的、不变的，但是，该模型不能准确地反映装备运转的实际情况，因为实际运转过程中装备的处理时间并不是一个固定值，而是符合一定概率分布的随机值.所以，针对这一问题本文提出利用随机Petri网对集束型装备建模，然后，构造同构的马尔可夫过程，分析马尔可夫过程，计算装备的吞吐量和处理模块的利用率.

1 集束型装备

1.1 装备结构

集束型装备的结构如图1所示.通常集束型装备由处理模块(process module，PM)，晶圆承载室(Loadlock，LL)和一个基于机械手的传输模块(Transfer Module)组成.处理模块负责加工晶圆，大多处理模块都是单晶圆的，即同一时间只能处理1个晶圆.机械手有单臂机械手和双臂机械手2种，它负责为处理模块卸载、加载和移动晶圆，单臂机械手1次只能处理1片晶圆，如图1所示.而双臂机械手可同时承载2片晶圆.晶圆承载室负责待处理和处理后晶圆的存放.

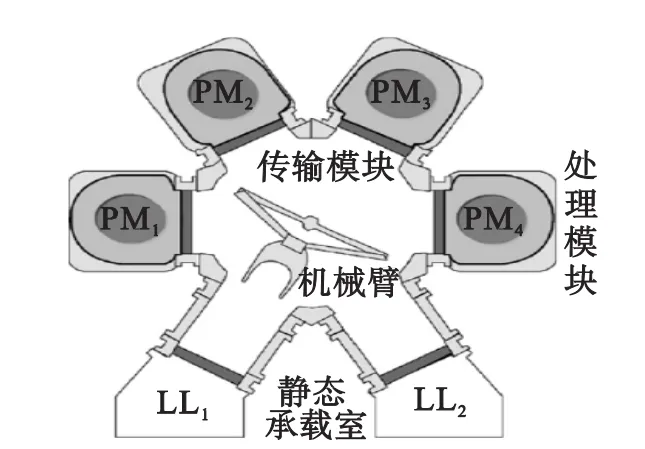
图1 集束型装备Fig.1 Cluster tools

1.2 晶圆的加工流程

晶圆的处理模式可根据配方灵活调整，因此，一个集束型装备可以处理很多种晶圆流模式.通常根据晶圆流模式的不同，可把集束型装备分为并行集束型装备和串行集束型装备.并行集束型装备含有1个以上的处理模块执行相同的晶圆加工操作步骤.而在串行集束型装备中，各个处理模块执行不同的加工操作，晶圆必须遍历所有处理模块才能够完成加工处理.

以图1为例，假设处理模式为串行，单臂机械手，装备开始时处于闲置状态，晶圆的处理顺序为 LL1→PM1→PM2→PM3→PM4→LL2.有一批晶圆(通常包含25片晶圆)要加载到集束型装备的晶圆承载室LL1中，系统的加工过程如图2所示.

图2 晶圆的加工流程Fig.2 The process procedure of wafer

图2中箭头表示机械手从一个腔体向另一个腔体移动晶圆.Wi表示第i片晶圆.

一批晶圆从进入集束型装备到离开装备要依次经过加载，初始暂态，稳态，结束暂态，卸载5个系统状态.在5个状态中，稳态具有周期性特点，且系统处于稳态的时间最长，所以，对装备运转过程的建模分析，关键就是对稳态时装备运转流程进行建模，以分析装备的性能.

2 随机Petri网及分析方法

假设变迁Ti拥有一个时延di(di为从变迁从被授权到引发的时间延迟)，其中，di是一个非负的、连续的、服从指数分布的随机变量X，分布函数如下:

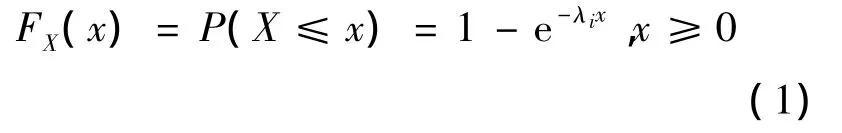
随机 Petri网(Stochastic Petri Net，SPN)是一类变迁拥有上述时延特性的Petri网［11］.一个随机 Petri网就是一个五元组(P，T，F，m0，Λ)，其中，Λ:T→R+是一个与所有变迁的引发速率相关的引发函数，通常用λi表示变迁Ti的引发速率，那么，变迁Ti的平均时延就为

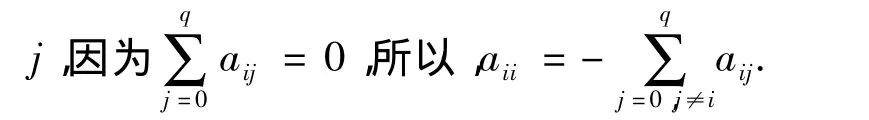
分析马尔可夫过程，稳态时状态的概率分布Π =(π0，π1，…，πq)满足:

其中，A=(aij)(q+1)×(q+1)是变迁率矩阵.通过稳态概率Π和引发函数Λ，可分析出系统性能.

3 建模

建立描述集束型装备加工过程的SPN模型的步骤如下:

步骤1 确定系统配置，如腔体数量，机械手类型，调度策略等;此处分析的集束型装备是一个2-腔体的单臂集束型装备.2个处理腔体执行不同的功能，机械手1次只能取运送1个晶圆，只有1个晶圆承载室LL.假设所有的晶圆都有相同的处理步骤，没有任何腔体可重入.处理流程串行的，LL→PM1→PM2→LL.

步骤2 分析集束型装备稳态的加工过程，如图2所示.

步骤3 根据稳态时期的装备加工过程，确定晶圆流路径，稳态时的晶圆序列:LL⇒PM1→PM2⇒LL→PM1⇒PM2→LL，其中符号“⇒”表示机械手带晶圆移动，符号“→”表示空机械手移动.

步骤4 确定装备运行时的主要操作，如加载、卸载晶圆、机械手移动、加工等操作，以及操作的输入库所集和输出库所集.如表1所示.

表1 主要变迁及其输入库所和输出库所集Table 1 The input place and output place of the main transition

步骤5 用表1作导向，构造随机Petri网模型，如图3所示.图3中变迁和库所的描述如表2和表3所示.λi表示变迁Ti的引发率.

图3 单臂集束型装备的SPN模型Fig.3 The SPN model of the single-blade robot cluster tools

表2 模型中变迁的描述Table 2 The transition description

表3 模型中库所的描述Table 3 The place description

步骤6 根据系统的稳态特性，稳态开始时，机械手为空，且处于LL处，处理腔体1为空，处理腔体2中有一片晶圆，P5，P3，P7都有一个托肯，所以模型的初态m0=(001010100000).

步骤7 验证模型.采用软件包Visual Object Net++［13］验证Petri网模型的行为属性，通过该软件包的验证，表明该模型是活的、有界的，可达的.因此，可采用马尔可夫方法分析模型.

4 模型分析

4.1 构造可达图

从系统初始状态m0出发，得到系统可到达的所有状态以及状态间的关系，构造可达图，m0可到达的状态有13个，所有状态的库所标识如表4所示.

表4 可达标识集列表Table 4 The reachability set

4.2 马尔可夫过程

在集束型装备的SPN模型中所有变迁都服从指数分布，变迁Ti服从参数λi的指数分布，根据模型可达图和变迁的特性得到同构的马尔可夫过程，如图4所示.

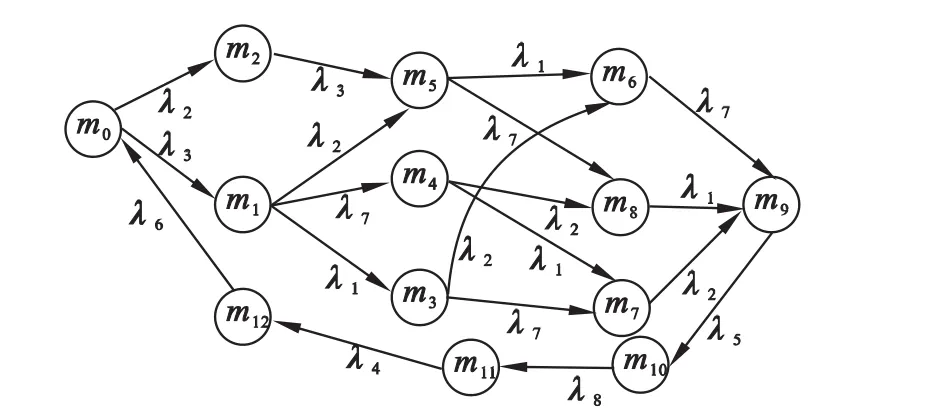
图4 同构的马尔可夫过程Fig.4 The equivalent Markov process

4.3 马尔可夫过程分析

取 λ1=λ2=0.1，λ3=λ4=λ5=λ6=λ7=λ8=1，所有状态的概率分布 Π =(π0，π1，…，π12)，满足方程组(3)，解得:

π =(0.046 46，0.038 72，0.004 65，0.003 52，0.193 57，0.007 74，0.001 13，0.228 8，0.271 01，0.051 1，0.051 1，0.051 1，0.051 1).

4.4 装备性能分析

4.4.1 系统吞吐量

系统的吞吐量，即单位时间加工的晶圆数量，它是评价集束型装备性能最重要的指标.由表2可知，变迁T5代表晶圆经过PM1，PM2处理完成，机械手将其取出放入LL中，同时根据图4可确定只有在状态m9时，T5可以被授权.那么系统的吞吐量根据如下方法［14］得到:

WHP=f5=λ5π9=1 ×0.051 1=0.051 1.因此，每个晶圆的处理时间约为:

T=1/WHP=1/0.051 1=19.57.

4.4.2 处理模块利用率

各个模块利用率的差值是改善装备配置，提高装备吞吐量的重要依据.由表3可知，状态P5代表PM1腔体为空，处于闲置状态;由表4可知，只有状态 m0，m2，m12的 P5中托肯数为 1，所以，PM1的利用率［14］为:

UPM1=1-(π0+π2+π12)=0.897 79.

即处理模块PM1的利用率为89.779%.同理，可计算PM2的利用率为89.78%.

5 结论

提出了集束型装备的随机Petri网模型，经验证，该模型是活的、有界的.推导有界模型的可达图，确定同构的马尔可夫过程，通过分析马尔可夫过程，计算装备的吞吐量和模块利用率.与赋时Petri网方法相比，该模型中变迁的时延是随机的，更符合装备实际运转情况，因此计算的性能更准确.但是对随机Petri网模型分析过程中需要构造模型的可达图，推导出模型的所有状态才能构造同构的马尔可夫过程，所以，该方法不适合大型系统的建模和分析.

［1］ LeBaron H T，Pool M.The Simulation of Cluster Tools:a New Semiconductor Manufacturing Technology［C］//Proceedings of the 1994 Winter Simulation Conference.USA:IEEE，1994:907-912.

［2］ LeBaron H T，Hendrickson R A.Using Emulation to Validate a Cluster Tool Simulation Model［C］//Joines J A，Barton R R，Kang K，et al.Proceedings of the 2000 Winter Simulation Conference.USA:IEEE，2000:1417-1422.

［3］ Shikalgar S T，Fronckowiak D，MacNair E A.Application of Cluster Tool Modeling to a 300 mm Fab Simulation［C］//Chick P J，Sánchez P J，Edward A，et al.Proceedings of the 2003 Winter Simulation Conference.USA:IEEE，2003:1394-1397.

［4］ Gupta A K，Lendermann P，Sivakumar A I，et al.Simulation Analysis of Cluster Tool Operations in Wafer Fabrication［C］//Proceedings of the 2008 Simulation Conference.USA:IEEE，2008:2141-2147.

［5］ Srinivasan R S.Modeling and Performance Analysis of Cluster Tools Using Petri Nets［J］.IEEE Transactions on Semiconductor Manufacturing，1998，11(3):394-403.

［6］ Zuberek W M.Timed Petri Nets in Modeling and A-nalysis of Cluster Tools［J］.IEEE Transactions on Robotics and Automation，2001，17(5):562-575.

［7］ Zuberek W M.Cluster Tools with Chamber Revisiting-modeling and Analysis Using Timed Petri Nets［J］.IEEE Transactions on Semiconductor Manufacturing，2004，17(3):333-344.

［8］ 白丽平，伍乃骐.半导体制造中具有非重入过程的自动组合装置的性能分析［J］.系统工程理论与实践，2005，6:11-18.

［9］ 白丽平，伍乃骐.半导体重入加工过程自动组合装置的建模与分析［J］.计算机集成制造系统，2005，11:320-325.

［10］ Wu N Q，Zhou M C，Analysis of Wafer Sojourn Time in Dual-arm Cluster Tools with Residency Time Constraint and Activity Time Variation［J］.IEEE Transactions on Semiconductor Manufacturing，2010，23(1):53-64.

［11］ Zhou M C，Jeng M D.Modeling，Analysis，Simulation，Scheduling，and Control ofSemiconductor Manufacturing Systems:a Petri Net Approach［J］.IEEE Transactions on Semiconductor Manufacturing，1998，11(3):333-357.

［12］ Mollog M K.Performance Analysis Using Stochastic Petri Nets［J］.IEEE Transactions on Computers，1982，31(9):913-917.

［13］ Drath R.Petri-Net-CAD/CAE-Tool:Visual Object Net++1.44［EB/OL］.(2008-07-10)［2011-12-10］.http://www.systemtechnik.tu-ilmenau.de/%7Edrath/visual_E.htm.

［14］江志斌.Petri网及其在制造系统建模与控制中的应用［M］.北京:机械工业出版社，2004:98-100.