卧式行星球磨机最佳参数的数值模拟

朱 飞，张林进，蔡道林，叶旭初

（南京工业大学 材料科学与工程学院 材料化学工程国家重点实验室，南京210009）

卧式行星球磨机最佳参数的数值模拟

朱 飞，张林进，蔡道林，叶旭初

（南京工业大学 材料科学与工程学院 材料化学工程国家重点实验室，南京210009）

卧式行星球磨机（以下简称卧式行星磨）是一种新型粉磨设备，它由若干个磨筒均匀安装在竖直放置公转圆盘上，磨筒自转的同时围绕圆盘中心进行公转，从而实现在离心力场中进行粉磨，超越了重力场的速度限制，公转和自转同时以较高速度运转使钢球获得巨大的撞击力，提高对物料的粉磨效率，达到节能效果［1－3］。

在行星磨应用最早的是Cundall和Strack在1979年利用离散元法（Distinct Element Method，DEM）模拟技术模拟无机材料在行星磨中的粉磨效率［4］，日本东北大学的Kano，Saito和 Mio等人对立式行星磨进行了DEM模拟研究［5－9］。作者已经对卧式行星磨进行过离散元模拟研究，模拟证明了钢球的抛落状态与钢球平均接触力的关系［10］。本工作采用离散元法模拟公转转速对磨筒内钢球平均接触力的影响，用卧式行星磨样机研究公转转速对粉磨速率的影响，以公转转速为媒介构建粉磨速率和平均接触力的关系，在此基础上，模拟分析卧式行星磨的填球率、钢球直径、磨筒半径和公转半径等因素对钢球平均接触力的影响规律。

1 实验

所用原料是密度为3.128g/cm3的水泥熟料，选择粒度为6～8目（2.36～3.35mm）用于粉磨实验，表1为其化学组成。实验所用卧式行星球磨机如图1所示，磨筒有效直径为89mm，深度为78mm，磨筒容积为485cm3，公转半径140mm。磨筒内周向均匀分布6根钢质衬板，宽度为7mm，厚度为3mm，与磨筒的连接方式为无螺栓连接即衬板镶嵌在磨筒内部，磨筒内的研磨体是密度为7.85g/cm3的钢球，直径φ12mm。实验内容是在某一固定公转转速下，粉磨时间分别为0.5，1，2，3，4min，根据公式（3）计算出这一转速下的粉磨速率，最后得出公转转速与粉磨速率的关系。

表1 水泥熟料的化学组成Table 1 Chemical composition of cement clinker

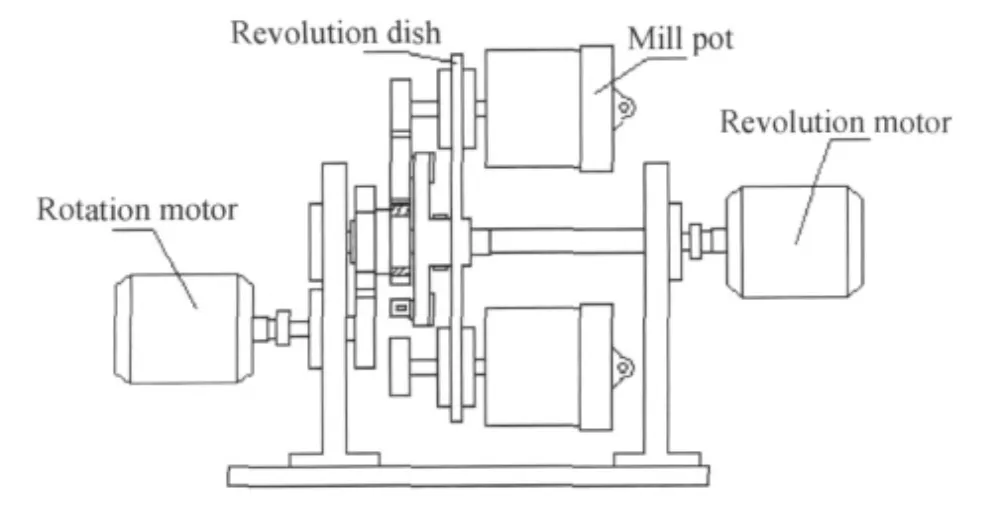
图1 多功能卧式行星球磨机结构图Fig.1 Schematic diagram of the multi－functional horizontal planetary ball mill

2 离散元模拟

离散元模拟以颗粒流模型PFC3D软件为分析平台，利用fish语言编写程序进行二次开发和数值试验方案设计。接触模型如图2所示，在任意时间步长内接触力的计算方程如式（1），（2）所示。

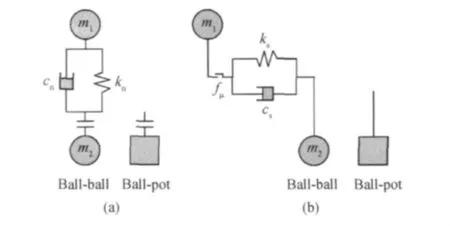
图2 接触模型 （a）法向力；（b）切向力Fig.2 Contact model （a）compressive force；（b）shear force

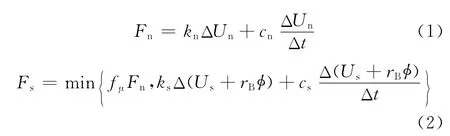
式中：k是弹性系数；c是阻尼系数；n和s表示法向和切向；U和φ分别是相对位移和相对角位移；fμ是滑动系数；rB是钢球半径。

具体的模型计算参数如表2所示。

表2 行星磨离散元模型计算参数Table 2 The parameters of planetary ball mill DEM model

3 实验结果与讨论

图3为不同公转转速粉磨水泥熟料的wi（t）/wi（0）与粉磨时间的关系，wi（t）和wi（0）分别是破碎t时间后和原始物料在2.36～3.35mm粒级物料的质量比率。图3（a）是填球率ηb（ηb＝Vb/Vm，Vb和Vm分别是钢球和磨筒的体积）为10%，物料体积V＝15.22cm3；图3（b）是ηb为15%，V＝22.78cm3，两组实验物料和钢球的体积比都是1∶3.2。对结果进行拟合可知2.36～3.35mm水泥熟料可以用一级粉磨动力学方程描述。

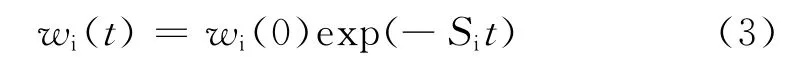
式中：wi（0），wi（t）表示破碎前和破碎t时间2.36～3.35mm粒级物料的质量比率；Si表示该粒级物料的破碎速率；t为破碎时间。

根据图3拟合的数据代入公式（3）计算出行星磨粉磨速率Si，作出不同磨筒填球率ηb条件下卧式行星磨粉磨速率Si与公转转速Nr之间的关系，如图4（a）所示，粉磨速率随着公转转速的增加而变大，随着转速增加粉磨速率增加幅度变大，以ηb为10%为例，公转转速为100r/min和300r/min的粉磨速率Si为0.072，0.872min－1。

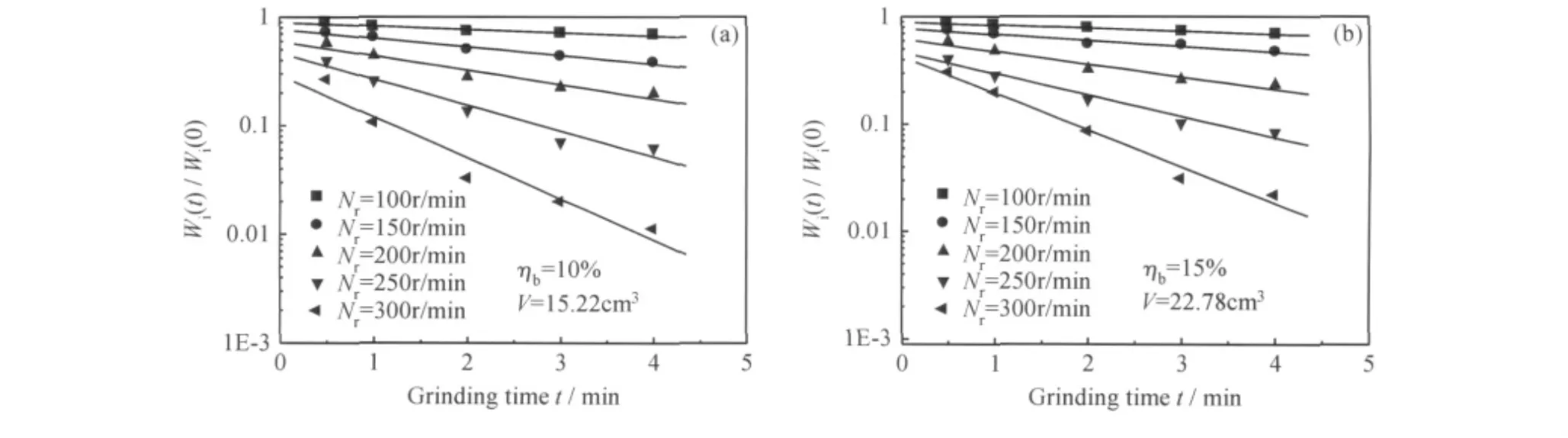
图3 行星磨中不同公转转速下的一级粉磨动力学描述 （a）ηb＝10%；（b）ηb＝15%Fig.3 First－order plots with different revolution speed in planetary ball mill （a）ηb＝10%；（b）ηb＝15%

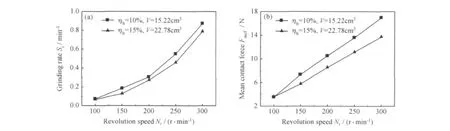
图4 行星磨中公转转速与粉磨速率和平均接触力的关系 （a）粉磨速率；（b）平均接触力Fig.4 Relation between the grinding rate，mean contact force and the revolution speed（a）grinding rate；（b）mean contact force

图4（b）是磨筒内钢球平均接触力Fmcf与公转转速Nr之间的关系，在一定的ηb条件下钢球的平均接触力随着公转转速Nr的增加而增加，平均接触力Fmcf和粉磨速率Si相关，两种填球率下的数据作出了图5，纵坐标粉磨速率设置为对数坐标，横坐标是平均接触力，从图5可以看出Fmcf和lgSi呈线性关系，对两组数据进行拟合，得到如图5所示直线，由此可构建Fmcf和Si的关系，如方程（4）所示。

式中：常数A为0.039；k为0.087。

由方程（4）可知，本实验中卧式行星磨的粉磨速率可由平均接触力确定。

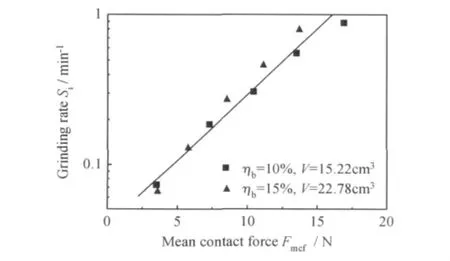
图5 行星磨中平均接触力与粉磨速率的关系Fig.5 Relation between the grinding rate and the mean contact force

4 离散元模拟结果与讨论

4.1 填球率对钢球运动规律的影响

卧式行星磨运转时，磨筒内钢球与钢球相互碰撞，钢球在磨筒内的运动规律受彼此影响，也受磨筒内钢球可运动空间大小的影响，填球率ηb势必会影响钢球运动空间及钢球间的相互作用。在磨筒自转公转转速比r＝1.5，公转速度为300r/min，磨筒内钢球直径为12mm时，模拟了填球率在5%～35%之间钢球的运动状态，如图6所示，随着填球率的增加钢球之间的空隙越来越小。

图6 磨筒填球率对钢球运动状态的影响Fig.6 Kinestate of the grinding balls under different ball filling ratio

图7（a）是公转转速分别为200，300，400r/min条件下，填球率ηb对平均接触力Fmcf的影响规律曲线，可以得知随着填球率ηb上升，平均接触力Fmcf值逐渐减小，开始阶段下降速度快，随后逐渐变缓，在公转转速300r/min条件下，填球率ηb为5%和35%对应Fmcf值分别是20.16N和6.68N。钢球的平均接触力Fmcf可以由方程（5）给出：

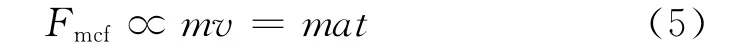
式中：m是钢球质量；v是钢球碰撞时的速度；a是作用在钢球上的加速度；t是钢球在磨筒内运动的时间。随着填球率ηb的增加，钢球运动空间变小，钢球在磨筒内运动时间t减少，所以Fmcf减小。

图7 磨筒填球率（a）和钢球直径（b）对平均接触力的影响Fig.7 Relation between the ball filling ratio（a），ball diameter（b）and mean contact force

4.2 钢球直径的放大

磨筒填球率为15%保持不变，磨筒为2号筒（半径44.5mm），转速比r＝1.5，钢球直径变化范围为10～20mm，每次增加幅度为2mm。公转转速分别为200，300，400r/min的条件下，钢球直径对平均接触力Fmcf影响规律如图7（b）所示，可以看出平均接触力Fmcf与钢球直径呈线性关系，以公转转速Nr＝300r/min为例，斜率为2.5，钢球直径10mm 时，Fmcf值是8.9N，16mm时是23.49N，20mm 时是33.37N，钢球直径增加1倍，Fmcf值增加3倍左右。钢球的平均接触力Fmcf与钢球质量m和时间t的关系如式（6）所示。

随着钢球直径变大，钢球质量增加，但是磨筒内钢球的运动空间变小，钢球在磨筒内运动时间t减少，两个因素共同影响，其中前者起主要作用，得出平均接触力Fmcf逐渐增加。磨筒内钢球抛落状态如图8（a）所示，钢球直径增加，钢球的数量变少。

4.3 磨筒半径的放大

图8（b）是磨筒半径分别是32，56mm时磨筒内钢球的运动状态，磨筒变大，钢球相对变小，钢球的运动空间增大。

公转半径为140mm，钢球直径为12mm，为了保证衬板之间距离不变，衬板数量随着磨筒半径的增加按比例增加。公转转速分别为200，300，400r/min，变化规律如图9（a）所示，随着磨筒半径增加平均接触力Fmcf呈线性增加，以公转转速300r/min为例，斜率为0.14，磨筒半径是32mm时，Fmcf值是11.46N，半径是56mm时Fmcf值为14.81N。钢球的平均接触力Fmcf与钢球在磨筒内的运动时间t的关系如式（7）所示。

随着磨筒半径增大，磨筒内钢球的运动空间变大，钢球在磨筒内运动时间t增加，所以钢球的平均接触力Fmcf也会增大。

图8 钢球直径（a）和磨筒半径（b）对钢球运动状态的影响Fig.8 Kinestate of the grinding balls under different ball diameter（a）and pot radius（b）

4.4 公转半径的放大

磨筒半径为44.5mm，公转半径R在140～240mm之间，间距为20mm。图9（b）是公转转速分别为200，300，400r/min的三组实验，可以看出，平均接触力Fmcf随着公转半径的增加呈线性增加，以公转转速300r/min为例，斜率约为0.03，公转半径是140mm时，Fmcf的值是13.26N，公转半径是240mm时Fmcf值为15.94N。钢球的平均接触力Fmcf与公转半径R关系如式（8）所示。

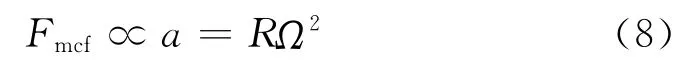
平均接触力Fmcf与公转半径R呈线性关系，所以随着公转半径的增大，钢球的平均接触力Fmcf逐渐增加。

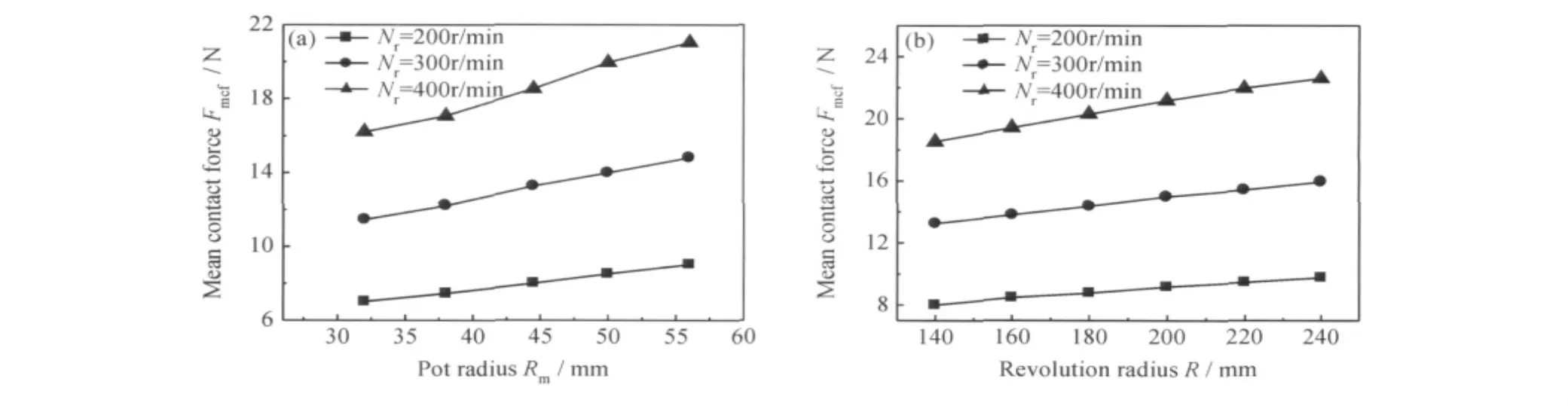
图9 磨筒半径（a）和公转半径（b）对平均接触力的影响Fig.9 Relation between pot radius（a），revolution radius（b）and mean contact force

5 结论

（1）平均接触力Fmcf和粉磨速率Si有密切关系，lgSi和Fmcf呈线性函数关系，行星磨的粉磨速率可以由平均接触力Fmcf来确定。

（2）随着磨筒填球率的增加，钢球的平均接触力Fmcf逐渐减小，减小速度开始阶段较快，随着填球率的进一步增大下降趋势逐渐变缓。

（3）钢球平均接触力Fmcf随着钢球直径的增大而逐渐增大，两者呈线性关系，公转转速是300r/min时斜率为2.5。

（4）钢球平均接触力Fmcf分别与磨筒半径、公转半径呈线性增长关系，公转转速是300r/min时斜率分别为0.14和0.03。

［1］吴光瑞，张林进，叶旭初.卧式行星球磨机粉磨水泥熟料的试验研究［J］.中国粉体技术，2010，16（6）：39－43.

［2］颜景平，易红，史金飞，等.行星式球磨机研制及其节能机理［J］.东南大学学报：自然科学版，2008，38（1）：27－31.

［3］颜景平，党根茂.行星式球磨机最佳参数的理论分析［J］.电子工业专业设备，1990，12（3）：47－51.

［4］CUNDALL P A ，STRACK O D L.A descrete numerical model for granular assembles［J］.Geotechnique，1979，29（1）：47－65.

［5］KANO J，HIROSHI M ，SAITO F.Correlation of size reduction rate of inorganic materials with impact energy of balls in planetary ball milling［J］.Journal of Chemical Engineering of Japan，1999，32（5）：445－448.

［6］KANO J，HIROSHI M ，SAITO F.Correlation of grinding rate of gibbsite with impact energy of balls［J］.A I Ch E Journal，2000，46（3）：1694－1697.

［7］HIROSHI M ，KANO J，FUMIO S，et al.Effects of rotational direction and rotation－to－revolution speed ratio in planetary ball milling［J］.Materials Science and Engineering A，2002，332（1－2）：75－80.

［8］HIROSHI M ，KANO J，FUMIO S.Scale－up method of planetary ball mill［J］.Chemical Engineering Science，2004，59（24）：5909－5916.

［9］SATO A，KANO J，SAITO F.Analysis of abrasion mechanism of grinding media in a planetary mill with DEM simulation［J］.Advanced Powder Technology，2001，36（2）：212－216.

［10］朱飞，张林进，蔡道林，等.颗粒离散元法模拟卧式行星球磨机

内钢球的运动规律［J］.矿山机械，2011，39（4）：55－59.

Simulation of Optimum Parameter in Horizontal Planetary Ball Mill

ZHU Fei，ZHANG Lin－jin，CAI Dao－lin，YE Xu－chu
（State Key Laboratory of Materials－Oriented Chemical Engineering，College of Materials Science and Engineering，Nanjing University of Technology，Nanjing 210009，China）

采用颗粒离散元法模拟得到卧式行星磨磨筒内钢球平均接触力大小以及随填球率、钢球直径、磨筒半径和公转半径的变化规律，并与实验结果进行了比较分析。结果表明：行星磨的粉磨速率可以由平均接触力大小来确定，粉磨速率的对数是平均接触力线性函数，斜率为0.087。磨筒填球率的增加，导致钢球的平均接触力减小；随着钢球直径、磨筒半径、公转半径的增大，平均接触力呈线性增长，斜率分别为2.5，0.14，0.03，其中钢球直径对平均接触力的影响最大。

粉磨速率；数值模拟；卧式行星球磨机；离散元法

Simulation of the mean contact force of grinding balls in the horizontal planetary ball mill and relation between the mean contact force and factors including ball filling ratio，grinding ball diameter，milling pot radius and revolution radius were done using the distinct element method for particle system，and with the experimental results for comparative analysis.The results show that the grinding rate of the horizontal planetary ball mill can be determined by the mean contact force，logarithm of the grinding rate is linear function about the mean contact force and the gradient is 0.087.With fill rate increasing，the mean contact force of grinding balls decreases gradually；the mean contact force of grinding balls increases linearly with the grinding ball diameter，milling pot radius and revolution radius，and the gradient is 2.5，0.14and 0.03respectively，the grinding ball diameter is primary factor，meanwhile.

grinding rate；numerical simulation；horizontal planetary ball mill；distinct element method

TQ172.6＋3

A

1001－4381（2012）05－0010－05

国家重点基础研究发展计划（2009CB623100）

2011－05－12；

2012－03－26

朱飞（1985－），男，硕士，助理工程师，主要从事粉体材料、颗粒离散元模拟等方面的研究，联系地址：合肥市包河区望江东路60号合肥水泥研究设计院（230051），E－mail：zhufly854@126.com