高速公路收费问题
——一个源于交通博弈的分析
吴万宗汤学良
(1.上海大学 社会科学学院,上海200444;2.上海财经大学 经济学院,上海200433)
高速公路收费问题
——一个源于交通博弈的分析
吴万宗1汤学良2
(1.上海大学 社会科学学院,上海200444;2.上海财经大学 经济学院,上海200433)
当个体考虑驾车到达某地或者是从互联网上传输数据,都会涉及到最基本的博弈思想:人们不是简单的选择一条线路,而是需要去评估那些由他自己和其他人所做的决策引起的线路阻塞问题。[1](P229-247)一旦个体是理性的参与人,他们的最终决策会达到我们通常所说的纳什均衡解处。但是,令人吃惊的是,为了提高运力而增加的额外道路,不但没有提高交通运输能力,反而是减少了,这个结果被称之为Braess悖论。显然,它是一个坏的纳什均衡。于是,为了解决这一难题,高速公路的收费有时候看起来就不是那么令人讨厌的了。
纳什均衡;Braess悖论;高速公路;收费
一、问题的提出
本文用一个有向图来表示一个交通网络:考虑用线条表示高速公路,而节点则表示出入特定高速公路的枢纽。例如,假设A为一个郊区枢纽,B为一个市区枢纽,我们正在关注一个早班车辆的行驶数据。统计结果是,每一条路段都会有一个特定的取决于其承载车辆多少的行驶时间。
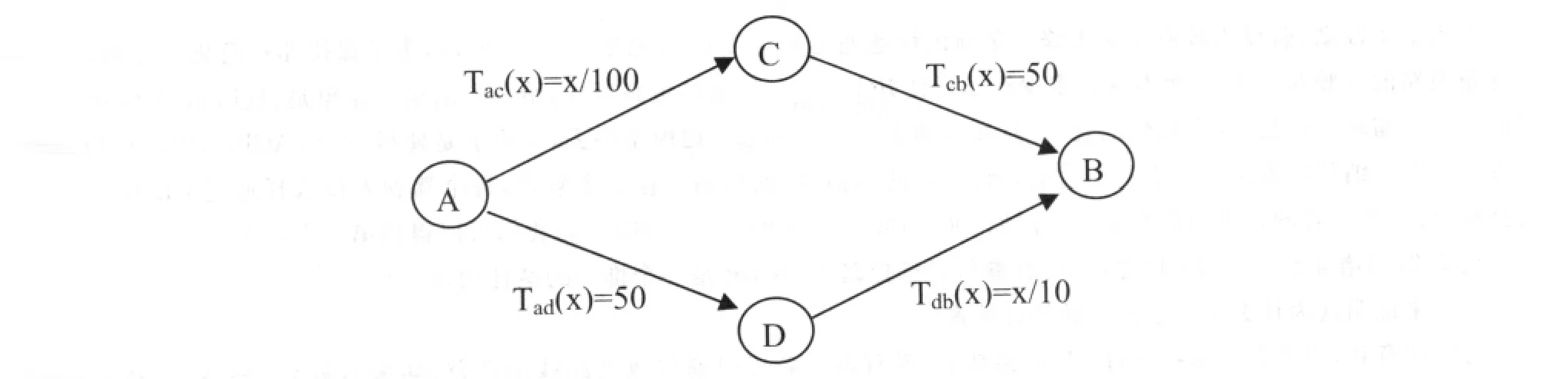
图1
为了使问题更加具体,考虑图1中的交通网络,网络可以是任何一个有向图。有一个驾驶人员的集合,并且不同的驾驶人员可以有不同的起始点和目的地。现在,每条路段e具有一个行驶时间函数Te(x),它给出了当有x名驾驶人员行驶在该路段上,个体穿越路段所需时间是Te(x)。这些行驶时间是用简化的函数来表示的,假设所有行驶时间函数是依据交通量而线性的,所以Te(x)=Ae·x+B,其中Ae、B为系数,并且有Ae、B>0。
在这个简化的例子中,路段AD和CB对阻塞不敏感:一方面,每辆车只需50分钟即可行驶全程而不管有多少车辆在这一路段上;另一方面,路段AC和DB却对阻塞非常敏感:对于每辆车来说,当有x辆车行驶在此路段上时,将花费他(她)x/100分钟的时间去完成这一路段。①为使推理清晰,在任何现实应用中,我们可以简化行驶时间,即每条公路本应该具有最小行驶时间和对行驶其上车辆数的一个敏感时间。但是,指定路段上行驶时间的分析有助于更加直接适应错综复杂的运行。
现在,假设作为早班车辆队伍中的一部分,有4000辆车想从A地到B地。这里有两条可能的路线供每一个驾驶人员去选择:途径C的上行路线,或者是途径D的下行路线。假若每个驾驶员选择了上行路线,那么总的个体行驶时间为90分钟,因为4000/100+50=90;对于全体都选择下行路线来说是同样的。另一方面,若车辆被平分两队,分别从上、下两条路线行驶,以便每条路线仅承载2000辆车,这样对于两条路线上的人们来说每人只需花费70分钟,明显好于上述两条路线。
上面描述的交通模型可以进一步的用博弈论的语言加以刻画。[2]记4000名驾驶人员为参与者的有限集合N,N=4000。称非空集Si为参与人i∈N的策略集合,参与人在策略集合里选择任一策略Si,我们知道对于任意参与人来说,显然该交通模型中的Si={ACB,ADB}。而每个参与人最终的选择则取决于他们共同的决策,是一个时间数值的负值(因为大的行驶时间非常糟糕)。当然,在这里我们只谈论中一些纯策略的博弈,对于混合策略的概念则暂不讨论,并且这些谈论满足博弈论一些严格且有趣的假设。例如,有限理性、共同知识、完全信息等。通过以上的设定,我们可以立刻得到一个有关该交通博弈的结论:
结论1:假若参与者平均分布在两条路线上去抵达目的地,则该交通博弈达到一个纳什均衡。
为什么参与者平均分布在两条路线上可以导出一个纳什均衡,为什么所有的纳什均衡会是一个平均分布。简单地证明一下:对于第一个问题,我们仅需考虑在参与者平均分布在两条路线上之后会不会有参与者做出改变即可。我们可以看出,对于所有参与者来说改变路线的成本会更大(支付变小),所以没有参与者愿意做出改变,所以现在的状况对他们来说就是最好的,此时是一个纳什均衡。而对于第二个问题,考虑这样一个策略组合:有x名参与者使用上行路线ACB,剩下的4000-x名参与者选择下行路线ADB。假如x≠2000,那么两条路线之间会有不同的行驶时间,并且任何一位在较慢路线上的参与者将会有足够的动力去转移到更快的路线上去。进一步讲,我们得到x≠2000的策略组合不可能成为一个纳什均衡,并且那些任一x=2000的组合会是一个纳什均衡。
在图1中,每件事情都非常清晰地运作着:所有驾驶人员的理性行为带来了均衡,促使他们完美地平衡选择两条可用的路线。但是,假如在该模型上做一个小小的改变,会立即发现一个违反我们直觉的事实。

图2
作出如下改动:假设市政府决定去修一条新的快速通道来连接C、D两地,如图2所示,为了保持那种简化的分析,我们定义这条道路的行驶时间为0,而不管有多少汽车行使其上。②虽然这样对结果的影响大于使用更加现实的行驶时间,但是这种影响很小。一旦新的道路修成,给人们的第一印象是:这时从A地到B地所用的时间会缩短。可是,令人吃惊的是,一旦加入新的高速通道到交通模型中去,实质上是使得Si={ACB,ADB,ACDB}。对于得到的惟一纳什均衡是一个更长的时间,所以是一个更加坏的均衡。在均衡解处,每个驾驶人员选择通过CD这一新路段的路线,每个参与者的行驶时间都是80分钟(4000/100+0+4000/100=80)。即我们可以得到第二个结论:
结论2:当增加新的路段CD之后,所有参与者选择路线ACDB是一个惟一的纳什均衡。③这里隐含了CD为单行道的假设,即人们只可从C向D行驶。实际上,即使CD为双向道,我们仍然可以得到该结论,因为路线ADCB需要花费100分钟,这是一个严格劣策略。
接下来证明这为什么是一个惟一的纳什均衡。
可以注意到,当所有人选择通过CD的路线后,没有参与者可以通过改变路线来获益:如果回避CD路线,选择上行或者下行路线,都将花费90分钟。再考虑它为什么是惟一的均衡解。我们也可以发现,在C、D间建立的这一条道路实际上是让通过CD这条路段成为所有参与者的一个占优策略。换句话说,一旦CD路段被建立,就会像一个魔盒将所有参与者吸过来,并损害了所有人的收益。
这种通过增加网络运力却破坏完美均衡的现象被Dietrich Braess于1968年首次明确提出,后来成为著名的Braess悖论。[3]如同许多违反常理的异象一样,它需要复杂的条件合成才会突然出现;但是,这个悖论已经在一些现实中被观测到——韩国首尔,通过将一个六车道的高速公路改造成停车场,不但没有增加交通阻塞,反而比先前更加畅通。看上去,这更加像从反面佐证了Braess悖论。[4]
研究人员正在考虑Braess悖论是如何发生的。用博弈理论来讲,实际上在说明增加一个新策略的设置,会使每个人的状况变得更差而已。一个著名的例子就是囚徒困境(prisoners’dilemma):比较每个囚徒面对的可选策略只有“不坦白”,将“坦白”策略加入博弈,使得每个囚徒的境况变得更加糟糕,从而有利于审判,这也是为什么警长会这么做的原因。[1](P229-247)
然而,从直觉层面上来说,我们所有人会有一种美好的感觉,“升级”一个网络意味着一个更加美好的事情将要发生,所以当“升级”使事情变得更加糟糕之时,便令所有人感到吃惊了。
实际上,Braess悖论只是有关交通博弈问题中一大堆工作的开始。人们可以保有疑问,在新加入一条路段之后,均衡时间能够扩大多少?它与原来的均衡又有多大联系?交通网络可不可以是任意的,这些问题或已经得到解决,或有待研究。但是,本文所要考察的却是通过这一悖论所引出的有关现实中的一个看似完美解决这一悖论的措施——在高速公路上安放收费站,似乎可以阻止那种令人惊讶的坏的均衡发生。
二、均衡处的社会成本
我们试着去量化一下,最优的社会成本和均衡时的社会成本究竟有多大差距?而社会成本TSC(Total Social Cost)在该模型中被定义为所有使用道路的驾驶人员行驶时间的总和。
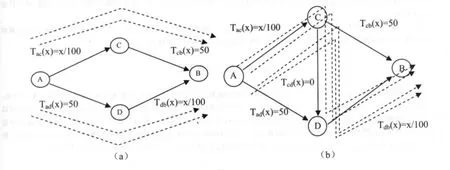
图3
先来看图3(a),这时候所有4000名驾驶人员(从A地到B地)的理性选择使得车流平分为上下两条路径,各路径上分别有2000人。在图3(a)中导出了最小的社会成本,当然,此时的社会福利也就是最大化的,每一位驾驶人员都需花费70分钟去到达目的地。所以总的社会成本是TSC1=70*4000=280000分钟。
再来看图3(b),这时候4000名驾驶人员均会选择ACDB这一“之”型的路线,因为这是他们的占优策略,而每一位驾驶人员的行驶时间为80分钟。在图3(b)中,纳什均衡处的社会成本TSC2=80*4000=320000分钟。我们还知道的事实是,在图3(b)中,280000分钟是最优的社会成本,但却没有被得到。
很明显,TSC2>TSC1,这从社会成本的角度再次印证了Braess悖论的发生,所以,当加入一个新的路段到交通博弈中去时,坏的均衡是可能发生的。现在,我们考虑收费站T伴随新路段CD的加入而加入。为了得到完美地结果,或者说更加贴近现实,需要对以上分析的博弈稍加修改,这种修改也只是限于假设层面。
三、收费站的设置
现在改变一些假设,参与博弈的驾驶人员(从A地到B地)被平分成这样的两类人:一类是优先考虑行驶的时间成本,另一类是首先考虑金钱成本。当我们计算社会总成本的时候仍然以行驶时间为参照,即时间与金钱暂不考虑可以互相转化。当然我们是在摒弃燃油费、建立路段CD和收费站T的成本的条件下再次审视这个博弈。
这时候,我们再来考虑这个交通博弈,均衡会是什么呢?社会最优解处的成本与博弈均衡解处的成本又有怎样的差异?

图4
我们可以从图4看出,在均衡处,一类驾驶人员会为了节省过路费而选择相对便宜的上下路径,且这2000人会平均分布在ACB和ADB路线上,每个人花费3000/100+50=80分钟;而另一类驾驶人员,他们则不顾收费站的存在选择占优策略——ACDB“之”字型路径,每个人花费3000/100+0+3000/100=60分钟。
现在我们再来看看均衡处的社会总成本TSC=80*2000+60*2000=280000分钟,这与我们最初考察的社会最优成本是一致的。所以,我们可以得出结论:
结论3:在新路段加入时,配套的收费系统可以有效地防止Braess悖论发生,可以使那个坏的纳什均衡不出现,此时社会福利是最优的。
所以,在我们衡量政府一个措施出台或者是规制的效果时,不能单单的考量其表面的一些数据,还应看看其背后隐藏的许多其他要素间的相互影响,这也是博弈论在当代分析工具领域所具有的独特魅力所在。
四、本文的启示与不足
本文的假设都是为了得到最终的结果。例如,对路段时间函数的设立,两类人的平均概率分布,时间与金钱不相互转化,还有交通均衡的纳什均衡解是否存在,如何寻找的问题。这都是我们必须要进一步深入探讨的,如果放松上述条件仍然可以得到一个一般性的结论,那么就是说我们可以有效解决Braess悖论。但是,本文只是为了说明一个问题:当人们总是在讨论公路收费问题是如何糟糕的时候,通过其背后隐藏的信息,有时候那些看似坏的规制并不总是很糟糕。所以,本文使用一些很强的假设足矣去说明一个问题:当前形势下的一些道路收费政策,如果我们从博弈的视角看,是有其合理性的。
[1]David Easley ,Jon Kleinberg.Networks.Crowds,and Markets:Reasoning about a Highly Connected World [M].Cambridge University Press,2010.
[2]〔加〕马丁.J.奥斯本,〔美〕阿里尔·鲁宾斯坦.博弈论教程[M].魏玉根,译.高峰,校.北京:中国社会科学出版社,2000.
[3]Dietrich Braess.Uber ein paradoxon aus der verkehrsplanung[J].Unternehmensforschung,1968,(12).
[4]Linda Baker.Removing roads and traffic lights speeds urban travel [J].Scientific American.2009,2.
吴万宗(1986-),男,上海大学社会科学学院政治经济学2010级硕士研究生,主要从事公共经济学、社会主义经济理论研究;汤学良(1986-),男,上海财经大学经济学院经济学2011级博士研究生,主要从事博弈理论、宏观经济理论研究。

