大跨度CFRP缆索悬索桥的抗风稳定性能

李 扬，肖汝诚

（1.同济大学 桥梁工程系，上海 200092；2.上海市政工程设计研究总院（集团）有限公司，上海 200092）

近年来随着经济的飞速发展，桥梁建设已经逐步进入了建造跨海大桥的新时代［1－3］.传统钢缆索悬索桥的主缆自重过大降低了悬索桥的跨越能力，使得结构承载效率低下.相对于钢材，CFRP（carbon fiber reinforced polymer，碳纤维增强塑脂）材料具有轻质高强的特点，并且抗腐蚀性能很好，因此成为未来替代钢材作为主缆材料的最佳选择［4－5］.然而相对于传统悬索桥，CFRP缆索悬索桥的结构更为轻柔，因此抗风稳定性往往成为控制设计的重要因素之一.其失稳模式主要包括静风失稳和颤振失稳［6－7］.

方明山［8］曾对主跨为2000～4000m的CFRP缆索悬索桥进行了静风稳定性能研究，认为采用CFRP缆索后静风失稳临界风速将有所降低；张新军等［9－10］对 主跨为1400m 的CFRP缆索悬索桥颤振性能进行了研究，认为采用CFRP缆索后由于扭转基频提高使得颤振临界风速有所提升，并且建议利用“等刚度原则”设计CFRP缆索以获得更好的抗风性能，但在大跨度条件下采用这一原则会造成缆索材料的浪费；郑宏宇［11］利用简化计算公式定性地讨论了2000m级悬索桥的抗风稳定性，认为采用CFRP缆索后结构的静风稳定性将减弱而颤振性能则相差不大.针对传统钢缆索悬索桥的抗风问题，项海帆等［12］、杜柏松［13］，以及日本学者 Koichiro等［14］分别通过数值和试验的方法研究了悬索桥的不同断面类型，得到了气动力特性更为优越的一些断面形式，如中央开槽箱梁、分体双箱梁等；马如进等［15］认为在吊索吊点间设置一些拉索可以提高悬索桥的扭转基频，从而提高临界风速.然而，CFRP缆索悬索桥本身的抗风性能能否满足设计要求，传统悬索桥的气动措施对此类悬索桥的效果如何，对于不同的跨径条件，选择怎样的抗风措施能使结构方案成立，这些问题都有待研究解答.

为此，本文利用基于非线性有限元的抗风稳定计算方法对主跨2000～5000m的大跨度悬索桥进行了对比研究，然后对CFRP缆索悬索桥的一系列抗风措施进行了有效性验证，并总结出相应的设计建议.

1 悬索桥非线性抗风稳定分析方法

1.1 非线性静风稳定分析方法

静风失稳是指结构在给定风速作用下，主梁发生弯曲和扭转，使得风荷载和结构刚度均发生改变，又进一步增大结构的变形，最终导致结构失稳的现象.

1.1.1 非线性静风荷载描述方法

静风对主梁的作用可由气动三分力（升力、阻力和升力矩）来描述［8］，其表达式如下：

式中：FD，FL和FM分别表示来风在主梁上引起的气动阻力、气动升力和气动升力矩作用；ρ表示空气密度；V为桥面高度处的风速；α是有效风攻角；H，B分别为主梁的高度和宽度；CD，CL和CM称为气动三分力系数，可由阶段模型风洞试验或者数值模拟方法获得.

1.1.2 非线性静风失稳的机理

结构的静风失稳过程如图1所示［16］.图中：R1表示结构刚度不变；R2表示结构刚度受变形影响后非线性减小；W1表示静风荷载随风速平方值线性增大；W2表示静风荷载受到结构变形影响后非线性增大；A点表示不考虑结构变形影响时的失稳点，对应临界风速为V2；B点表示仅考虑结构变形对结构刚度非线性影响时的失稳点，对应临界风速为V1；C点表示同时考虑结构变形对静风荷载和结构刚度的非线性影响时的失稳点，对应的临界风速为Vlb.由图可知，Vlb远小于V1和V2，可见Vlb是真正的失稳临界风速.

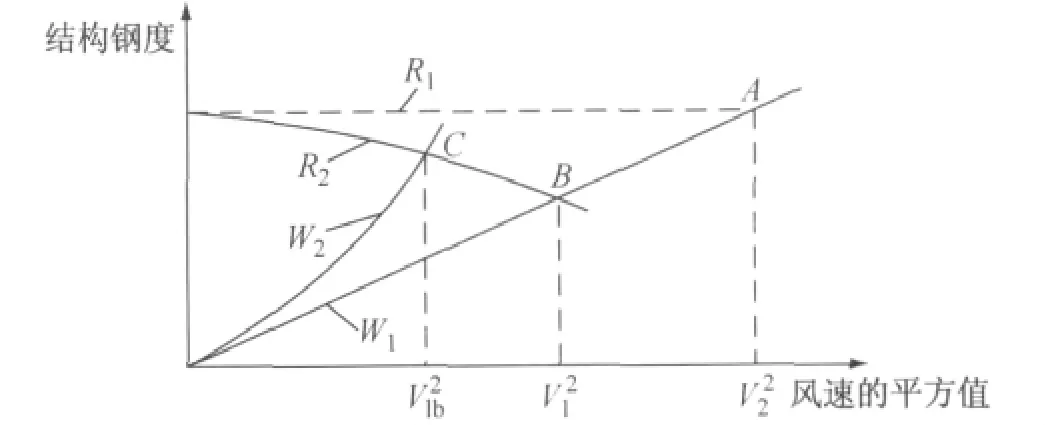
图1 结构静风失稳过程示意图Fig.1 Aerostatic instability process

1.1.3 非线性静风稳定的有限元分析步骤

①建立空间有限元模型，确定悬索桥成桥状态；

② 选定初始风速V0和风速增量ΔV，并令当前风速Vi＝V0；

③ 提取初始风攻角α0对应的三分力系数Ck，0（下标k表示三分力方向D，L，M），计算并施加初始静风荷载F0，并进行全桥几何非线性分析；

④ 提取主梁扭转角θi，更新风攻角αi＝α0＋θi，按照更新后的风攻角提取新的三分力系数Ck，i；

⑤ 重新计算静风荷载Fi，用该静风荷载替换上次施加的Fi－1，并进行全桥几何非线性分析；

⑥提取新的主梁扭转角，并检查扭转角差值向量的欧几里德范数是否满足以下条件：

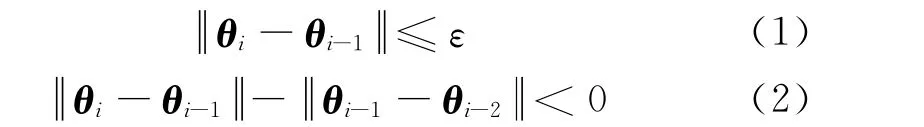
⑦ 若式（1）成立，则输出当前风速值和结构响应，然后增加风速Vi＝Vi－1＋ΔV，重复③—⑥步；若式（1）不成立，而式（2）成立，说明范数结果趋于收敛，重复④—⑥步直至式（1）成立；

⑧ 若式（1）和式（2）均不成立，说明范数结果趋于发散，则回复上一步风速，缩小风速增量步长ΔV，重复④—⑥步直至两次相邻的风速差值小于某一容许值；

⑨绘制结构响应随风速变化的全过程曲线，判定静风稳定临界风速.

1.2 非线性颤振稳定分析方法

颤振是一种气动失稳现象.处于风场中的振动结构和气流之间会因气弹效应而发生能量交换，当风速超过临界风速时，结构从气流中吸取的能量将大于阻尼所消耗的能量，从而使振动发散.

1.2.1 自激力的描述方法

颤振从本质上说是由结构与风流之间的气弹效应引起的，因此作用在结构上的自激力与其自身的运动状态有关.自激力的表达形式多样，对于钝体断面，目前最常用的是如下采用Scanlan气动导数表示的形式［17］：

式中：D，L和M 分别表示作用在单位长度结构上的气弹自激阻力、升力和扭矩；K为折算频率，K＝Bω／V；ω是振动圆频率；和为各类气动导数，是折算频率K的函数；p，h和α分别是结构的水平、竖向和转角位移.

当利用杆系有限元方法进行分析时，式（3）表述的自激力可转化为作用于单元e两节点的等效自激力

式中：Fse，e为单元e的等效节点力向量；δe和分别表示单元e两节点的位移和速度向量；Kse，e和Dse，e分别为单元e的气动刚度矩阵和气动阻尼矩阵，它们的表达式分别为［18］

式中：Le表示单元长度，其余符号意义同前.

1.2.2 气动矩阵的实现

为了在有限元程序中方便地模拟气动矩阵，在建模时可令所有主梁单元的长度相等.图2为任意一个主梁单元e，其端部节点编号为i，j；e1和e′1是两个弹簧单元，e2和e′2是两个阻尼单元，它们均一端固定，另一端与桥面单元共用同一节点［19］.

图2 桥面、弹簧和阻尼单元示意图Fig.2 Elements of deck，spring and damping

若令所有弹簧单元的刚度矩阵为Ke1＝Ke′1＝－2Kse，e，阻尼单元的阻尼矩阵为 De2＝De′2＝－2Dse，e，则对整个主梁组装后即可得到主梁承受的节点力向量为

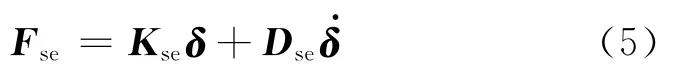
式（5）与式（4）一致，说明当主梁各单元长度均相同时，可在每个主梁节点处分别添加一个弹簧单元和一个阻尼单元，相应的刚度矩阵和阻尼矩阵分别为－2Kse，e和－2Dse，e，如此便可方便地实现对气动矩阵的模拟.

1.2.3 非线性颤振稳定的有限元分析步骤

由式（4）可以看出，由于气弹效应影响，结构的自激力与其自身的振动频率ω有关，而反过来ω又与自激力有关，仍是未知数，因此需要进行迭代求解.颤振稳定的有限元分析步骤如下：

①建立带有刚度矩阵和阻尼矩阵单元的空间有限元模型，确定成桥状态；

② 假定或修正搜索风速V，以及初始振动频率ω0；

③ 根据折算风速V／fB（其中f为结构自振频率）提取断面的颤振导数，并由此确定单元上的刚度矩阵和阻尼矩阵；

④给予结构一个初始激励（如跨中位移、速度或加速度等），进行瞬态分析；

⑤ 提取结构的振动频率ω1，若｜ω1／ω0－1｜小于某一容许值，则进入下一步；否则令ω0＝ω1，并回到步骤③；

⑥ 确定振动时程响应的对数衰减率λ，若λ＞0，增大风速V并返回步骤③；若λ＜0，减小风速V并返回步骤③；若λ＝0，输出结果，此时结构处于颤振临界状态.

本文按照上述静风与颤振稳定分析理论，基于有限元程序ANSYS的二次开发功能编制了分析程序，作为下文研究的工具.

2 钢和CFRP缆索悬索桥抗风稳定性能对比

2.1 研究对象

研究对象是一座双塔单跨悬索桥，其结构布置如图3所示.矢跨比取1／10，边中跨比为0.3.标准吊索间距取25.5m左右，边吊索至桥塔中心线距离为31m左右.

图3 悬索桥结构总体布置图Fig.3 General scheme of suspension bridge

主梁采用扁平钢箱梁，材料以Q345qD为主，截面面积为1.501m2（考虑横隔板等因素，主梁自重集度按150kN·m－1考虑），竖向抗弯惯矩为4.959 m4，侧向抗弯惯矩为90.225m4，抗扭惯矩为16.037 m4.桥塔采用混凝土桥塔，混凝土标号为C55—C60，纵向宽11.0～20.0m，侧向宽7.0～10.0m，塔柱壁厚1.8m.缆索材料的主要性能参数见表1，主缆按照强度准则设计.设计风速取100年一遇条件下的上海地区风速，并依据规范［18］计算得到静风稳定临界检验风速为84.6m·s－1，颤振临界检验风速为60.4m·s－1.

表1 缆索材料的主要性能参数Tab.1 Material property of cables

钢箱梁的三分力曲线和气动导数采用江阴长江公路大桥的实测值［16］，如图4和图5所示.

2.2 计算结果对比

表2列出了主跨为2000～5000m的钢和CFRP缆索悬索桥的失稳临界风速，以及两者之间的相差率.为了便于说明问题，表中还列出了各自的缆索线重量及扭转基频.

从表2可以看出，随着跨径的增大，悬索桥的抗风稳定性能显著降低，2000m跨径时两类悬索桥的失稳临界风速均大于临界检验风速，满足规范要求；而当跨径达到3000m级或以上时，静风和颤振失稳临界风速均低于检验风速，必须采取相应的改善措施.值得注意的是，CFRP缆索悬索桥的静风失稳临界风速低于钢缆索悬索桥，而前者的颤振临界风速却略高.这点可以通过临界风速的经验估算公式［19－20］得到解释，估算公式如下：

式中：Vlb是静风失稳临界风速；Vcr是颤振失稳临界风速；ft是对称扭转基频；Jt是桥面系及主缆单位长度的质量惯性矩；m是桥面系与主缆沿跨径的质量线密度；其余符号含义见文献［11，20］.由式（6）可知，Vlb与（即相当于）和均成正比，由表2可知主缆质量下降对静风失稳风速引起的损失大于扭转基频提高带来的贡献，因此使得CFRP缆索悬索桥的静风失稳临界风速低于钢缆索悬索桥.而式（7）则表明Vcr与和ft成正比，因此扭转基频提高对颤振失稳风速带来的贡献超过了主缆质量下降引起的损失，从而使得其颤振性能反而得到了提高.

表2 主跨为2000～5000m的钢和CFRP缆索悬索桥的抗风稳定性能对比Tab.2 Comparison of aerostatic stability of 2000～5000mlong－suspension bridges with steel and CFRP cable

应该注意的是，虽然采用CFRP缆索后悬索桥的颤振失稳风速略有提高，但提高幅度并不大，其颤振失稳问题仍十分突出.

3 改善CFRP缆索悬索桥抗风性能的措施

本文探讨的抗风措施可分为结构措施和气动措施两大类.结构措施包括：改变桥跨布置方式，设置中央扣，改变矢跨比和边中跨比，增加辅助拉索.气动措施包括：采用设置稳定板的中央开槽箱梁，采用分离式中央窄开槽或宽开槽断面.

3.1 改变桥跨布置方式、设置中央扣

以2000m跨径为例，对比设置中央扣前后的单跨、三跨CFRP缆索悬索桥的临界风速列于表3，说明桥跨布置方式和中央扣对抗风性能的影响都很小.

表3 桥跨布置方式和中央扣对CFRP缆索悬索桥临界风速的影响（2000m）Tab.3 Influence of span and central buckle to the critical velocity of suspension bridges with CFRP cable（2000m） m·s－1

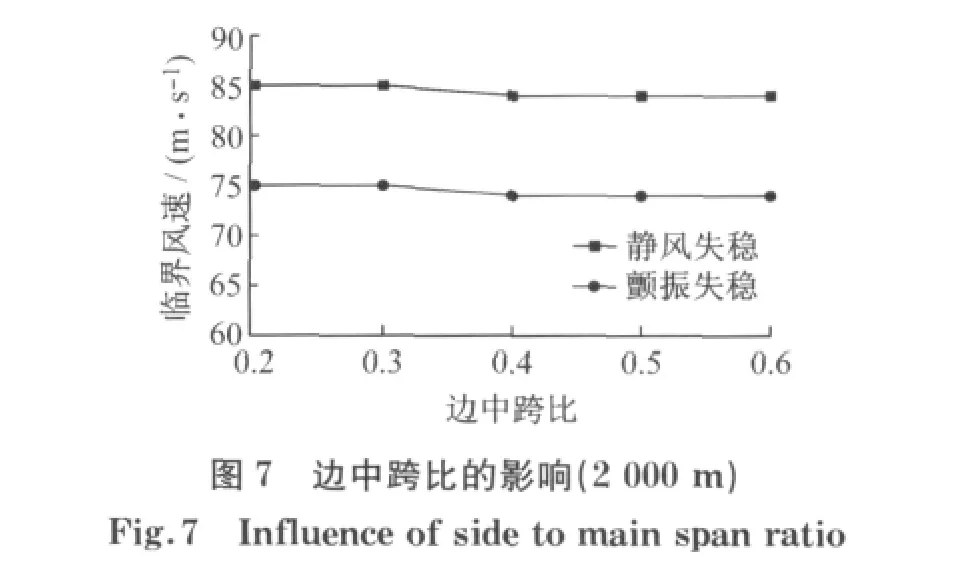
3.2 改变矢跨比和边中跨比

以2000m跨径为例，不同矢跨比、边中跨比所对应的失稳临界风速分别如图6和图7所示.可以看出：①矢跨比越小则CFRP缆索悬索桥的抗风性能也越差，这是因为矢跨比的减小会使得所需主缆面积有所增加，从而增大了主缆上的迎风面积，因此，在静力刚度允许时宜采取较大的矢跨比；②边中跨比对抗风性能的影响甚微.

3.3 增加辅助拉索

上述措施中，仅有改变矢跨比能在小范围内改善结构的抗风性能，但尚不足以使得3000m跨径以上的CFRP缆索悬索桥的结构方案成立.为了进一步提高其抗风性能，此处研究辅助拉索的作用.辅助拉索包括两种类型，即水平拉索和竖直拉索，如图8所示.

马如进［15］对于传统钢缆索悬索桥的研究成果指出，分别将两类辅助拉索布置在跨径的1／4～1／3范围内时，均能够提高结构的临界风速.本文在3000mCFRP缆索悬索桥的1／4～1／3跨径范围内同时布置这两类拉索，布置前后的临界风速分别列于表4.

表4 辅助拉索对临界风速的影响（3000m）Tab.4 Influence of auxiliary cables（3000m）

由表4可知，辅助拉索可以显著改善结构的抗风性能，这是因为辅助拉索提高了结构沿桥轴向的扭转约束，使得扭转频率显著提高，从而改善了抗风性能.设置辅助拉索后，3000m级CFRP缆索悬索桥的失稳临界风速可以满足规范要求.进一步的研究发现，对于4000m级CFRP缆索悬索桥而言，设置辅助拉索可使其静风失稳临界风速从54m·s－1提高到70m·s－1，仍低于临界检验风速.因此辅助拉索仅能使3000m级或以下的CFRP缆索悬索桥的方案成立，4000m以上跨径的悬索桥尚需要采取其他更为有效的抗风措施.

3.4 采用设置稳定板的中央开槽箱梁

一些研究指出，在加劲梁的中央开槽并设置中央稳定板可以减小气动力.本文采用日本学者Koichiro提出的开槽箱梁［14］进行研究，稍加修改后的断面如图9所示.箱梁尺寸与前文基本相同，不同之处在于前文箱梁宽度为36m，此处需加上中央开槽宽度2.8m，即总宽为38.8m.桥面上方设置3条稳定板，包括1条中央稳定板和2条侧边稳定板.

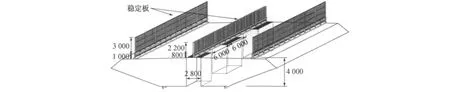
图9 带稳定板的中央开槽箱梁示意图（单位：mm）Fig.9 Central slotted girder with guard fences（unit：mm）

气动三分力系数和气动导数采用Koichiro等［14］对该类断面研究得到的实测值，如图10和11所示.从图10可以看出，稳定板的存在使得箱梁的阻力系数增大，但是稳定板和中央槽口能够使升力系数和升力矩系数大为减小，从而削弱了箱梁所受的气动升力和升力矩.

图10 带稳定板中央开槽箱梁的三分力系数Fig.10 Aerostatic coefficients of central slotted girder with guard fences

采用图9所示箱梁前后，4000mCFRP缆索悬索桥的抗风性能列于表5.可见，采用带有稳定板的中央开槽箱梁，由于其升力系数、升力矩系数以及气动导数较小，从而使得4000m级CFRP缆索悬索桥的抗风性能大为提高，达到了规范要求.但由于超过临界检验风速的量值并不大，因此还可断定，对于5000m跨径的CFRP缆索悬索桥，采用这种开槽箱梁仍是不够的.

3.5 采用分离式中央窄开槽或宽开槽断面

图11 带稳定板中央开槽箱梁的气动导数（0°风攻角）Fig.11 Aerodynamic coefficients of central slotted girder with guard fences（0°）

表5 采用中央开槽箱梁对临界风速的影响（4000m）Tab.5 Effect of central slotted girder to the critical velocity（4000m）

为了进一步提升悬索桥的气动力性能，国内学者项海帆［12］等提出了双主缆带稳定板的分离式中央窄开槽方案和四主缆中央宽开槽方案，如图12所示.

图12 分离式中央窄开槽和宽开槽断面图（单位：m）Fig.12 Narrowly slotted and widely slotted section diagrams（unit：m）

本文以窄开槽断面为例，研究其对5000m跨径CFRP悬索桥抗风性能的改善作用.窄开槽断面的气动三分力系数和气动导数采用项海帆等［12］通过计算流体动力学研究获得的结果，如图13和14所示.从图13可以看出，采用窄开槽断面后，气动三分力系数均大为减小，从而使得主梁受到的气动力也显著降低.

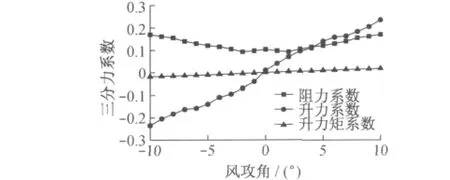
图13 窄开槽断面的三分力系数Fig.13 Aerostatic coefficients of narrowly slotted section

采用分离式中央窄开槽断面前后，5000m CFRP缆索悬索桥的抗风性能列于表6.可见，利用窄开槽断面方案，可以使结构抗风性能获得极大的提升，完全满足了规范要求.此外，进一步研究表明，相对于窄开槽断面，运用四主缆中央宽开槽断面时悬索桥的颤振稳定性能更为优越，而静风稳定性能稍差，但仍然远大于临界检验风速.

表6 采用窄开槽断面对临界风速的影响（5000m）Tab.6 Effects of narrowly slotted section（5000m）

图14 窄开槽断面的气动导数（0°风攻角）Fig.14 Aerodynamic coefficients of narrowly slotted section

4 结论

本文利用悬索桥静风稳定和颤振失稳的非线性有限元计算方法，对主跨2000～5000m的钢缆索和CFRP缆索悬索桥的抗风性能进行了对比分析，得到了如下结果：

（1）抗风失稳临界风速随着跨径增大而急速降低.主跨2000m时两类悬索桥的失稳临界风速均大于临界检验风速；而当跨径达到3000m级或以上时，则必须采取相应的改善措施.

（2）采用CFRP缆索后，悬索桥的静风失稳临界风速将降低，而颤振临界风速则略微提高.这是由缆索质量下降和扭转基频提高的综合作用引起的.

（3）尽管采用CFRP缆索后悬索桥的颤振失稳风速有所提高，但颤振检验风速本身远低于静风失稳检验风速，因此在设计时必须同时对两类抗风问题加以重视.

为了进一步提高大跨度CFRP缆索悬索桥的抗风性能，对一系列抗风措施的有效性进行了验证，得到了以下结论和建议：

（1）桥跨布置方式、中央扣、边中跨比对结构抗风性能影响很小.

（2）在常规范围内，矢跨比越小则抗风性能越差，因此在静力性能允许的前提下可采用较大的矢跨比.

（3）当主跨为3000m级或以下时，可以通过增加辅助拉索的措施使其抗风性能达到规范标准.辅助拉索包括水平拉索和竖直拉索两类，可布置在1／4～1／3跨径范围内.

（4）当主跨达到4000m级时，可以采用带有稳定板的中央开槽箱梁改善结构抗风性能，稳定板包括中央稳定板和侧边稳定板两类.

（5）对于主跨超过5000m的CFRP缆索悬索桥，则应该采用窄开槽断面或四主缆中央宽开槽断面，此时结构的抗风稳定性可获得极大的提升.

［1］Curran D J.Bridging the strait：implications for Japan and the United States following apeaceful reunification of China and Taiwan［D］.Monterey：Naval Postgraduate School，2007.

［2］CUI Jianjiang，FU Chengsong.An engineering concept of the Taiwan Strait Tunnel ［J］.Marine Georesources and Geotechnology，2004，22（3）：173.

［3］杨艳，陈宝春.世界跨海工程概况与台湾海峡通道可能性［J］.福州建筑，2007（8）：26.YANG Yan，CHEN Baochun.Development of cross strait engineering in the world and the possibility of Taiwang Strait Tunnel project［J］.Fuzhou Structure，2007，（8）：26.

［4］Meier U.Proposal for a CFRP bridge crossing the Strait of Gibraltar at its narrowest point ［J］. Proceedings——Institution of the Mechanical Engineerings，1987，201（B2）：7378.

［5］应东磊.碳纤维索在大跨度缆索承重桥梁上的应用研究［D］.杭州：浙江工业大学建筑工程学院，2008.YING Donglei.Study on the application of CFRP cables in longspan cable－supported bridges ［D］. Hangzhou： Zhejiang University of Technology.College of Civil Engineering and Architecture，2008.

［6］ZHANG Xinjun，YING Donglei.Wind－resistant performance of cable－supported bridges using carbon fiber reinforced polymer cables［J］.Wind and Structures，2007，10（2）：121.

［7］ZHANG Xinjun，YING Donglei.Aerodynamic stability of cablesupported bridges using CFRP cables［J］.Journal of Zhejiang University，2007，8（5）：693.

［8］方明山.超大跨度缆索承重桥梁非线性空气静力稳定理论研究［D］.上海：同济大学土木工程学院，1997.FANG Mingshan.Nonlinear aerostatic stability theory of superlong－span cable－supported bridges ［D］.Shanghai：Tongji University.College of Civil Engineering，1997.

［9］张新军，应东磊.应用CFRP索的缆索承重桥梁抗风稳定性研究［J］.公路，2007（7）：38.ZHANG Xinjun，YING Donglei.A study on wind stability of cable－supported bridges using CFRP cables［J］.Highway，2007（7）：38.

［10］张新军，应东磊.应用碳纤维索的大跨度悬索桥抗风稳定性研究［J］.土木工程学报，2006，39（12）：80.ZHANG Xinjun，YING Donglei.Wind stability of long－span suspension bridges using carbon fiber reinforced polymer cables［J］.China Civil Engineering Journal，2006，39（12）：80.

［11］郑宏宇.CFRP缆索悬索桥基本性能及若干关键技术研究［D］.南京：东南大学土木工程学院，2007.ZHENG Hongyu.Research on the basic behaviors and several key techniques of suspension bridge with CFRP Cables［D］.Nanjing： Southeast University. College of Civil Engineering，2007.

［12］项海帆，葛耀君.悬索桥跨径的空气动力极限［J］.土木工程学报，2005，38（1）：60.XIANG Haifan， GE Yaojun. On aerodynamic limits to suspension bridges［J］.China Civil Engineering Journal，2005，38（1）：60.

［13］杜柏松.考虑非线性影响的分体双箱梁悬索桥动力特性研究［D］.上海：同济大学土木工程学院，2006.DU Bosong.Study on dynamic characteristics of suspension bridges with twin－box stiffening girders considering geometric nonlinearity［D］.Shanghai：Tongji University.College of Civil Engineering，2006.

［14］Fumoto K， Hata K， Matsuda K， et al. Aerodynamic improvement of slotted one－box girder section for super long suspension bridge［C］／／The Sixth Asia－Pacific Conference on Wind Engineering.Seoul：Techno Press，2005：1－15.

［15］马如进，陈艾荣.辅助结构对悬索桥的颤振稳定性的影响［J］.结构工程师，2001（3）：25.MA Rujin，CHEN Airong.The influence of auxiliary structure on flutter－stability of suspension bridges ［J］.Structural Engineers，2001（3）：25.

［16］程进.缆索承重桥梁非线性空气静力稳定性研究［D］.上海：同济大学土木工程学院，2000.CHENG Jin.Study on nonlinear aerostatic stability of cablesupported bridges［D］.Shanghai：Tongji University.College of Civil Engineering，2000.

［17］Scanlan R H，Tomko J J.Airfoil and bridge deck flutter derivatives［J］.Journal of Structural Engineering，1971，116（2）：279.

［18］Namini A，Pedro A，Harold B.Finite element－based flutter analysis of cable－suspended bridges［J］.Journal of Structural Engineering，1992，118（6）：1509.

［19］华旭刚，陈政清，祝志文.在ANSYS中实现颤振时程分析的方法［J］.中国公路学报，2002，15（4）：32.HUA Xugang，CHEN Zhengqing，ZHU Zhiwen.Approach of time－history analysis of flutter in ANSYS［J］.China Journal of Highway and Transport，2002，15（4）：32.

［20］中交公路规划设计院.JTJ xxx—2002公路悬索桥设计规范（报批稿）［M］.北京：人民交通出版社，2002.CCCC Highway Consultant Co.Ltd.JTJ xxx—2002 Design specification for highway suspension bridge（draft for approval）［M］.Beijing：China Communications Press，2002.