深厚覆盖层中竖井井壁负摩阻力分析

徐 伟，陈 希，申青峰

（同济大学 土木工程学院，上海 200092）

竖井是矿山地面与地下的通道.我国华东、华北、华中、东北地区的许多矿区上覆厚表土层.在地质条件较好的矿区已被开发，但仍不能满足需求时，竖井深度已由建国初期的100m左右向700m、甚至上千m的超深方向迅速发展.在井筒施工中或矿井投产后，我国一些地区的矿井出现井壁破裂现象，成为一种新的矿井病害.井壁破裂的发生严重影响了竖井的正常运营，造成了巨大的经济损失.针对井壁破裂事故的普遍发生，建井工程界进行了大量的研究探索，在研究中发现，由于地表沉降在井壁上产生的竖向附加应力是井壁发生破裂的主要原因［1］.竖向附加应力的计算一向是工程界研究难点所在，目前尚无公认的统一公式.倪兴华［2］根据土力学基本原理先后求出地层沉降量、地层内的剪应力，并由此推出井壁临近破裂的极限状态下的竖向附加应力公式.杨维好等［3－4］基于模型试验用幂函数对黏土、砂质黏土、黏质砂土的附加应力增长率随深度变化的关系进行拟合.但上述公式研究均基于一定的条件假设，适用性及可靠性还有待验证，故研究竖井井壁的竖向附加应力有其实用价值.

含水层疏水沉降学说中的竖向附加应力多表现为作用在井壁上的摩阻力，该摩阻力多以类似于桩基工程中负摩阻力的形式出现.在含水层固结沉降的过程中，深厚覆盖层内的竖井井壁—土作用机理在一定程度上与桩—土模型相似：结构与土体之间通过接触面上的竖向摩擦力而相互作用［5］.相对于桩而言，竖井并不需要承受地面结构的竖向荷载，但其在土体中仍会有下沉的趋势，这时在接触面上（井壁），土体就会对其产生一个向上的摩阻力，即正摩阻力；若是土体沉降速度超过了竖井下沉速度，那么相对来说，在接触面上，竖井就会产生一个向上的摩阻力以阻止土体下沉.根据力的相互作用原理，此时土体将对竖井井壁有一个与竖井重力作用方向一致的摩阻力，以加快竖井的下沉速度.这个力被称为负摩阻力.显然，负摩阻力对竖井结构是不利的.

基于上述陈述，本文将利用ABAQUS有限元分析软件，对竖井井壁在含水层疏水沉降作用下的负摩阻力进行研究.在研究的过程中，作者并不关心引起底部含水层排水的原因，而是人为将排水面设置在不同的位置，从而在井壁负摩阻力分析的基础上，预测竖井周边水环境改变带来的不利影响.

1 工程概况

某水电站左岸出线的1＃，2＃竖井工程，内径均为10m，竖井总深度为488.5m.左岸竖井在高程614m和607m布置有交通联系平洞与右岸相关工程相连，将竖井分为上下两段布置，上段深度为251 m，其中覆盖层厚度为59.64～166.9m.

竖井井壁现场分段浇注，留设结构缝，混凝土标号为C35.根据钻孔取样检测，左岸竖井覆盖层由下至上，从老到新依次为古滑坡堆积体、冰川冰水堆积体和洪积堆积体.

根据地质资料在古滑坡堆积体底部为滑带，厚约1～3m，属相对隔水层，地下水位高出滑带约10 m，因此覆盖层的排水主要集中在底部的10m左右，在覆盖层底部与一衬之间铺设软式透水管，并穿过一衬基座埋设的聚氯乙烯套管与下部基岩段的排水软管相连，形成系统的排水体系.基岩段井筒排水设计以排为主，为保证围岩稳定，最大限度地减小地下水渗漏对竖井的影响，对整个基岩段竖井设置直径48mm ，长4.0m，间距3.0m，梅花形布置的系统排水孔.沿洞高紧贴基岩满布直径48mm，间排距3.0m的软式排水管网，软式排水管与排水孔连接将岩壁渗水汇至竖井底部，经交通联系平洞到左右岸上坝公路排水沟排至洞外.

2 有限元模拟

考虑到渗流计算对有限元网格划分的高标准要求，选取平面单元对竖井进行模拟.在平面模拟中，圆形断面的竖井是较难处理的，如果同时考虑2个竖井，计算难度会增加且更加不宜收敛.在这里，对2个竖井进行理想化的假设［6－7］：因在施工过程中采取了合理的分段浇筑法，在未浇筑混凝土井壁前，裸露的开挖土体面上发生的渗流不足以产生影响井壁受力的沉降，即在整个开挖过程中，渗流被认为是几乎不发生的.同时，在井壁浇筑完成后，井壁抗渗水性能非常好，没有渗漏水现象发生.在上述假设下，当一个竖井受到渗流作用影响时，另一个竖井仅可能在两井断面公切线包围的渗流面上起到有限的干扰作用，如图1阴影部分所示.一般认为，这种阻断或增加渗流途径的干扰作用是有利的.因此，在线弹性材料假设和竖井3维渗流面无限多的前提下，计算中可以只选取双竖井中一个典型的理想算例.

图1 竖井渗流相互影响作用示意图Fig.1 Interaction for seepage of adjacent shaft lining

本次模拟过程中以溪洛渡左岸2＃竖井为模拟对象，为充分考虑深厚覆盖层特殊含水层的疏水沉降影响，扩大该研究的应用范围，对原结构进行扩展分析，将深度加深为180m.因结构的对称性，可只选取一半进行计算.井深取为180m，井壁单元厚度取为井壁典型厚度1.2m，悬空边界限制节点水平位移.土体尺寸水平向（垂直于井深）为360m.因井壁已经建成，且同基岩接触良好，再加上基岩不透水、不可压缩的特性，在模型中不再建立基岩土层，土层深度同井深，沿深度方向简化为3个土层，土层特性见表1.计算模型示意图见图2，有限元模型见图3.

表1 2＃竖井上段地层简表Tab.1 Upper layer of vertical shaft lining 2

2.1 含水层疏水沉降模拟

计算中认为井壁渗水不会发生，因此模拟人工对地下水的开采活动，采用孔压边界设置的方法，在假定的人工开采面上将节点孔压设置为零，降水分析方法采用可以进行时间步控制的瞬态分析法.在计算中，共给出9种排水情况，如表2和3所示.其中x表示距井土接触面，即水平距离，y表示距离含水层顶面，即降水深度.

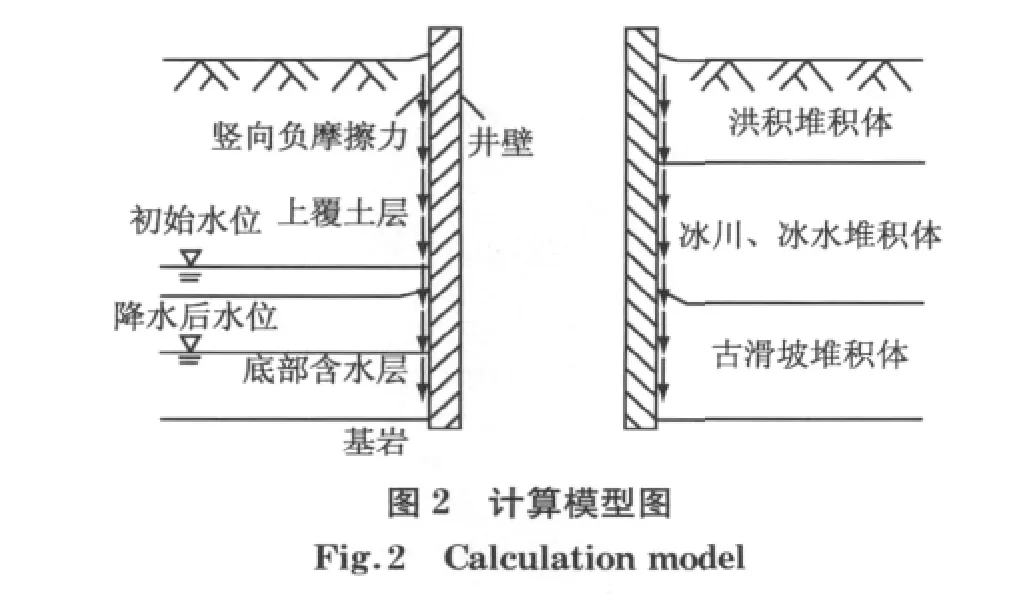
表2 假定人工排水面设置表Tab.2 Setting of artificial drainage m

表3 排水时间变化组Tab.3 Schedule of drainage

2.2 井土接触面设置

计算中采用面与面接触的指令进行分析，选择了井壁面为主面，土体表面为从属面.

2.3 计算步

加上初始分析步，总共设置3个分析步.第2步为地应力平衡步；第3步为渗流固结沉降计算步，时间总长为200d，初始步长为0.5d，除表3规定的点为排水时间即提取摩阻应力的时间外，所有的计算结果均为计算全部结束后的输出.

2.4 参数和本构

连续介质有限元计算模型根据竖井结构特点采用一半的模型进行2维分析.井壁采用周对称单元CAX4R.为了进行含水层疏水沉降的流固耦合分析，必须选用耦合单元类型，因此计算时土体选用了孔压单元CAE4RP，并采用弹性模型进行计算.

3 计算结果及分析

3.1 有限元分析结果处理

井壁自重也会产生井壁摩阻力，但这并不是本次研究的对象.软件ABAQUS提供了初始地应力平衡的方法来排除井壁自重造成的影响，使得在进行固结沉降分析前，井壁的侧壁摩阻力达到无限小的数值，不影响后续计算［8－9］.但实际上，因为考虑土体孔隙水压力的影响，和其他一些不可抗因素，初始地应力的平衡是非常困难的.如果在初始地应力平衡中不计入井土接触的影响，尽管可以达到初始摩阻力为零的情况，但是并不符合井土接触始终存在的实际情况，对土的平衡也会造成误差.若在初始平衡计算时计入井土接触的作用，仅考虑平衡土的初始位移而不考虑平衡井土接触面摩擦力，则在没有堆载、没有轴向荷载的情况下，将在固结沉降计算中所得到的摩阻力终值减去初始的摩阻力值，差值即为因渗流沉降而造成的摩阻力值，即

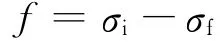
式中：f为作用在井壁上的摩阻力，数值为正则表示正摩阻力，为负表示负摩阻力；σi为土体沉降计算步骤前，竖井井壁的初始摩阻力值；σf为土体沉降计算结束后，竖井井壁的摩阻力终值.

根据上述处理原则，可得出如图4—6所示井壁摩阻力分布图.图4为同一水平距离不同降水深度的最终疏水沉降造成的井壁负摩阻力曲线.图5为同一降水深度不同水平距离的最终疏水沉降造成的井壁负摩阻力曲线.图6为同一深度同一水平距离处在不同疏水沉降时间处的井壁负摩阻力曲线.

3.2 井壁摩阻力分布规律

3.2.1 全负摩阻力现象

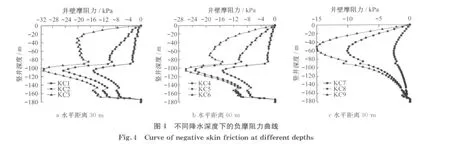
在桩土接触理论中，对负摩阻力沿深度的分布有以下认识［10］：桩越软弱土层进入相对较硬的土层，在软弱土层上部土的沉降量大于桩的沉降量，因而产生负摩阻力.而在软弱土层的下部因有较硬土层的承托，土的沉降量小于桩的沉降量，产生正摩阻力.在负摩阻力过渡为正摩阻力处，必然有一处摩阻力为零的地方，在该点桩身和土层的沉降量相等，该点即称为中性点.因此，负摩阻力呈现出折线变化.当土层特性出现较为复杂的软硬交替时，折线变化也会更加复杂，出现多中性点的情况.因理论上认为基岩不可压缩，所以当基岩作为持力层时，基覆岩交界处是中性点，即摩阻力为零.按照上述理论，因沉降产生的负摩阻力在桩身上将沿深度呈现出折线变化的趋势.但在图4—6中，可以看出竖井井壁上的摩阻力在整个深度范围内并未出现正负交替，亦即全负摩阻力，这与桩土接触有很大的不同.这是因为在计算中通过初始地应力平衡，假定竖井井壁受到含水层疏水沉降影响时已经基本完成了自重作用下的沉降，而且由于下端固结在基岩上，不可能发生二次沉降.尽管土体沉降会造成井壁竖向应变的产生，但混凝土的不易压缩性使其在整个界面上，该应变都要远小于土体的下沉量，造成整个井壁—土接触面上都会产生负摩阻力，这也与含水层疏水沉降理论相符合.

3.2.2 负摩阻力随深度变化规律

根据图4—6所示，可以看出井壁竖向负摩阻力的最大值发生于含水层与上层土体的交界处附近，位于第二土层内.此处与杨维好等［3－4］提出的“附加力沿深度呈非线性的递增关系，越靠近疏排水层与上覆土层的交界面附加力的值越大”并不一致.文献［4］中提出的弹性理论拟合公式中即假定竖向附加应力与深度呈正比关系，之后求解各系数皆基于此假设，但是此公式并未考虑基岩对沉降的影响.含水层疏水，造成水位下降，含水层的有效应力增大，产生固结压缩，引起上覆土体下沉，土体在沉降过程中施加于井壁外表面一个随着下沉而增加的竖向附加应力.而由于基岩的不可压缩性使得下层土体的沉降受阻，离下层土体较近的土层一方面在下层土体的带动下沉降，另一方面应力场的传递使其自身亦发生沉降，经沉降叠加效应而获得更大的沉降量；而距离较远的土层，在接受已经发生的沉降以及应力场的改变上存在滞后和衰减效应.在整个井壁—土体交界面上，最上层交界面处无论在水平距离上还是在竖直距离上离渗流点都最远，沉降量也最小.所以，负摩阻力在整个井壁上由上至下呈现出先增大，再减小的趋势，并在土层交界处（土层特性变化处）出现小范围内的不规律变化.

3.2.3 影响负摩阻力分布的因素

不同的降水深度反映了含水层疏水量的大小.理论上来说，对于同一水平距离的排水面，降水深度越深，渗流压力就越大，孔隙水压力消散得越快，土体产生的有效沉降也就越大.表现在井壁负摩阻力上，就会呈现出井壁负摩阻力在整体上随着降水深度的增加而增大，如图4所示.此规律与杨维好等［3－4］提出的“附加力与疏排水层的厚度成正比关系，疏排水层越厚，附加力越大”的结论是相一致的.

当排水面不低于含水层水位中线的情况下，水平距离30，60m处的排水面影响下的井壁摩阻应力曲线几乎重合.总体趋势上，负摩阻力受水平距离的影响并不如降水深度的剧烈.根据降水理论，如果给以足够长的时间，含水层水面最终会变为与排水面平行的极限状态.也就是如果排水面在同一高度，那么最终渗流情况也是相同的.这就决定了两者的沉降有可能会发生趋同，那么沉降引起的井壁负摩阻力也会具有这种特性.但这种趋同性并不适合于深降水，如图5c所示.深降水造成的地层扰动要大得多，而且其渗流曲线也会非常陡峻，这使得其降水不确定性更加显著，因此深降水在不同水平距离下造成的井壁负摩阻力也大不相同.值得注意的是，文中给出的降水深度为90m的情况，即将降水面设置在含水层底部，仅是一种理想化的最不利情况考虑，实际工程中是不可能达到如此低的渗透面.

另外，无论是水平距离的增加还是降水深度的增加，都会造成负摩阻力最大值往含水层移动的趋势.水平距离增加，意味着降水可以直接影响的上层土体离井壁的距离就越远，当这个距离超过一定范围时（本算例中大概在0.5倍井深的水平距离左右），其叠加位移效应的传递显然没有含水层通过水的渗流直接影响到含水层内的井壁—土体交界处来得快，因此最大的负摩阻力值就会下移至含水层内.同样的道理，当降水深度超过一定值后，在更大的水头压力下，水渗流速度加快，含水层疏水沉降速度也随之加快，在上层土体来不及发生叠加效应的时候，含水层土体已经再次沉降.这样，在相同的时间点上，含水层的沉降总是会超过上层土体的沉降，最终导致负摩阻力的峰值向含水层内移动.当渗流点水平距离为90m时，降水强度又较小，渗流沉降所产生的负摩阻力非常小，几乎可忽略不计.

随着降水时间的增加，孔隙水压力消散，土体会继续疏水沉降，土体的沉降量也会增加，负摩阻力也会随着土体沉降时间的增加而增加.另外，降水时间的增加会引起负摩阻力峰值向上层土体移动，这是因为下层土体的渗流最终会形成一个较稳定的渗流面，而上层土体的时间累积效应在逐渐发挥.此规律与杨维好等［3－4］提出的“负摩阻力随着沉降时间增长”相一致.

3.3 井壁负摩阻力限值

表4为各种情况下，在设定的渗流步长结束后，经计算得出的井壁摩阻力幅值和整个深度范围内均值的统计.

表4 负摩阻力幅值和均值统计表Tab.4 Amplitude and mean value of negative skin friction

当考虑最不利情况时，KC2，KC3，KC5，KC6均比较危险，若长时间抽水，KC9也有可能超过井壁摩阻力的最小限值.尽管在计算中已经考虑了200d的降水渗流，但是特殊地层条件下，该时间设置不足以完全考虑长期抽水的不利影响，特别是井壁摩阻力会随着渗流时间的增加而增大.当需要长期开采地下水，抽水位置不宜设置在竖井深度一半的范围内，且不宜进行深降水.如果无法避免，则应在靠近竖井方向设置隔断渗流的措施，防止在结构使用年限后期出现过大的竖向附加应力，同时应加强井壁变形监控，必要时应加强井壁构造.

4 结论

在竖井已经完成自重沉降以及材料线弹性的假设下，针对竖井井壁在沉降作用下的负摩阻力特性，给出以下结论：

（1）底部含水层疏水沉降引起的竖井井壁负摩阻力沿整个井土接触面分布，并呈现出 “两头小，中间大”的分布规律.

（2）在土层交界处，负摩阻力会表现出复杂的变化规律，可能会增大，也可能会减小.但总体上来说，土层特性影响土层负摩阻力的局部分布状况，在含水层确定的情况下，一般不会改变负井壁摩阻力的整体分布规律.

（3）一般来说负摩阻力值的大小受疏水面深度，即降水深度的影响要比受水平距离的影响大；无论是水平距离的增加还是降水深度的增加，都会造成负摩阻力最大值往含水层移动的趋势.

（4）负摩阻力峰值一般不在含水层内产生，而是在竖直方向上离疏水面最近的土层内产生.含水层深度一定时，只有当疏水面足够深时（大于含水层中水位线），或者疏水面离井土接触面足够远时，才有可能在含水层产生，且水平距离的影响大于降水深度.

（5）负摩阻力的大小随着降水时间的增加而增加.

［1］柏方俭.深冻结井井壁设计与施工的经验和教训［J］.建井技术，1996，17：27.BO Fangjian.Experiences and lessons for design and construction of shaft lining in deep overburden layer［J］.Shaft Construction Technology，1996，17：27.

［2］倪兴华.厚冲积层立井破裂机理与防治［M］.北京：煤炭工业出版社，2007.NI Xinghua.Fracture mechanism and prevention for shaft lining in deep Overburden layer［M］.Beijing：Coal Industry Press，2007.

［3］杨维好，崔广心，周国庆，等.特殊地层条件下井壁破裂机理与防治技术的研究（之一）［J］.中国矿业大学学报，1996，25（4）：1.YANG Weihao，CUI Guangxin，ZHOU Guoqing，et al.Fracture mechanism and prevention for Shaft Lining in special layer（I）［J］.Journal of China University of Mining and Technology，1996，25（4）：1.

［4］崔广心，杨维好，吕恒林.深厚覆盖层中的冻结壁和井壁［M］.徐州：中国矿业大学出版社，1998.CUI Guangxin，YANG Weihao，LV henglin.Frozen shaft lining in overburden layer.［M］.Xuzhou：China Mineral University Press，1998.

［5］聂如松，冷伍明，杨奇，等.桩—土间剪切应力的传递探讨［J］.岩土力学，2009，30（3）：799.NIE Rusong，LENG Wuming，YANG Qi，et al.Discussion on shear stress transfer between pile and soil［J］.Rock and Soil Mechanics，2009，30（3）：799.

［6］严驰，冯海涛，李亚坡.深基坑开挖中坑内降承压水的有限元模拟分析［J］.西安石油大学学报，2007，22（2）：29.YAN Chi，FENG Haitao，LI Yapo.Analysis of the deformation and stability of a deep foundation pit in the pumping process of the confined water inside it through finite element simulation［J］.Journal of Xi’an Shiyou University，2007，22（2）：29.

［7］袁灯平，黄宏伟，马金荣.软土地基桩侧表面负摩阻力解析模型［J］.上海交通大学学报，2005，39（5）：731.YUAN Dengping， HUANG Hongwei， MA Jinrong. An analytical model of negative skin friction of piles in soft soil［J］.Journal of Shanghai Jiaotong University，2007，22（2）：29.

［8］曹洪，罗彦，周红星.新光大桥桥墩钢板桩围堰抗渗问题分析［J］.岩石力学与工程学报，2006，25（1）：152.CAO Hong， LUO Yan， ZHOU Hongxing. Analysis of permeability of cofferdam with armor－plate pile for Xinguang Bridge’s pier［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25（01）：152.

［9］Crawford R J，Byfield M P.A numerical model for predicting the bending strength of Larssen steel sheet piles［J］.Journal of Constructional Steel Research，2002，58：1361.

［10］Charles I，Mansur P E.Dewatering cofferdam for construction of Olmsted Locks［J］.Journal of Geotechnical Engineering，2002，128（6）：496.