平面K型圆管节点新的承载力计算公式

童乐为，孙建东，2，陈以一

（1.同济大学 建筑工程系，上海 200092；2.山东省建筑科学研究院，山东 济南 250031）

钢管桁架已在国内外结构工程中得到广泛的应用.在直接焊接的相贯节点研究中，对平面K型圆钢管节点（见图1）极限承载力的研究成果最为丰富［1－10］.这些研究成果反映在了各国钢结构设计规范（指南、手册）中，对于平面K型圆钢管节点来说，其承载力计算公式主要来源有我国钢结构设计规范（GB 50017—2003）［11］、欧洲规范（Eurocode 3）［12］、美国焊接学会规程（AWS）［13］、日本建筑学会规范（AIJ）［14］、陈誉公式［1］和 M.M.K.Lee公式［2］.

尽管规范对已有研究成果进行了归纳和总结，但并非所有问题都已得到完满解决，目前规范或研究中尚存在如下不足或未考虑的影响因素：① 在有限元分析上，文献［3－4］对K型圆钢管搭接节点的极限承载力进行了数值分析，但尚未考虑内隐蔽部分焊接与否以及腹杆搭接顺序等施工因素对节点受力性能和极限承载力的影响；文献［2，5－6］考虑了上述施工因素，但其研究主要基于数值分析，没有试验研究的支持；② 在公式形式上，M.M.K.Lee公式仅针对平面K型搭接节点承载力的计算，不能应用于间隙节点；我国规范公式主要建立在间隙节点基础上，对搭接节点按间隙为零考虑，整体上偏于保守，陈誉公式对此做了修正，提出了平面K型搭接节点的计算公式，但由此得到的平面K型节点承载力计算公式有两个，未统一公式形式，而Eurocode 3，AIJ均用一个统一的公式来计算平面K型间隙和搭接节点，更加简洁合理；③ 在承载力研究上，影响搭接节点承载力的诸多因素（如搭接顺序、内隐蔽部分焊接与否等）在现有各规范公式中尚未得到反映.已有的有限元分析［2，5］表明：腹杆搭接顺序和内隐蔽部分是否焊接，节点承载力最大可相差30%；文献［12］的试验研究也表明，上述两因素将影响节点的内力传递路线和破坏模式.因此，在节点承载力计算公式中反映上述影响因素是非常必要的.

图1 平面K型圆钢管节点Fig.1 Uniplanar CHS K－joint

本文的研究综合考虑了上述平面K型圆管节点承载力的诸多影响因素，建立了有限元分析模型并经过了试验验证；在此基础上，对4类K型节点型式（① 平面K型间隙节点，K－Gap型；② 贯通腹杆受压且内隐蔽部分焊接的平面K型搭接节点，K－CW型；③ 贯通腹杆受拉且内隐蔽部分焊接的平面K型搭接节点，K－TW 型；④ 贯通腹杆受拉且内隐蔽部分不焊接的平面K型搭接节点，K－TN型）进行了非线性有限元计算，建立了极限承载力结果数据库；以此为依据通过多元非线性回归，提出了可进行平面K型间隙和搭接节点承载力计算的统一公式；进而与国际管节点数据库中试验数据以及与现有规范公式进行了纵横向比较，验证本文提出的公式具有较高精度和安全可靠性.

1 有限元分析模型及其试验验证

1.1 有限元分析模型

本文有限元分析采用ANSYS软件库中的SHELL 181壳单元进行建模和计算.非线性分析求解时采用弧长法，在出现负刚度时即终止分析.

1.1.1 边界条件和加载方式

边界条件如图2所示.弦杆一端按完全固定支座考虑，另外一端为仅有沿杆轴线方向位移的固定支座.两腹杆端部边界为滑动铰支座，仅允许沿杆轴线方向有位移，约束径向位移.在有限元模型中为了方便控制杆件端部的约束类型，在节点模型划分网格以后，各杆件端部的约束以节点约束的形式施加在端部截面中所有的节点上，并编程实现杆件端部约束的可控变换，增强施加有限元约束类型程序段的适应性；同时考虑到平面K型节点的对称性，为减少有限元模型的计算成本和提高计算效率，有限元模型取1／2结构并施加对称约束.腹杆和弦杆的长度均从两相交杆件的根部开始外伸4倍的管直径，以消除端部加载条件对节点区域的影响.施加腹杆轴向荷载（图2中Nc，Nt分别表示施加在腹杆端部的轴压力和轴拉力）时，仅在两腹杆末端节点上沿腹杆轴向均匀施加反对称的集中面荷载.

图2 平面K型节点的边界条件和加载方式Fig.2 Boundary and loading conditions of uniplanar K－joint

1.1.2 焊缝模拟

有限元分析模型中考虑了实际焊缝的存在，对节点的连接焊缝进行了模拟.建立了壳体角焊缝模型［1］，焊缝强度同母材.焊缝模型中不计残余应力的影响.

1.1.3 内隐藏部分焊接与否的模拟

建模时依据贯通腹杆与弦杆之间内隐藏焊缝焊接与否，分别建立不同的壳体角焊缝模型，并采用不同的网格划分方案：未焊接时，腹杆和弦杆的相邻单元不共点；否则，两者间的单元共点相合，见图3.

图3 内隐蔽部分焊接与否的模拟Fig.3 Simulation of hidden weld absence／presence

1.1.4 材料性能

节点材料采用双线性模型，弹性模量、切线模量以及屈服强度采用材性试验数据，泊松比υ取为0.3.有限元计算中节点的外荷载未考虑自重影响.材料弹塑性的发展和单元刚度由Von－Mises屈服准则及相关的流动法则确定，并采用等向强化理论.

1.2 极限承载力判别准则

以杆件承受轴力为主的圆管相贯节点，其极限承载力主要有如下3种判别准则：① 将腹杆轴力和对应于腹杆轴线方向的腹杆与弦杆管壁相对变形作为荷载—位移曲线，以该曲线的极值点作为极限承载力，称为极限强度准则；② 弦杆管壁沿腹杆方向变形达到某一限值，称为极限变形准则，本文以国际上通用的弦杆管壁沿腹杆方向变形为3%D时对应的荷载为依据；③ 受拉腹杆表面或杆件交汇处的应变达到20%ε（ε为材料极限拉应变）.虽然本文有限元计算不能模拟节点断裂现象，但通过此方法可以近似认为节点已产生受拉初裂缝，称为断裂准则.

节点极限承载力取为按上述3种准则确定的各杆所受轴力中的较小值.

1.3 国际管节点数据库试验验证

国际管节点数据库［7］提供了大量的平面K型圆管节点试验数据，本文从中选取了38个试验节点（其中包括22个间隙节点和16个搭接节点），对上述初步建立的有限元分析模型进行极限承载力校验，借以广泛验证模型的适用性.

结果表明，有69%的节点计算值与试验值的相对误差绝对值都在10%以内，相对误差绝对值大于20%的节点不足5%.可见，本文建立的有限元分析模型可以较为准确地得到实际节点的极限承载力，可作为后续平面K型圆管节点极限承载力计算的基础.

1.4 计算参数

考虑到节点的几何参数比较多，在几何参数变化时，为使节点腹杆轴力偏心均在规范规定的范围以内，本文在选取节点模型几何参数时，弦杆的直径D均取为200mm，腹杆与弦杆夹角θ1和θ2的取值，对于K－Gap型节点，均取为45°，变化的量纲一几何参数主要包括管径比β、径厚比γ、管厚比τ和两腹杆间隙与管径比ζd；而对于 K－CW 型、K－TW 型、KTN型节点，腹杆与弦杆夹角θt和θc均取为60°，变化的量纲一几何参数主要包括β，γ，τ和搭接率Ov.

为全面剖析各几何参数对极限承载力的影响，采用全面分析法，各几何参数均取3个水平，取值如表1所示.

本文对每一类型的K型节点，均进行了几何参数组合下的极限承载力非线性计算，共得到4×81＝324个节点的有限元数据，以此为基础进行平面K型节点承载力公式回归.

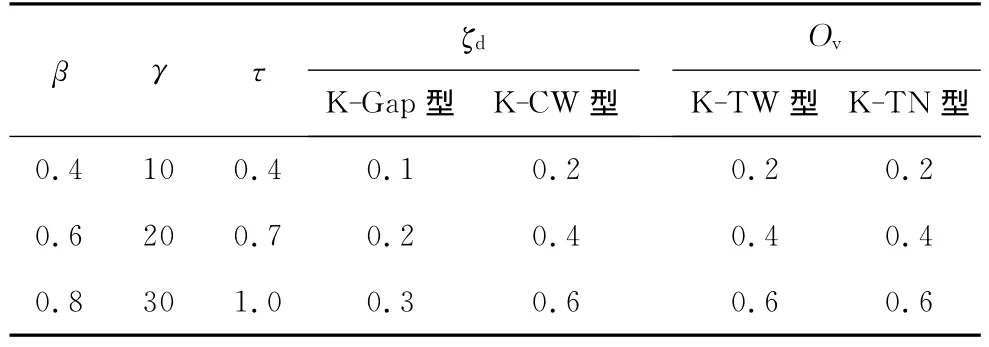
表1 节点几何量纲一参数一览表Tab.1 Geometric parameters of CHS K－joint

2 节点极限承载力回归公式

2.1 公式形式及回归

纵观现有文献，以弦杆管壁塑性破坏模式为主的节点承载力计算公式其回归形式可归纳为如下3种：

（1）在Togo提出的环模型［15］基础上进行回归，公式为

式中：Pu′K为K型节点极限承载力；Qu为量纲一几何参数的函数，函数表达式为 Qu＝Q（β，γ，τ，n，...）；其余未特别说明的符号意义同我国《钢结构设计规范》（GB 50017—2003）［11］，下同；

（2）在某一公式基础上进行修正，以提高精度，例如陈誉公式［1］；

（3）设定公式形式直接进行回归，如 M.M.K.Lee公式［2］.

现行国内外规范中钢管节点承载力公式大多采用第（1）种形式.考虑与原有规范公式形式的衔接和统一，本文公式采用如下回归形式：

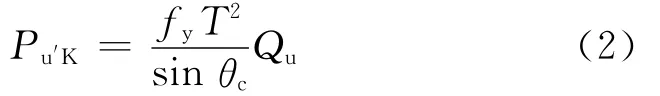
其中Qu考虑不同参数类型对承载力的影响，可将其分离变量为

式中：Qg为几何系数，为几何量纲一参数的函数，本文设定其函数形式为

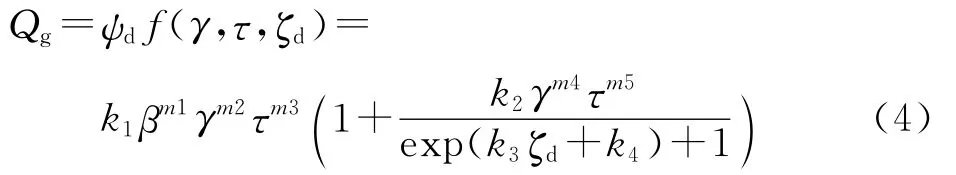
Qld为由搭接顺序和内隐藏焊缝是否焊接等因素决定的系数，本文在K－CW型节点承载力基础上回归K－TW型和K－TN型节点，设定其形式为ψn为弦杆附加轴力系数，函数表达及意义同我国《钢结构设计规范》（GB 50017—2003）［11］.

式（4），（5）中：k1—k5，m1—m9均为待定回归参数.

式（2）为一非线性函数，待求参数共19个，可利用计算的K型节点承载力有限元结果数据，通过多元回归技术得到各待定回归参数的最佳估算值.为便于工程应用，对回归参数进行微调，最终得到各待定参数如表2和表3所示.

表2 式（4）中回归系数取值Tab.2 Value of regression coefficient in Equation（4）

表3 式（5）中回归系数取值Tab.3 Value of regression coefficient in Equation（5）

综上所述，K型节点极限承载力计算公式的最终表达式为

2.2 极限承载力回归公式与试验结果比较

文献［8］对内隐蔽部分焊接与否以及腹杆搭接顺序等施工因素影响下的K型搭接节点进行了试验研究.本文回归的式（6）计算值与相应的试验节点的极限承载力值的比较分析见表4.

公式计算中用到的杆件截面尺寸、材料强度均采用试验实测值.可见，式（6）的计算值与试验值较为接近，这说明本文回归的极限承载力计算公式可以较为准确地预测平面K型节点极限承载力.

2.3 几何参数ζl与f（γ，τ，ζd）的关系

图4显示了平面K型节点承载力回归公式中函数f（γ，τ，ζd）随几何参数ζl，γ变化的情况.图中纵坐标为f（γ，τ，ζd）；横坐标为ζl，ζl＝g1／T，反映了两腹杆之间的相对间隙，ζl为正值表示间隙节点，ζl为负值表示搭接节点.

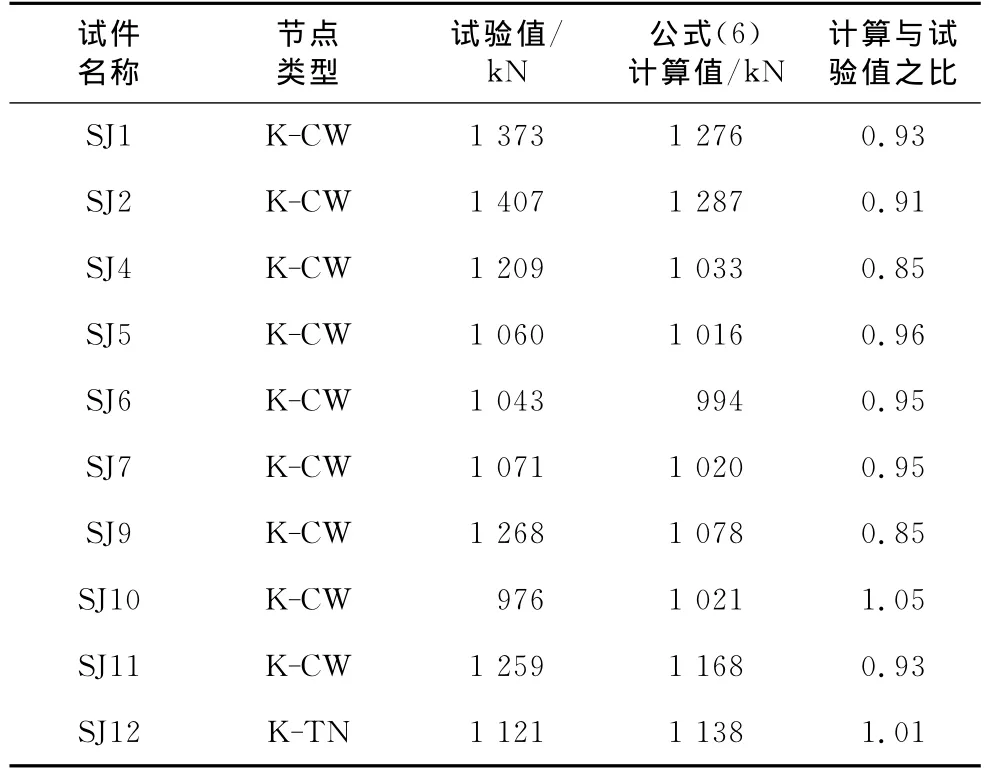
表4 节点极限承载力公式计算值与试验值的比较Tab.4 Comparison between formula and test

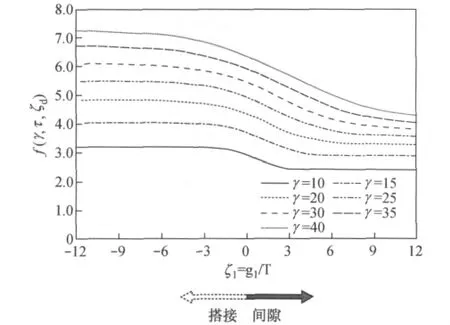
图4 f（γ，τ，ζd）—ζl 曲线（τ＝0.7）Fig.4 f（γ，τ，ζd）andζlcurves（τ＝0.7）

图4中显示的曲线具有如下特点：① 无论K型间隙节点还是搭接节点，两腹杆之间的间隙越小，对极限承载力的影响越明显；在γ，τ一定，ζl超出某一值时，两腹杆间隙对极限承载力基本无影响；② 本文回归的K型节点极限承载力计算公式（6）由间隙型过渡到搭接型是连续的，呈现逐渐增大的趋势，中间无突变.这说明本文回归公式（6）可以实现用统一的公式形式来计算K型间隙和搭接节点.

3 节点承载力设计值建议公式

式（6）拟合的曲线是保证率50%的均值线，用于设计偏于不安全，若要进行工程应用，需要换算为节点承载力设计值的计算公式.

节点承载力设计值计算公式是由节点极限承载力计算公式按设计要求换算得到的，原则上应按照我国《建筑结构设计统一标准》，考虑结构构件抗力的主要不定性因素（包括材料性能的不定性、几何参数的不定性，以及计算模式的不定性）并进行可靠性分析得到.我国《钢结构设计规范》（GB 50017—2003）实际上是采用实用的安全系数换算方法将平面K型节点极限承载力计算公式换算为节点承载力设计值公式的.文献［16］给出了该安全系数换算方法.

本文采用该方法，最终得到的平面K型节点承载力设计值建议公式的表达形式如下：

（1）受压腹杆在管节点处的承载力设计值建议公式为

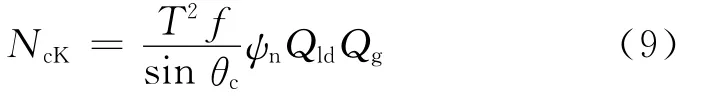
式中，Qg为几何系数，计算式为

f为弦杆的抗拉强度设计值；其余符号意义同式（6）.

（2）受拉腹杆在管节点处的承载力设计值建议公式为

需要说明的是，本文建议公式是在平面K型节点可能的几何参数范围内回归得到的.因此，本文建议公式的适用范围如下：0.2≤β≤1.0；γ≤35；0.2≤τ≤1.0；20% ≤Ov≤100%；di／2ti≤30；30°≤θ≤90°.

4 建议公式与试验数据的比较

待比较的试验数据来自于Makino钢管节点试验数据库［7］，为避免试件尺寸效应的影响，去除小直径节点，共选取350个节点数据（其中包括259个间隙节点和91个搭接节点）.将试验节点参数的有关数据代入式（9），所得计算值与试验值比值的统计结果如图5所示.图中，节点类型为间隙节点和搭接节点，节点数量350，比值的最大值1.5430，最小值0.5485，平均值0.8405，标准差0.1322，离散度0.1573.

从图5可以看出，本文建议公式计算值与试验值的比值有89.4%的数据点集中在［0.6，1.0］范围内，平均值为0.8405，与试验值的误差较小且建议公式值大多在试验值以下.这说明本文建议公式预测精度较好且安全可靠，可以用于工程设计.

图5 建议公式值Nck与数据库试验值Nu′k的比值统计直方图Fig.5 Histogram of ratio of recommended formula to test results

5 建议公式与现有规范公式的比较

为横向比较本文建议公式与现有规范公式，将国际管节点数据库［7］中的试验数据分为平面K型间隙节点和搭接节点分别予以比较.

5.1 K－Gap型节点

试验数据来自于国际管节点试验数据库，去除小直径节点，共选取259个间隙节点.将试验节点的实际几何参数、实测材料强度代入本文建议公式和现有各规范公式，得到各公式计算值与试验值比值的统计参数比较如表5所示.

由表5比较可知，本文建议公式相比较现有我国《钢结构设计规范》（GB 50017—2003），平均值从0.7987提高到0.8353，同时建议公式的标准差和离散度均较小；与欧洲规范Eurocode 3相比，在离散度相等的情况下，建议公式平均值明显较高；建议公式各统计指标与日本建筑学会AIJ公式较为接近.

5.2 K－CW 型节点

试验数据来自于国际管节点试验数据库［7］，共选取91个搭接节点.各公式计算值与试验值比值的统计参数比较如表6所示.

从表6统计比较中可以看出，对于K－CW型节点，本文建议公式相比较陈誉公式和日本建筑学会AIJ公式，在平均值较为接近的情况下，本文建议公式的标准差和离散度均明显较小，且本文公式计算值与试验值的比值大于1的个数明显少于陈誉公式和AIJ公式，这说明本文公式精度较好且更为安全可靠；与欧洲规范Eurocode 3和美国焊接学会AWS公式相比，本文公式精度较高且离散度小.

表5 建议公式与现有规范公式基于试验节点K－Gap的比较Tab.5 Ratio of recommended formula and existing codes to test results of K－Gap

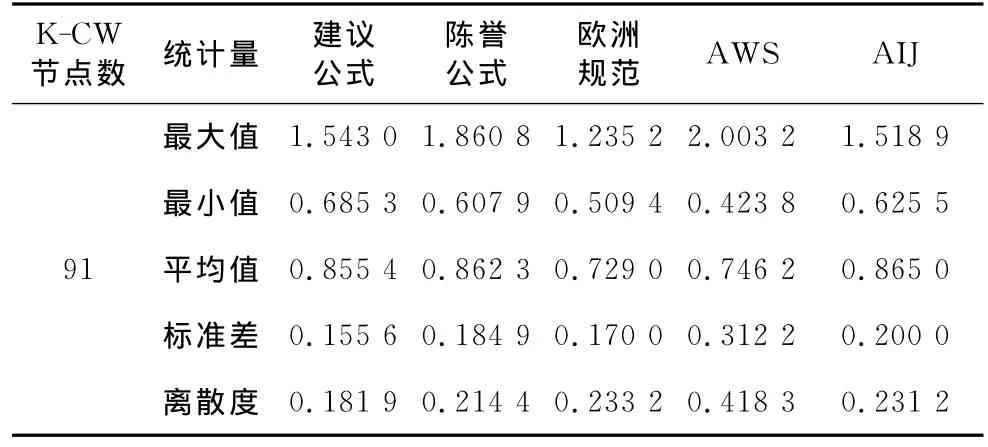
表6 建议公式与现有规范公式基于试验节点K－CW的比较Tab.6 Ratio of recommended formula and existing codes to test results of K－CW

6 结论

（1）本文建立的平面K型节点有限元分析模型考虑了搭接顺序和内隐蔽部分焊接与否等施工因素的影响，并结合试验数据进行校准研究，适应性良好，可以做为参数分析和节点极限承载力计算的基础.在此基础上，建立了平面K－Gap型、K－CW型、K－TW型和K－TN型节点的极限承载力有限元数据库.

（2）通过多元非线性回归提出了统一的平面K型节点的极限承载力计算公式，进而提出了承载力设计值建议公式，并与国际管节点数据库中试验数据以及与现有规范公式进行了比较评价，证明本文回归的公式具有较高精度和更为广泛的适用性，具有以下特点：

①形式统一，相对于中国《钢结构设计规范》（GB 50017—2003）中平面K型节点公式和陈誉公式来说，本文提出的承载力建议公式可用于平面K型间隙和搭接节点的承载力计算，形式上统一，且由间隙型过渡到搭接型，连续性好、中间无突变；

②公式全面，相对于欧洲规范Eurocode 3，AIJ，AWS等公式来说，本文公式综合考虑了搭接顺序和内隐蔽部分焊接与否等因素对承载力的影响，从而使影响承载力的诸多因素在公式中得到了全面反映；

③ 结果精确，通过与国际管节点数据库中试验数据的纵横向比较，证明本文建议公式对于平面K型节点承载力计算是较为准确的；

④ 安全可靠，由极限承载力计算公式转化为设计承载力公式，考虑了中国《钢结构设计规范》（GB 50017—2003）所采用的安全系数换算方法，且通过与试验节点的统计比较表明本文回归的承载力建议公式是安全可靠的.

［1］陈誉.平面K型圆钢管搭接节点静力性能研究［D］.上海：同济大学建筑工程系，2006.CHEN Yu.Research on static behaviour of unstiffened overlapped circular hollow section K－joints［D］.Shanghai：Tongji University.College of Civil Engineering，2006.

［2］Dexter E M，Lee M M K.Static strength of axially loaded tubular K－joints II ：ultimate capacity ［J］.Journal of Structural Engineering：ASCE，1999，125（2）：202.

［3］舒兴平，朱邵宁，朱正荣.K型圆钢管搭接节点极限承载力研究［J］.建筑结构学报，2004，25（5）：71.SHU Xingping，ZHU Shaoning，ZHU Zhengrong.The study of ultimate bearing capacity of overlapped CHS K－joints［J］.Journal of Building Structures，2004，25（5）：71.

［4］罗尧治，张楠.K型搭接节点承载力性能分析及建议公式［J］.钢结构，2004，19（3）：23.LUO Yaozhi，ZHANG Nan.Ultimate bearing capacity analysis and proposal of formula for lapped tubular K－joints［J］.Steel Construction，2004，19（3）：23.

［5］Dexter E M，Lee M M K.Static strength of axially loaded tubular K－joints I：behavior ［J］.Journal of StructuralEngineering：ASCE，1999，125（2）：194.

［6］Gazzola F，Lee M M K，Dexter E M.Design equation for overlap tubular K－joints under axial loading ［J］.Journal of Structures Engineering：ASCE，2000，126（7）：798.

［7］Makino Y，Kurobane Y，Ochi K，et al.Database of test and numerical analysis results for unstiffened tubular joints［R］.［S.l.］：IIW，1996.

［8］赵宪忠，陈誉，陈以一，等.平面K型圆钢管搭接节点静力性能的试验研究［J］.建筑结构学报，2006，27（4）：23.ZHAO Xianzhong，CHEN Yu，CHEN Yiyi，et al.Experimental study on static behavior of unstiffened，overlapped CHS K－joints［J］.Journal of Building Structures，2006，27（4）：23.

［9］Wardenier J，Kurobane Y，Packer J A，et al.Design guide for circular hollow section（CHS）joints under predominantly static loading［M］.［S.l.］：TUV Rheinland verlag Gm6H，2008.

［10］International Institute of Welding.Static design procedure for welded hollow section joints—recommendations［S］.Singapore：IIW，2009.

［11］中华人民共和国建设部.GB 50017—2003钢结构设计规范［S］.北京：中国计划出版社，2003.Ministry of Construction of the People’s Republic of China.GB50017—2003 Code for design of steel structures［S］.Beijing：China Planning Press，2003.

［12］European Committee for Standardisation（CEN）.Design of steel structures，Part 1－8：design of joints ［S］.Brussels：European Committee for Standardisation（CEN），2005.

［13］American Welding Society.ANSI／AWS D1.1－2000 Structural welding code—steel［S］. ［S.l.］： American Welding Society，2000.

［14］Architectural Institute of Japan.Recommendations for the design and fabrication of tubular truss structures in steel［S］.Tokyo：Architectural Institute of Japan，2002.

［15］Togo T.Experimental study on mechanical behaviour of tubular joints［D］.Osaka：Osaka University，1967.

［16］钢结构设计规范编制组.中华人民共和国国家标准《钢结构设计规范》应用讲解［M］.北京：中国计划出版社，2003.The Compilation Group of Code for Design of Steel Structures.Application and explaination of code for design of steel structures［M］.Beijing：China Planning Press，2003.