光刻投影物镜光学元件运动学支撑结构的设计与分析

倪明阳 ，巩 岩

(中国科学院 长春光学精密机械与物理研究所 应用光学国家重点实验室，吉林 长春130033)

1 引 言

随着半导体工业对深紫外光刻投影物镜分辨率的要求不断提高，深紫外光刻投影物镜的数值孔径和光学元件口径越来越大，使光学系统对支撑结构的机械加工精度、外界应力及环境变化的影响愈加敏感［1-2］。193 nm 深紫外光源长时间曝光累积的热量引起的物镜内光学元件温度变化以及外界应力的传入都会影响光学元件表面面形，导致光刻机成像质量下降，使其无法达到应有的分辨率。深紫外光刻投影物镜光学元件的支撑结构不仅仅要满足定位精度的要求，还应能够补偿外界应力、温度变化等因素对像差造成的不良影响。传统的高精度光学元件采用胶粘支撑方式，温度变化时，胶点本身的弹性在一定程度上可以减轻光学元件和镜框材料线膨胀系数不匹配导致的差分膨胀，但是，由于胶点厚度的限制，这种补偿效果有限，并且胶粘支撑方式无法消除外界应变的影响。因而，传统的支撑方式已经难以满足高精度光刻投影物镜对光学元件面形精度的要求［3］。

2010 年，国内提出一种用于空间光学遥感器反射镜的柔性支撑结构［5］，该结构采用在镜框内壁加工出径向柔性弹片的方式，能够对温度变形做一定的补偿，在力-热耦合状态下反射镜面形的PV 值为59.03 nm，RMS 值为9.11 nm。提出的另一种无隙支撑方式可应用在空间光学遥感器的次镜上［6］，解决了温度变化范围较大时各胶点热应力对面形影响的不可逆问题，反射镜镜面面形小于0.02λ。这两种柔性支撑方式能够有效地补偿温度对面形的影响，但是加工误差或装调力对面形的影响无法消除。对于光学元件口径为200 ～300 mm 的光学元件，机械支撑结构的加工精度可达到几十微米，在固定光学元件时，由于加工误差或装调力产生的外界应变对面形的影响不可忽略。

本文提出了一种深紫外光刻投影物镜光学元件运动学支撑结构，研究了支撑结构中支座的径向柔度特性，分析了外界温度变化和应变对光学元件表面面形精度的影响。同三点胶粘支撑方式的分析结果对比表明，该支撑结构能够有效消除外界温度变化对光学元件面形的影响，并可显著消除由装配应力或者加工制造误差造成的外界应变对光学元件面形精度的影响。

2 光学元件设计要求

针对用于深紫外光刻投影物镜中的典型双凸透镜进行支撑结构的研究，该透镜的形状和结构如图1 所示。其典型特点是:通光孔径较大;定位精度和面形精度要求远高于常规物镜。对透镜径向和轴向位置精度的要求在亚微米级，对上下表面面形精度的RMS 值要求小于1 nm。

图1 光学元件结构尺寸参数Fig.1 Parameters of lens

影响光学元件面形精度的主要因素有自重变形、紧固力、热载荷、外界应力等。在光学元件的加工和检测过程中，可有效去除光学元件自重和紧固力对元件面形的影响，因而在设计和分析中主要考虑工作阶段的热载荷和外界应力对光学元件面形精度稳定性的影响。

3 支撑结构及其径向柔度设计

3.1 支撑机构原理

光学元件支撑组件包括: 光学元件、镜框、支座，如图2 所示。透镜通过3 个支座固定在镜框上，镜框和支座的材料均采用不锈钢。

图2 光学元件支撑结构Fig.2 Construction of lens mounting

支座结构包括支撑台、球铰、连杆、转铰和底座，如图3 所示。光学元件固定在支撑台上，底座通过螺钉连接在镜框上。支座底部转铰为单轴柔性铰链，支座顶端球铰采用直圆型双轴柔性铰链。

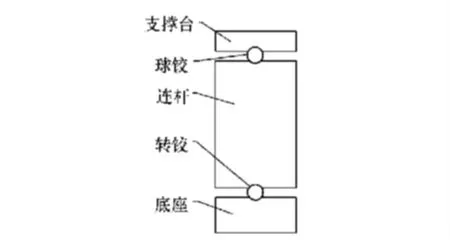
图3 支座结构Fig.3 Structure of supporting seat

整个光学元件支撑结构的原理如图4 所示，连接光学元件的3 个球铰可等效为具有3 个旋转方向柔度的弹簧，与镜框较近的3 个转铰可视为仅有一个旋转方向柔度的弹簧。柔性球铰和柔性转铰通过串联的方式构成单个支座，3 个支座以并联的方式支撑光学元件。

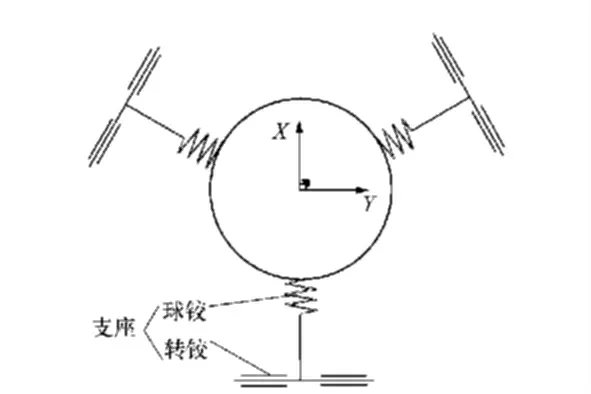
图4 光学元件支撑方式原理Fig.4 Scheme of lens supporting method

球铰具有3 个方向的转动自由度，作用在光学元件与支撑台连接的局部区域，使光学元件与支撑台实现最大程度的贴合; 转铰只有一个方向的转动自由度，使得光学元件具有径向的自由度。球铰和转铰组合的结构使单个支座限制了光学元件沿其边缘圆周方向移动的自由度和沿光轴方向移动的自由度，释放了其他自由度。3 个支座并联共同支撑光学元件时，可对光学元件空间六个自由度完全约束而不产生过约束，实现了光学元件支撑方式的近似静定结构。

当温度变化时，支座的径向柔度允许光学元件自由膨胀或收缩，不会导致光学元件表面面形过度劣化，从而抵消热载荷的影响。外界应变传入镜框会导致3 处支撑台不在同一平面上，柔性球铰本身的顺应性会消除平面度公差对光学元件产生的弯矩，从而减小光学表面面形精度的劣化，实现光学元件的极小应力支撑［7-10］。

3.2 支座径向柔度设计

补偿热应力的主要因素是支座沿光学元件径向方向上的柔度，所以对支座柔度特性的分析主要考虑对支撑性能影响最关键的径向柔度。

支座受力如图5 所示，O点为支座总体坐标系O-XO-YO的坐标原点，Y轴指向光学元件的半径方向，X轴方向与光学元件的光轴一致。FOY为作用在支座原点O处的Y向力。为了求得整个支座的径向(Y向) 柔度，在现有的单轴柔性铰链［11］和双轴柔性铰链［12］理论公式基础上，分别求得两者相对于支座总体坐标系的柔度，再把两者叠加。

通过支座中支撑台和连杆的放大作用，将径向力FOY作用下单轴柔性铰链的末端位移转化到O点上，柔性铰链的柔度即可转换为支撑点O处的柔度。在总体坐标系下，单轴柔性铰链单独作用时支座的径向柔度为:

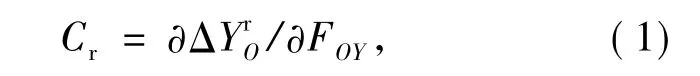
式中，ΔYrO为单轴柔性铰链单独作用时径向力FOY作用下O点沿Y向的位移量。

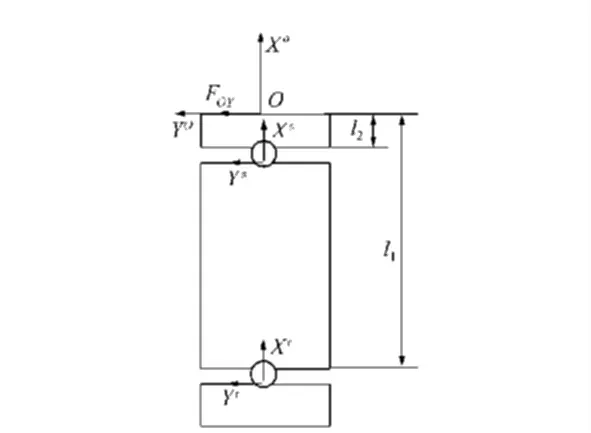
图5 单轴柔性铰链对支座的柔度Fig.5 Compliance of supporting seat with single-axis flexure hinge

通过支座中支撑台的放大作用，将径向力FOY作用下双轴柔性铰链的末端位移转化到O点，双轴柔性铰链的径向柔度即可转换为支撑点O处的柔度。在总体坐标系下，双轴柔性铰链单独作用时支座的径向柔度为:

式中，ΔYsO为双轴柔性铰链单独作用时径向力FOY作用下O点沿Y向的位移量。

由于单轴柔性铰链和双轴柔性铰链在单个支座上是串联的，所以整个支座的径向柔度为两铰链在总体坐标系下径向柔度之和:

式中，C为支座整体的径向柔度。

为了对支座的径向柔度进行验证，设置相同的结构参数，采用支座整体径向柔度推导公式计算不同径向力作用下O点的Y方向位移，并与有限元分析结果对比。得到支座O点的Y方向位移结果如表1 所示。

支座的径向柔度为12.243 ×10-4mm/N，理论计算值和仿真分析值误差绝对值在2.2% 以内，两者非常一致。由于在理论计算中将连杆、支撑台、底座均作为刚体考虑，而有限元仿真分析中则包含了连杆、支撑台、底座的变形;另外，有限元分析时边界条件的定义具有一定程度的近似性，这是导致两者计算结果有差异的主要因素。

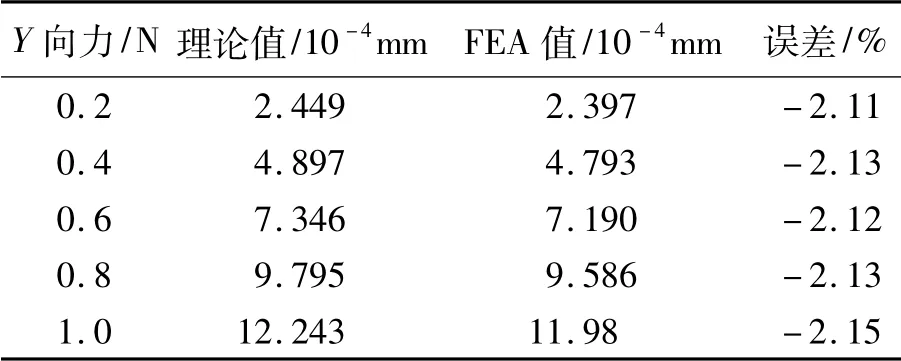
表1 支座O 点Y 轴位移理论值和仿真值对比Tab．1 Comparison of Y translations of point O between theoretical formula and FEA simulation

4 支撑结构性能分析

通过解析法直接计算热载荷和外界应变对任意光学元件面形精度的影响十分困难，因而采用数值模拟的方法分析光学元件上下表面面形在支座支撑下的变化情况。

在NX/NASTRAN 中建立光学元件及支撑机构的仿真模型，对支撑机构的消热、消应变性能进行分析，考察温度变化、外界应变对光学元件上下表面面形的影响。鉴于所分析对象的小变形特性，在计算前进行了有限元网格的独立性验证:逐步减小网格划分的尺寸，使两次计算结果差值小于0.01%。消除网格精度对计算结果影响后，光学元件及其运动学支撑结构的有限元模型如图6所示。

图6 支撑结构有限元模型Fig.6 FEA model of supporting structure

有限元模型的设置如表2 所示。材料属性如表3 所示。

表2 仿真模型设置Tab．2 Setting of FEA model

表3 材料属性Tab．3 Properties of different materials

4.1 温度变化对面形的影响

在光刻投影物镜的装配、运输过程中温度变化范围较大，容易对光学元件定位产生偏心误差，温度变化剧烈时，甚至会使光学元件破裂。但是在工作过程中，由于微环镜控制系统的作用，光刻投影物镜内部温度变化范围较小。这里对有限元模型施加一个整体的温度变化，提取上下表面节点的位移信息进行曲面拟合，求出了上下表面面形的PV 值和RMS 值的变化情况。

上下表面的变形如图7 和图8 所示，在光学元件的3 个支撑点附近由于热应力的影响，面形变化梯度较大，中心区域变形较为平缓。

图7 温度升高0.1 ℃时光学元件上表面变形Fig.7 Top surface deformation with 0.1 ℃temperature rise

图8 温度升高0.1 ℃时光学元件下表面变形Fig.8 Bottom surface deformation with 0.1 ℃temperature rise

由图9 和图10 可以看出，温度变化时光学元件上下表面变形的方向相反。温度升高0.1 ℃时上表面面形的PV 值为2.68 nm，RMS 值为0.348 nm;下表面面形的PV 值为2.53 nm，RMS值为0.357 nm。

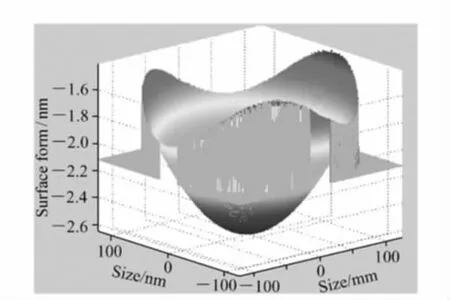
图9 温度升高0.1 ℃时光学元件上表面面形Fig.9 Top surface form with 0.1 ℃temperature rise

图10 温度升高0.1 ℃时光学元件下表面面形Fig.10 Bottom surface form with 0.1 ℃temperature rise

为了验证运动学支撑方式的性能，把温度变化从0.1 ℃升高到0.5 ℃，比较了运动学支撑与传统三点胶粘支撑方式下的面形变化。为保证两种支撑结构在形式上的近似性，胶点也分布在光学元件下表面的底部，其径向位置与运动学支撑方式中支座相同，胶点厚度为0.5 mm，直径为5 mm。光学元件面形变化的PV 值对比如图11所示，面形变化与温度基本呈线性关系。采用支座支撑的光学元件上表面面形PV 值约为三点胶粘支撑时的1/5，采用支座支撑的光学元件下表面面形PV 值小于三点胶粘支撑的1/9。

图11 温度升高0.5 ℃时与三点胶粘支撑面形PV值比较Fig.11 Comparison of PV values with 0.5 ℃temperature rise by kinematic supporting structure and 3-point glue supporting structure

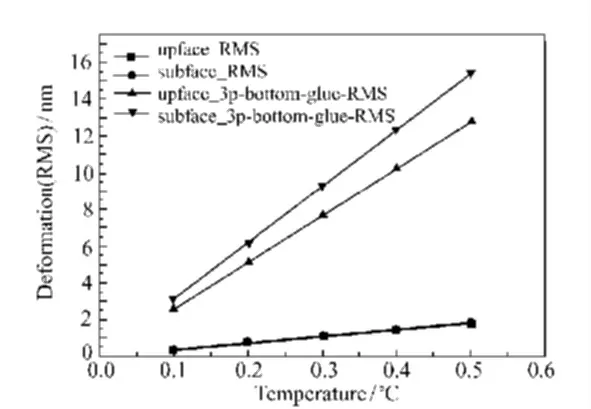
图12 温度升高0.5 ℃时与三点胶粘支撑面形RMS值比较Fig.12 Comparison of RMS values with 0.5 ℃temperature rise by kinematic supporting structure and 3-point glue supporting structure

光学元件面形变化的RMS 值对比如图12 所示。采用支座支撑的光学元件上表面面形RMS值小于三点胶粘支撑时的1/7，采用支座支撑的光学元件下表面面形RMS 值小于三点胶粘支撑时的1/8。

可以看出，相对于传统的三点胶粘支撑方式，运动学支撑方式在抵消外界热载荷冲击的性能上具有明显的优势。

4.2 外界应变对面形的影响

由于机械加工、装配精度的限制，3 处支撑台与光学元件的接触端面之间存在一定的平面度公差，公差范围在几个微米的量级。3 个支撑面平面度公差会对光学元件产生弯矩，从而影响光学元件表面面形。同样，在光刻投影物镜的工作过程中，调整力也会以应变的方式传到光学元件本身，导致光学元件上下表面面形精度劣化。

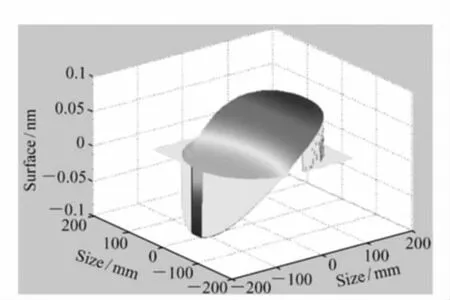
图13 公差5 μm 时上表面面形Fig.13 Top surface form with tolerance of 5 μm

图14 公差5 μm 时下表面面形Fig.14 Bottom surface form with tolerance of 5 μm

在分析过程中对其中一个支座施加沿光轴方向的强制位移以模拟外界传入的应变对光学元件表面面形的影响。在提取面形时，去除光学元件刚体位移，上下表面面形变化如图13、图14 所示。

如图15、图16 所示，上下表面面形PV 值和平面度公差基本呈线性关系，公差为5 μm 时，上下表面面形PV 值小于0.2 nm，RMS 值小于0.05 nm。

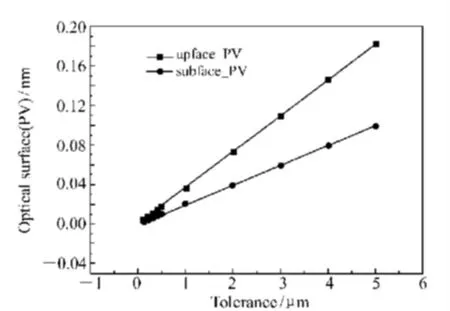
图15 上下表面PV 值随公差变化情况Fig.15 Surfaces＇ PV values vs tolerance variation

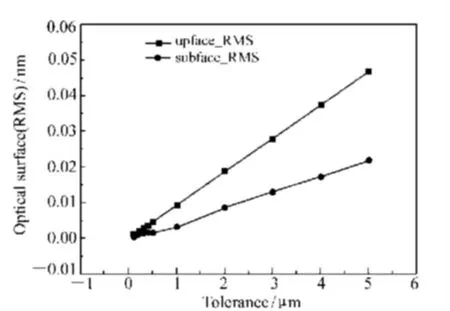
图16 上下表面RMS 值随公差变化情况Fig.16 Surfaces＇ RMS values vs tolerance variation

将光学元件在不同公差情况下的面形与传统三点底部胶粘固定的支撑方式相比较。光学元件面形变化的PV 值对比如图17 所示，采用运动学方式支撑的光学元件上表面面形PV 值小于三点胶粘支撑时的1/10，采用支座支撑的光学元件下表面面形PV 值小于三点胶粘支撑时的1/30。

光学元件面形变化的RMS 值对比如图18 所示。采用支座支撑的光学元件上表面面形RMS值小于三点胶粘支撑时的1/6，采用支座支撑的光学元件下表面面形RMS 值小于三点胶粘支撑时的1/37。

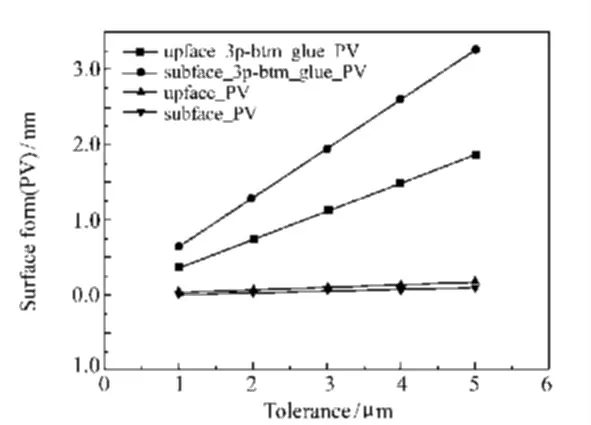
图17 运动支撑结构与三点胶粘支撑结构的面形PV 值比较Fig.17 Comparison of PV value curve vs tolerance by kinematic supporting structure and 3-point glue supporting structure

图18 运动支撑结构与三点胶粘支撑结构的面形RMS 值比较Fig.18 Comparison of RMS value curve vs tolerance by kinematic supporting structure and 3-point glue supporting structure

可见采用支座的支撑方式能够很好地改善加工误差对光学表面面形的影响，尤其对于支撑接触的下表面面形效果更为突出。

5 结 论

光学元件支撑结构对光刻投影物镜成像性能的影响非常关键。为了消除温度变化、外界应变等因素对光学元件表面面形的影响，本文提出了一种新型的运动学支撑结构。该支撑结构设计简单，无须使用铟钢等特殊材料即可实现消热应变功能。设计了支座径向柔度，并与有限元分析结果比较，验证了支座径向柔度理论计算方法的正确性。此支座柔度计算方法可以进一步指导选取不同光学元件运动学支撑结构的主要参数和尺寸。

着重分析了所提出的支撑结构抵抗外界温度和平面度加工误差对光学元件表面面形的影响。结果表明:该支撑结构能够有效消除外界温度的影响，面形变化的RMS 值优于采用三点胶粘固定方式时的1/7; 加工制造误差或者装配应力对面形的影响也可通过改支撑方式进行有效消除，面形变化的RMS 值优于采用三点胶粘固定方式时的1/6，下表面面形的改善尤其显著。

实际工作过程中，光刻投影物镜的温度变化往往控制在±0.1 ℃以内，此时的面形变化RMS值远小于1 nm; 将平面度误差控制在5 μm 以内时，由于支座吸收了大部分变形，光学元件的面形几乎不受影响。该支撑机构能够满足工作过程中光刻投影物镜系统对于光学元件表面面形精度动态稳定性的要求。

［1］ FUKAGAWA Y，SHINANOY J，NAKAMORIM M. Optimum adjustment for distortion in semiconductor lithography equipment［J］.J． Advanced Mechanical Design Systems and Manufacturing，2008，2(3) ：378-382.

［2］ SHINANO Y，FUKAGAWA Y，TAKANOY Y，et al.. Lens system adjustment in semiconductor lithography equipment：optimization for lens groups rotation［J］.J． Advanced Mechanical Design Systems and Manufacturing，2008，2(5) ：844-852.

［3］ YOSHINARA T，KOIZUMI R，TAKAHASHI K，et al.. Realization of very-small aberration projection lenses［J］.SPIE，2000，4000：559-566.

［4］ 鲁亚飞，范大鹏，范世珣，等.快速反射镜两轴柔性支撑设计［J］.光学 精密工程，2010，18(12) :257412582.LU Y F，FAN D P，FAN SH X，et al.. Design of two-axis elastic support for fast steering mirror［J］.Opt． Precision Eng．，2010，18(12) :2574-2582.( in Chinese)

［5］ 王忠素，翟岩，梅贵，等.空间光学遥感器反射镜柔性支撑的设计［J］.光学 精密工程，2010，18(8) :1833-1841.WANG ZH S，ZHAI Y，MEI G，et al.. Design of flexible support structure of reflector in space remote sensor［J］.Opt．Precision Eng．，2010，18(8) :1833-1841.( in Chinese)

［6］ 沙巍，张星祥，陈长征，等.圆形反射镜无隙支撑方法的应用［J］.光学 精密工程，2010，18(10) :2199-2205.SHA W，ZHANG X X，CHEN CH ZH，et al.. Application of zero clearance support method based on circle mirrors［J］.Opt． Precision Eng．，2010，18(10) :2199-2205.( in Chinese)

［7］ AHMAD A.Optomechanical Engineering Handbook［M］. Boca Raton:CRC Press，1999.

［8］ WATSON D C. Kinematic optical mounting assembly with flexures:US:6，922，293［P］. 2005-07-26.［9］ SPINALI. Kinematic optical mounting:US:6，400，516［P］. 2002-06-04

［10］ MATSUYAMA T，OHMURA Y，WILLIAMSON D M. The lithographic lens: its history and evolution［J］.SPIE，2006，6154:615403.

［11］ 吴鹰飞，周兆英.柔性铰链的设计计算［J］.工程力学，2002，19(6) :136-140.WU Y F，ZHOU ZH Y. Design of flexure hinges［J］.Eng． Mechanics，2002，19(6) :136-140.( in Chinese)

［12］ 朱仁胜，沈健，谢祖强，等.双轴柔性铰链柔度的设计计算［J］.合肥工业大学学报，2009，32(9) :1370-1373.ZHU R S，SHEN J，XIE Z Q，et al.. Design calculation of double-axis flexure hinges［J］.J． Hefei University of Technology( Natural Science) ，2009，32(9) :1370-1373.( in Chinese)

［13］ YONG Y K，LU T F. Kinetostatic modeling of 3-RRR compliant micro-motion stages with flexure hinges［J］.Mechanism and Machine Theory，2009，44(6) :1156-1175.

［14］ 陈伟，丁亚林，惠守文，等.碳化硅扫描反射镜支撑结构设计［J］.中国光学，2012，5(2) :161-166.CHEN W，DING Y L，HUI SH W，et al.. Design of kinematic mount for SiC scanning reflective mirror［J］.Chinese Op-tics，2012，5(2) :161-166.( in Chinese)