首次积分法及其在非线性发展方程中的应用

刘文健，丁春晓，桑 波

首次积分法及其在非线性发展方程中的应用

*刘文健，丁春晓，桑 波

（聊城大学数学科学学院，山东，聊城 252059）

通过结合李群理论和微分系统的首次积分，提出了一种扩展的首次积分法。利用此方法并借助符号计算Maple和吴氏消元法得到了变系数ANNV方程的一些新的精确解。

首次积分法；变系数ANNV方程；延拓；对称；精确解；吴氏消元法

求非线性偏微分方程的精确解是孤立子理论中的重要内容之一。对于不同类型的方程有不同的求解方法，如：F-展开法，tanh函数法，三角函数法，指数函数法，李群方法，齐次平衡法[1-7]等。在2002年，冯兆生提出了用首次积分方法[8-9]求解非线性偏微分方程的精确解。它的独特之处在于应用了可交换代数理论。首次积分方法是对非线性偏微分方程进行行波变换，化成常微分方程。用可交换代数理论可求出一阶常微分方程组的首次积分。在本文中利用李群求解非线性偏微分方程的基本思想，通过构造群不变量作为函数变换的基础，将偏微分方程化为常微分方程。由李群导出的变换为非行波变换，再结合常微分系统的首次积分的定义来求解非线性偏微分方程的精确解。并利用此方法得到了变系数ANNV方程一些新的精确解。本文与文献[10]的最大区别在于在首次积分方法中引进了李群理论和研究了不同的方程。下面定义微分方程的首次积分。

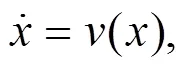
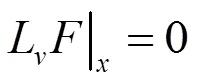
1 首次积分法

下面是新的首次积分法的主要步骤。

给定非线性偏微分方程

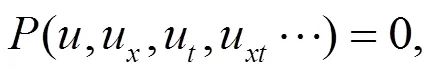
首先运用李群方法构造不变量作为非行波变换，将其约化为常微分方程

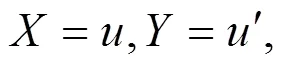
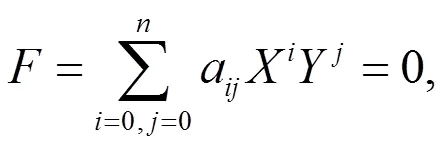
2 ANNV方程的精确解

对于(2+1)维变系数ANNV系统[12-15]

设单参数群的生成元为

因此(9)式的四阶延拓为

其中

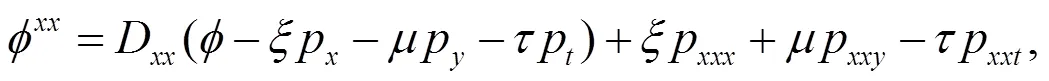
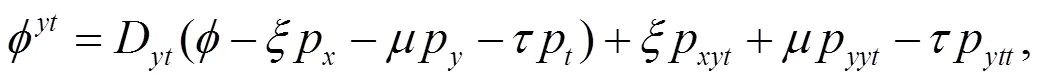
将(11)式和(8)式代入方程(12)中，解这个方程可得生成元为

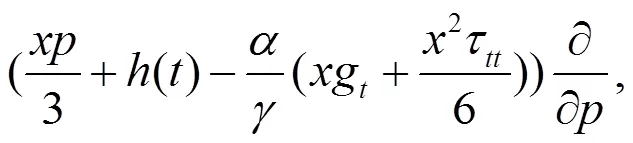
由(13)式可得相应的特征方程为

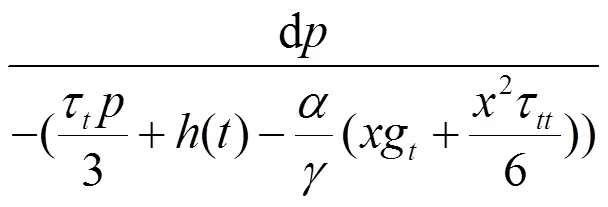
其约化方程为

其对应的约化方程为

其对应的约化方程为

为了得到常微分方程，对上述三种情况进行再次约化，用对称的方法得到不变量和约化方程。

对于情况1非线性发展方程(15)的对称可设为

其对应的特征方程为

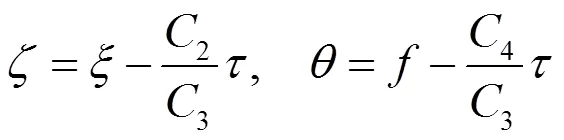
约化方程为

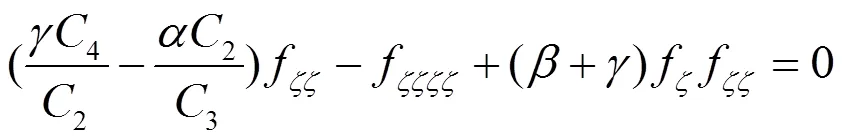
相似的，对于非线性发展方程(16)和(17)的特征方程分别为

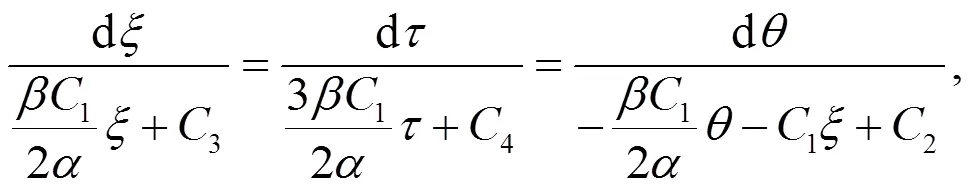
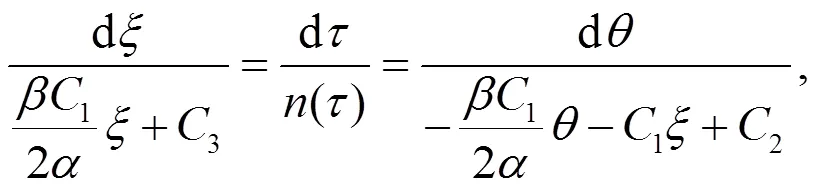
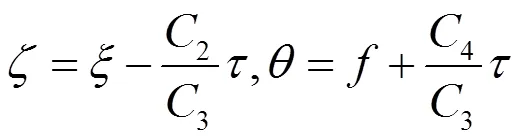
约化方程为

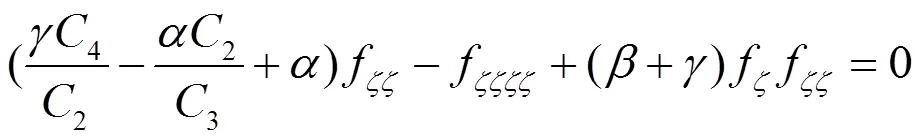
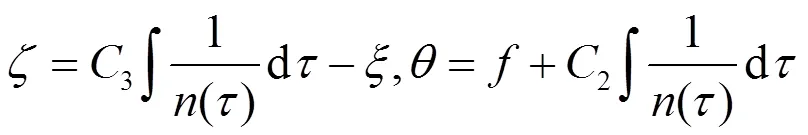
约化方程为

下面用首次积分的方法来解常微分方程(20)，(23)和(24)。

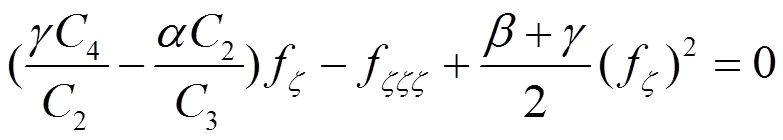
假设系统(27)的多项式首次积分为

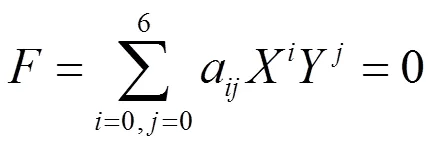
去解此方程组可得

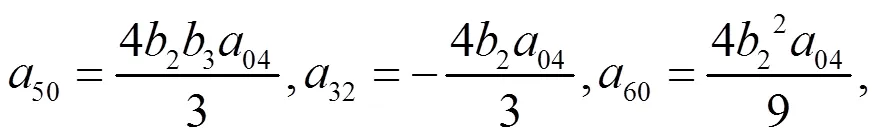
其中在(28)式中，其它系数为零，且

将(29)带入到(28)式，可得系统(27)的首次积分为

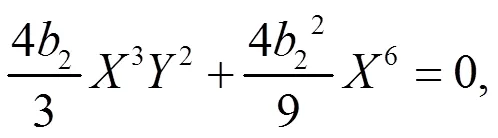
其中

其中

其中

相似的，用上述同样的方法来解方程（23）和(24)，可得原方程(8)的解分别为

其中

其中

其中

其中

其中

其中

3 结论

本文结合首次积分方法的思想，通过李群理论和微分系统的首次积分，提出了一种新的首次积分法。用李群中的延拓和对称方法和修正的CK方法都能得到不变量来构造非行波变换，用这种非线性变换所得到的结果比一般的行波变换要广泛的多。而且用这种微分系统首次积分的定义法来求得的首次积分要比可交换代数理论求得的也要广泛。为了说明方法，利用此首次积分方法得到了ANNV方程的一些新的精确解，这些解在所见到的文献中还未出现过。

[1] Abdou M A. The extended F-expansion method and its application for a class of nonlinear evolution equation[J]. Chaos, Soliton Fract, 2007,31:95-104.

[2] Wazwz A M. The tanh method for travelling wave solution of nonlinear wave equations[J]. Appl. Math. Comput,2007, 187(2):1131-1142.

[3] 刘娜,刘希强.两类非线性发展方程的新的显式解[J]. 数学的实践与认识, 2008,38(20):189-193.

[4] XIN Xiangpeng, ZHANG Linlin. Symmetry reductions and exact solutions of a ( 2+ 1)-dimensional nonline-ar evolution equation [J].Journal of Shandong University : Natural Science, 2009,22(4):16-20.

[5] 郭美玉,刘希强,高洁.(3+1)-维Zakharov-Kuznetsov方程的对称及约化[J].山东大学学报:理学版，2009, 44(6):91-97.

[6] ZHANG Linlin, XIN Xiangpeng.Exact Solutions of the (2+1)-dimensional Modified KP Equation[J]. Journal of Liaocheng University: Natural Science,2009,22(3):9-13.

[7] Wang M L. Exact solutions of a compound KdV-Burgers equation[J]. Phys. Lett. A 1996, 213:279-287.

[8] Feng Z S. The first-integral method to study the Burgerd-KdV equation[J]. J Phys A: Math Gen,2002, 35:343-349.

[9] Feng Z S, Wang X H. The first-integral method to the two-dimensional Burgerd-KdV equation[J]. Phys Lett A, 2003, 308:173-178.

[10] 刘文健，桑波. 首次积分法及其在非线性发展方程中的应用[J]. 聊城大学学报，2011, 24(2):13-17.

[11] V阿诺尔德I. 常微分方程[M]. 沈家骐等译. 北京：科学出版社,2001:76-77.

[12] ZHANG Lihua, LIU Xiqiang. Symmetry, Reductions and New Exact Solutions of ANNV Equation Through Lax Pair[J]. Commun. Theor. Phys., 2008, 50:1-6.

[13] WANG Ling, LIU Xiqiang. Symmetry Reductions, New Exact Solutions and Conservation Lax of ANNV Equation[J]. Commun. Theor. Phys., 2008, 49:1-8.

[14] Boiti M, Leon J J P, Manna M, et al.On the spectral transform of a Korteweg-de Vries equation in two spatial dimensions[J]. Invers Probl., 1986, 2: 271-274.

[15] Qian X M, Lou S Y. Variable Separation Approach for a Differential-difference Asymmetric ANNV Equa tion[J]. Z.Naturforsch., 2004, 59a:645-658.

THE FIRST INTEGRAL METHOD AND ITS APPLICATIONS IN NONLINEAR EVOLUTION EQUATIONS

*LIU Wen-jian, DING Chun-xiao, SANG Bo

(School of Mathematics Science, Liaocheng University, Liaocheng , Shandong 252059，China)

A generalized first integral method is proposed by studying Lie group theory and first integral of differential system. The method is applied ANNV equation with variable-coefficients. Furthermore, some new exact solutions are obtained based on the Maple and Wu method.

first integral method; variable-coefficients ANNV equation; prolongation; symmetry; explicit solutions

0175

A

10.3969/j.issn.1674-8085.2012.04.001

1674-8085(2012)04-0001-05

2012-01-22；

2012-04-26

国家自然科学基金项目(11076015)

*刘文健(1985-)，男，山东高唐人，硕士研究生. 主要从事微分方程理论及应用研究(E-mail: liuwenjian198504@126.com);

丁春晓(1987-)，女，山东聊城人，硕士研究生. 主要从事不确定信息处理研究(E-mail: dingchunxiao1987@163.com);

桑 波(1976-)，男，山东肥城人，副教授，主要从事微分方程理论及应用研究(E-mail: xiaozaimengzhong@126.com).