基于层次分析法的服装面料性能模糊综合评价

凌 雪

基于层次分析法的服装面料性能模糊综合评价

凌 雪

(安徽工程大学人文学院，安徽，芜湖 241000)

为了全面评价服装面料的各项性能指标，采用层次分析法与模糊综合评价相结合的评价方法。首先，建立了服装面料综合性能的评价指标体系，利用层次分析法确定了各项性能指标的权重系数。然后，运用模糊综合评判法对其各项性能指标进行评价，使得对服装面料综合性能的评价具有准确性和客观性。具体实例验证了层次分析法与模糊综合评价相结合的合理性与有效性。

层次分析法；服装面料；综合性能；模糊综合评价

面料、款式、色彩是服装的三要素，其中面料是关键，它始终贯穿于人类的服装发展，每一次新面料的出现都会给服装带来与众不同的变化[1]。目前，市场上的服装面料种类繁多、性能指标多样，如何评价服装面料的综合性能是服装设计师在选择面料时所面临的一个重要问题，因为面料选择合适与否直接影响服装的穿着效果。就具体的实际应用而言，只考虑某一方面或者某几个方面的性能指标是不够全面的，所以在选择服装面料时，应对其综合性能进行全面考察。

鉴于服装面料的综合性能评价所涉及的指标因素多，而且一般是定性的，无法利用定量的方法直接进行对比分析，因具有鲜明的模糊性，因而服装面料的综合性能评价是一个多层次的模糊综合评判问题。自从美国学者Zadeh教授于1965年提出模糊集合[2]的概念以来，模糊数学理论在近几十年内发展迅速，基于模糊数学理论的模糊综合评判法也因此取得很大的进展，并在工程领域得到广泛地成功应用[3-4]。查阅国内资料，对于服装面料综合性能进行模糊评判研究的文献甚少。为此，本文引入模糊综合评价法对服装面料综合性能进行全面地分析。

1 多级模糊综合评价

多级模糊评价模型由评价因素集、评价集、因素权重集、隶属函数及单因素评价矩阵、模糊操作算子等几部分组成[3,5]。

1.1 建立因素集与评价集

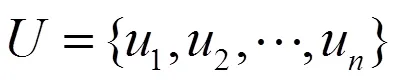
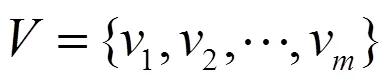
1.2 模糊评价

首先从因素集中的单个因素出发进行评价，确定评价对象对因素集中各元素的隶属程度。然后将个因素的评价集组成一个总的评价矩阵，通常以表示。

1.3 建立权重向量

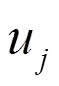
1.4 模糊综合评价数学模型

当权重向量A和评判矩阵为已知时，便可做模糊变换来进行综合评判，模糊综合评判的数学模型为

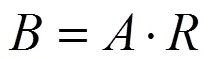
图1所示的是二级模糊综合评判模型的框图[3]。

若一级因素集X仍含有较多的因素，还可将X再细分，于是得到三级模糊综合评判模型、四级模糊综合评判模型等等[6]。

2 服装面料综合性能评价模型

2.1 建立服装面料性能指标评价体系

服装面料除要求其基本服用性能(保健护肤、抗菌、抗污染等)优异外，还要求其具有良好的运动舒适性，能够导湿、透气，迅速将人体运动时产生的汗液和汗气吸附到织物外层并迅速蒸发，使衣服不沾身；同时，还要求其具有抗静电性，避免织物与身体或与其他物体的接触摩擦产生静电；如果是户外运动，还要求其具有一定的防紫外线功能，以免过强的紫外线伤害皮肤；另外，还需要考虑该面料的经济性(成本低、生产工艺复杂性与否等)。综合以上各种因素，将服装面料综合性能指标主要分为功能性指标、舒适性能指标、基本服用性能指标、经济性能指标，运用层次分析法的思想建立了如图2所示的评价指标体系。服装面料综合性能评价指标体系分两个层次，第一层为总目标因素集={1,2,3,4}；第二层为子目标因素集1={11,12,13,14}，2={21,22}，3={31,32,33,34}，4={41,42}。

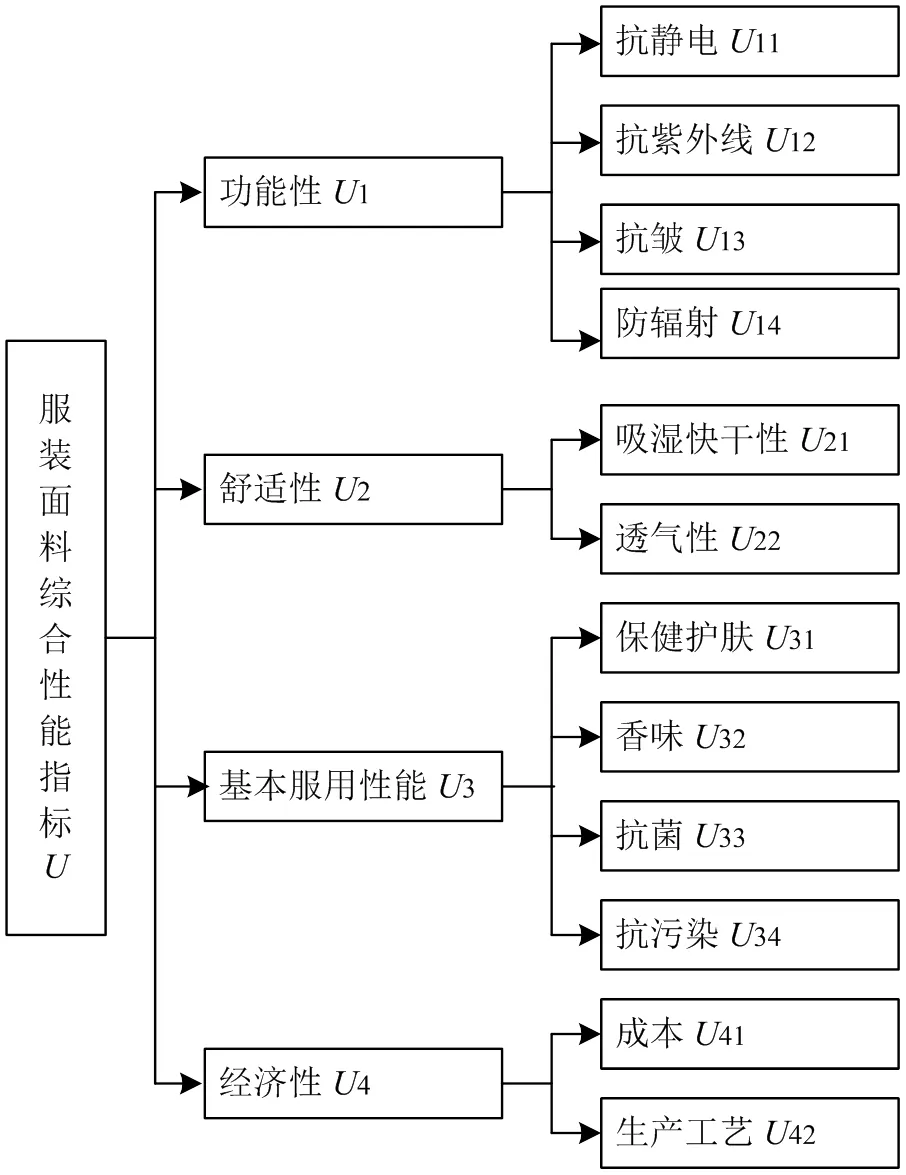
图2 服装面料性能指标体系

2.2 服装面料性能综合性能评价的评价集

评价集是评价人员对各层次评价指标所给出的评语集合，对于不同的评价指标，其评语等级所代表的含义各不相同。根据服装面料各项性能指标的特点，给出评价集={v}，共设5个评价等级，即={1,2,3,4,5}，其中1＝{优秀}，2＝{良好}，3＝{中等}，4＝{一般}，5＝{较差}，即服装面料性能指标的评价集为V＝{优秀，良好，中等，一般，较差}。

2.3 确定服装面料性能各级指标权重系数

在进行服装面料性能模糊综合评判时，各项指标的权重系数对最终的评判结果将会产生很大的影响，不同的权重系数会导致不同的评判结果，因此正确确定权重系数显得尤为重要。确定权重系数的方法很多，本文拟采用层次分析法(analytical hierarchy process, AHP)[7]来确定各指标权重系数。

2.3.1构建判断矩阵

建立判断矩阵是层次分析法最关键的一步，针对每层每项的各下属因素(例如目标层的各下属因素指标1、2、3、4)两两进行比较来确定矩阵中各元素的值，其判断标准按表1给出元素相对于元素的重要性比例标度a。显然，元素相对于元素的重要性比例尺度a＝1/a。这样，个元素对于所属的上一层元素便可构成一个以重要性标度a为元素的两两比较判断矩阵＝(a)×，本文判断矩阵中各个元素的值由服装设计领域的专家组根据服装面料的各性能指标的重要程度结合表1给出。

表1 判断尺度标度

通过该领域的专家建立两两比较判断矩阵如式(1)~ (5)所示。其中，1是目标层U的各下属因素(1,2,3,4)的两两比较判断矩阵；21、22、23和24分别是1、2、3和4各下属因素的两两比较判断矩阵。

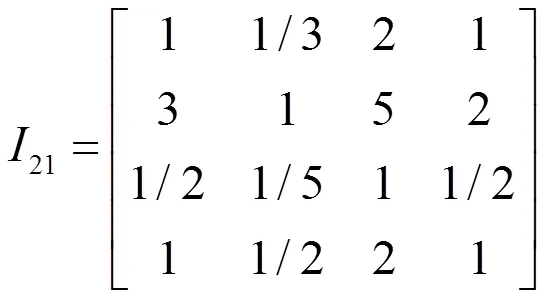
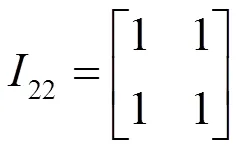
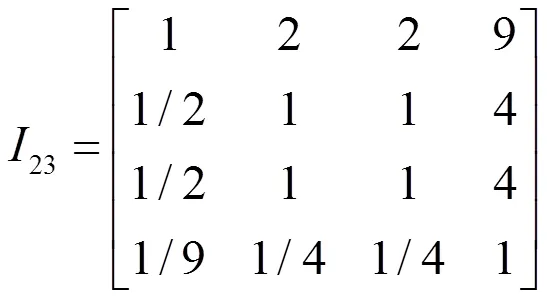
2.3.2求解各级指标的相对权重向量

3 应用实例

目前市场上常见的服装面料主要有：棉织、麻织物、毛织物、丝绸织物、化学纤维面料、针织品类面料、裘皮及皮革面料等。其中，化学纤维面料质地均匀细洁，色泽艳丽，手感滑爽，穿着舒适，透气性及悬垂性好，适用于夏季女衣裙、衬衫、冬季棉衣和童装等衣料。本文以该面料为研究对象，运用二级模糊综合评判法对其性能指标进行分析评价。

3.1 建立单因素模糊评价矩阵

为了使该人造棉织物面料综合性能的评判结果具有尽可能高的客观性，我们采用问卷调查法和专家打分对二级指标中的各个因素进行评价，通过对调查结果进行整理和统计，最终得到如表2所示的评价结果。

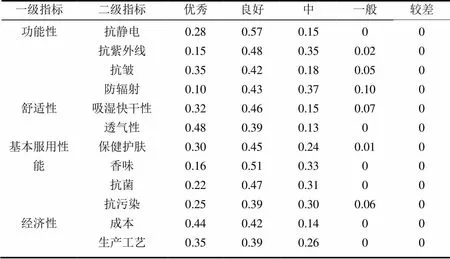
表2 评价结果统计表

由此求得二级单因素模糊综合评价矩阵：

3.2 各项性能的模糊综合评判

根据本文所求得的二级指标权重向量即可求得一级指标模糊综合评判结果：

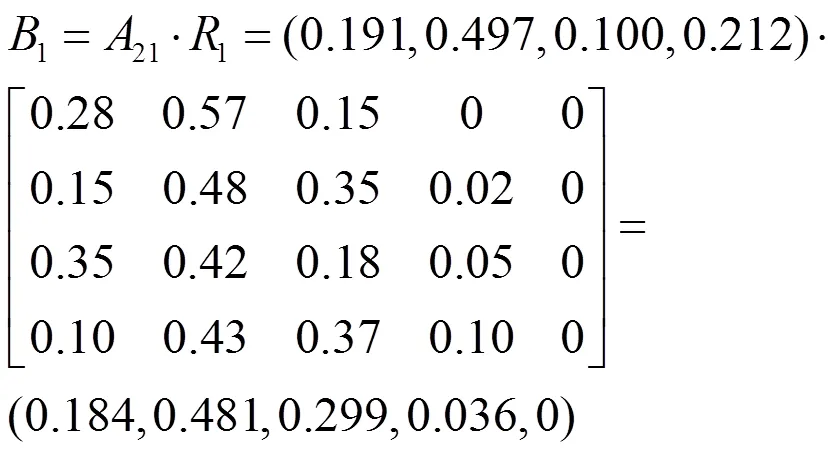
同理可以求得：

由评判结果可知该面料的功能性指标、舒适性指标、基本服用性能指标和经济性指标的隶属度分别为48.1%、42.5%、46.5%和41.1%，分别对应功能性良好、舒适性良好、基本服用性能良好和经济性优秀。

再根据一级指标的权重向量

该化学纤维面料模糊综合性能评判结果为：

根据以上结果，则该化学纤维面料综合性能总指标评价结果为良好，其隶属度为48.1%。

4 结论

(1) 为了避免层次分析法中人的主观判断、偏好等对服装面料性能的影响，采用层次分析法与模糊综合评判相结合的方法建立了服装面料模糊综合评价数学模型。

(2) 通过对某化学纤维面料的综合模糊评价，验证了采用层次分析法与模糊综合评判相结合进行服装面料模糊综合评价的合理性与可靠性。

(3) 由于层次分析法与模糊综合评判具有计算简单、易于实现等优点，有利于快速有效地评价服装面料综合性能指标，可作为服装设计师在选择不同服装面料型号时提供一定的参考价值，对于其它与服装行业相关方面的综合性能的科学评价也具有借鉴作用。

[1] 刘珍珍,陈超.层次分析法在服装面料选择中的应用[J].苏州大学学报:工科版,2008, 28(3): 47-50.

[2] Zadeh L. A fuzzy sets [J]. Information and control, 1965(8):338-353.

[3] 刘世豪,叶文华,唐敦兵,等.基于层次分析法的数控机床性能模糊综合评判[J].山东大学学报:工学版,2010, 40(1):68-73.

[4] 李鲲鹏,胡虔生.电机设计方案的多级模糊综合评判[J].微电机,2002,35(1):11-14.

[5] 韩立岩,汪培庄.应用模糊数学[M].北京:首都经济贸易大学出版社,1998.

[6] 朱剑英.智能系统非经典数学方法[M].武汉:华中科技大学出版社,2001.

[7] 许树柏.层次分析法原理[J].天津:天津大学出版社,1998.

FUZZY COMPREHENSIVE EVALUATION FOR THE PERFORMANCE OF CLOTHING FABRIC BASED ON ANALYTICAL HIERARCHY PROCESS

LING Xue

(School of Humanities, Anhui Polytechnic University, Wuhu, Auhui 241000, China)

In order to evaluate each performance index of clothing fabric comprehensively, an approach based on the analytical hierarchy process (AHP) and fuzzy comprehensive evaluation is presented. Firstly, an evaluation index system for comprehensive performance of clothing fabric is established, the weight of each performance index is determined by using AHP. Furthermore, a fuzzy comprehensive evaluation method is used to evaluate each performance index in order that the overall performance evaluation of clothing fabric is accurate and objective.A specific example shows that the fuzzy comprehensive evaluation based on AHP is reasonable and effective.

analytical hierarchy process; clothing fabric; comprehensive property; fuzzy comprehensive evaluation

TU984

A

10.3969/j.issn.1674-8085.2012.04.020

1674-8085(2012)04-0084-04

2012-01-08；

2012-04-05

凌 雪（1982-)，女，安徽六安人，助教，硕士，主要从事智能服装方面的研究(E-mail:lingxue1982@126.com).