一类带非经典热方程的单相Stefan问题

闫德宝

（菏泽学院 数学系，山东 菏泽274000）

一类带非经典热方程的单相Stefan问题

闫德宝

（菏泽学院 数学系，山东 菏泽274000）

证明了一类带非经典热方程的单相Stefan问题局部解的存在唯一性．首先利用Green恒等式将问题转化为等价的积分方程组，再由压缩映照原理得到了问题的局部解．最后，证明了解对初值的稳定性．

Stefan问题；存在唯一性；压缩映照原理；局部解；稳定性

0 引言

Stefan问题是一种常见于物理、化学等领域的自由边界问题．文献［1－4］讨论了带经典热方程的Stefan问题和其解的存在唯一性；近年来，文献［5－8］讨论了带非经典热方程的单相Stefan问题，包括解的存在唯一性和渐进性等问题；文献［9－10］在探讨Stefan问题的基础上，给出了一些开问题．本文讨论一种带非经典热方程的单相Stefan问题，包括该问题局部解的存在唯一性和解对初值的稳定性．本文的模型如下：

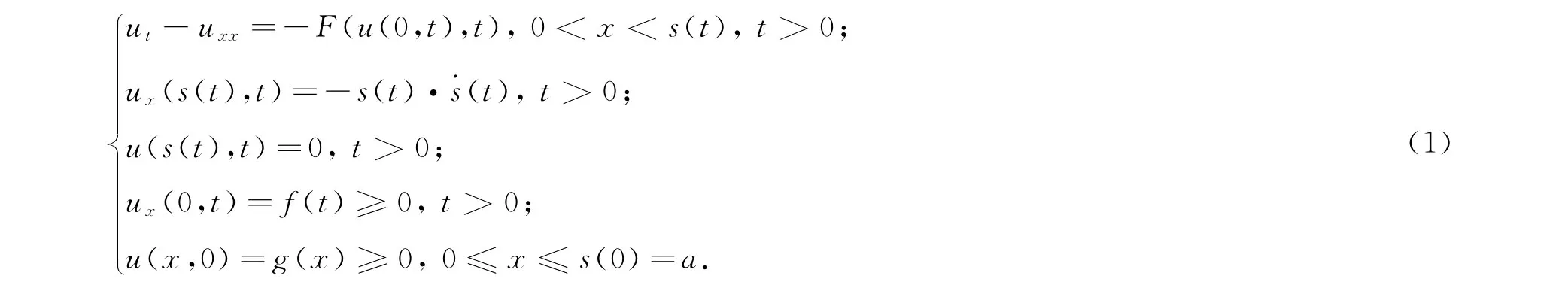
其中u＝u（x，t）表示液相的温度，s＝s（t）表示自由边界．以下为本文的几点假设：（HA）函数f（t）在R＋上连续；（HB）函数且满足下列条件：（HC1）对某常数 M ＞0及使得

1 若干引理及其证明

引理1 令ux（s（t），t）＝α（t），u（0，t）＝β（t），问题（1）与下述 Volterra型积分方程组等价：

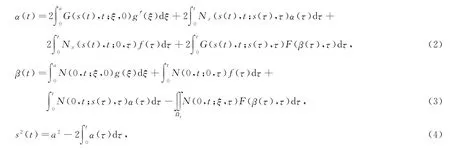
引理1的证明可参见文献［5，9］．

在以下引理的证明过程中，常用到下述不等式：

引理4 若σ≤1，M ≥1，F，f（t），g（x）满足假设条件（HA）、（HB）、（HC1）和（HC2），则在引理2的假设下，有如下性质成立：

证明 （9）—（11）式和（13）—（15）式的证明参见文献［5－7］，下面证明（12）和（16）式．首先，由及假设条件（HC1）和（HC2）有

引理5 在假设条件（HA）、（HB）、（HC1）和（HC2）及引理3的条件下，下述性质成立：

证明 （17）、（19）和（21）式的证明参见文献［5－7］，下证（18）、（20）和（22）式．对（18）式，由微分中值定理知，存在s1（t）和s2（t）之间的一函数c（t），使得

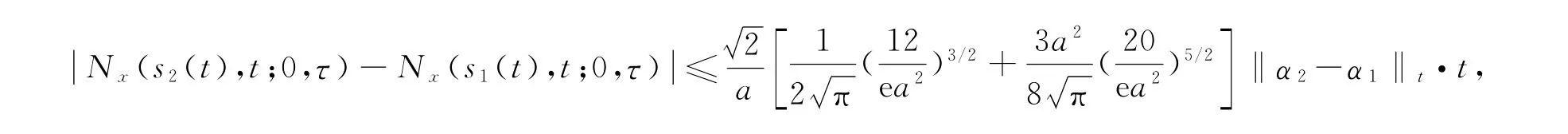
所

联立（23）和（24）式即证得（20）式．对（22）式，有

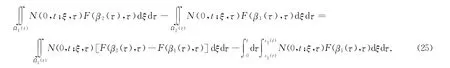
联立（25）—（27）式即证得（22）式．

引理6 在问题（1）中，设si（t）是相应于初始函数gi（x）的自由边界（i＝1，2），则有

对（30）式右端第2项，利用文献［7］中的（34）式，有

联立（30）—（32）式即得（29）式．

2 主要结果及其证明

定理1 在条件（HA）、（HB）、（HC）、（HC1）和（HC2）下，映射φ∶SM，σ→SM，σ在SM，σ上是压缩的，若M和σ满足如下条件：其中则积分方程组（2）—（4）在SM，σ上存在唯一解（α（t），β（t），s（t））．同时，问题（1）存在唯一局部解．证明 由引理4及定理1中的条件①—③，有

故在SM，σ上φ是压缩的．由此知φ在SM，σ上存在唯一不动点，即为积分方程组（2）—（3）的唯一局部解（α（t），β（t）），而s（t）的唯一性由（4）式可得．由引理1知，原问题（1）存在唯一局部解（u（x，t），s（t））．

定理2 设gi（x）∈ ［0 ，a］，i＝1，2，则问题（2）—（4）具有下述意义下的稳定性：∀ε ＞0，存在η ＞0，当 ‖g2－g1‖ ≤η，‖g′2－g′1‖ ≤η时，有 ‖（α2（t）－α1（t），β2（t）－β1（t））‖ ＜ε．从而问题（1）在上述意义下也是稳定的．

证明 利用（2）、（17）、（18）、（20）及（29）式有

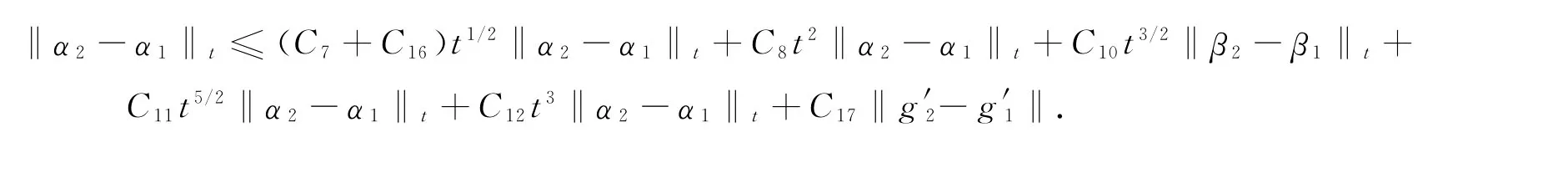
故φ是SM，σ上的映射．下证φ是压缩的，由引理5及定理1中的条件①和④得

由σ≤1有

其中J4＝C7＋C8＋C10＋C11＋C12＋C16．同理，利用（3）、（21）、（22）及（28）式得

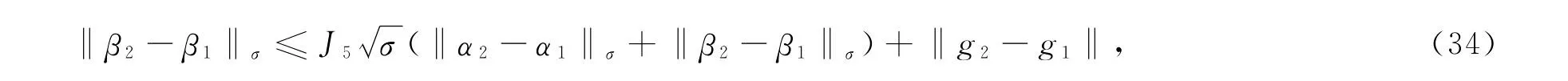
其中J5＝C13＋C14＋C15．利用（33）和（34）式可得

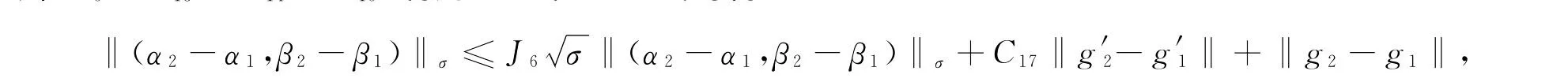
其中J6＝J4＋J5．注意到J3与J6的关系，由定理1中的条件④有

定理2得证．

［1］ Friedman A．Free boundary problems for parabolic I［J］．Melting of Solids J Math Mech，1959，8（4）：499－517．

［2］ Friedman A，Kinderlehret．A one phase Stefan problem［J］．Indiana Univ Math J，1975，24：1005－1035．

［3］ Hanzawa E I．Classical solutions of the Stefan problem［J］．Tohoku Math Journ，1981，33：297－335．

［4］ HSIEH C K．Exact solutions of Stefan problems for a heat front moving at constant velocity in a quasi－steady state［J］．Int J Heat Mass Transfer，1995，38：71－79．

［5］ Briozzo A C，Tarzia D A．Existence and uniqueness for one－phase Stefan problems of non－classical heat equations with temperature boundary condition at a fixed face［J］．EJDE，2006，21：1－16．

［6］ Briozzo A C，Tarzia D A．Convergence of the solution of the one－phase Stefan problem when the heat transfer coefficient goes to zero［J］．J Math Anal Appl，2012，389（1）：138－146．

［7］ Briozzo A C，Tarzia D A．A Stefan problem for a non－classical heat equation with a convective condition［J］．Appl Math and Comput，2010，217（8）：4051－4060．

［8］ Briozzo A C，Tarzia D A．Existence，uniqueness and an explicit solution for a one－phase Stefan problem for a nonclassical heat equation［J］．Inter Series of Numerical Math，2006，154：117－124．

［9］ Friedman A．抛物型偏微分方程［M］．夏宗伟，译．北京：科学出版社，1984．

［10］ Borodin M A．Stefan problem［J］．J Math Sci，2011，178（1）：17－54．

On a kind of one－phase Stefan problem with non－classical heat equation

YAN De－bao
（Department of Mathematicas，Heze University，Heze 274000，China）

Existence and uniqueness of local solution for a one－phase Stefan problem with non－classical heat equation are proved．Firstly，by translatting the Stefan problem into an equivalent system of integral equations with the Green Identity，we obtain the existence and uniqueness of local solutions to the integral equations by contraction mapping theorem．Finally，the stability of the solution about initial value is given．

Stefan problem；existence and uniqueness；contraction mapping theorem；local solution；stability

O175．2

A

1004－4353（2012）03－0177－06

20120424 作者简介：闫德宝（1980—），男，讲师，研究方向为偏微分方程．

国家自然科学基金资助项目（11001278）；山东省教育科学“十二五”规划重点课题项目（2011GG049）；菏泽学院科研项目（XYJJKJ－3）