利用量子逻辑网络实现1→2最佳量子克隆

张大伟

（营口大学园管理委员会，辽宁 营口115014）

利用量子逻辑网络实现1→2最佳量子克隆

张大伟

（营口大学园管理委员会，辽宁 营口115014）

提出了1个利用量子逻辑网络来实现1→2最佳量子克隆的量子克隆机．该方案利用受控旋转和受控非操作来实现1→2的最佳量子克隆，并通过选择不同的旋转角度实现通用克隆、相位协变克隆和x－z面上的实态克隆．

克隆；旋转；受控非

0 引言

量子信息的出现源自于量子力学与信息技术的有效结合，量子力学为处理量子信息问题提供了强有力的工具，但也带来了一些限制．量子信息学中的非克隆理论［1］，使得量子信息学迥异于经典信息学，它意味着不可能对1个任意的输入态进行完美的克隆［2－3］．量子克隆在量子密码术和量子通信方面具有非常重要的作用［4－7］．1996年，Buzek和Hillery［2］首先提出了实现二维空间下的量子态克隆方案，细致地描述了对于1个完全未知态进行克隆的过程，其输出端可以得到保真度为5/6（≈0．833）的独立于输入态的通用克隆（UQCM）．Brub等［8］在2000年提出了对于输入信息部分未知时的相位协变克隆（PCCM），其保真度为年，樊恒等［9］提出了对于另1种输入信息部分已知时的实态克隆（RSCM），其保真度也是最近，文献［10－16］报道了多种实现量子克隆的方案，而且部分学者还利用现有的多种物理系统，提出了1→M 的量子克隆和远程克隆方案［17－18］．受Buzek等［11］网络方案的启发，本文提出了1个实现量子克隆的网络方案：利用受控旋转和受控非门操作来实现二维空间下的1→2最佳量子克隆，通过选择不同的旋转角度，3种类型的量子克隆都可以实现．

1 3种形式的最佳克隆

在量子力学中，每1个量子态都可以看成是对应布洛赫球面上的1个点，可表示为

其中α，β，φ∈［0，2π）．克隆可以理解为是向空白的量子态上复制信息的过程，对1个初始输入态的信息了解的越多，克隆的保真度就越高．目前，常见的量子克隆机有以下3种形式：

1）初始信息完全未知（α，β，φ完全未知）．此时的克隆过程称为通用量子克隆，可表示为

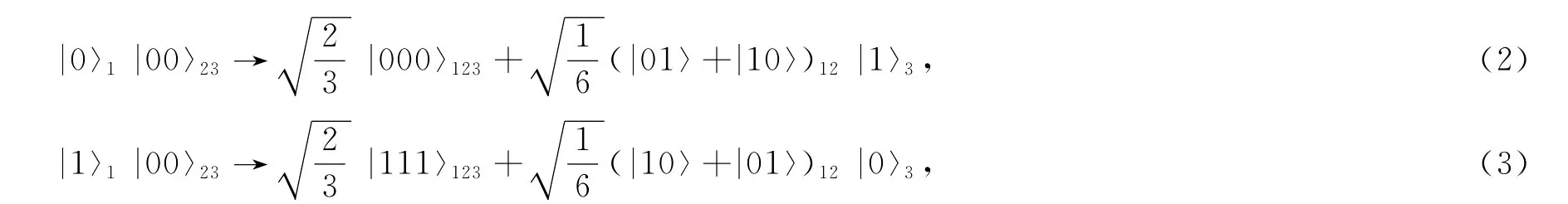
其中的角标1、2、3分别表示要克隆的粒子态、空白粒子态和辅助粒子态．输出2个粒子态1和2的约化密度算符是相同的，即

3）对于另1种克隆变换，初始条件限定于φ＝0，α，β∈［－1，1］，α和β都是实数，此时初始信息被限定在x－z赤道面上，可理解为输入态为纯态［9－10］．此时的克隆变换形式为

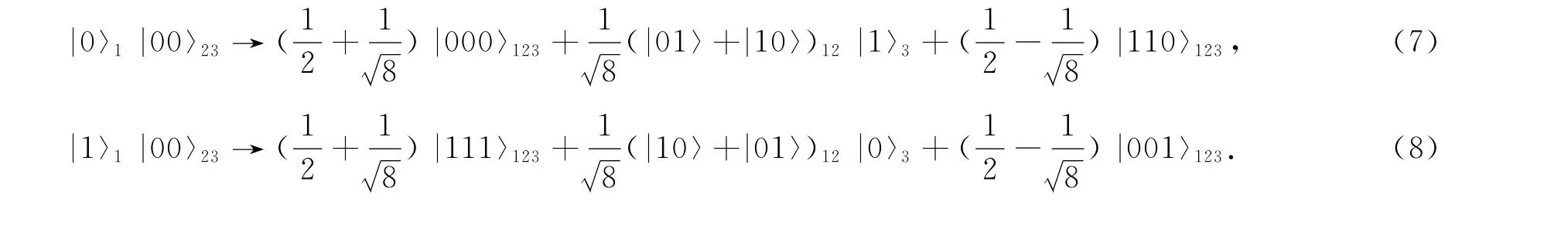
上述3种不同的克隆都是对应于不同的初始条件得到的，其保真度都是独立于输入态．

2 3种量子克隆实现方案

受文献［11］中网络方案的启发，本文提出的网络方案如图1所示，整个逻辑网络分为制备（prep）和克隆（cloning）2个部分．图中的1、2、3分别表示输入、空白和辅助粒子．

图1 最佳1→2量子克隆网络

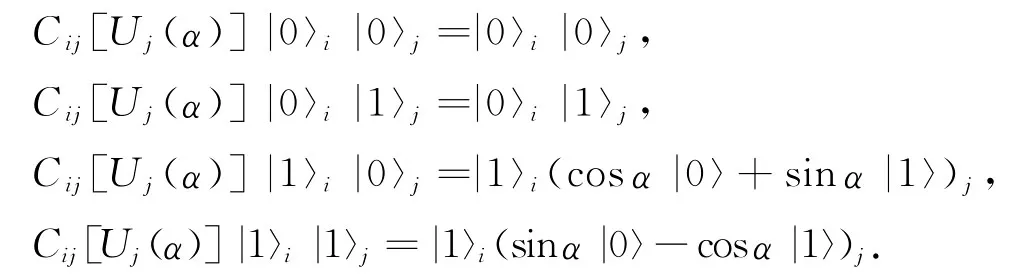
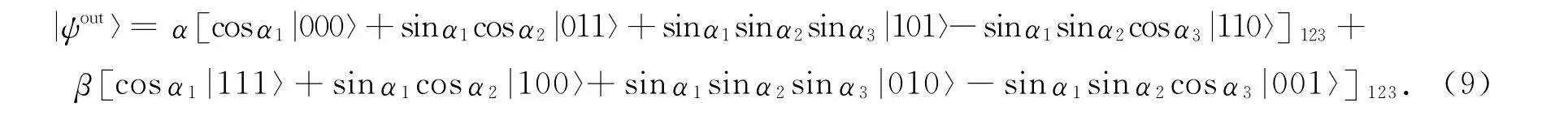
对于3种不同类型的克隆，需要对其所得态系数的角度进行确定［9］．从（9）式可以看出，量子态前的系数之间都存在着相互联系．将输出态中的系数定义为：cosα1＝a，sinα1cosα2＝b，sinα1sinα2sinα3＝c，－sinα1sinα2cosα3＝d．当选择旋转角度则输出态变为

即得到了通用量子克隆的形式．而对于均衡相位协变克隆来说，只需将旋转角度定为则系统的输出态为

此时对应的克隆形式即为最佳实态克隆．

3 结论

本文利用量子网络实现了通用量子克隆、相位协变量子克隆以及实态克隆3种不同类型的1→2最佳量子克隆．与Buzek等的方案相比，本文方案用了更少的操作．2001年，黄运峰等［19］利用极化分束器和半波片等线性光学设备实现了通用量子克隆；2002年，文献［20－21］报道了利用核磁共振技术和量子光学方法的通用克隆实验．本方案中所需要的单比特和两比特受控操作，可以通过目前所广泛应用的核磁共振技术、线性光学、腔QED技术等物理模型来实现［22－23］，因此本文方案在实验上具有可操作性．

［1］ Wootters W，Zurek W H．A single quantum cannot be cloned［J］．Nature，1982，239：802．

［2］ Buzek V，Hillery M．Quantum copying：beyond the no－cloning theorem［J］．Phys Rev A，1996，54：1844．

［3］ 段路明，郭光灿．量子态的概率克隆和认证［J］．研究快讯，1999，28（10）：35－36．

［4］ Ekert A．Quantum cryptography based on Bell’s theorem［J］．Phys Rev Lett，1991，67（6）：661－663．

［5］ Bennett C H．Quantum cryptography using any two nonorthogonal states［J］．Phys Rev Lett，1992，68（21）：3121－3124．

［6］ Pan J W，Gasparonis，Aspelmeyer M，et al．Experimental realization of freely propagating teleported qubits［J］．Nature（London），2003，421：721．

［7］ Zhao Z，Chen Y A，Zhang A N，et al．Experimental demonstration of five photon entanglement and open－destination teleportation［J］．Nature（London），2004，430：54－58．

［8］ Brub D，Cinchetti M，D’Ariano G M，et al．Phase－covariant quantum cloning［J］．Phys Rev A，2000，62（1）：012302－012307．

［9］ Fan H，Mastumoto K，Wang X B，et al．Quantum cloning machine for equatorial qubits［J］．Phys Rev A，2001，65：012304．

［10］ Gisin N，Massar S．Optimal quantum cloning machines［J］．Phys Rev Lett，1997，79（11）：2153－2156．

［11］ Buzek V，Braunstein S L，Hillery M，et al．Quantum copying：a network［J］．Phys Rev A，1997，56（5）：3446－3452．

［12］ Zhang W H，Wu T，Ye L，et al．Optimal real state cloning in d－dimensions［J］．Phys Rev A，2007，75（4）：044303－044306．

［13］ Zhu A D，Yeon K－H，Yu S－C．Optimal universal and phase－covariant cloning machines with quantum－dot spins in cavity QED［J］．J Phys B，2009，42：235501－235505．

［14］ Zhang D W，Shao X Q，Zhu A D．Quantum logic network for cloning a state near a given one based on cavity QED［J］．Chin Phys Lett，2008，25：1954．

［15］ Zhang W H，Yu L B，Ye L．Optimal asymmetric phase－covariant quantum cloning［J］．Phys Lett A，2006，356：195－198．

［16］ Zou X B，Li K，Guo G C．Linear optical scheme for implementing the universal and phase－covariant quantum cloning machines［J］．Phys Lett A，2007，366：36－41．

［17］ Meng F Y，Zhu A D，Yeon K－H，et al．Implementing 1→M economical phase－covariant cloning and telecloning in cavity QED［J］．J Phys B，2009，42：165504．

［18］ Zhou Y H，Wang L．Scheme for implementing 1→M symmetric economical phase－covariant telecloning based on quantum logic network［J］．J Mod Opt，2012，59：658－662．

［19］ Huang Y F，Wan L L，Li C F，et al．Optical realization of universal quantum cloning［J］．Phys Rev A，2001，64（1）：012315－012319．

［20］ Cummins H K，Jones C，Furze A，et al．Approximate quantum cloning with unclear magnetic resonance［J］．Phys Rev Lett，2002，88（18）：187901－187904．

［21］ Lamas－Linares A，Simon C，Howell J C，et al．Experimental quantum cloning of single photons［J］．Science，2002，296（5568）：712－714．

［22］ Song K H，Zhou Z W，Guo G C．Quantum logic gate operation and entanglement with superconducting quantum interference devices in a cavity via Raman transition［J］．Phys Rev A，2005，71（5）：052310－052313．

［23］ Shao X Q，Zhu A D，Zhang S，et al．Efficient scheme for implementing an N－qubit Toffoli gate by a single resonant interaction with cavity quantum electrodynamics［J］．Phys Rev A，2007，75（3）：034307－034310．

Implementing 1→2 optimal quantum cloning based on quantum logic network

ZHANG Da－wei
（Management Committee of Yingkou University Zone，Yingkou 115014，China）

A quantum logic network is proposed to implement 1→2 optimal quantum cloning，which compose of controlled－rotation operations and controlled－NOT operations．We can implement universal quantum cloning（UQCM），phase－covariant cloning（PCCM）and real state cloning of x－z equatorial plane（RSCM）by choosing different rotation angles．

cloning；rotation；controlled－NOT

O431

A

1004－4353（2012）03－0204－04

20120627

张大伟（1983—），男，助教，研究方向为量子信息．