模式识别中的近邻性测度
崔荣一
(延边大学工学院计算机科学与技术系 智能信息处理研究室,吉林 延吉133002)
模式识别中的近邻性测度
崔荣一
(延边大学工学院计算机科学与技术系 智能信息处理研究室,吉林 延吉133002)
模式之间的相异性或相似性的定量描述是模式识别领域中的基本问题之一.本文在论述和讨论近邻性的本质和数学定义的基础上,综述和归纳了模式识别中采用的典型近邻性测度方法及其应用领域,阐明了近邻性与模式属性之间的关系以及在近邻性的度量中模式本身的特性与先验知识所起的重要作用.
模式识别;测度;度量;近邻性
0 引言
近邻性(proximity)是刻画事物间的差异或相似程度的量,差异程度可用距离来描述,而相似程度可用相似度来描述.近邻性的定量描述是模式识别中分类与聚类的基础,是所有以对象之间在某些特征上的相近程度为依据的信息处理问题中最为基本的问题.差异和相似性是从不同角度描述事物之间相近程度的量,二者之间存在对立关系:差异越大(小),相似性就越小(大),反之亦然.因此在很多的定性讨论中“近邻性”以广义的“相似性”来替代,而在本文中将严格区别相异性(dissimilarity)与相似性(similarity),并把二者统称为近邻性.
在机器学习、模式识别、数据挖掘等理论、方法和技术的研究中出现了大量的近邻性描述方法[1],其中离不开距离、近邻性、相似度等词汇.然而,很多情况下工程应用中的近邻性测度和度量并不一定都符合严格的数学定义,因而造成近邻性概念和使用方法上的混乱.本文以严格的数学定义为基础,首先介绍模式识别问题中常用的基本近邻性测度函数及其相关性质,分析不同方法的特点与适用问题;之后探讨近邻性与属性之间存在的内在关系以及先验知识在近邻性测度中的重要地位和相关的机器学习方法.
1 近邻性的本质
近邻性是事物及其存在形式与变化方式之间所拥有的共性,这种共性是系统的一个基本特征,是人们认知机制中的重要元素.系统科学认为这种共性体现在系统的结构和功能、存在方式和演化过程,是一种有差异的共性(等同是近邻的特例),是系统同一性的一种表现[2].不同领域中的近邻性具有同样的特性,如语言学中相似词语具有语义上的公共要素,代数学中相似矩阵具有相同的本征值,几何学中相似图形的对应边之间存在相同的比例关系,等等.学科内部、学科之间也存在相似性,因此,以已发现的科学规律为原型可以通过类比推理揭示新的科学规律;也可以从已有学科建立起另一学科,如认知科学就是在人脑的信息加工与计算机的数据处理之间的相似性基础上建立起来的[3].
近邻性与概念密切相关,其计算可以决定概念的发现[4].从对象与概念之间的关系上看,存在2种近邻性:一是对象与概念之间的近邻性,可用Zadeh的模糊隶属度来表示[5];二是在某概念下对象之间的近邻性,就是在特定概念下样本之间的近邻性.
概念的本质特征本身可以看作是相似性,因此在特定概念及其相关属性确定的前提下,合理定义近邻性的问题就是由相关特征提取本质属性的过程,一般属于监督学习(supervised learning)问题.但如果概念事先未知而只有给定的属性,那么近邻性对于概念的提取具有重要作用,这也是机器学习和模式识别的根本任务.
模式识别是以分类为基本目标的学科.分类(clasification)是以模式在特征空间中的近邻性为依据的,而聚类分析(clustering analysis)就是利用近邻性从有限数据中发现概念的技术和方法.机器学习从数据中提取任务相关的概念,其基本前提就是同属于1个概念的样例之间彼此相近.不同的近邻性测度隐含着对数据样本观察角度的不同,而这些角度都取决于函数自身的性质及其所表达的形状,倾向于发现适合于特定观察角度的不同形状的类结构[6].
2 近邻性的数学定义
近邻性描述事物及其存在和变化方式之间有差异的共性,其度量方法的基础是相异性测度和相似性测度,而距离和相似度是对相异性测度和相似性测度进行进一步限定而得出的函数.测度和度量是具有严格定义的数学概念,简单地说,测度是定义在集合子集上的实函数,而度量是评估集合中2个元素之间的差异或相似性的实函数.在近邻性程度的描述中,度量建立在测度之上.下面给出向量空间中点间的距离和相似度概念的基本定义和相关定理,这是构造更复杂的距离与相似度的基础.
定义1(相异性测度)[7-8]对向量集合X和实数集R,若函数d(d∶X×X→R)满足:①∃d0∈R s.t-∞ <d0≤d(x,y)<+∞,∀x,y∈X(下界存在性);②d(x,x)=d0,∀x∈X(自反性);③d(x,y)=d(y,x),∀x,y∈X(对称性);则称d为X上的1个相异性测度(dissimilarity measure,DM).
条件①规定了相异性测度存在一个确定的下界(存在“最近”的概念),条件②意味着任何向量与自身是最相近的,条件③规定了向量之间的相异性是2个向量之间相对而对等的概念.
定义2(距离)[7-8]如果向量集合X上的相异性测度d满足:④当且仅当x=y时,d(x,y)=d0(同一性);⑤d(x,z)≤d(x,y)+d(y,z),∀x,y,z∈X(三角不等式);则称d为相异性度量 (metric DM),又称距离函数,简称距离(distance).
作为距离函数的特性,条件④规定最近的2个向量必然是同一向量,反之亦然;条件⑤规定两点间直线距离最短.两点间的距离描述了它们所代表的模式之间的相异程度(dissimilarity level).由条件③—⑤可以导出距离函数的以下性质:
性质1(距离的非负性) 相异性度量是非负函数,即d0≥0.
定义3(超度量)[8-9]如果把距离函数d满足的条件⑤替换为更强的条件:d(x,z)≤max[d(x,y),d(y,z)],∀x,y,z∈X(强三角不等式),则函数d称为超度量 (ultrametric).
例如,离散度量
定义4(相似性测度)[7-8]对向量集合X和实数集R,若函数s∶X×X→R满足:⑥∃s0∈R s.t-∞ <s(x,y)≤s0<+∞,∀x,y∈X(上界存在性);⑦s(x,x)=s0,∀x∈X(自反性);⑧s(x,y)=s(y,x),∀x,y∈X(对称性);则称s为X上的1个相似性测度 (similarity measure,SM).
条件⑥规定了相似性测度存在1个确定的上界(存在“最相似”的概念),条件⑦意味着所有向量与自身是最相似的,条件⑧规定了向量之间的相似性是2个向量之间相对而对等的概念.
定义5(相似度)[7-8]如果向量集合X上的相似性测度s满足:⑨ 当且仅当x=y时,s(x,y)=s0(同一性);⑩s(x,y)s(y,z)≤ [s(x,y)+s(y,z)]s(x,z),∀x,y,z∈X(倒三角不等式);则称s为相似性度量 (metric SM),简称相似度(similarity).
上述条件⑨表示最相似的2个向量必然是同一向量,反之亦然;而条件⑩称为倒三角不等式是因为:当相似度s(x,y)>0,∀x,y∈X,且相异性与相似性的对立关系表现为反比关系时(相似度和距离并非一定存在反比关系),条件⑩等价于这与距离条件
⑤极其相似,只是测度值取了倒数.由条件⑧—⑩可证明相似度的以下2个性质:
性质1(相似度的保号性) 相似度一定是非负的:

或一定是非正的:

性质2(相似性的相容性) 非负相似度(式(1))中不存在与2个完全不相似(相似度为0)向量都相似(相似度大于0)的向量.
在模式识别的很多应用中取d0=0(向量到自身的距离定义为0),相似度常采用式(1),且s0=1(归一化)[8];然而一般情况下d0可能是其他正数,s0也可以取其他正数或负数(若采用式(2)).
距离和相似度是相互对立的,一般的基于空间距离d的相似度计算框架被认为是[4]:s=F(d),其中函数F(x)是x的非负递减函数,且0≤F(x)≤1,F(0)=1.从距离与相似度的基本定义出发可以证明以下结论成立(通过验证定义所要求的条件①—⑩来证明,而关键是验证条件⑤和⑩):
定理1(距离与相似度的反比转换) 若s为集合X上的相似度,且满足s(x,y)>0,∀x,y∈X,则d=a/s(a>0)是X上的距离;若d为集合X上的距离,且满足d(x,y)>0,∀x,y∈X,则s=a/d(a>0)是X上的相似度.
定理2(相异性与相似性的逆差转换) 若s为集合X上的相似性测度,则d=s0-s是X上的相异性测度;若d为集合X上的相异性测度,则s=dmax-d(dmax=maxx,y∈Xd(x,y))是X上的相似性测度.
通过对距离和相似度的适当函数变换可以导出新的距离和相似度函数.
定理3(距离和相似度的膨胀平移) 若d为集合X上的距离,则kd+a(∀a≥0,k>0)仍是X上的距离;若s为集合X上的相似度,满足s(x,y)≥0,∀x,y∈X,则ks+a(∀a≥0,k>0)仍是X上的相似度.
定理4(距离和相似度的函数变换) 若单调递增连续函数f∶R+→R+满足f(x)+f(y)≥f(x+y),∀x,y∈R+,而d为X上的距离,测度值下界为d0≥0,则f(d)仍为X上的距离;若单调递减连续函数g∶R+→R+满足g(x)+g(y)≥g(1/(1/x+1/y)),∀x,y∈R+,而s为X上的相似度,满足s(u,v)>0,∀u,v∈X,则g(s)仍为X上的相似度.
以点间的近邻性测度与度量为基础,可进一步定义点与集合、集合与集合之间的近邻性.在近邻性度量的很多应用中,定义中的条件不一定全部满足,但就特定的应用目的而言仍具有有效的使用价值.如果只有三角不等式不成立则称为半度量(semi-metric)[8].
3 基本的近邻性测度
在近邻性测度表述过程中,1个模式将会有3种表示方式:1)实向量空间中的特征向量x∈X⊆Rn,n表示向量维数,xk表示向量x的第k个分量;2)属性集合表示属性集合的元素个数;3)属性向量x∈{0,1}n,各维分量值为1或0,分别表示该模式中特定属性出现与否.对2个二值向量x,y∈{0,1}n,其各分量中0和1组合出现的可能性及其数量如表1所示.例如,b表示向量x和y同一维分量对(xk,yk)取(1,0)的数目.

表1 二值向量对的各维取值组合可能性表
3.1 相异性测度
在聚类分析等领域,Minkowski距离在刻画模式相异度的过程中起重要的作用[10].欧氏距离与现实空间距离概念一致而且常用于计算模式之间的空间位置差异;Manhattan距离是从1个点沿各坐标轴方向行进到达另1点的距离,在数字图像中2个像素之间的4邻接通路的长度就是这2个像素点间的Manhattan距离[11];Chebyshev距离是从1个点沿各坐标轴方向或45°方向到达另1点的距离,在数字图像中2个像素之间的8邻接通路的长度就是这2个像素点间的Chebyshev距离[11].
证明Minkowski距离为相异性度量的关键是证明定义2中的条件⑤,即Minkowski不等式:距离具有平移不变性,但只有p=2时(即欧氏距离)才具有旋转不变性[9].值得注意的是,Minkowski距离具有量纲,因此一定要采用相同量纲的变量.如果变量的量纲不同,测量值变化范围相差悬殊时,具有很大差异的属性将主导距离度量.因此首先要进行数据的标准化处理,然后再计算距离.Minkowski距离存在2个方面的问题:一是认为各分量的量纲(scale)因素均等;二是认为各分量的分布均等.实践中应尽可能地避免变量的多重相关性(multi-collinearity),因为多重相关性所造成的信息重叠,会片面强调某些属性的重要性.该性质对于最近邻规则算法的重要性表现在:最近邻算法的有效性会受到各维特征所选择的单位的影响,往往是单位选择较小的特征在欧氏距离的计算中起着较重要的作用,而单位较大的特征之间的差异在距离计算中往往被掩盖掉.为了解决这一问题,在分类之前可以分别对每个特征进行尺度变换,使得特征的尺度均衡化.具体实现时可以选择变换系数:其中max(xk)和min(xk)分别表示所有训练样本中第k维特征的最大值和最小值.

上述度量函数的定义中把特征向量的各维属性同等看待,为了表现不同属性的重要性差异,可以在度量函数的定义中为向量的各维指定不同权值,所得距离称为加权距离.加权Minkowski距离定义为:其中wk为第k个特征属性的权值,刻画该属性的重要程度.式(3)实际上就是一种权值.
当p不是1和∞时,Minkowski距离的计算代价是较大的.从解决问题和降低计算复杂度的需要出发,可以用其他距离函数逼近欧氏距离,如Chaudhuri等[12]提出了欧氏距离的1种逼近:dCha(x,y).这种逼近避免了欧氏距离计算中的平方和开方运算.上述距离也可用属性集合与属性向量表示,如欧氏距离的属性集合与属性向量分别表示为其中b,c的意义见表1.克服Minkowski距离依赖于量纲的1种改进距离就是Mahalanobis距离.
如果协方差矩阵为对角阵,则称为正规化的Mahalanobis距离:其中σk是样本第k维特征的标准差.这是把不同因素(如身高和体重)统一标准化处理的1种方法.
3)Canberra(Lance-Williams)距离这是1个无量纲的距离函数,但不能克服分量间的相关性.该距离的特点是向量间每个属性的差异利用这2个向量该属性之和进行规范化,每1项在[0,1]内取值:当2个向量的某一属性值相等时,相应的距离项为0;当2个向量某一属性值同号时,相应的距离项介于0和1之间;而一旦2个向量某一属性值异号时,相应的距离项变为1;距离值最终取值于[0,n].该距离常用于图像特征差异的分析等应用中[16].
对二值向量x,y∈{0,1}n来说,Hamming距离就是二者的异或运算结果中1出现的个数,也等于向量间的Manhattan距离容易证明,二值离散空间中向量间的欧氏距离就是这2个向量之间Hamming距离的平方根1}n为属性向量,则有Hamming距离的另一有意义的表述:其中b和c的含义见表1.用属性集合表示模式时,2个模式A和B之间的Hamming距离就是2个集合中相异元素的个数:
Hamming距离在信息论、通信、计算机技术等领域的应用非常广泛[17].在编码过程中为了检测e个错误,需要1个Hamming距离为e+1的编码方案,而为了纠正f个错误,需要1个距离为2f+1的编码方案.在聚类分析的应用中,Hamming距离仍是简洁有效的相异性度量[18],在本文相似度计算等其他领域,Hamming距离也得到了广泛的应用[19].
5)Tanimoto距离.用属性集合表示模式时,模式A和B之间的Tanomoto距离定义为属性向量x,y∈{0,1}n之间的Tanimoto距离定义为其中a,b,c的含义见表1.Tanimoto距离的意义为:2个向量所代表的模式非共享属性个数占共同拥有属性个数的比例,即2个模式组成结构的差异.
Tanimoto距离符合相异性度量的全部要求[20],取值于[0,1]:当2个集合互不相交(具有完全不同属性)时取最大值,当2个集合相等(具有完全相同属性)时取最小值.Tanimoto距离广泛用于分类学和刻画结构之间的差异[21-22],也可以用于表示文档数据的差异.
3.2 相似性测度
以下给出的相似性函数都是相似性测度,但不是相似性度量,因为它们不满足相似性度量的条件⑩.根据定理1和2,相似性与相异性测度是可以相互转换的,对任何1个相似性测度s,都可以构造相应的相异性测度d.以下相似性测度通常采用定理2转换为相异性测度,然而所得到的相异性测度不一定是相异性度量.

3)Tanimoto测 度 (Tanimoto系 数,Jaccard系 数当模式类X中的向量归一化为长度为a>0的等长向量时,该测度可改写为:sTan(x,y)测度是余弦测度的推广,显然具有旋转不变性,其取值范围是[-1/3,+1],在x=-y时达到最小值,在x=y时达到最大值,而当2个向量正交时测度值为0.
用属性集合表示模式时,模式A和B之间的Tanomoto测度定义为:值域为[0,1].属性向量x,y∈ {0,1}n之间的Tanimoto测度定义为:

值域也是[0,1].由此可见,Tanimoto测度是共享属性个数占共拥属性个数的比例.Tanimoto测度常用于计算样本集之间或模式结构之间的相似度[26],也可以用来计算字符串之间的相似性、对象集合之间的匹配度等测度.在聚类算法研究中,Tanimoto测度应用于聚类有效性假设检验的外部准则中[7].

取值范围皆为[0,1].Dice测度与Tonimoto测度都用于计算模式或对象集合之间的相似程度,但不完全相同,主要区别是:①由Tanimoto测度构造的Tanimoto相异性测度是距离函数,但按构造的Dice相异性测度不是1个度量.②比较(5)和(6)式可知,这2个测度对非共享属性(不相交集合元素)个数的权重不同,Tanimoto测度考虑总体属性个数时对共享和非共享属性均等看待,而Dice测度则降低非共享属性个数的作用(仅考虑半数);因此,在共享属性个数相同的情况下,Tanimoto测度值往往比Dice测度值小,是较为悲观的评估.
除此之外,在具体应用中还可以定义很多不同的相似性测度,如文献[27]为研究流式细胞计数数据的实时自适应聚类问题,采用了相似性测度
3.3 动态相似性测度
在语音识别、生物信息学、信息检索、机器翻译、辞典编撰和方言学等领域,需要度量字符串之间的相似性.因为字符串长度不固定,无法用前述的近邻性测度去衡量字符串之间的差异或相似性.这种情况下,可以使用动态近邻性测度,典型的描述方法是采用Levenshtein距离(编辑距离).
在文本信息检索、剽窃抄袭检测等领域文本近邻性的度量是基础性问题[29],而编辑距离是自然语言文本近邻性度量中的重要方法,文本字符串的距离越大,说明它们的差异越大.编辑距离通常用于句子的快速模糊匹配领域,但其规定的编辑操作不够灵活,也没有考虑语句的同义替换.编辑距离的计算需要通过特定的算法实现[6,8,30],动态规划是常采用的方法.基于编辑距离可以定义字符串之间的Levenstein相似度
3.4 半度量和超度量
定理3和定理4表明距离函数的特定函数变换仍然是距离函数,但并不是所有形式的函数变换都可以得到新的度量,即使这种变换会带来应用中的好处.例如:欧氏距离是距离函数,然而欧氏距离的平方却不是.半度量不满足三角不等式,因此两点之间直线半度量距离不一定最短(见图1).因此,半度量距离(准确地说是“相异性半度量”)在反映相异性程度的意义上有使用价值(距离越大差异越大),但距离之间的运算结果不一定会提供有意义的结果(半度量距离的部分之和并不等于整体).
平方欧氏距离dsEqcru(x,y)= (x-y)T(x-y)就是1个半度量距离.该距离可提供两点间空间距离的长短大小的信息,因不必进行开方运算可降低计算复杂度.使用中可以通过比较平方欧氏距离来判定2个长度的大小,然而不能通过2个平方欧氏距离之和计算2个线段的长度之和.
基于合并的层次聚类中如果把合并2个模式所需要的最短步数定义为这2个模式之间的距离,可得到超距离度量.因为类之间的距离的排序能够得到严格保持,所以基于超度量的聚类准则不易导致局部最小[9].

图1 3个向量之差的欧氏范数的关系

3.5 模糊相似性测度
考虑实向量x,y,它们的分量xk,yk∈ [0,1](i=1,2,…,n),这些分量的值表示拥有第k个属性的可能程度.如果x拥有(或不拥有)第k个属性的可能性越大,则xk接近于1(或0);如果xk接近于1/2,则x是否拥有第k个属性的不确定性最大.这种向量称为模糊向量,其分量是模糊逻辑中的隶属度[5].2个实值变量xk,yk∈[0,1]的模糊相似性测度可定义为sFuz(xk,yk)=max[min(1-xk,1-yk),min(xk,yk)],该测度值取值于[0,1].基于变量之间的相似性测度,可以定义2个向量x,y之间的通用相似性测度[7该测度值取值于[0,n1/q],若2个向量所有对应维分量值中1个为0(1)时另1个为1(0),即2个向量的属性组清晰而相斥,则该函数值为0;当2个向量所有对应维分量值彼此相等且皆为0或1,即属性组清晰而一致,则该函数值为n1/q.同一向量间的相似性测度值满足的每个分量为1/2时达到最小值,x的每个分量为0或1时达到最大值.由此可知,该函数不满足测度定义中的自反性条件,因此严格来说不是测度.
从上述定义可以得出如下结论:①模糊向量是模糊概念的一种表示,向量间的相似程度不仅取决于相互间的相近程度,同时还取决于向量表示概念的清晰程度,即使是相同的向量,如果不是对概念的清晰表示,相似程度不会达到最大;②当2个向量都是对概念的清晰表示时,二者之间的相似程度可以达到0(最小)或1(最大);③同一向量间的模糊相似性测度不会低于最大值的1/2,即向量与自身相似的程度至少要达到50%.
3.6 相似性融合
如何将相似性进行有效融合是相似性研究面临的重要难题[4].当2个样例同时具有连续属性和离散属性,甚至某些属性缺失时,需要将2个不同近邻性计算融合,常用方法是Gower模型[31]:sGow(i,j)其中sk(i,j)是第i个样本和第j个样本在第k个属性上的相似性;wijk是属性权值,通常的取法是当第k个属性缺失时为0,否则为1.
4 近邻性与属性
丑小鸭定律说明,世界上所有事物之间的近邻性都是一样的,丑小鸭与天鹅之间的差别与2只天鹅之间的差别一样大[32].因此,不存在“纯客观”的分类准则,人们进行分类所依据的一切准则都是主观的,而选择什么准则进行分类则纯属主观评价问题,是一个涉及到价值观的问题.分类准则的不同源于分类目的的不同,因而选择特征时所持的价值观也不同[33].而分类准则直接依赖于近邻性的度量方法,这意味着属性选择的不同,或者对不同属性所赋予的重要性不同,近邻性度量的结果也会不同.例如,以体长为特征时马和牛比起马和小汽车更相近,但以奔跑速度为特征时马和小汽车更相近.
在许多模式识别问题中,特征向量的各分量常常代表不同的物理量(如颜色和长度),不具有可比性.“如何处理各分量代表不同物理意义的向量”,这一问题没有可通用的方法来解决.在实践中,选择1个相似函数或对数据进行某种规格化,就意味着设计者引入了额外的信息用来赋予这种操作以明确的物理意义[9].
对数据进行规格化处理是使数据处理对坐标系变换具有不变性的一种方法.这种方法的出发点是防止某些特征仅仅因为其数值过大而主导距离的度量.然而,如果数据的波动是因为存在多个类,那么这种规格化反而会导致不真实的数据分布结构[9].因此,对问题本身的深入分析总是模式识别的首要任务和解决问题的根本基础.
5 结论
模式识别中典型的和常用的基本近邻性测度及其应用见表2.由于篇幅所限,本文不可能介绍全部近邻性测度函数,而有些未涉及到的函数也是很重要的,如2个概率分布P(x)和Q(x)之间的差异性测度——Kullback-Leibler距离(相对熵,信息偏差该函数在信息论中具有重要地位[17],同时也应用于说话人检索等领域[34].另外,在聚类分析中,为了把1个模式对象归类为某一类别以及为了合并最相似的2个类,需要计算模式对象与类别(模式对象的集合)之间的近邻性和2个集合之间的近邻性测度.集合之间的近邻性测度问题还出现在诸如图像相似性的计算等过程中[7,15],其中典型的有Hausdorff距离.
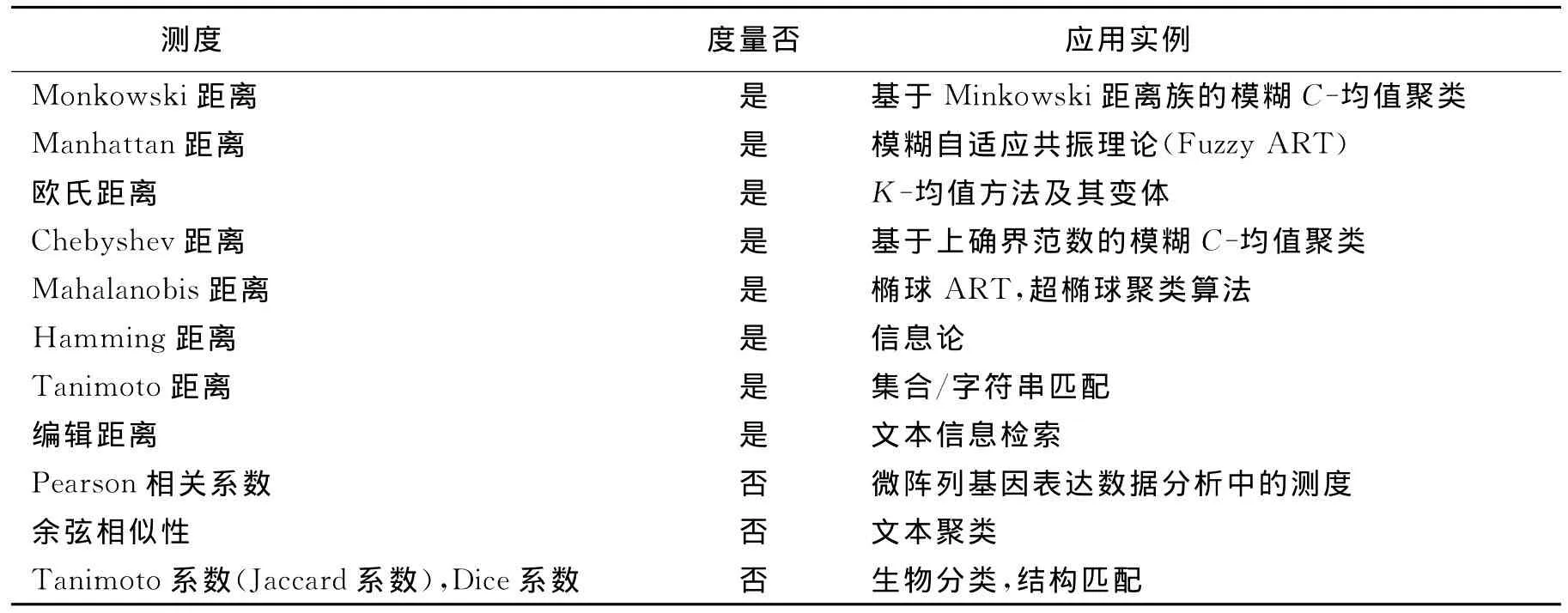
表2 近邻性测度与应用
本文所介绍的相似性测度都不是相似性度量,而且关于相似度(similarity)在一些文献中并未要求倒三角不等式.大多数情况下,相似性的描述是通过相似系数(similarity coefficient)来实现的[35],而相似系数sij定义的核心是[36]∶-1≤sij≤1,sij≤sii=1,sij=sji.关于距离和相似系数的完整的讨论与专门应用可参见文献[28].
与相似性测度相比,距离函数更注重解释对象之间的差异;从描述对象的属性角度来说,距离函数能更有效地表征2个对象共同缺少的属性.对于连续变量,迄今欧氏距离仍为应用最广泛的1种方法.然而,近邻性测度函数并不是脱离人的主观世界而存在的客体,其构造形式隐含了人们解决特定问题的目的性,某一测度函数仅适应于解决特定的1类问题.如何利用分类信息或者类别的其他先验信息来研究近邻性是有监督的近邻性研究.通过训练数据集学习1个能够很好地反映样本空间特性的距离函数作为目标的机器学习方法称为度量学习[37].
在近邻性研究领域当前人们关注的主要问题为[4]:①如何将先验知识引入到相似性计算中;②如何构建完善的相似性融合模型;③如何选择相似性模型中的参数.
模式识别的研究对象是客观的,而认识客观对象及其存在与演化方式是人的事情,近邻性的计算方法是人们对客观世界的认识过程,与认识问题与解决问题的目的性紧密相关.相异/相似性作为主体对客体的1种认定手段,始终要在特定目标约束下揭示客体及其存在与演变的真实规律,模式本身的特性和对它的先验知识必须体现在近邻性测度中.
[1] Cha S H.Comprehensive survey on distance/similarity measure between probability density functions[J].International Journal of Mathematical Models and Methoeds in Applied Sciences,2007,1(4):300-307.
[2] 魏宏森,曾国屏.系统论:系统科学哲学[M].北京:清华大学出版社,1995:276.
[3] 史忠植.智能科学[M].北京:清华大学出版社,2006:315.
[4] 于剑.概念、相似性与聚类分析[C]//周志华,杨强.机器学习及其应用2011[M].北京:清华大学出版社,2011:136-146.
[5] Zadeh L A.Fuzzy sets[J].Information and Control,1965,8(3):338-353.
[6] Pedrycz W.Clustering and fuzzy clustering[C]//Pedrycz W.Knowledge-based clustering:from data to information granules[M].John Wiley &Sons,2005.
[7] Theodoridis S,Koutroumbas K.Pattern recognition[M].4th ed.Elsevier,2009:602-625.
[8] Xu R,Wunsch II D C.Clustering[M].John Wiley &Sons,2009:15-30.
[9] Duda R O.Pattern classification[M].2nd ed.John Wiley &Sons,2001.
[10] de Amorim R C,Mirkin B.Minkowski metric,feature weighting and anomalous cluster initializing in K-Means clustering[J].Pattern Recognition,2012,45(3):1061-1075.
[11] Gonzalez R C,Woods R E.Digital image processing[M].2nd ed.USA:Prentice-Hall,2002.
[12] Chaudhuri D,Murthy C A,Chaudhuri B B.A modified metric to compute distance[J].Pattern Recognition,1992,25(7):667-677.
[13] 张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004:225-227.
[14] Xiang S,Nie F,Zhang C S.Learning a mahalanobis distance metric for data clustering a classification[J].Pattern Recognition,2008,41(12):3600-3612.
[15] Wang L,Zhang Y,Feng J.On the euclidean eistance of images[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(8):1334-1339.
[16] Kokare M,Biswas P K,Chatterji B N.Texture image retrieval using rotated wavelet filters[J].Pattern Recognition Letters,2007,28(10):1240-1249.
[17] Cover T M,Thomas J A.Elements of information theory[M].John Wiley &Sons,1991:209-212.
[18] 李彬,汪天飞,刘才铭,等.基于相对Hamming距离的Web聚类算法[J].计算机应用,2011,31(5):1387-1390.
[19] 张焕炯,王国胜,钟义信.基于汉明距离的文本相似度计算[J].计算机工程与应用,2001,37(19):21-22.
[20] Lipkus A H.A proof of the triangle inequality for the tanimoto distance[J].Journal of Mathematical Chemistry,1999,26(1-3):263-265.
[21] Tanimoto T.An elementary mathematical theory of classification and prediction[M].New York:International Business Machines Co.,1958.
[22] Jarvis R A,Patrick E A.Clustering using a similarity measure based on shared near neighbors[J].IEEE Transactions on Computers,1973,C-22(11):1025-1034.
[23] Ricardo B Y,Berthier R N.Modern information retrieval[M].New York:ACM Press,1999:26-29.
[24] Tan P N,Steinbach M,Kumar V.Introduction to data mining[M].Addison-Wesley,2005:500.
[25] Eisen M B,Spellman P T,Brown P O,et al.Cluster analysis and display of genome-wide expression patterns[C].Proc Natl Acad Sci USA,1998,95:14863-14868.
[26] 汤燕彬,许榕生.基于Tanimoto系数的JPEG碎片数据识别方法[J].计算机应用与软件,2011,28(9):80-81;92.
[27] Fu L,Yang M,Braylan R,et al.Real-time adaptive clustering of flow cytometric data[J].Pattern Recognition,
1993,26(2):365-373.
[28] Deza E,Deza M M.Dictionary of distances[M].Elsevier,2006.
[29] 邓爱萍,徐国梁,肖奔.程序源代码剽窃检测串匹配算法的研究[J].计算机工程与科学,2008,30(3):62-68.
[30] 邹旭楷.汉字/字符串编辑距离和编辑路径的有效求解技术[J].计算机研究与发展,1996,33(8):574-580.
[31] Gower J C.A general coefficient of similarity and some of its properties[J].Biometrics,1971,27(4):857-871.
[32] Watanabe S.Knowing and guessing:a quantitative study of inference and information[M].New York:Wiley,1969:376-377.
[33] 赵南元.认知科学揭秘:认识科学与广义进化论[M].2版.北京:清华大学出版社,2002:8-9.
[34] 韩纪庆,郑铁然,郑贵滨.音频检索理论与技术[M].北京:科学出版社,2011:194-195.
[35] Sesli1 M,Yegenoglu E D.Comparison of similarity coefficients used for cluster analysis based on RAPD markers in wild olives[J].Genetics and Molecular Research,2010,9(4):2248-2253.
[36] Tomas M S,Alsina C,Rubio-Martinez J.Pseudometrics from three-positive semidefinite similarities[J].Fuzzy Sets and Systems,2006,157(17):2347-2355.
[37] Yang L,Jin R.Distance metric learning:a comprehensive survey[EB/OL].Michigan:Michigan State University,2006.http://www.cse.msu.edu/~rongjin/semisupervised/dist-metric-survey.pdf.
Proximity measures in pattern recognition
CUI Rong-yi
(Intelligent Information Processing Lab.,Dept.of Computer Science &Technology,College of Engineering,Yanbian University,Yanji 133002,China)
The quantitative description of dissimilarity and similarity between patterns is a basic problem in pattern recognition.On the basis of exposition and discussion on the essence and mathematical definition of proximity,the typical proximity measures and their applications are summarized.Furthermore,the relation between proximity and attributes of pattern,and the important roles of the features of patterns and a priori knowledge are pointed out.
pattern recognition;measure;metric;proximity
TP391.4
A
1004-4353(2012)03-0236-11
20120712
崔荣一(1962—),男,博士,教授,研究方向为模式识别、智能计算.

