基于多元气温概率模型的气象保险的定价和风险评估

金哲值

（延边大学理学院 数学系，吉林 延吉133002）

基于多元气温概率模型的气象保险的定价和风险评估

金哲值

（延边大学理学院 数学系，吉林 延吉133002）

为了提高日常气象风险管理的必要性和改善气象保险高保费导致市场活跃度低的现状，相对于仅反映日值气温变化的标准Cao－Wei模型，提出了反映气候变暖趋势以及各地域间关联的新的多元气温概率模型．利用多元气温概率模型对气象保险进行了定价，并对气象保险风险的地域组合进行了风险分散效果的评价．关键词：多元气温概率模型；Cao－Wei模型；气象保险

目前，现行气象保险的价格高于所支出的平均保险金额，其主要原因在于气象变量的不确定性，同时也与拟定保费模型的可行性较低有直接关系．当前保险公司普遍采用的方法是利用过去已知的气象变量的经验分布或者使用较为简单的气温概率模型［1－2］，由于这些方法难以反映气候变暖的趋势和各地域之间的相关关系，因此需要建立能够充分反映气象变量特征的模型，以拟定适当的保费．为此，本文提出了1种能够反映气候变暖趋势和各地域间相关关系的多元气温概率模型．气象保险的各地域保费以“纯保费＋k×标准差”的形态产生．如果多个地域出售气象保险并形成风险地域组合，便可通过风险分散的效果使综合风险低于各地域风险的单纯叠加之和．如果模型能很好地反映出这种风险分散效果，便可以改善气象保险高保费引起的市场活跃度较低的现状．为了尝试激活气象保险市场，以担保夏季异常低温现象的气象保险为例，提出了1个用来改善气象保险定价的新模型，通过基于多元气温概率模型的蒙特卡洛模拟方法对气象保险进行了定价，并验证了气象保险地域组合的风险分散效果的可行性．

1 多元气温概率模型

1．1 先行研究的气温概率模型

Cao－Wei［1－2］和Changsoo Lee［3］的研究中，在反映特定地域的气温季节性和周期循环性等特性的条件下，将误差项假定为AR（1）模型，以便反映该地域日值气温的自相关性．Changsoo Lee对Cao－Wei模型做了如下的修正：

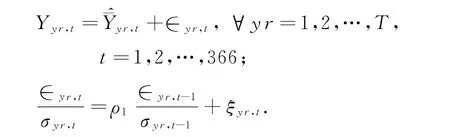
1．2 基于可变量时间序列回归模型的气温概率模型（单元模型）

气温数据拥有明显的季节性和周期循环性等特性，但因先行研究的气温概率模型把这种特性包含在误差项里，所以对未来气温的预测只能简单地由过去日值平均气温和变暖趋势来决定．可变量时间序列回归模型对时间序列数据，如有1个固定季节变化的情况非常适合．若在气温概率模型中利用可变量时间序列回归模型来预测未来气温，它不仅可以包含固定的季节性变化，又比现有模型更能准确地反映出气温的变化趋势．下述模型是把特定地域气温用日值变量Xm，d和特定年度特定月份相对应的可变量Dyr，m来表示的线性回归模型．日值变量Xm，d的效果是对应日温度与基准日（1月1日）温度差异的平均值的效果．特定年度特定月份可变量Dyr，m的效果是与基准年（1980年）的特定月份与其他年度特定月份之间的气温差异．

用以下模型表示多个地域残差的日标准差，即反映日值气温的异方差性．

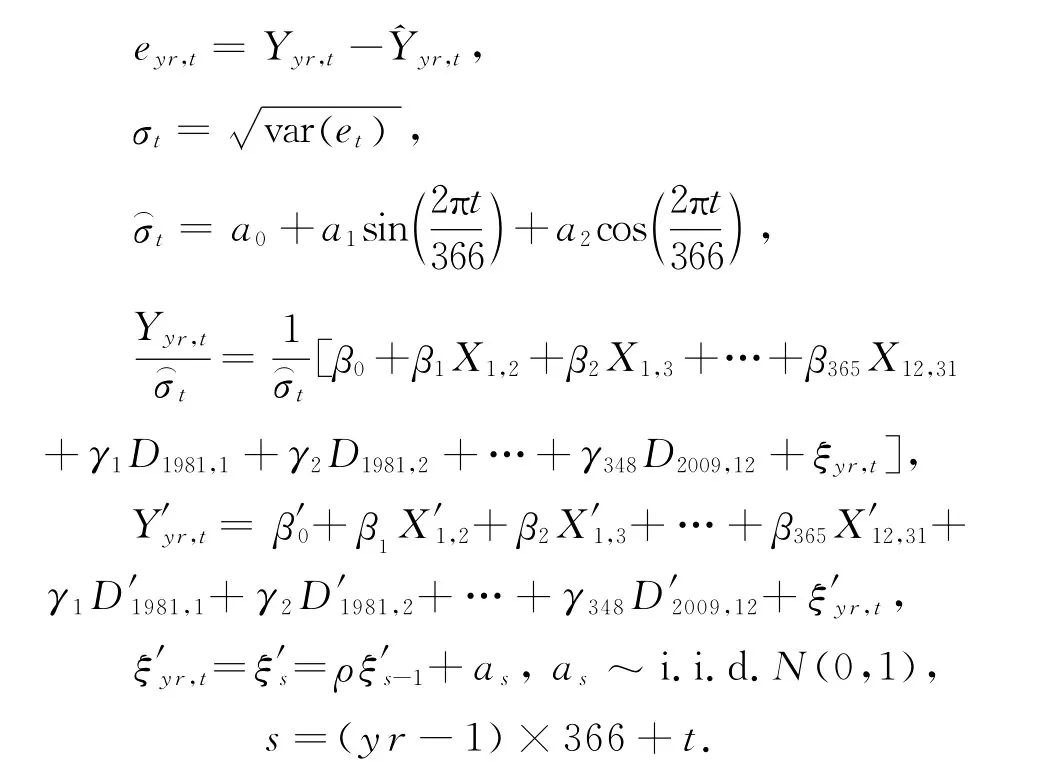
虽然上述模型能够反映每月全球变暖的趋势，但不能预测未来的气温．为了能达到预测未来气温的要求，故对全球变暖趋势部分做修改得到如下回归模型：

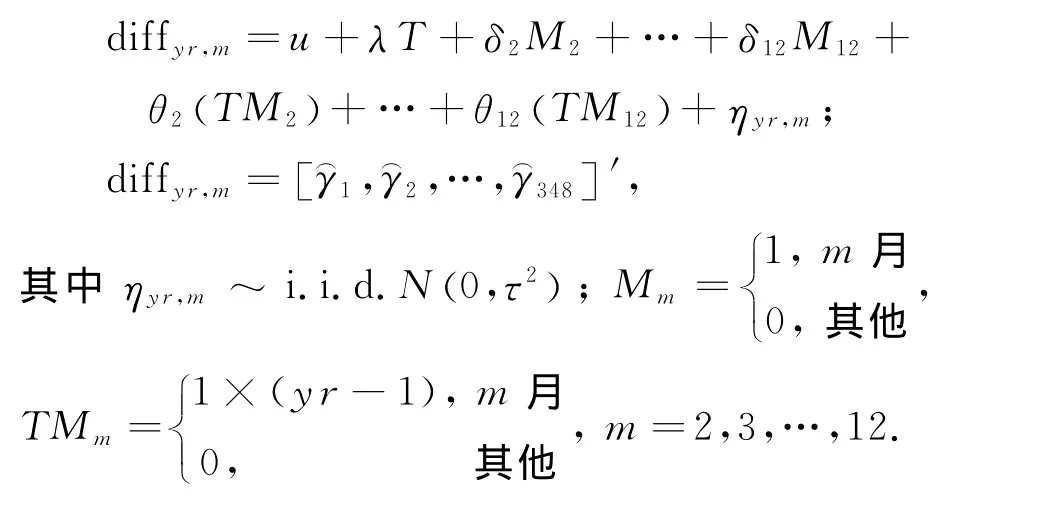
模型估计的特定年度的每月的影响（γ^1，γ^2，…，γ^348）用因变量diffyr，m表示，自变量用每年趋势T、每月可变量Mm、每年趋势和特定月的交替变量TMm的线性回归模型拟合．上述回归式的参数估计结果表明，每月的影响和交替变量的影响基本不存在．为了使回归模型更符合未来的场景，以全球变暖趋势的变量替换每年趋势变量T，并重复前2个过程后最终得到如下单一地域的气温概率模型：

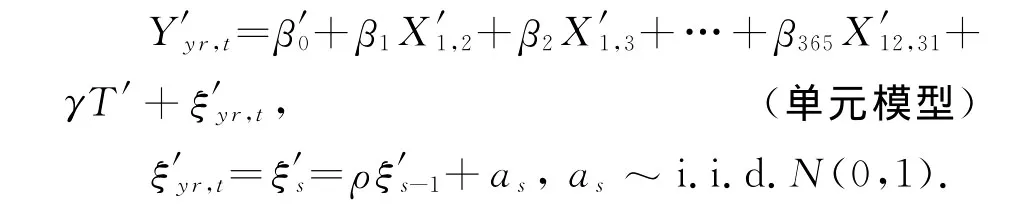
1．3 基于多元时间序列模型的气温概率模型（多元模型）

在上述修正模型上添加表示各不同地域的可变量和交互变量（同时反映地域和日值效果的可变量RrMm，d），便能够反映出不同地域的气温效果．多元时间序列模型具体表达式为：

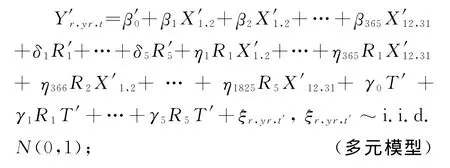
表1是通过上述模型得到的各地域间残差的相关关系．由于上式不能明确地表示出各地域间的相关关系，所以需要建立1个能表现出残差结构的模型．下式是利用多元时间序列模型VAR（1）（Vector Autoregressive 1 Models）对残差所进行的建模，它可估计地域间的相关关系和自相关性．

表1 地域间气温变化残差的相关系数（时差＝0）℃

为了验证模型对数据的拟合度，选取检验统计量RMSE（Root Mean Squared Error），其值越小对数据的模型拟合度越高．具体验证结果参见表2和图1，其中检验统计量的表达式为：RMSE＝，其中n＝年度数×t，k＝自由度．由表2和图1中RMSE的比较结果可看出，多元气温概率模型在对数据的拟合度以及预测将来气温等方面比现有的模型更优越．该多元气温概率模型不仅在气象保险定价和风险评估方面优于现有的模型，而且在降低气象保险费用方面也能起到良好的效果．

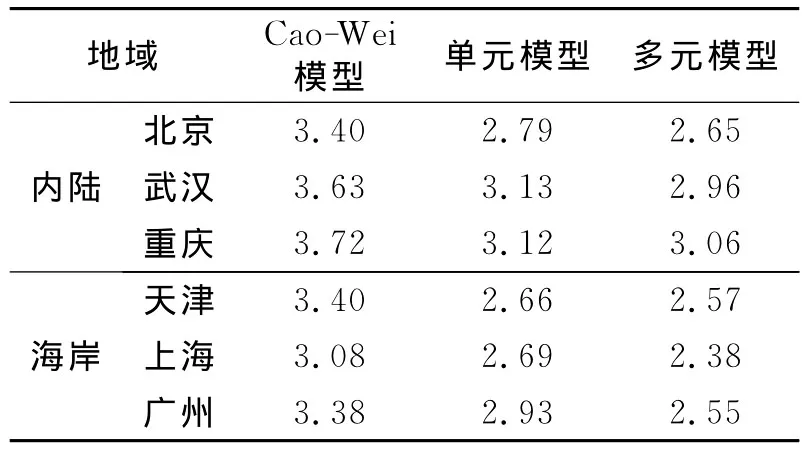
表2 模型拟合度比较（以RMSE为基准）

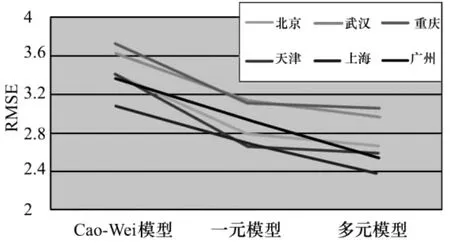
图1 反映6个地域的模型的RMSE比较

2 基于气温概率模型的气象保险定价

2．1 气象保险的设计

Changsoo Lee［3］模型对所有城市设定了相同的担保基准，但本文考虑到各地域过往特征（基础统计量）等因素后，设定了新的担保内容．表3是在考虑日值平均温度的均值和标准差之后确定的气象保险的担保内容．

2．2 气象保险的定价

本文所使用的定价方法采用了对将来预测的所有气温场景所支出的保险金的平均金额再加上安全增值的毛保费计算方式，即通过蒙特卡洛模拟所生成的各场景中低于基准温度的日数按地域分别计算得出，其中超过35 d的日数平均值设为纯保费．考虑到将来可能产生的巨大损失，把超过日数1倍的标准差设为安全增值来计算毛保费．表4为通过多元气温概率模型计算出的各地域保费．与Changsoo Lee［3］模型相比，保费的安全增值部分减少了很多，即通过多元气温概率模型可以计算出比现有保险费更低的保费．但到目前为止，安全增值仍然占据着保费中80%以上的比例，所以有必要进一步探讨地域气象保险风险、地域组合的管理和风险分散效果对气象保险带来的影响．

表3 气象保险的内容设计

表4 通过模拟实验计算的保险费 亿元

3 气象保险地域组合的风险评估

通过多元气温概率模型，在各地域销量不同的条件下，可对风险地域组合损失分布的变化做出研究，并且可分析出损失分布的风险分散效果对降低保费所带来的影响．

3．1 气象保险地域组合的风险评估

把计算得出的各地域的毛保费应用到各个场景，可得如表5所示的各地域的损失分布．

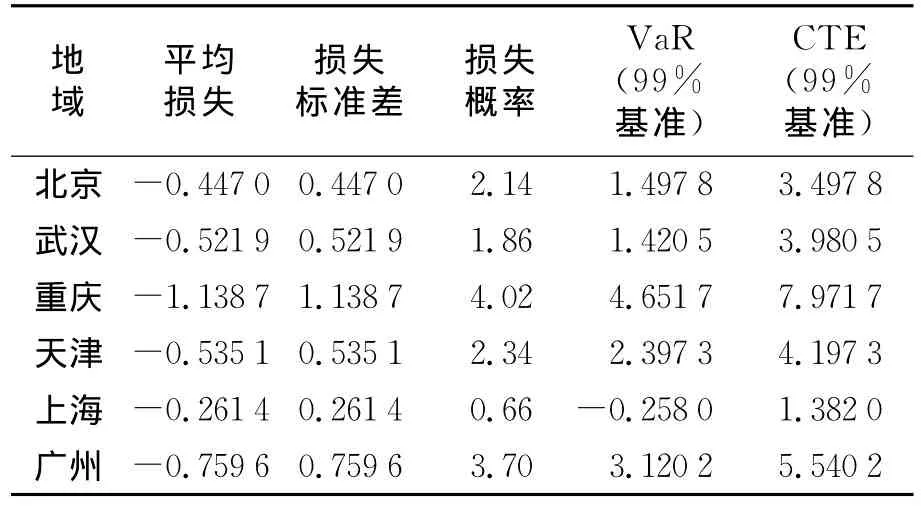
表5 通过模拟实验进行损失风险的评价亿元，%

但须注意的是，如果各地域气象保险销量相同，则不适合利用上面的结果评价保险公司的风险．本文对各地域间简单叠加的损失统计量和地域组合的损失统计量做了比较，并估计了毛保费降低率，见表6和图2．

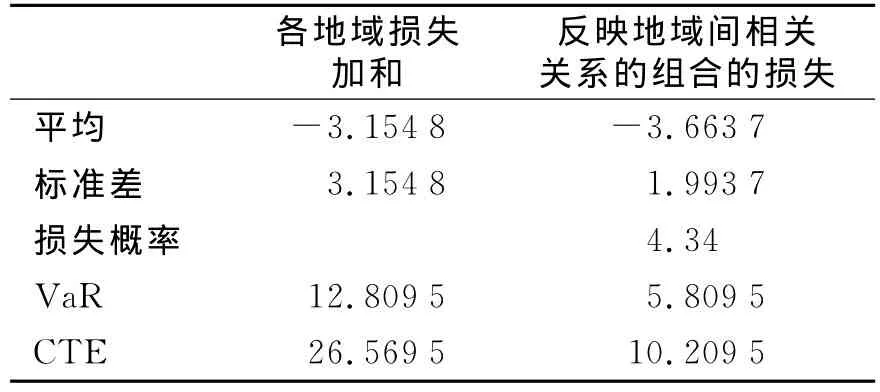
表6 气象保险地域组合的损失分布e．g．1亿元，%

图2 地域组合的损失分布

3．2 考虑各地域销量情况下的地域组合风险评价

为了评估各地域气象保险的销量，需对各地域气象保险的需求做事先调查．本文只是单纯地假定各地域销量受到该地域经济规模的影响，并以各地域内的生产总值（GRDP）所占的百分比作为比重来评估风险．表7给出了各地区GRDP的比重．表8和图3是反映地域内比重的简单相加与表5的损失统计量的比较结果．通过反映各地域间的相关关系，标准差减少了45．4%，从而进一步明确了气象保险地域组合的风险分散效果的有效性．

表7 反映各地域保险销量的基准百万元，%

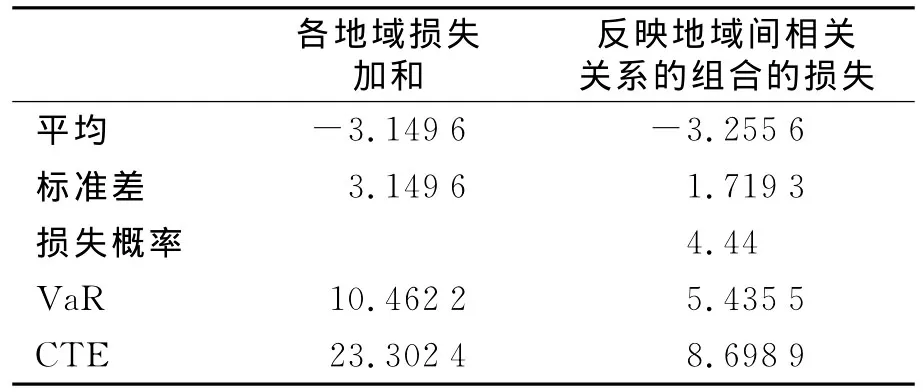
表8 参考各地域销量比重因素后地域组合的损失分布e．g．1亿元，%

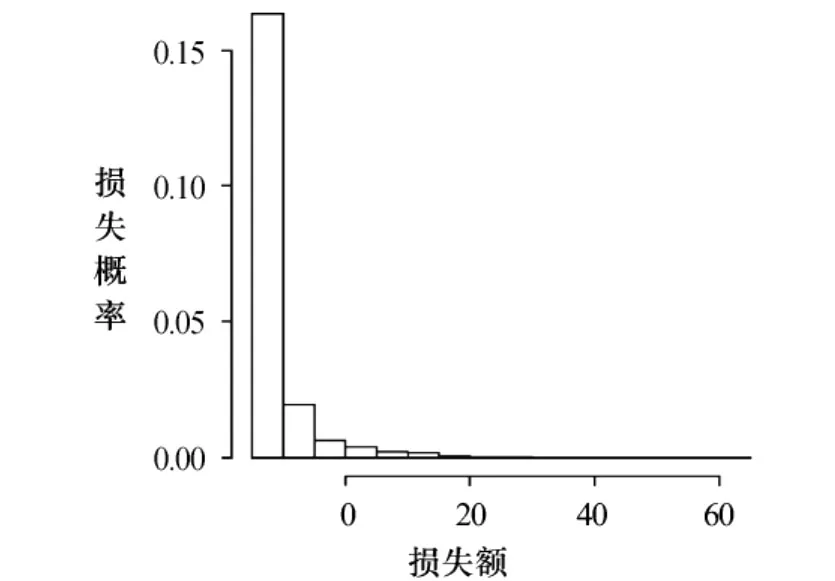
图3 反映比重后的地域组合的损失分布

4 结论

本文首先提出适用于日值气温变化、反映气候变暖趋势以及不同地域间关联的多元气温概率模型，然后设定了新的以夏季异常低温现象为担保内容的气象保险，并利用多元气温概率模型做出了精确的定价，并在此基础上，验证了气象保险地域组合的风险分散效果的有效性．结果表明：这种风险分散效果不仅改善了模型的拟合度，而且在降低保险价格方面也起到了非常重要的作用．

［1］ Cao M，Wei J．Pricing the weather［J］．Risk，2000：67－70．

［2］ Cao M，Wei J．Weather derivatives valuation and market price of weather risk［J］．The Journal of Futures Markets，2004，24（11）：1065－1089．

［3］ 李昌洙，河弘俊．基于气温概率模型对气象保险定价的研究［J］．保险开发研究，2008，19（2）：55－76．

［4］ Dornier F，Queruel M．Weather derivatives pricing：caution to the wind［J］．Risk，2000：30－32．

［5］ Hull J C，White A．Pricing interest rate derivative securities［J］．Review of Financial Studies，1990，3（4）：573－592．

［6］ Shimko D．The valuation of multiple claim insurance contracts［J］．Journal of Financial and Quantitative Analysis，1992，27（2）：229－246．

［7］ 权元太．气候变化的科学现状与前景［J］．韩国气象学会学报，2005，41（2/1）：217－337．

Pricing and risk evaluation of weather insurance based on multivariate temperature model

JIN Zhe－zhi
（Department of Mathematics，College of Science，Yanbian University，Yanji 133002，China）

In order to improve the necessity of the management of the everyday weather risks and to make the circumstances of the low market activities that caused by high premium of weather insurances better，a multivariate temperature model，which reflects global warming trend and correlation of geographical regions is proposed compare to the Cao－Wei model which is the standard model that reflects the daily temperature change．Weather insurance pricing and effect evaluation for the risk spreading of the geographical combination of the risks of weather insurances are made by the multivariate temperature model．

stochastic multivariate temperature model；Cao－wei model；weather insurance

F840．6

A

1004－4353（2012）03－0191－05

20120803

金哲值（1977—），男，博士，讲师，研究方向为信息统计与保险精算．