基于光纤连接的腔系统实现两比特离散量子傅立叶变换
张英俏
(延边大学理学院 物理系,吉林 延吉133002)
基于光纤连接的腔系统实现两比特离散量子傅立叶变换
张英俏
(延边大学理学院 物理系,吉林 延吉133002)
提出了在外加经典场驱动的情况下,利用光纤连接的2个腔系统执行两比特离散量子傅立叶变换的方案.该方案通过发送2个原子交替通过一系列经典场和腔场来实现,而且该两比特方案可推广至N比特离散量子傅立叶变换.
离散量子傅立叶变换;腔QED;光纤
0 引言
离散量子傅立叶变换(DQFT)作为一种重要的量子算法,可表示为下面的线性幺正变换

其中|j〉=|j1j2…jn〉是1个给定的n比特态,且有ji∈ {0,1},0.jljl+1…jm=jl/2+jl+1/4+… +jm/2m-l+1.近几年,研究者已经提出了许多执行离散量子傅立叶变换的方案,其中包括利用选定原子依次通过一系列经典场和高Q腔执行离散量子傅立叶变换的方案[1].此后,又有几个利用腔量子电动力学执行离散量子傅立叶变换的可选方案被提出,这些方案中有的是通过设计可调节的两比特条件相位门[2],有的是通过使用两比特受控非门和SWCZ门[3],有的是利用一步CRkS门代替复杂的受控Rk门和SWAP门操作[4].此外,核磁共振系统[5]和光学系统[6-7]也被用于实现离散量子傅立叶变换.目前,虽然在实现离散量子傅立叶变换方面取得了大量进展,但在实际实验中仍存在许多问题.本文提出1个利用2个由光纤连接的腔系统执行两比特离散量子傅立叶变换的方案.
1 原子-腔光-纤相互作用
考虑2个全同原子处于2个由光纤连接的腔中,每个原子有1个激发态|r〉j和2个基态|e〉j和|g〉j.|e〉j→|r〉j跃迁由拉比频率为Ω的经典场驱动,其失谐量为Δ.|g〉j→|r〉j跃迁由腔模耦合,其耦合常数为g,失谐量为~Δ.该系统的相互作用哈密顿为

其中aj和aj†分别是第j个腔模的消灭算符和产生算符.在Δ,~Δ≫Ω,g的条件下,激发态|r〉j能够被绝热消除掉,因此HI可写成


其中b和b†分别是光纤模的消灭和产生算符,υ是光纤与腔模的耦合常数.
定义3个玻色子模[9]:

描述原子 -腔耦合和腔 -光纤耦合的哈密顿可分别改写为:
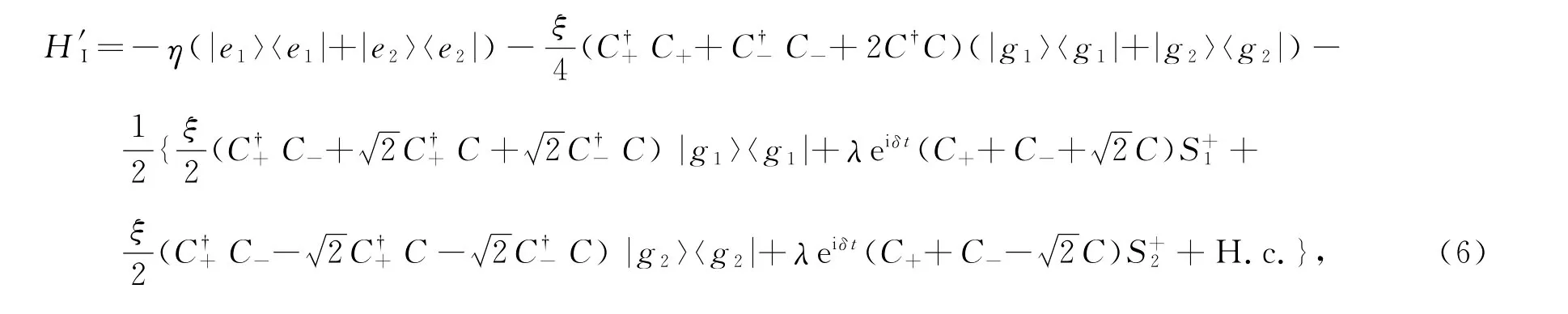
和




且基于薛定谔方程(ħ=1)

2个原子1,2的不同初始态分别演化为:

2 原子——经典微波场的相互作用
原子与经典微波场的相互作用使得原子产生下面的幺正旋转变换[1,10]:

上式为1个单比特量子门,且有φ=Ωt/2.将沿着x,y和z轴旋转的基本旋转门定义为[11]:
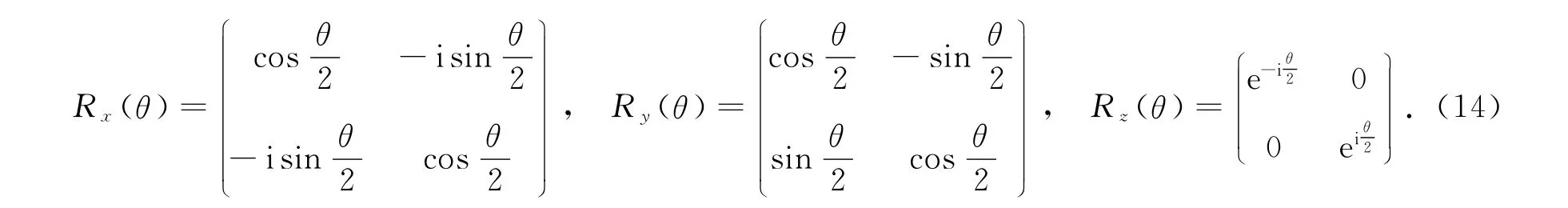
因此Rα(θ)(α=x,y,z)门可由经典微波脉冲实现:

相似地,相位门S和哈德马门H 可由经典微波脉冲实现:

3 执行两比特离散量子傅立叶变换
假设2个原子初始时处于量子态:a0|gg〉12+a1|ge〉12+a2|eg〉12+a3|ee〉12,且2个腔模和光纤模初始时处于真空态.执行两比特离散量子傅立叶变换的详细过程如下:
步骤1 让原子1经过一系列经典场使得原子1能经历旋转操作H 和Rz(π/4),这一过程可由原子 -微波共振相互作用实现.
步骤2 让原子1经过2次经典场分别实现跃迁|g〉→|e〉和|e〉→|r〉.适当选择经典场的振幅和相位使原子1经历下面的跃迁过程:

步骤3 让原子1和2分别进入2个由光纤连接的腔,且使2个腔分别处于拉比频率为Ω的经典场的驱动.经过相互作用时间χt=π后,原子1和2离开腔,因此有
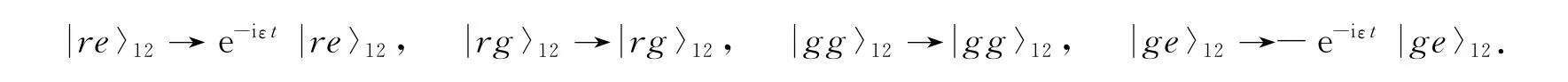
步骤5 利用经典微波脉冲驱动原子1和2使得原子1分别经历变换Rz(-π/4),H和Rz(-π/2),原子2经历变换Rz(-π/4).
步骤6 让原子1和2分别进入2个由光纤连接的腔,且使2个腔分别处于拉比频率为Ω的经典场的驱动.经过相互作用时间χt=π/2后,原子1和2离开腔,有

步骤7 让原子1和2经过一系列经典场以使原子1和2分别经历变换S和H.经过这一过程后,1个两比特离散量子傅立叶变换得以实现.
4 结论
本文提出了利用光纤连接处于经典场驱动下的2个腔系统执行两比特离散量子傅立叶变换的方案,该方案的实现需满足条件.在此条件下,原子的自发辐射和腔衰减的影响可忽略不计,而且该两比特方案可推广至N 比特离散量子傅立叶变换.
[1] Scully M O,Zubairy M S.Cavity QED implementation of the discrete quantum Fourier transform[J].Phys Rev A,2002,65:052324(4).
[2] Wang H F,Zhang S,Yeon K H.Implementing quantum discrete Fourier transform by using cavity quantum electrodynamics[J].J Korean Phys Soc,2008,53:1787-1790.
[3] Wang H F,Shao X Q,Zhao Y F,et al.Protocol and quantum circuit for implementing the N-bit discrete quantum Fourier transform in cavity QED[J].J Phys B:At Mol Opt Phys,2010,43:065503(7).
[4] Wang H F,Zhu A D,Zhang S,et al.Simple implementation of discrete quantum Fourier transform via cavity quantum electrodynamics[J].New J Phys,2011,13:013021(11).
[5] Weinstein Y S,Pravia M A,Fortunato E M,et al.Implementation of the quantum Fourier transform[J].Phys Rev Lett,2001,86:1889-1891.
[6] Barak R,Ben-Aryeh Y.Quantum fast Fourier transform and quantum computation by linear optics[J].J Opt Soc Am B,2007,24:231-240.
[7] Howell J C,Yeazell J A.Reducing the complexity of linear optics quantum circuits[J].Phys Rev A,2000,61:052303(5).
[8] Serafini A,Mancini S,Bose S.Distributed quantum computation via optical fibers[J].Phys Rev Lett,2006,96:010503(4).
[9] Zheng S B,Yang C P,Nori F.Arbitrary control of coherent dynamics for distant qubits in a quantum network[J].Phys Rev A,2010,82:042327(6).
[10] Imamoglu A,Awschalom D D,Burkard G,et al.Quantum information processing using quantum dot spins and cavity QED[J].Phys Rev Lett,1999,83:4204-4207.
[11] Raimond J M,Brune M,Haroche S.Manipulating quantum entanglement with atoms and photons in a cavity[J].Rev Mod Phys,2001,73:565-582.
[12] Barenco A,Bennett C H,Cleve R,et al.Elementary gates for quantum computation[J].Phys Rev A,1995,52:3457-3467.
Implementation of the two-qubit discrete quantum Fourier transform with optical-fiber-connected cavities
ZHANG Ying-qiao
(Department of Physics,College of Science,Yanbian University,Yanji 133002,China)
Scheme on implementation of the two-qubit discrete quantum Fourier transform(DQFT)is proposed based on two optical-fiber-connected cavities,which are,respectively,driven by two classical fields.The scheme is finished by sending two atoms,alternatively,through a series of classical fields and optical-fiberconnected cavities.Furthermore,the two-qubit scheme can be used to the N-qubit DQFT.
discrete quantum Fourier transform;cavity QED;optical fiber
O431
A
1004-4353(2012)03-0200-04
20120705 作者简介:张英俏(1978—),女,理学博士,讲师,研究方向为量子信息学.
国家自然科学基金科学部主任基金资助项目(11147174);延边大学科技发展计划项目(601010024)

