环境责任保险精算定价实证研究

游桂云，戴蕾奇，张 蕾

（1.中国海洋大学 经济学院，山东 青岛 266100；2.对外经济贸易大学 保险学院，北京 100029）

0 引言

环境问题已成为人类面对的共同难题和制约社会发展的重要因素。在环境污染事故高发的现实背景下，社会各界对如何采取综合手段加强污染事故防范和处理问题给予了高度关注，其中被广泛推崇的措施之一就是环境责任保险制度。环境责任保险是一种运用现代保险制度解决环境问题的经济政策。国际经验表明，实施环境责任保险是维护污染受害者合法权益、提高防范环境风险的有效手段。但由于环境问题本身的复杂性与交叉性，使得环境责任保险具有风险异质性高、承保范围限制严格、事故损失难以确定等特点，这使得环境责任保险费率的厘定与其他责任保险相比，技术更复杂、要求更高，因此对环境责任保险定价理论的研究具有重大意义。目前，环境责任保险在我国还是新生事物，并且我国金融市场的发展并不完善。与国外发达国家的保险市场相比，我国保险产品相对单一，投资渠道也非常有限，精算定价理论一直在我国保险实务中居于主导地位。

因此在充分考虑环境责任保险定价难点和我国保险市场发展现状后，本文针对环境责任保险定价的难点，对环境责任保险费率精算厘定技术进行理论探索，并以化学原料与化学制品行业为例进行实证研究。

1 环境责任保险精算定价过程

环境责任保险在公众责任险的基础上发展而来，本文借鉴公众责任险定价中广泛应用的精算定价理论，确定环境责任保险精算定价过程。其定价过程主要包括纯费率的测算和附加费用的测算。

1.1 纯费率的测算

在纯费率的测算中，损失数据分布的拟合是最为基础和核心的工作，包括损失次数和损失金额的拟合。常见的损失次数模型有泊松分布、二项分布和负二项分布等；损失金额模型有指数分布、对数正态分布、伽玛分布、帕累托分布与威尔分布等[1]。在环境责任保险的损失拟合中，具体选择哪种分布，需根据损失数据的特征进行选择。损失次数与损失金额的拟合过程可分为如下几步：

1.1.1 模型选择

对损失数据进行整理，计算数据的样本均值、方差、分位点等，根据这些样本数据选择一种概率分布作为损失的分布类型。例如，拟合损失次数时，根据计算出的样本均值与样本方差的大小关系初步判断样本数据服从哪种分布，当样本均值大于方差时可选择二项分布，等于方差时则可用泊松分布。

在环境责任保险中，由于环境污染本身的复杂性，企业因污染环境而承担的损害赔偿数额有时会很大，这使得在损失数据拟合时经常会遇到一些损失数额巨大的观测值。对于这种情况一般有两种方法解决：一是对损失数据进行分割，找到一个适当的门限值，然后分别对两部分数据进行拟合[2]。二是直接对全部损失数据进行拟合，得到一个能精确拟合损失数据中心部分的分布模型，再综合考虑损失数据和索赔数据的关系，进行调整。具体选用哪种方法可以根据数据拟合的结果进行选择。

1.1.2 参数估计

初步选择了损失模型后，需要对模型的参数进行估计，常用的估计方法有矩估计法和最大似然估计法。矩估计法是用样本矩来作为总体矩的估计，令μi=Ai,i=1,2,...,k，k为未知数的个数，通过解方程组得到参数的估计量。而最大似然估计法是通过构造似然函数L(θ1,θ2,...,θk)=L(x1,x2,...,xn;θ1,θ2,...,θk)，求似然函数达到最大值时的参数值，以此作为模型参数的估计量。

1.1.3 拟合检验

拟合检验的基本原理是设立检验统计量，以对模型的分布函数和经验分布函数之间的接近程度进行度量，通过检验统计量与临界值的比较，判断分布的拟合是否合理。常用的方法有χ2拟合优度检验、Kolmogorov-Smirnov检验[3（]简称K-S检验）。χ2拟合优度检验的检验统计量为，其中n为样本量，=F∗(xi)-F∗(xi-1)为观测值落在 xi-1到 xi区间的概率，pni=Fn(xi)-Fn(xi-1)为经验分布的概率。该检验的临界值由相应的卡方分布决定，其自由度为k-j-1（j为参数的个数）。通过检验统计量与临界值的比较检验损失分布的可行性。

1.1.4 纯费率的确定

通过对损失次数和损失金额的拟合得出保险合同在保险期限内保险事故发生的频率P和损失金额E(X)，在计算损失金额E(X)时，充分考虑环境责任保险的赔付限额和免赔额对E(X)的影响。然后确定纯费率为：

其中A为保险金额,E(S)为保险期限内每份保单的预期索赔额：

1.2 附加费用的测算

1.2.1 风险附加

如果按照纯保费收取保费，即使不考虑费用附加，保险公司也会有50%的可能性亏损，甚至破产。为了避免这种情况的出现，需要在纯保费基础上附加一定的费用，减小保险公司破产概率，这就是风险附加。风险附加又称第一附加保险费，它是为防止各年度实际保险金额损失率偏离保险金额损失率期望值，在纯费率基础上附加的费率。它的目的是使纯费率与保险人的实际保险金额损失率更为接近，以应付异常的损失赔付，保证保险企业的财务稳定性。风险附加是以纯保费为基础计算的，用以保障保险公司不会亏损破产。设保险公司共有n个保单，Si为第i个保单损失的随机变量，预期损失为E(S)，则风险附加保费为F=k×E(S)，此时保险公司保持不亏损的概率为

当保险公司的保单数量达到一定数量时，可以应用大数定律，计算在不同的保障程度α下所需要的风险附加。

环境责任保险的风险异质性突出，风险附加的设置就更加必要。环境责任保险的风险可测性较差，且常常与巨灾密切联系，因此应取较高的风险附加，即取较大的α值，以防止保险公司承担的风险过大，导致保险公司破产。

1.2.2 费用附加

费用附加是保险公司为使各项业务正常运行而收取的费用，主要包括营业费用、手续费、佣金、预期承保利润等。费用附加中有的部分与保费收入有关，如手续费、佣金和部分营业费用，称为可变费用；有些费用则不随保费的变化而变动，或者变动不大，如营业费用中办公室的租金、管理费用等，又称为固定费用。在实际定价中，由于费用附加的数据可得性差，或者得到数据的成本太大，常以风险保费的一定比例进行计算。虽然费用附加的变化并非与风险保费的变化保持一致，按照风险保费一定比例确定费用附加不尽合理，但考虑到同类险种在一段时间内，风险保费和费用附加都不会有大的变化，二者之间存在一定的比例关系，利用风险保费确定费用附加具有一定的合理性，在没有其他操作性更好的方法时，用这种方法确定附加费用是适合和有效的。

环境责任保险的正外部性很强，具有一定的社会公益性，是准公共产品。环境责任保险在避免企业承担环境责任风险的同时，更加保护了一般社会公众的环境利益。因此环境责任保险并非是纯商业性质，具有一定的政策性。政府应该在税收、费用等方面给予一定的优惠，从而环境责任保险的费用附加可以确定在一个较低水平上。

1.3 总费率的确定

通过对纯费率和附加费用的测算，确定总费率，其公式为：

2 实证研究

由环境责任保险风险异质性突出的特点可知，不同行业的环境责任风险迥异，环境责任保险费率水平必然不同。但以行业为标准进行分类，各行业的环境责任保险费率厘定思路却是一致的。本文选择某一行业进行实证研究，在测算该行业环境责任保险费率水平的同时，也展示了一般行业环境责任保险费率精算厘定的思路和过程。

2.1 数据来源与数据处理

2.1.1 行业的选择

环境责任保险正外部性的特征要求强制模式支持，同时，环境责任保险在我国还是新生事物，有一个循序渐进的推广过程。综合考虑两方面的因素，作者认为应该在污染严重、污染风险大的行业采用全行业的法定强制保险，而在一般行业采用自愿模式。根据国家环境统计年报的统计，化学原料与化学制品行业的环境污染事故远远高于其它行业，属于高污染的行业。因此本文选取化学原料与化学制品行业为研究对象进行实证研究。

2.1.2 参保企业范围的确定

在假设化学原料与化学制品行业实施强制环境责任保险的条件下，可以认为该行业的企业全部参加环境责任保险；根据分类定价的思想，作者将经营规模相当的行业进行统一风险分级，将统计对象确定在化学原料与化学制品行业中国有企业及规模以上非国有企业。因此，本文以2010年《中国统计年鉴》中化学原料与化学制品行业的国有企业及规模以上非国有企业的数量为研究样本，最终企业的数量确定为22981家。

2.1.3 损失数据的获得

由于我国环境污染事故数据积累较少，这对损失数据的获得造成了极大的障碍，对于这一难点，作者进行了如下考虑：

（1）考虑官方公布的权威数据。可得的官方数据包括：国家统计年鉴、国家环境统计年报等，但查阅官方公布数据后，发现官方数据缺少行业的环境污染损失事件次数和损失金额统计，即从目前官方发布的数据不能获得所需数据。因此只能将数据采集转向其它途径，包括学者研究。

（2）考虑从环境责任保险实践中获得数据。我国的环境责任保险只在少数几个城市有试点，试点期间环境责任保险业务量少，投保企业数量太少。从环境责任保险的实践历程来看，真正来自于保险行业的数据基本不可得，研究受阻，从保险部门采集数据的思路也不可行。

（3）尝试从地方环保部门查找数据，效果也不理想。因此，将研究思路转向学者研究。通过查阅相关文献发现，从2000年开始，王亚军等定期在《安全与环境学报》上发布了国内环境事件统计，对报导的环境污染事件进行汇总。目前，他们已统计了从2000～2010年8月份的国内环境污染事件。其中，2000～2003年的国内环境事件是以3个月或4个月甚至1年的事件为一个统计区间；从2004年开始，王亚军等以两个月为一个区间，对国内的环境事件进行了较详细统计。目前，该统计由于连贯性、系统性，已成为环境科学研究者的重要参考资料，在一定程度上填补了国家官方统计的空白。作者深知该统计有明显的局限性，但在目前无官方数据提供的限制下，该文献的确不可替代。需要强调的是，在此替代下，本文将环境污染事件限定在突发性、破坏性的环境事件，不包括渐续性事件，也不包括长尾事件。

在上述资料基础之上，对收集的数据做如下选择和处理：

（1）关于统计的时间区间选择

2000～2003年的国内环境事件是以3个月或4个月甚至1年的事件为一个统计区间，反映了这一段时间内的统计数据不够全面。从2004年开始，王亚军等以两个月为一个区间，对国内的环境事件进行了较详细统计。因此选取2004年1月至2010年8月的污染事件统计，以每两个月为一个样本空间，共得到40个样本。

（2）关于事件损失计算

在环境事件统计文献中，只是根据事件顺序对报道的环境污染事件进行了梳理，并没有对每次事故造成的损失进行统计，将事件统计转换为损失统计是工作的难点。为此，根据王亚军等的统计资料查找到每起事故最原始的报导和相对充分的信息，再根据国家有关标准，对于每次事故的损失金额进行计算汇总（见表1）。

2.2 纯费率的确定

2.2.1 免赔额和赔付限额的确定

根据化学原料与化学制品行业的企业规模以及环境污染事故的损失统计，本文选取200万元作为赔付限额，可以对近86%的保险事故进行完全补偿，其余事故起到一定的补偿作用。同时，由于每个投保人在保险期间内往往至多发生一次环境责任事故，可以认为保险金额就等于赔付限额，因此，将保险金额也设为200万元。免赔额方面，共统计了129起化学原料与化学制品行业环境污染事故，115起属于损失在5万元以上的事故，约占总事故的90%，因此选取5万元作为绝对免赔额。

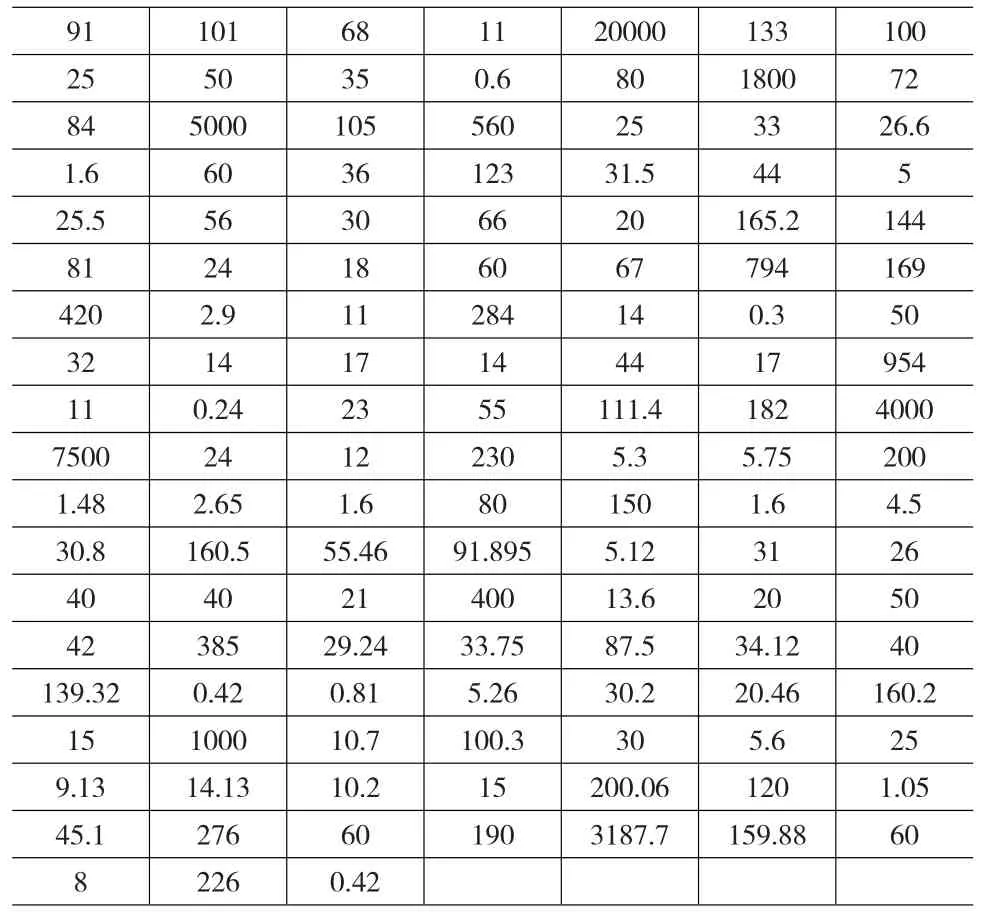
表1 2004～2010年8月化学原料与化学制品行业环境污染事故损失金额（万元）

2.2.2 索赔次数的拟合及预测

发生损失并不一定发生索赔，当损失额小于免赔额时，并不会发生索赔，因此，本文对化学原料与化工制品行业的损失事故次数进行了处理：以2004年1月到2010年8月的环境污染事故数为基础，剔除损失额在五万元以下的事故，以两个月为一个样本空间，将数据整理如表2所示。

表2 2004～2010年8月各样本空间事故数

根据表2数据计算得，样本的均值为2.875，方差为2.709，方差小于均值，本文选择二项分布对索赔次数进行拟合。由于企业之间发生环境污染事故的相关性很小甚至完全不相关，因此假定每家企业事故的发生是相互独立的，且都服从（0，1）分布，即

在第一个样本空间，即2004年01～02月份中，用极大似然估计法求取参数p1，极大似然函数为：

同理可求得在第i(1≤i≤40)个样本空间的参数pi(1≤i≤40)，取各样本空间所得参数的平均值得，每个样本空间发生的次数值 c=22981=2.875 。

对该分布进行拟合优度检验：

所以该分布能显著代表事故发生的概率，即该行业环境污染事故发生的次数符合=1.251×10-4的（0，1）分布。由于选取的样本空间为2个月，且王亚军，李生才等在《安全与环境学报》上统计的2004～2010年化学原料与化学制品行业的污染事故数偏少，每年统计的事故数相当于同《中国环境统计公报》统计数据的1/4。因此，本文综合考虑信息不对称、统计标准不一致等因素，将发生事故数调至2004～2010年的《国内环境事件》统计次数的4倍，即以《中国环境统计公报》统计数量为准。综上对事故概率进行修正后的数值应为：

2.2.3 损失金额的拟合及预测

化学原料与化学制品行业每次发生事故的损失金额为Xi(1≤i≤129)，对损失数据取对数得Yi=ln Xi,1≤i≤129，假设变量Y 服从正态分布，即Y～N(μ,σ2)。利用K-S对其进行检验（检验结果如表3所示）。

表3 Kolmogorov-Smirnov检验

由K-S检验结果得出Sig=0.4＞0.05，证明可以接受变量Y服从正态分布的假设。对数据Y，以1为组距进行分组，得表4。

对表4中的最后一列加总求和即为拟合优度检验的χ2值，显著性检验 χ2=8.65＜χ0.052(8-2-1)=11.07，由此可得损失金额显著服从μ=3.6722，σ=1.97988的对数正态分布，即

考虑5万元免赔额和200万元赔付限额的影响，每份保单的预期损失金额为：

2.2.4 纯费率的确定通过对损失次数和损失金额的拟合测算得出，保险合同在保险期限内的事故发生的频率P和损失金额为E(X)，将P和E(X)代入公式（2）得，每份保单的预期赔付额为：

表4 参数检验及损失金额预测

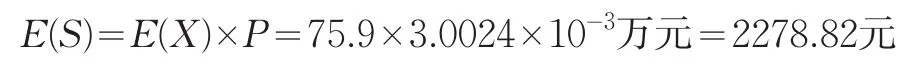
代入公式（1）得出环境责任保险的纯费率：

2.3 附加费用的确定

2.3.1 风险附加费用

由公式（2）和（3）变形可得，保险公司不发生亏损的概率为P[Xi＜(1+k)E(Xi)]=α。已知化学原料与化学制品行业每家企业的损失额服从对数正态分布，即Xi～LN(μ,σ2)，其中 μ=3.6722，σ=1.97988。取不同的 α 水平，计算风险附加的系数k得表5。

表5 风险附加系数表

由于环境责任保险的风险异质性突出，且化学原料与化学制品行业属于高污染行业，保险公司承担的风险较大，综合考虑科学性与可行性等多种因素，取α=97%，则风险附加系数k=21.1316。

2.3.2 费用附加的测算

费用附加应以营业费用、手续费、佣金等费用的总额加以确定，但由于数据的可得性差，或者得到数据的成本太大，在此取中国保险业市场财险业务2004～2010年的费用支出与赔付支出比值（见表6）的平均值作为环境责任保险定价中的费用附加率β。

表6 2004～2010年我国财险业务的费用支出与赔付支出表

取表6最后一列的平均值得到环境责任保险的费用附加率为β=0.3745。

2.4 总费率的确定

代入公式(4)得，化学原料与化学制品行业的环境责任保险总费率为：

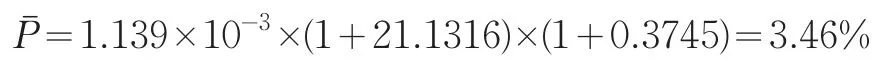
3 研究结论

运用精算方法得到化学原料与化学制品行业环境责任保险的费率为3.46%，与其他责任保险的费率相比较，属于合理范围。实证研究表明，精算定价为环境责任保险费率厘定提供了理论思路。

本文的主要贡献不仅在于厘定了化学原料与化学制品行业环境责任保险的费率，对该行业环境责任保险费率水平的设定具有借鉴意义；更在于正面回答了如何解决环境责任保险定价难的问题。针对环境责任保险定价过程中各个环节所面临的困难，本文提供了解决思路，如针对环境责任保险风险异质性突出的特点，运用分类法将企业进行风险等级的划分，并在纯费率的基础上设置一个较高的风险附加系数；针对事故数据积累过少的难点，根据国家相关标准对王亚军等统计的环境污染事故进行损失计算，并根据《中国环境统计公报》的相关数据进行调整等。未来，要提高结论在经营层面的可信性，可从两个角度补充工作：第一，注重数据的采集和积累，增加样本数量；第二，将模型所考虑的因素加以补充，使其与实际更加吻合。作者认为，与具体的定价结果相比较，定价思路的摸索与探讨具有同样的学术价值。

[1]孙佳美.非寿险精算理论与实验[M].北京：中国财政经济出版社,2008.

[2]刘曼莉，李兴绪.非寿险精算中的数据尾部拟合与保费厘定[J].统计与决策,2011,(4).

[3]Stuart A.Klugman，Harry H.Panjer，Gordon E.Willmot.损失模型从数据到决策[M].吴岚译.北京：人民邮电出版社,2009.

[4]Krzysztof Burnecki，Grzegorz Kukla，Rafa Weron.Property Insurance Loss Distributions[J].Statistical Mechanics and Its Applications,2000,(287).

[5]Gómez-DénizJosé María Sarabia，Enrique Calderín-Ojeda.A New Discrete Distribution with Actuarial Applications[J].Mathematics and Economics,2011,(3).

[6]安莹,李生才.2010年7-8月国内环境事件[J].安全与环境学报,2010,(50).

[7]钟桢，孟生旺.基于伽玛与对数正态分布假设下的广义线性模型的比较和应用[J].数理统计与管理,2010,29(3).

[8]张鸿雁,邓华.二项分布模型系数的确定[J].经济数学,2006,23(1).