投资组合模型的动态规划解法
陈国华,廖小莲,吴 娜
(湖南人文科技学院 数学系,湖南 娄底 417000)
0 引言
投资组合选择在企业经济活动中有着重要的指导作用。Markowitz[1]的均值方差理论为近代证券投资组合理论奠定了基础。而均值方差模型的实质上是一个以二次规划优化模型。为了减少参数、简化计算,不少文献[2,3]提出了线性化投资组合模型,但是,将一定数量的资金有选择地投入多种产业,可以作为一个多阶段决策过程,即动态规划模型。利用动态规划研究投资组合问题的方法已有一些研究[5,6,7]。在文[5]中,作者对均值-方差模型建立一种动态规划模型和递推算法。文[6]对多阶段资产投资问题,给出了在满足一定的风险承受能力情况下的、以总收益尽可能大为决策目标的资产投资组合模型,利用动态规划方法求得多阶段投资的最优投资组合,文[7]引导投资者选择最佳投资策略,将动态规划模型应用于组合投资理论,文[8]在允许卖空的情况下,以终端财富最大化为目标,通过建立辅助问题,利用逆序动态规划的求解方法,文[9]利用动态规划方法解决带交易费用的均差模型,给出了有交易费用均差模型的解析解。
1 投资组合模型模型的建立
设有资金M,可在一个时期内投资于市场上的n种资产A1,A2,…,An或存款银行A0,用指标净收益尽可能大与总风险尽可能小来衡量投资方案的优劣,假定通过统计分析,得到各资产Ai的平均收益率为ri,与风险损失qi。银行存款A0的利率为r0且无风险(q0=0)。购买资产Ai的交易费是分段函数:收费率为 pi,但当购买量不足ui时,交易费按购买ui计算。因此,购买Ai的收益须减去交易费之后得到净收益。在本文中,我们以投资各个Ai的风险损失和来度量总体风险。设xi表示购买资产Ai的资金(1 ≤i≤n),x0为银行存款。则交易费可表为:

在本文中我们利用线性加权法把双目标规划问题转化为单目标规划问题。考虑到风险的特殊性,我们附加一个约束从而得到如下的投资组合模型:
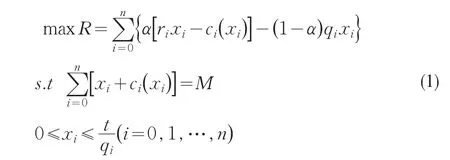
其中t为参变量。由于ci(xi)是分段线性函数(在xi=0处不连续),模型为非线性规划问题,下面我们利用动态规划来求解。
2 模型的动态规划解法
在模型(1)中,对n+1种资产的资金分配看成n+1阶段决策过程,其中xi作为第i阶段的决策变量,从第0阶段到第i阶段所分配的资金,记为si,作为第i阶段的状态变量。那么,n+1阶段所分配的总资金为si=M,且状态转移规则为:

当状态变量si给定时,决策变量xi的取值范围称为第i阶段的决策集,记为Di()Si。根据上面的模型,我们有:

在每一阶段决策时都要求xi∈Di(si)。这样一来,静态模型(1)就转化为一个动态决策过程。
2.1 动态规划算法
根据前面的分析,总资金M作为第n+1阶段的终止状态,我们利用动态规划的顺推算法来求解。设最优值函数fk(s)=直到第k阶段投资金额不超过s的最大收益,得到:

根据动态规划的最优化原理,得到最优值函数序列满足的递推方程如下:
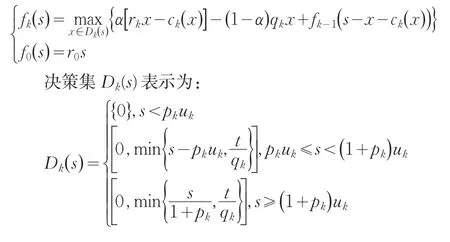
3 数值算例
假使经过统计分析,决策者已获得了如下的数据(见表1)。

表1
i可以不考虑起点金融ui,那么它就可以用线性函数pix 来代替。)
首先将M离散化,插入分点0,0.5,1,1.5,2=M
进行回代,得出最优解:
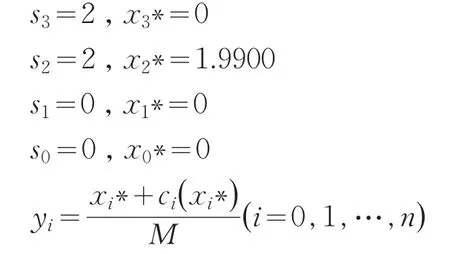
得到最优投资组合(y0,y1,y2,y3)=(0 ,0,1,0 ),即:向A2投资200万元。
4 结束语
投资组合是现实社会的一个广泛而重要的课题,本文主要探讨了将动态规划最优性原理应用于投资组合的研究,针对资金分配、资产投资及多目标资产投资建立了数学规划模型,利用动态规划对问题进行了求解,数值算例说明了模型的可行性,对指导投资决策具有一定的知道意义。
[1]Markowitz.H.M.Portfolio[J].Journal of Finance,1952,(7).
[2]陈炜,杨玲.具有交易费用的均值一极大极小半绝对偏差投资组合模型[J].首都经济贸易大学学报,2009,(6).
[3]陈国华,廖小莲.基于区间规划的投资组合模型[J].辽宁工程技术大学学报(自然科学版),2010,29(5).
[4]丁元耀,贾让成.一种证券组合的投资选择建模[J].运筹与管理,1999,8(2).
[5]林浩,投资组合问题的动态规划方法[J].运筹与管理,2000,9(3).
[6]宿洁,刘家壮.多阶段资产投资的动态规划决策模型[J].中国管理科学,2001,9(3).
[7]伍勇,刘春.动态规划模型在“组合投资”理论中的应用[J].北京机械工业学院学报,2008,23(2).
[8]孙世杰,高岩.摩擦市场下多阶段投资组合的均值方差模型[J].上海理工大学学报,2008,30(4).
[9]花秋玲,苏孟龙,吕显瑞,王锐.带交易费用投资组合问题的动态规划方法[J].吉林大学学报(理学版),2009,47(5).

