基于复杂网络的高速公路运营效率评价＊

韩建飞，宗 刚

（北京工业大学 经济与管理学院，北京 100124）

高速公路建设一直是国家和地方基础设施建设的重要方面，它可以从多个方面带动经济的增长。近10年来，我国高速公路快速发展，全国和各省（市、区）高速公路网正逐步形成。随着我国经济的快速发展，2000年以后高速公路通车里程也呈现出快速增长的趋势，截止到2010年底，我国高速公路通车总里程达74 000公里，居世界第二位。高速公路的建设与运营对区域经济产生了积极的作用，然而与此同时，其自身的运营效率成为制约其发展的重要问题。虽然高速公路一直被称为“暴力”行业，但在建设时期缺少资本金的情况下，大部分高速公路的建设出现了资产负债率高的现象。截至2011年第一季度，我国19家上市路桥公司总资产负债额高达1 000亿元，其中资产负债率超过50%的有5家。如果高速公路建成之后而没有足够的车流量保证通行费的收入，那么由于资产负债率高以及部分路段利用效率低等引起的问题将是十分危险的。因此，高速公路目前正处于运营发展的重要转折期，“十二五”期间我国高速公路总里程将达10.8万公里，在此期间，如何合理规划、建设和运营，在长时间内都将会是有关高速公路健康发展的重要议题。

目前，对高速公路网的研究大多基于图论及分形理论，将公路网抽象地描述为广义拓扑图，并用相关的度量指标进行描述。这些指标对于定量研究交通网络的结构特征具有一定的积极作用，但在描述公路网结构的整体形态及复杂性，尤其是在大型交通网络中线路的联接性和关联性识别方面尚存在不足［1］。结构特性是复杂道路交通网络研究的一项重要内容。不少学者对此进行了研究。如Csanyi和Szndroi认为公路网是一个按幂律增长的分型网络［2］；Jiang和Claramunt采用连通性、平均路径长度和聚类系数等指标刻画复杂交通网络的特征［3］；邓亚娟、杨云峰采用对偶拓扑方法，将公路路段按照路名抽象为节点，将交叉口抽象为网络边，对实际公路公路网进行了拓扑结构转换［4］。

对高速公路评价方面的现有研究主要集中于以下几个方面：一是高速公路对区域经济、社会以及环境的影响等方面的评价；二是高速公路的安全性评价，包括通行能力评价，交通安全评价，路段安全评价，特殊区域的安全性评价等方面；三是高速公路建设项目的评价，主要是指建设项目管理、绩效评价等；四是高速公路运营效率、服务质量等方面的评价。评价高速公路自身运营效率的相关研究也因运用方法的不同而各异，杨明等为解决模糊综合评价在运营效益评价过程中存在的很难克服指标权重设置中的主观性问题，其引进了统计学理论中的支持向量机，建立了高速公路企业的运营效益评价的支持向量机评价模型［5］。谢洪新等应用多层次分析法和神经网络模型，对高速公路网评价指标及综合评价方法进行了研究［6］。刘伟铭、付凌峰研究了高速公路最佳运营区域划分的量化分析方法，通过层次聚类分析，获得分区备选方案，最后通过建立方案的评价指标体系以及方案选择的多目标决策模型，获得最佳运营区域划分方案［7］。

文献回顾表明，现有高速公路运营评价的研究主要集中在高速公路对社会、经济以及环境的影响和涉及道路安全方面的工程性问题方面，对高速公路自身运营效率研究较少，已有研究也主要集中于对高速公路投资回收以及运营效益等进行评价，鲜有对不同属性路段运营效率的研究。此外，高速公路网方面的研究也主要集中在网络无标度结构特性的考察，对网络特征节点实际意义进行研究的较少。山西省高速公路的发展起步较早，高速公路建设对区域经济发展的促进作用明显，网络结构初具规模。因此，本文在总结前人研究成果的基础上，结合复杂网络理论与灰色系统理论，对山西高速公路的运营效率进行系统的评价分析，从中发现高速公路运营过程中的问题，验证高速公路网中不同属性节点的实际特征，并进一步验证无标度网络理论中统计参量与实际参量之间的关系，对高速公路的建设和运营管理具有一定的指导意义。

一、模型概述

（一）复杂网络

复杂网络理论研究始于20世纪60年代由著名数学家Erdos和Renyi提出的ER随机图模型。复杂网络不是由节点及其关系组成的图，而是关于图的集合，或关于图的随机过程。从这个角度上讲，复杂网络是图的延伸。复杂网络模型主要包括小世界模型和无标度网络。

Barabási和 Albert［8］建立的BA 复杂网络模型是分析无标度网络最常用的一种复杂网络动力学模型。其构造的算法包括：增长，从一个具有m0个节点的网络开始，每次引入一个新的节点，并且连到m个已存在的节点上，这里m≤m0；优先联接，一个新节点与一个已存在的节点i相联接的概率∏i与节点i的度ki、节点j的度kj之间满足如下关系，即

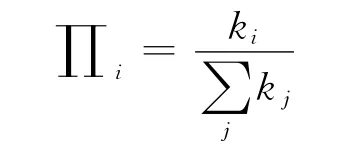
在经过t步之后，这种算法产生一个N＝t＋m0个节点、mt条边的网络。

度是单独节点的属性中最简单而又最重要的概念。一个节点所拥有的度是该节点与其他节点相关联的边数，度是描述网络局部特征性的基本参数。网络中并不是所有节点都具有相同的度，网络系统各节点度可以用一个分布函数p（k）（度分布函数）描述，节点的度分布是指网络度为k的节点的概率p（k）随节点度k的变化规律。无标度网络的度分布遵循幂律分布，即任何节点与其他k个节点相连结的概率正比于k－λ。度分布函数反映了网络系统的宏观统计特性。在系统不断演化时，分析节点之间的度分布，可以把握系统内部各个元素之间关系的变化程度，也可以根据这一变化来预测未来系统的拓扑结构。

（二）灰色综合评价

信息不完全确知的系统称为灰色系统。控制论中，信息充足、确定的为白色，信息缺乏、不确定的为黑色，灰色系统是介于两者之间的中间系统。灰色理论应用最广泛的是关联度分析方法［9］。关联度分析是对分析系统中各元素之间关联程度或相似程度进行分析的一种方法。灰色关联度方法分析的具体步骤如下：第一，确定比较数列和参考数列；第二，确定各指标值对应的权重；第三，指标值的规范化处理；第四，计算灰色加权关联度；第五，计算综合评价结果，进行评价分析。根据综合评价结果，对各评价对象进行排序，关联度越大其评价结果越好［10］。

二、实证分析

（一）高速公路网络构建

高速公路网络除具有绝大多数复杂网络的特征外，作为空间网络还具有不同于抽象网络的特性，这些特性决定了高速公路网络的拓扑性质。具体可以归纳为：高速公路交通网络的节点存在于二维地理空间，且有明确的位置；高速公路网络中的边是一种实体联接，具有明确意义，并不是抽象空间中所定义的关系，能够明确表示线路之间的相互关系，线路在整个网络中的重要程度以及网络的局部和全局效率；高速公路交通网络中节点的长程联接需要一定成本，这一特性直接影响着高速公路网络出现小世界行为的可能性；高速公路交通网络中单一节点所能联接的边的数目受到物理空间的限制，这种限制会影响到网络的度分布。

关于模型假设数据来源，本文研究的数据由山西省高速公路网2007年以后通车的27条（包括21条政府经营性高速公路，其中一条2008年底通车；6BOT模式经营性公路）高速公路组成，并将高速公路网络视为无向网络，即如果从A高速路可以到达B高速路，相应地从B高速路也可以到达A高速路。具体情况如下：第一，采用的数据包括政府经营和非政府经营的所有高速公路；第二，以已投入运营的每条高速公路作为节点，即27条高速公路处理为27个节点。

关于模型假设，高速公路规划、建设和运营是一个复杂的系统工程，涉及的因素复杂多样，本文主要考察高速公路网络的生长情况以及网路中节点数增加，平均度数增长，集聚系数的提高与高速公路车辆通行量以及经济增长之间的相关性。本文对高速网络模型作出如下假设，假设1：每条高速公路作用都是相等的，节点没有大小，不考虑每条高速公路的通车里程；假设2：高速公路之间有直接联接的则定义它们之间有联接，在其邻接矩阵里面关系定义为1，反之则为0；假设3：本模型以整个高速公路网络为研究对象，以整个网络的最优化为目的。

（二）高速公路网及分析

根据中国高速公路网相关数据整理获得山西省高速公路不同路段之间的关系矩阵，利用ucinet软件对山西省2008年已经通车的的路段节点及其联接情况分析发现，山西高速公路网节点的增长与联接具有无标度网络节点生长的特征。见图1、图2。

图1 山西省高速公路网络图

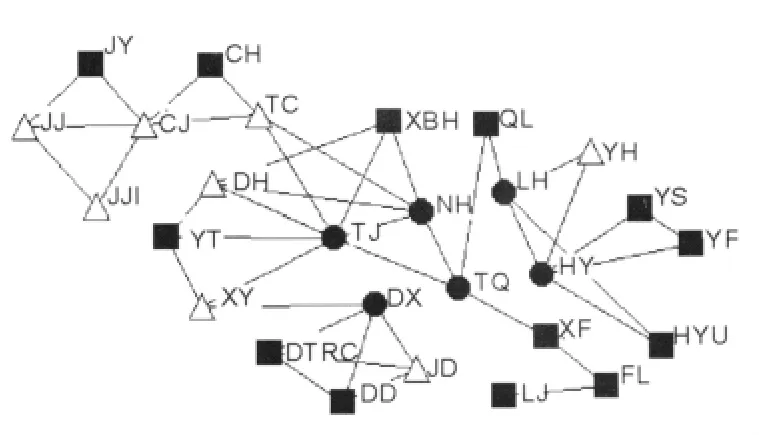
图2 山西高速公路网聚类分布图

对山西省高速公路网络的度数参量进行统计分析得出网络的平均度数为3.11，各节点的度数分布情况，见表1。

表1 高速公路网节点度数分布图

由表1可见，TJ等9个节点的度数大于网络平均度数，其余大部分节点度数均小于平均数。为减少社会投资经营的6条公路对于评价结果的干扰，本文只对政府经营的高速公路进行分析评价，与此同时，JJ路段由于2008年底通车，数据不完整，故只考虑政府经营的其他20条路段。根据度数是否大于平均度数对上述20各节点进行分类，结果见表2。

表2 高速公路节点聚类分布表

（三）高速公路灰色综合评价

1.指标体系的构建。依据系统性性、科学性以及横向可比性原则，指标体系的构建从收入、支出、资产三个方面入手。具体分为目标层（A）、中间层（B）和指标层（C），见图3。

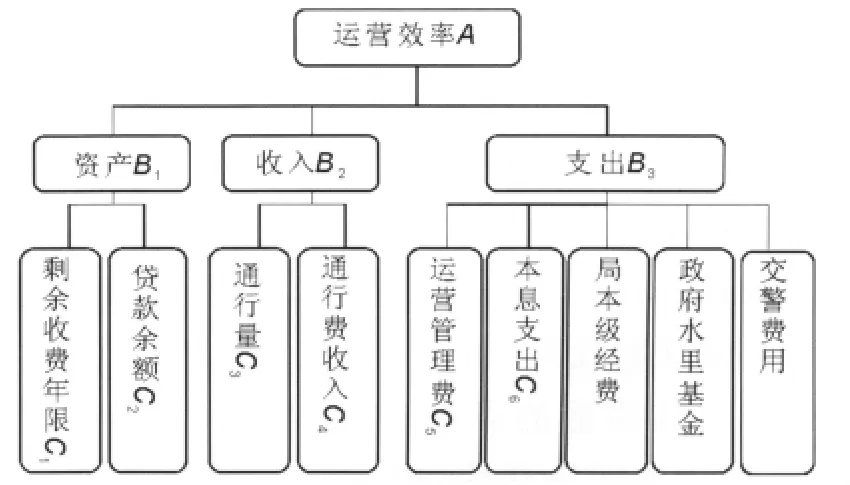
图3 高速公路运营效率评价指标体系图

由于局本级经费、政府水利基金以及交警经费的数据存在可获得性以及时间上的连续性等问题，因此在多层分析结构模型以及下面的计算过程中这些指标不在考虑之内。

2.判断矩阵构建与权重确定。建立层分析结构模型后，在各层元素中进行两两比较，构造出比较判断矩阵。判断矩阵表示针对上一层次因素，本层次与之有关因素之间相对重要性的比较［11］。然后，通过求解判断矩阵的最大特征值及其特征向量，计算得出这一组指标值的相对权重。这也证明了层次分析法的基本原理：在复杂系统研究中，构建一个层次结构模型，然后利用较少的定量信息，把决策的思维过程数学化，从而求解多目标、多准则或无结构特性的复杂决策问题。具体做法是根据判断矩阵的赋值方法，利用1～9标度方法对同一层次的指标项逐一进行考察赋值。见表3，表4。

表3 判断矩阵的赋值方法［5］

表4 判断矩阵

3.判断矩阵的一致性检验。应用层次分析法，保持判断思维的一致性是非常重要的。判断思维的一致性是专家在判断各项指标的重要性时，要求各判断矩阵之间协调一致，避免相互矛盾结果的出现。衡量不同阶判断矩阵是否具有满意的一致性，还需引入判断矩阵的平均随即一致性指标RI值。由于1，2阶判断矩阵总是具有完全一致性，所以RI只是形式上的。在多阶判断的条件下极容易出现不一致，只是不同条件下的不一致程度有所差别［12］。

引入判断矩阵最大特征根以外的其余特征根的负平均值CI，作为度量判断矩阵偏离一致性的指标。检查决策判断思维的一致性。

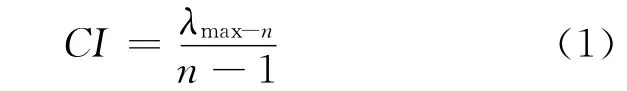
显然，当判断矩阵具有完全一致性时，CI＝0，反之亦然。当阶数＞2时，判断矩阵的一致性指标CI与同阶平均随机一致性指标RI之比即随机一致性比率CR。当

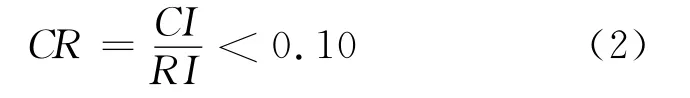
时，即判断矩阵具有满意的一致性，否则调整判断矩阵并最终使之具有一致性。本文中间层的阶数为3，所有指标层的阶数都为2。阶数n＝3时所对应的值为0.58。

通过计算，中间层A－B的一致性检验如下：

在一致性检验的基础上，结合判断矩阵计算判断矩阵的综合权重值，见表5。

表5 综合权重值

4.综合评价分析。本文采用灰色综合评价法来分析山西省高速公路运营效率水平。针对已建立的指标体系，查阅山西省高速公路分析报告，整理获得2008－2010年相关数据，见表6。

按照表2的分类，3个年份的实际数据均为当年各类数值的均值，其中实际数据中通行量、通行费收入以及运营管理费数值采用每一类路段每公里的平均费用；平均剩余年限是指每类高速公路剩余的收费年限的平均值；贷款余额比例为每一类路段剩余的贷款额占高速公路建设贷款的比例的均值；本息合计／通行费，即当年每一类路段偿还银行本金以及利息额占当年通行费收入的比例的均值。

表6 各指标实际数据

由于原始数据量纲的存在，数值较高的指标和水平较低指标都会影响综合分析的结果，因此，需要对原始数据进行标准化处理［13］。通过对原始数据量纲的量标准化处理，将各评价对象中每一项指标的最佳值作为理想对象的指标值，对不同影响因素而言，有的指标以最大为好，有的指标则以最小为好。以最佳值为基础，理想指标值整合为理想指标集。作为计算关联度系数的参考数列，利用关联分析法分别求得第i个方案的第k个指标与第k个理想指标的关联系数，在公式（3）中0＜ξ＜1，本文对赋值为0.5，据此得出各类路段2008－2010年间各指标数据间关联度系数。

式中：ξ是比较数列；Xi与参考数列；X0在第k个评价指标上的相对差值。见表7。

表7 标准化指标关联度

5.评价结果。计算灰色加权关联度，并根据其大小对各评价对象进行排序，灰色加权关联度越大说明其评价结果越好。其灰色加权关联度公式为：

式（4）中：ri为第i个评价对象对理想对象的灰色加权关联度。由表5综合权重与表7标准化数据可以得出灰色加权关联度评价结果，见图4。

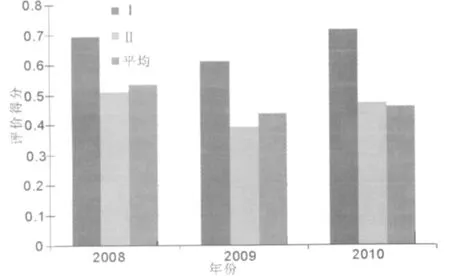
图4 评价结果对比图

从以上计算过程和结果可以看出，2008－2010年间Ⅰ类较之于Ⅱ类路段具有较好的运营效率，即高速公路网络中具有较多联接（度数大于平均度数）的少数路段的运营效率大于具有较少联接的路段（度数小于平均度数），具体排序为Ⅰ类＞平均＞Ⅱ类。此外，通过对3年评价结果的连续数据分析发现，2008年之后，Ⅰ类、Ⅱ类以及代表高速公路平均水平的高速公路的运营效率均有所下滑，但较之于2009年，2010年运营效率已有明显回升。

三、结 论

将灰色系统理论与复杂网络理论相结合并应用于高速公路网运营效率控制中是一种新的尝试。本文首先构建了山西省高速公路网络，并按照路段节点度数以及相应路段的经营性质进行聚类，在此基础上，建立了高速公路运营效率的评价指标体系，然后运用层次分析法和灰色理论相结合进行综合评价分析。评价结果表明：第一，2008－2010年3年期间山西高速公路网络中具有较多联结的节点路段评价结果明显好于联接较少的路段，即度数较大路段具有更高的运营效率。第二，联接较大的节点只是网络中较少的路段，其运营效率的好坏并不能代表全省高速公路运营效率的提高。具有较少联接的大多路段运营效率低于所有路段平均值的运营效率，这是制约高速公路运营效率进一步提高的最重要的问题之一。因此，提高区域高速公路网络的运营效率，可以进一步完善从区域高速网络结构，提高高速公路网络结构的联接较少路段的运营能力两个方面着手。

［1］杨 明，高 勇.基于支持向量机模型的高速公路运营效益评价［J］.系统工程，2009（2）：90－95.

［2］Csanyi G，Szndroi B.Fractal－small－world dichotomy in real－world network［J］.Physical Review E，2004（1）：1－5.

［3］JIANG B，CLARAMUNT C.A structural.Approach to the Model Generalisation of an Urban Street Network［J］.Geoinformatica，2004（2）：157－171.

［4］邓亚娟，杨云峰.基于复杂网络理论的公路网络结构特征［J］.中国公路学报，2010（1）：98－104.

［5］杨 明，高 勇，刘竑冶.基于支持向量机模型的高速公路运营效益评价［J］.系统工程，2009（2）：90－95.

［6］谢洪新，肖 慎.神经网络在高速公路网络综合评价中的应用［J］.公路交通科技，2005（8）：106－110.

［7］刘伟铭，付凌峰.高速公路最佳运营区域划分方法研究［J］.公路交通科技，2008（10）：153－158.

［8］Albert－Laszlo Barabasi.EeicBonabeau.Scale－Free Networks［J］.Scientific American，2003（5）：50－59.

［9］杜 栋，庞庆华.现代综合评价方法与案例精选［M］.北京：清华大学出版社，2005.

［10］郑珞琳，高铁峰.基于AHP与灰色综合评价法的江苏省信息化和工业化发展水平实证分析［J］.情报科学，2011（29）：1217－1220.

［11］陈冬林，黎志成.信息系统投资项目评价指标确定与灰色综合评价［J］.系统工程理论与实践，2002（2）：100－103.

［12］谢洪新，肖 慎.神经网络在高速公路网综合评价中的应用［J］.公路交通科技，2005（8）：106－034.

［13］赵振智，李宏勋.基于多层次灰色综合评价的我国石油公司跨国产权投资方式选择［J］.中国软科学，2009（6）：187－192.