短期聚合理赔总量的平移对数正态分布的近似计算

辛士波

（北京工商大学，北京 100048）

0 引言

记随机变量Ci为某类保单第i次个别理赔额，随机变量N为某个时段（例如一个会计年度）这类保单发生理赔的次数，则短期聚合理赔总量S为:

式中C1,C2,…同分布，N与C1,C2,…独立，当N服从参数为 λ的 Poission分布 P(λ)时称 S服从复合Poission分布。S的数学期望、方差和偏斜度为:

式中 pj(j=1,2,3)是Ci的 j阶原点矩[1]。

关于S的近似，当Ci有偏斜时，文献[2]给出了应用密度函数为g(x-x0;α,β)的平移伽玛分布做近似的方法，式中的α和β是伽玛分布的参数，x0是平移量。x0、α和β与λ和 pj(j=1,2,3)的关系为:

本文选取另一个有偏分布——平移对数正态分布研究S的近似，并对两种近似方法做出比较。

1 平移对数正态分布

1.1 可行性分析

关于S的近似，当Ci有偏斜时，文献[2]给出了应用密度函数为g(x-x0;α,β)的平移伽玛分布做近似的方法，g(x-x0;α,β)中的α和β是伽玛分布的参数，x0是平移量。使用平移伽玛分布近似短期聚合理赔总量的原因在于平移伽玛分布具备右偏特征，且依据近似原理得到的参数估计式简单易算，并没有相关理论研究说明平移伽玛分布近似的效果是最好的，故有理由认为其它具备右偏特征的分布也可以作为S的近似分布。

平移对数正态分布是将对数分布平移后得到的分布，具备了对数正态分布右偏的特征。对数正态分布是非寿险精算中常用的分布，其地位不亚于伽玛分布，其取自然对数变化之后服从正态分布的特征使其地位在某些情况下更优于其它右偏分布，只是对数正态分布的数字特征较伽玛分布复杂，但随着计算机高度发展的今天，使原本复杂的计算变得越来越简单，精度也更加精确。

综述所述，使用平移对数正态分布作为短期聚合理赔总量的近似分布是可行的。

1.2 概率统计性质

平移对数正态分布是将对数分布平移后得到的分布，令随机变量X服从平移对数正态分布，若对数正态分布logN(μ,σ2)的密度函数为 f(x;μ,σ2)[3]，参考平移伽玛分布的记法，记平移对数正态分布为logN(x-x1;μ,σ2)，密度函数为 f(x-x1;μ,σ2)，且其数学表达式为:

（4）式中，f(·)为平移对数正态分布的密度函数，μ、σ2为参数，x1是平移量。

平移对数正态分布logN(x-x1;μ,σ2)的期望、方差及偏斜度见（5）式。

根据平移对数正态分布的性质，服从平移对数正态分布logN(x-x1;μ,σ2)的随机变量X取自然对数之后的lnX应服从平移正态分布，且平移量x1转化为lnx1，而平移正态分布是正态分布平移之后得到，故在logN(x-x1;μ,σ2)平移量x1已知的前提下，可根据转换后的平移正态分布数据进行参数μ和σ2的参数估计和假设检验。

2 近似公式

将（5）式用于S的近似，可得：

（8）式是以λ和 pj(j=1,2,3)为已知，x1、r和t为未知的方程组，在求解t的过程中需要解一元六次方程，注意到因为σ＞0，所以取t＞1。求解（8）式得到 x1、r和t后可依（7）式求得μ和σ2，从而求得LogN(x1,μ,σ2)的全部参数。

3 近似效果对比

设个别理赔额Ci服从指数分布Exp(θ)，所以：

将（9）式代入方程组（8）式的左端，经化简，t（t＞1）由方程：

可求得 x1和r，再依（7）式求得 μ和 σ2。

为对比平移对数正态分布和平移伽玛分布对于S的近似效果，将（9）式代入（3）式，求得平移伽玛分布的参数值为

现取θ=1,2,3,4,5，λ=6，依（10）式计算平移伽玛分布的参数 x0、α和β，依（7）式和（8）式计算平移对数正态分布的参数x1、μ和σ2，计算结果见表1。

依表1的参数值，应用Matlab6.5软件[4]，计算λ=6时不同θ和θ=6时不同λ对应的平移伽玛分布和平移对数正态分布的分布函数值见表2，表2中①表示平移伽玛分布，②表示平移对数正态分布。

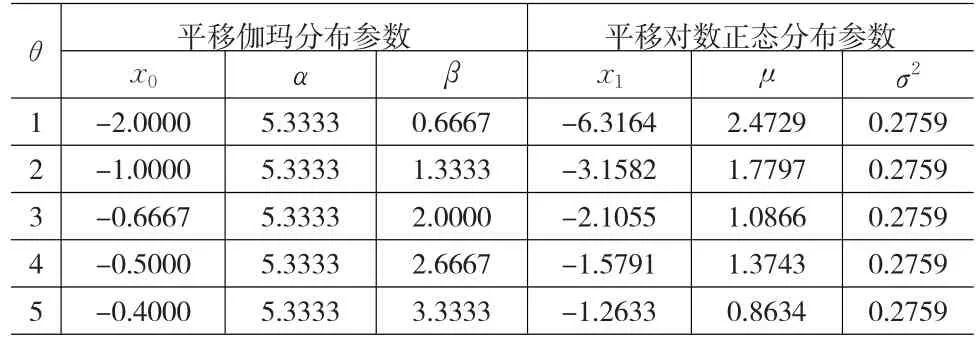
表1 λ=6时不同θ对应的平移伽玛分布参数和平移对数正态分布参数

表2 λ=6时不同θ对应的平移伽玛分布和平移对数正态分布的分布函数值

表2的计算结果说明，短期聚合理赔总量S的平移伽玛分布近似和平移对数正态分布近似的分布函数值差异较小，特别是对于给定的θ，这两个分布的分布函数随着x的增大，越来越接近，表明将对数正态分布用于近似短期聚合理赔总量S具有良好的右尾部近似性质，而且短期聚合理赔总量模型中，右尾部对应的是大额赔付。

4 结论

对于短期聚合理赔总量S的近似，原有的研究结果表明，平移伽玛分布近似是一种有效的近似方法。本文说明，在一定范围内短期聚合理赔总量的平移对数正态分布近似是可行的，进而指出短期聚合理赔总量的平移伽玛分布近似的不唯一。

[1]王晓军,江星,刘文卿.保险精算学[M].北京:人民大学出版社，1995.

[2]谢志刚,韩天雄.风险理论与非寿险精算[M].天津:南开大学出版社，2000.

[3]茆诗松.统计手册[M].北京:科学出版社，2003.

[4]张志涌,徐颜琴.Matlab教程－基于6.x版本[M].北京:北京航空航天大学出版社，2002.