Actigraph（GT3X）加速度计测量我国19～29岁人群身体活动能耗的效度研究

王军利，张 冰，贾丽雅，孙忠伟，郑 尉

1 前言

身体活动（physical activity）是由骨骼肌肉运动产生并伴有能量消耗的任何身体动作；体育锻炼（exercise）则是身体活动的下位概念，是指有计划、有组织、重复实施的，维持或增进身体健康的身体活动［10］。身体活动量与健康的剂量-效应关系已得到流行病学研究的证实［16］。因此，如何能够客观、准确、有效地测量身体活动量及其能量消耗显得尤为重要。

Actigraph加速度计作为领域内应用最为广泛的同类产品之一，不仅可以监测日常身体活动量、强度以及活动方式，还能够评价人体运动的能量消耗。已经被65个国家或地区的1500多所院校与科研机构使用，同时得到直接与间接测热法、双标水法（DLW）的效度验证［3］。尽管不同类型加速度计在监测身体活动时的效果比较相似［27］，但是，各自的动作计数切割点与能耗算法方程的准确性并不一样［32］。因为，建立在不同运动方式与人种基础上的能量推算方程，预测精度存在较大的差别［1］。加速度计的动作计数与梅脱强度依赖于建模的动作类型，基于不同类型活动建立起来的加速度计算法方程，测量其他动作类型的身体 活 动 能 耗 时 可 能 存 在 低 估 或 者 高 估 的 现 象［7，18，20，23］。 此外，加速度计也存在一个上限效应。研究显示，当运动强度超过10梅脱时，加速度计明显会低估实际的能量消耗［15，21］。不仅如此，还有研究认为，加速度计并不能够有效地测量人体的各种身体活动，无论是低强度、中等强度还是剧烈强度的活动［12］。鉴于此，Actigraph（GT3X）加速度计对我国人口群体的适用性仍未可知，且国内的研究也较少见。于是，本研究在实验室条件下，通过运动跑台上不同速度的走跑运动与佩戴测试，对Actigraph（GT3X）加速度计的能耗算法方程进行有效性验证研究，可为国内的研究人员与普通大众使用三轴加速度计提供有益的参考。

2 研究方法

2.1 受试对象

研究的受试者为年轻成年人（表1），主要包括在校的本科生、硕士生、博士生。受试者基本上有锻炼的经历或者运动习惯，身体健康，无运动禁忌症。

表1 本研究测试对象的人体测量特征一览表Table 1 The Anthropometry Characteristics of Participants （D）

表1 本研究测试对象的人体测量特征一览表Table 1 The Anthropometry Characteristics of Participants （D）

n年龄（岁） 身高（cm） 体重（kg） 体脂 （%）男性女性合计1462025.5±1.622.6±1.224.7±5.3173.4±1.3164.1±2.2170.6±6.568.8±2.951.8±2.063.7±12.219.9±1.022.7±0.920.8±3.6

2.2 测试仪器与程序

2.2.1 GT3X加速度计

GT3X由美国制造技术有限公司（Manufacturing Technology，Inc，MTI）生产，是一款三轴加速度计，具有动作计数、计步、能量消耗、活动强度水平、代谢当量（METs即梅脱）、睡眠分析等监测与分析功能。该工具使用方便，数据过滤及数据抽样间隔设置可以在采集后执行，因而，用户能够按照需要进行数据分析。ActiGraph ActiLife 6.1.4是测试数据处理的专用软件，该软件能够将测试数据下载到计算机终端。打开并运行程序后，选择相应的参数设置，计算机将自动分析运动过程中的步数、运动能耗、活动时间、强度水平等指标结果。ActiGraph ActiLife 6.1.4软件内置有5个适合成年人（适用于19岁以上人群）的运动能耗算法方程，即 Williams work-energy（WW）方程、Freedson（F）方 程、Freedson Combination（FC）方 程、Freedson VM3（VM3）方 程 以 及 Freedson VM3Combination（VM3C）方程［4］（表2）。其中的联合方程采用了分段计算能量消耗的方法，可以精确计算不同强度水平的身体活动能耗值。

文献资料显示，佩戴加速度计最合适的位置是腰髋部位［2，19，27，29］，这 是 因 为 其 更 接 近 人 体 的 质 心 ，能 够 监 测 到 整体运动姿态的人体运动参数，避免局部运动导致的身体活动能耗监测失真现象。为了获得有效的测量结果，本研究将GT3X加速度计佩戴在受试者的左后侧腰部（与髂嵴上缘齐平）。佩戴与测试前，需要ActiGraph ActiLife 6.1.4专用软件的初始化操作。测试结束后立即取下装置，通过专用软件将数据信息下载到电脑。依据动作计数曲线图对5个速度水平的时间段进行截取处理（图1），图中的5个波段代表5个运动速度阶段，由此计算出受试者不同运动强度时的能量消耗情况。

2.2.2 运动跑台与 MAX-Ⅱ心肺功能仪

为了保证运动强度的精确控制，本研究选择的运动跑台为h／p／cosmos公司（德国）生产的Pulsar专业级运动跑台。其主要技术参数为:跑带面积（190×65cm2）、可选速度（0～40km／h）、可调坡度（±25%），并配有保护支架、拱形支架、减重支架等以保护受试者的安全［19］。依据国内、外同类实验的研究设计，普通人群的测试运动强度一般控制在轻度到剧烈强度水平，最为常见的运动速度范围是3～10km／h之间，每个运动速度的持续时间也多为3～10min［12，13，18，21，28，30，31］。通常认为 ，2～3.9梅脱为轻度活动水平，4～5.9梅脱为中等强度活动水平，6梅脱以上为高强度运动［11］。考虑到日常身体活动强度的变化范围，本实验选择的测试速度是4km／h、5.6km／h、6.4km／h、7.2 km／h以及8km／h速度水平的走跑运动，分别相当于3梅脱、4.3梅脱、5.5梅脱、7梅脱、8.5梅脱的运动强度水平［6］，基本包括了轻微至剧烈的运动强度水平。同时，为了确保受试者能够顺利完成测试，并获得有效的数据，要求每个强度必须持续运动 5min［14，18，21，22，28］。此外，运动 前还要进行3～5min的热身，测试中受试者可依据自己的运动能力，自主选择走或者跑的运动方式。

加速度计测量效度的验证研究中，运动能量消耗的效标值多采用间接测热法。该方法主要是通过一口气接一口气的呼吸装置，精确计算人体运动能量消耗。目前，便携 式的间接测热系统是常用的方法手段［8，12，17，20，23，25，28，30］，本研究应用的MAX-II型心肺功能测试系统（美国AEI公司生产）具有同样的测试原理与功能，因为不方便携带，只能应用于实验室的测试，在个别研究测试中也有使用［2］。受试者佩戴专用面罩，仪器可以测出呼吸时氧气的消耗和二氧化碳的量，系统将自动计算运动时的能量消耗，测试时由专门的实验人员现场（馆）记录。实验测试前，首先对仪器进行标准气体标定，然后完成气筒标定，其误差范围为±1之间，测试将在室温20°左右与空气相对湿度为45%的条件下完成［26］。

2.2.3 其他测试准备

采用标准的身高计与体重计测试受试者的身高与体重，精确度分别为0.1cm和0.1kg，测量时要求受试者赤脚并穿尽量少的衣服。此外，测试前受试者还要填写知情同意书，了解测试的细节与具体要求，以保证测试的顺利完成。

2.2.4 数据统计

利用数据分析处理软件SPSS 17.0对5个算法方程计算的能耗值与间接测热法的能耗值进行Pearson相关分析、方差分析、配对t检验分析，结合Bland-Altman点图分析各算法方程的效度水平。此外，利用单因素方差分析与组内相关分析（ICC）对不同能耗算法方程之间的一致性进行比较分析。

3 结果与分析

3.1 各算法方程预测能耗的效度

不同算法方程预测能耗的统计结果（表3）显示，随着速度的增加，测量值的标准差增大，但5.6km／h时除外。在效度水平检验方面（表4），通过算法方程的预测值与间接测热法之间的相关分析与配对t检验进行分析。在4 km／h的运动速度时，VM3C、VM3、F、FC、WW 等5个方程的预测值与间接测热法之间都具有显著的相关性，r范围在0.66～0.97之间；但配对t检验结果均具有显著性差异，t值范围在-2.15～-4.68之间，其中，F方程的P≤0.05，其他方程的P≤0.01。在速度为5.6km／h时，5个方程与间接测热法的相关性显著（r＝0.67～0.75之间），而配对t检验结果均无显著性差异（P≥0.05）。当速度增加到6.4km／h时，5个方程的预测值与间接测热法同样具有显著性相关（r＝0.66～0.82之间），配对t检验结果显示，只有VM3C、WW方程差异性不显著，且t值分别为-1.98和0.08，P 值分别为0.06和0.93。当速度达到7.2km／h和8km／h的时候，5个方程与间接测热法的相关性有所提高，r范围分别为0.87～0.89之间和0.83～0.97之间，惟有 WW 方程（7.2km／h的运动强度时）的配对t检验没有显著性差异（P＝0.07），其他方程的t检验结果均表现出了显著性差异。

为了了解方程预测能耗值的误差大小，算法方程计算的能耗值减去测热法的能耗值，然后除以测热法的能耗值并乘以100表示各能耗方程预测的误差。对各能耗方程在不同速度水平的误差大小进行算术平均后发现（图2），多数方程预测的能耗值都低于间接测热法的能耗值，只有WW方程在6.4km／h的速度时为高估。5个能耗方程在4km／h与6.4km／h的速度时，能耗预测值的差异性最大，表5的数据也显示出同样的趋势。但是，在5.6km／h的速度时，各能耗方程的效度最好。

表3 本研究间接测热法与5个算法方程的测量结果一览表Table 3 The Measurement Results of Indirect Calorimetry and Five Algorithm Equation （D）

表3 本研究间接测热法与5个算法方程的测量结果一览表Table 3 The Measurement Results of Indirect Calorimetry and Five Algorithm Equation （D）

注:VM3C代表Freedson VC3Combination（2011）方程；VM3代表Freedson VM3（2011）方程；F代表Freedson（1998）方程；FC代表Freedson Combination（1998）方程；WW 代表 Williams work-energy（1998）方程。

VM3C（kcal） VM3（kcal） F（kcal） FC（kcal） WW（kcal） 间接测热法（kcal）4km／h 19.93±7.83 18.28±8.45 19.49±10.23 21.63±11.15 19.93±7.61 25.14±7.185.6km／h 32.79±8.82 32.00±9.65 32.37±11.68 32.76±10.31 34.10±6.35 34.24±6.356.4km／h 42.86±11.93 42.47±12.26 41.16±13.69 41.75±13.42 46.52±14.62 46.31±10.697.2km／h 49.25±17.08 48.44±17.36 45.36±18.47 46.20±18.25 51.15±21.22 55.87±20.478km／h 44.54±23.11 43.70±22.47 41.06±22.48 41.72±23.20 47.82±26.93 53.86±30.21合计 188.40±56.34 184.88±56.82 180.11±67.31 184.08±67.24 198.07±70.24 215.41±66.30

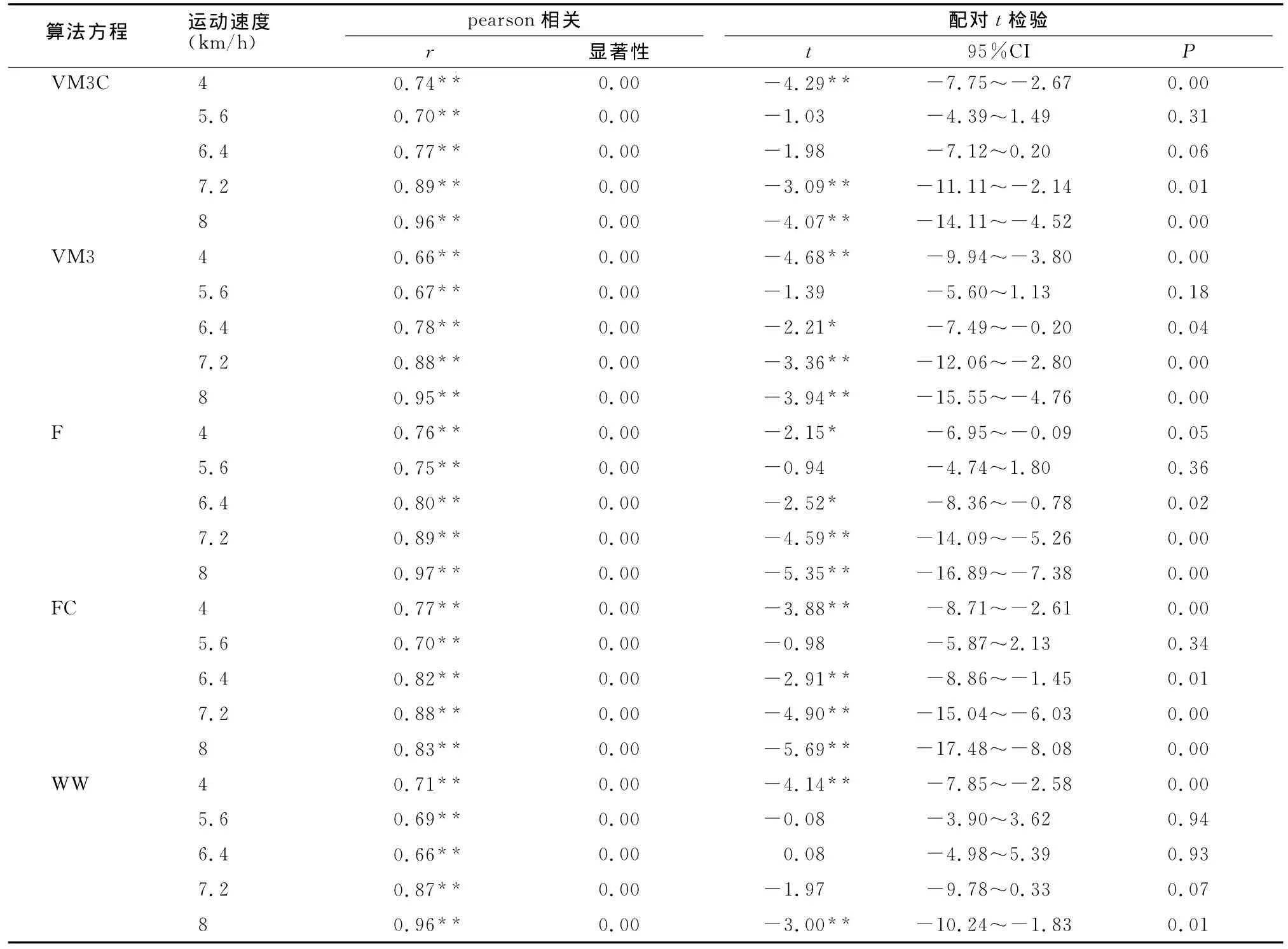
表4 本研究在不同速度时各能耗算法方程的效度比较一览表Table 4 The Validity of Every Algorithm at Different Speed

图2 本研究不同速度时各方程预测值误差均值比较示意图Figure 2.The Average Level of Prediction Error of Each Equation at Different Speed

3.2 不同算法方程预测能耗的一致性

单因素的方差分析结果发现（表5），在不同速度时，各算法方程预测的能耗值具有较好的一致性。但是，算法方程的一致性水平存在运动速度上的差异，在以4km／h、5.6km／h、6.4km／h、7.2km／h、8km／h的速度运动时，方差分析的P 值分别为0.85、0.98、0.73、0.86、0.91、0.92，均没有显著性差异出现。尤其是在5.6km／h的速度情况运动，算法方程的能耗值一致性最高，但是，以6.4km／h的速度运动时，方程之间的能耗预测差异最大。

组内相关（ICC）系数分析的结果显示（表5），VM3C、VM3、F、FC、WW等5个方程在不同速度的能耗预测值都具有较高的组内相关。在以4km／h、5.6km／h、6.4km／h、7.2km／h、8km／h的速度运动时，方程间的科隆巴赫系数（α值）分别在0.98、0.99、0.99、0.99、0.99，说明不同算法方程的运动能耗结果具有很好的一致性。上述两种方法的分析结果发现，各算法方程的总能耗具有同样好的一致性。

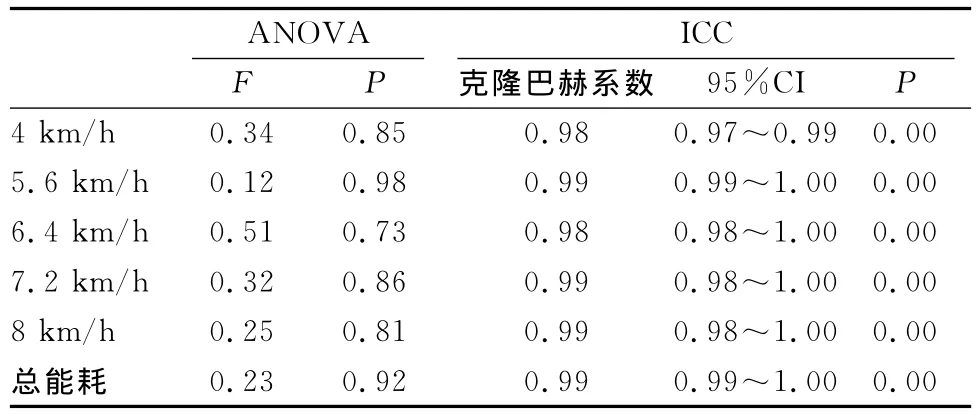
表5 本研究5个算法方程预测值一致性一览表Table 5 The Consistency of Five Algorithm Equation Prediction Value

4 讨论与分析

4.1 各算法方程预测能耗的信效度分析

通过对能耗方程与间接测热法的Pearson相关分析，发现5个能耗算法方程均具有显著的相关（P≤0.01）。但通过与间接测热法的配对t检验，两种方法并不是在所有运动强度时都保持较好的一致性，且在较高运动强度时这种不一致性有增大的趋势。也表明随着速度的增大，加速度计的测量效度有下降的趋势。其中，只有WW方程在6.4km／h的速度时，t＞0，表示该方程预测的能耗均值大于间接测热法的能耗均值，即处于高估水平；而其他方程在任何速度水平上的t值都为负值，即能耗值为低估水平。只有在5.6km／h的速度时，t值变化的绝对值最小，算法方程最接近间接测热法的能耗值。此外，VM3C、VM3、F、FC等4个方程在5.6km／h与6.4km／h的t值最为接近，表明在这2个速度时4个方程的预测水平比较接近。

由于不同的能耗方程在三维方向上的动作计数采取不同的切割点，有的方程还采用了分段计算的方法以提高能耗预测的准确性。其中，WW方程是利用能量守恒的原理，总动作数的多少是人体运动做功大小的重要参数；F方程与VM3方程分别评估单位时间动作数在1952和2453之上时的能耗值；FC与VM3C则采用了分段计算的方法，同时，预测动作数低于或高于1952和2453时的能耗值［3］。但是，本研究中所有5个方程的能耗值都是随着速度的增加误差先减小然后逐渐增大，这可能与受试者的运动方式有关［7，18，20，23］。因为，对于不同的受试者而言，同样的运动速度则意味着不同的运动强度。4km／h、5.6 km／h、6.4km／h、7.2km／h、8km／h的速度水平相对应的运动强度分别为3梅脱、4.3梅脱、5.5梅脱、7梅脱和8.5梅脱［6］，当在较低速度（或者强度）运动时，多数受试者都可以轻松地步行。当达到5.6km／h与6.4km／h的中等强度水平时，受试者的运动能力决定了走跑兼用的变化方式，导致有效的动作计数明显增加。而跑步时的恒定垂直加速度可能影响加速度计的动作数，较高的运动速度时某些有效数据甚至会被过滤掉，以至于会导致能耗预测值低估［9］。

t值的正负表示预测值的高估与低估，其变化区间的绝对值大小也反映了预测误差的变化大小。VM3C、VM3、F、FC、WW 等5个方程的t值变化区间分别为-4.29～-1.03、-4.68～-1.39、-5.35～ -0.94、-5.69～-0.98、-4.14～0.08。可以发现，与间接测热法差值的稳定程度高低依次是VM3C、VM3、WW、F、FC。从测量结果的整体情况看，随运动强度的增加，WW算法方程的能耗值先是低估然后接近效标值，再从高估转变为低估（图2）。尽管其能耗预测的平均误差水平较低（图3），但有可能导致不良的系统误差水平。如果个体经常从事5梅脱强度左右的身体活动，WW算法方程的结果会出现高估现象，而从事其他运动强度的个体会出现相反的结果。人们日常的身体活动中包括了家务的、工作的、锻炼的以及交通等多样化的身体活动方式，且具体活动情况会因人而异，有可能会导致某种情况下一直低估或者一直高估的两极化现象，所以，该能耗方程并不是最合适的。虽然VM3C算法方程总体上一直处于低估水平，但具有较稳定与较低的系统误差水平。目前，多数加速度计的算法方程都是基于实验室条件下的跑台运动获得的。研究发现，其预测日常身体活动能耗时会存在低估或者高估的问题［5，18，22，31］。但是，考虑到人们日常身体活动方式的多样性，具有较好系统误差水平的能耗方程才能够准确地评价人体运动的能量消耗，并适用于个体间的运动能耗比较。研究结果认为，VM3C方程是比较合适的耗算法方程。

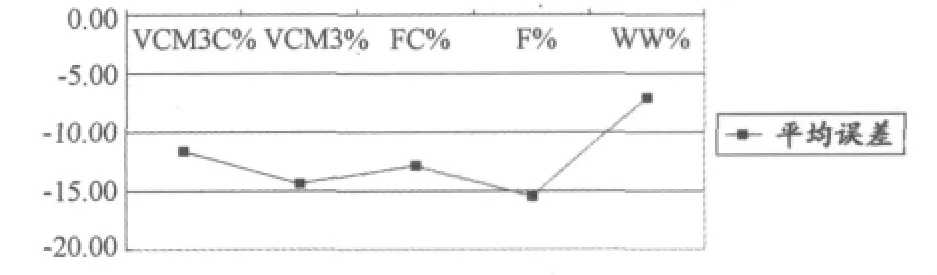
图3 本研究各算法方程预测能耗的平均误差示意图Figure 3.The Average Error of Predicting Energy Expenditure of Each Algorithm

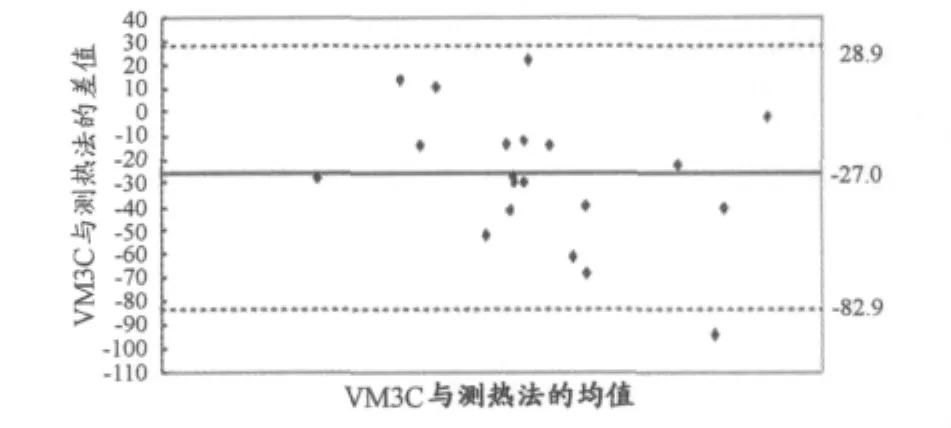
图4 本研究VM3C算法方程总能耗值的Bland-Altman散点图Figure 4.The Bland-Altman Plot of Total Energy Expenditure Value of VM3CAlgorithm Equation

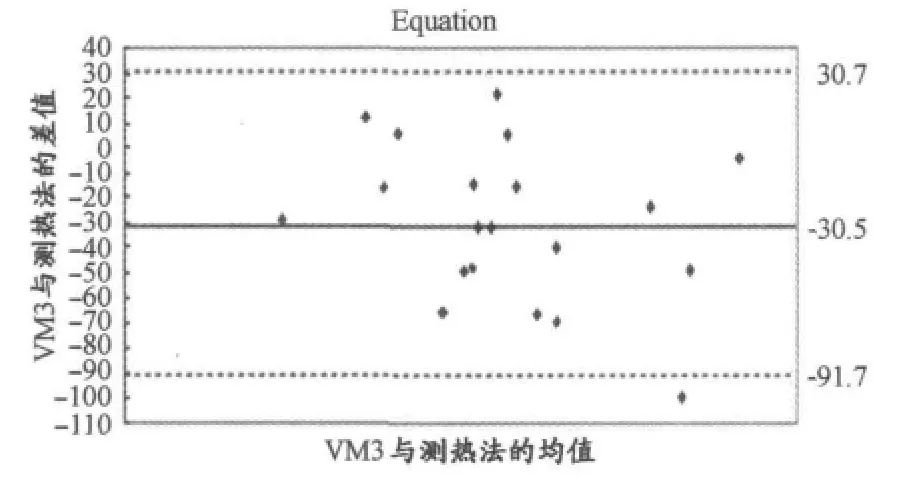
图5 本研究VM3算法方程总能耗值的Bland-Altman散点图Figure 5.The Bland-Altman Plot of Total Energy Expenditure Value of VM3Algorithm Equation

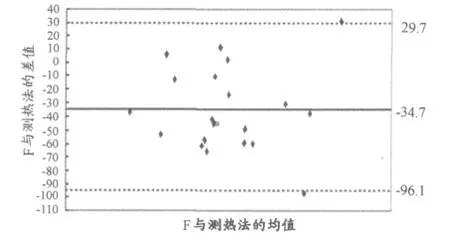
图6 本研究F算法方程总能耗值的Bland-Altman散点图Figure 6.The Bland-Altman Plot of Total Energy Expenditure Value of F Algorithm Equation

图7 本研究FC算法方程总能耗值的Bland-Altman散点图Figure 7.The Bland-Altman Plot of Total Energy Expenditure Value of FC Algorithm Equation

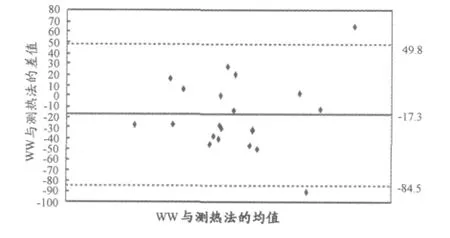
图8 本研究WW算法方程总能耗值的Bland-Altman散点图Figure 8.The Bland-Altman Plot of Total Energy Expenditure Value of WW Algorithm Equation

尽管各个算法方程的误差程度存在差异，似乎不会影响方程预测能耗值与间接测热法之间的相关水平，却能够影响二者的一致性［24］。因此，本研究试图通过对5个算法方程预测的总能耗值进行Bland-Altman点分析方法（图4～图8），对算法方程与间接测热法的一致性进一步探讨。图中，X轴为算法方程与间接测热法能耗值和的均值，Y轴为算法方程与间接测热法能耗值的差值，2条虚线表示Mean±1.96SD，即为2种能耗预测方法差值的95%置信区间范围，而中间的实线表示2种方法差值的均值。结果发现，VM3C、VM3、F、FC、WW 与间接测热法的差值在95%一致性界限外的点数分别为5%、5%、10%、10%、10%，都在可接受的范围。差值的实际均值与理论均值（即为Y轴的0刻度值）之间的距离表示预测偏倚程度，其偏倚度依次是-27.0、-30.5、-34.7、-31.0、-17.3，且一致性界限内差值的最大绝对值分别为67.9、69.3、65.8、57.8、50.7。总能耗的 Bland-Altman点分析结果发现，在算法方程与间接测热法的一致性上，似乎并没有一个算法方程达到理想水平。但理论上认为能耗预测的偏倚度、一致性界限内的最大差值、一致性界限外的点数愈小愈好，而目前学界也没有明确的判定标准。相比较而言，WW与VM3C两个方程和间接测热法的一致性水平较好。综合前述分析后认为，在5个方程中，VM3C方程预测人体运动能耗的效度更好。

4.2 不同算法方程测量运动能耗的一致性分析

对5个方程进行单因素的方差分析后发现，在所有的速度水平上，算法方程之间的一致性较好。其中，单因素方差分析的显著性水平最低值为0.73，表明方程间均没有显著性差异（P≥0.05）。而在5.6km／h时的显著性水平达到0.98，说明5个方程几乎没有差异。在以5.6km／h、8km／h、7.2km／h、4km／h、6.4km／h的速度运动时，显著性特征值依次是0.98、0.91、0.86、0.85、0.73。在5.6km／h与8km／h速度水平运动时，5个算法方程的一致性是相对最大的，图3也显示同样的趋势。结合组内相关系数（ICC）的分析结果，发现所有的能耗方程的组内相关系数都在0.9以上，除4km／h的速度以外，其他运动强度下的组内相关系数都高于0.99，充分说明各能耗方程具有较高的一致性水平。因此，如果个体以较低的运动强度进行身体活动时，尤其是在4.3梅脱（5.6km／h）时，各算法方程间具有可替代性，但其他运动强度时仍需要谨慎地选择使用。

5 结论与建议

GT3X加速度计的各能耗算法方程与间接测热法之间具有较高的相关性，但可靠性水平存在运动强度上的差异。与其他研究结果一致，加速度计测量人体运动能耗时会存在低估或者高估的现象。但本研究中，只有WW能耗方程出现了高估的现象，其他4个方程一直保持低估水平。5个能耗算法方程在较低速度（4km／h以下）与较高速度（7.2km／h以上）时，具有较大的测量误差，而且方程间的一致性也较低。相比较而言，VM3C方程的系统误差较小且稳定，是最为合适的能耗算法方程。

Actigraph（GT3X）加速度计作为高技术含量的客观测量手段，在实验条件下测量我国年轻人群体的运动能耗是可行的，但用于日常生活中身体活动的能耗监测尚需进一步验证研究。此外，研究没有对运动强度、量、步数等功能进行定性和定量评价，同时，是否适用于我国的其他人群仍需要进一步探讨。

［1］汤强，盛蕾，朱卫红.体力活动研究中加速度计的应用［J］.体育科学，2009，29（1）:77-84.

［2］赵壮壮，陈培友，邱悦雯.LivePod LP2检测人体运动中能量消耗水平的信、效度检验［J］.体育科学，2012，32（1）:48-53.

［3］ActiGraph GT3XHelp［EB／OL］.http:／／support.theactigraph.com／product／GT3X-device.

［4］ActiGraph Monitor［EB／OL］.http:／／www.theactigraph.com／article／research-database.

［5］AINSLIE P N，REILLY T，WESTERTERP K R.Estimating human energy expenditure-A review of techniques with particular reference to doubly labeled water［J］.Sports Med，2003，33（9）:683-698.

［6］AINSWORTH B E，HASHELL W L，HEMMANN S D，et al.2011compendium of physical activities:a second update of codes and MET values［J］.Med Sci Sports Exe，2011，43（8）:1575-1581.

［7］BASSETT JR D R，AINSWORTH B E，SWARTZ A M，et al.Validity of four motion sensors in measuring moderate intensity physical activity［J］.Med Sci Sports Exe，2000，32（9Suppl）:S471-S480.

［8］BRAGE S，BRAGE N，FRANKS P W，et al.Reliability and validity of the combined heart rate and movement sensor Actiheart［J］.Eur J Clin Nutrit，2005，59（4）:561-570.

［9］BRAGE S，WEDDERKOPP N，FRANKS P W，et al.Reexamination of validity and reliability of the CSA monitor in walking and running［J］.Med Sci Sports Exe，2003，35（8）:1447-1454.

［10］CASPERSEN C J，POWELL K E，CHRISTENSON G M.Physical activity，exercise，and physical fitness:definitions and distinctions for health-related research［J］.Public Health Reports，1985，100（2）:126-131.

［11］COMMITTEE P A G A.Physical activity guidelines advisory committee report，2008［M］.Washington，DC:US Department of Health and Human Services，2008.

［12］CROUTER S E，CHURILLA J R，BASSETT D R.Estimating energy expenditure using accelerometers［J］.Eur J Appl Physiol，2006，98（6）:601-612.

［13］CROUTER S E，CLOWERS K G，BASSETT D R.A novel method for using accelerometer data to predict energy expenditure［J］.J Appl Physiol，2006，100（4）:1324-1331.

［14］CROUTER S E，SCHNEIDER P L，KARABULUT M，et al.Validity of 10electronic pedometers for measuring steps，distance，and energy cost［J］.Med Sci Sports Exe，2003，35（8）:1455-1460.

［15］DRENNOWATZ C，EISENMANN J C.Validation of the SenseWear Armband at high intensity exercise［J／OL］.Eur J Appl Physiol，DOI:10.1007／s00421-010-1695-0.

［16］GENERAL U S P H，FITNESS P C O P，Us S.Physical activity and health:a report of the Surgeon General［M］.Jones Bartlett Pub，1998.

［17］HEIL D P.Predicting activity energy expenditure using the Actical activity monitor［J］.Res Q Exe Sport，2006，77（1）:64-80.

［18］HENDELMAN D，MILLER K，BAGGETT C，et al.Validity of accelerometry for the assessment of moderate intensity physical activity in the field［J］.Med Sci Sports Exe，2000，32（9）:S442-S449.

［19］H／P／COSMOS.pulsar Running machines manual［EB／OL］.http:／／www.h-p-cosmos.com／en／running-machines／pulsar／index.htm.

［20］JAKICIC J M，MARCUS M，GALLAGHER K I，et al.Evaluation of the SenseWear Pro Armband（TM）to Assess Energy Expenditure during Exercise［J］.Med Sci Sports Exe，2004，36（5）:897-904.

［21］KOEHLER K，BRAUN H，de MAR？ES M，et al.Assessing energy expenditure in male endurance athletes:Validity of the Sensewear Armband［J］.Med Sci Sports Exe，2011，43（7）:1328-1333.

［22］LEEDERS N Y，NELSON T E，SHERMAN W M.Ability of different physical activity monitors to detect movement during treadmill walking［J］.Int J Sports Med，2003，24（1）:43-50.

［23］LE MASURIER G U Y C，TUDOR-LOCKE C.Comparison of pedometer and accelerometer accuracy under controlled conditions［J］.Med Sci Sports Exe，2003，35（5）:867-871.

［24］MARTIN BLAND J，ALTMAN D G.Statistical methods for assessing agreement between two methods of clinical measurement［J］.The Lancet，1986，327（8476）:307-310.

［25］MATTHEWS C E.Calibration of accelerometer output for adults［J］.Med Sci Sports Exe，2005，37（11）:S512-S522.

［26］MAX-II／ MAX-IIa Metabolic Systems Instruction Manual［EB／OL］.http:／／www.aeitechnologies.com.

［27］MCCLAIN J J M C，CRAIG C L C C，SISSON S B S S，et al.Comparison of Lifecorder EX and ActiGraph accelerometers under free-living conditions［J］.Appl Physio Nutrit Metabol，2007，32（4）:753-761.

［28］NICHOLS J F，MORGAN C G，SARKIN J A，et al.Validity，reliability，and calibration of the Tritrac accelerometer as a measure of physical activity［J］.Med Sci Sports Exe，1999，31（6）:908-912.

［29］TROST S G，MCIVER K L，PATE R R.Conducting accelerometer-based activity assessments in field-based research［J］.Med Sci Sports Exe，2005，37（11）:S531-S543.

［30］VANHELST J，BÉGHIN L，RASOAMANANA P，et al.Calibration of the RT3accelerometer for various patterns of physical activity in children and adolescents［J］.J Sports Sci，2010，28（4）:381-387.

［31］WELK G J，BLAIR S N，WOOD K，et al.A comparative evaluation of three accelerometry-based physical activity monitors［J］.Med Sci Sports Exe，2000，32（9Suppl）:S489-S497.

［32］WELK G J，MCCLAIN J J，EISENMANN J C，et al.Field Validation of the MTI Actigraph and BodyMedia Armband Monitor Using the IDEEA Monitor［J］.Obesity，2007，15（4）:918-928.