二进制和多进制LDPC编码调制系统的带宽有效传输＊

赵 菲 杨春顺

（1.海司信息化部 北京 100036）（2.海军驻上海地区军事通信代表室 上海 200333）

1 引言

1962年Gallager在他的博士论文中首次提出了LDPC码［1］，并在论文中提出了两种递归概率译码算法。但是由于当时计算机运算能力水平的限制，未能证明其具有接近Shannon限的能力，同时也没有给出译码算法严格的性能界线，高复杂度也使得LDPC码编译码器难以硬件实现，当时被认为是一种不实用码。但是Gallager提出了两个具有创造性的观点［1］：1）用简单稀疏校验矩阵的随机置换和级联来模拟随机码；2）采用迭代译码的方法逼近最大似然译码。由于当时RS码和卷积码的级联被认为非常适于实际的差错控制系统，致使Gallager的工作被忽视了近30年，在这沉寂的30年期间，Zyablov、Pinsker、Margulis以及Tanner仍然还致力于LDPC码的研究［2］。直到Turbo码的提出以后，人们才发现Turbo码实质上就是LDPC码的一个特例，LDPC码又重新燃起了人们的兴趣。1996年，Mackay等人的研究使LDPC码的研究跨入了一个新阶段［3］，他指出LDPC码可以像Turbo码一样接近Shannon限。1998年，Davey和Mackay重新发现了多进制LDPC码［4］，提 出 了 用 于 译 码 的 多 进 制 和 积 算 法 （Q－ary Sum－Product Algorithm，QSPA），相比于二进制LDPC码来说取得了明显的编码增益，多进制LDPC码的出现为LDPC码的研究开拓了一个全新的领域。多进制LDPC码除具备LDPC码的一般特性外，还具有以下独特优势［7］：1）更好的纠错能力；2）抗突发错误能力强；3）适合高速率传输系统。

近年来无线通信的迅速发展以及带宽资源的不断受限，研究的信道编码方案不仅要求具有功率有效性，而且同时要求具有频带有效性，这一迫切要求使得编码调制技术成为近年来研究工作的热点。编码调制结合的思想是将信道编码同调制技术联合考虑，通过对信号空间分配，来最大化信号相点间的最小欧氏距离，以达到抗干扰的目的。先进的编码和高效的调制技术相结合可找到功率利用率和频带利用率之间的一个最佳平衡点。由于LDPC－BICM技术具有良好的应用前景，必将被广泛地应用到通信中的各个领域。因此，研究多进制LDPC－BICM系统是多进制LDPC码应用研究的一个方向。多进制LDPC－BICM系统可以获得更好的纠错性能，码字自身的内在交织性可完成各信息符号之间的交织，能达到更高的数据传输速率和频谱效率。本文主要研究多进制LDPC－BICM的编码调制系统在带宽有效传输下的性能。首先建立了多进制LDPC－BICM系统，分析了在AWGN信道下不同编码调制结合的译码初始化条件，最后给出了仿真结果和分析。

2 系统模型

LDPC码的编码调制系统主要有两个方向：一个是多级编码调制（MultiLevel Coding，MLC）；另一个是比特交织码调制（Bit Interleaved Coded Modulation，BICM）。以上两种系统都是基于高阶调制的，两者的区别在于BICM只需要一个编译码器，而MLC需要采用多个编译码器，考虑系统的复杂性，本文主要研究多进制LDPC－BICM系统。为了减少系统的复杂度，传统的编码调制系统在编译码与调制解调之间需要交织与解交织器，由于LDPC码校验矩阵中非零值的随机分布特性及其高度稀疏性，使LDPC码本身具有内在交织性。这些特性使得多进制LDPC码编码的同时，也完成了各信息符号之间的交织，因此，构造多进制LDPC码编码调制系统时，可省略交织与解交织器，从而降低系统的复杂度并缩短了时延。多进制LDPC－BICM编码调制系统如图1所示。当采用q进制LDPC码与M阶调制匹配结合（M＝q）的编码调制方式，可以提供更高的数据传输速率和频谱效率，有利于带宽有效传输，同时可以避免发送端和接收端比特与符号之间软信息转换。当LDPC码的进制数q与调制阶数M不匹配时，就需要进行二进制与多进制译码软信息的转换，下节将详细讨论分析软信息的转换问题。

图1 多进制LDPC编码调制系统框图

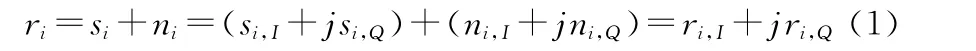
其中，ni，I、ni，Q为两个独立同分布均值为零方差为σ2的高斯白噪声。

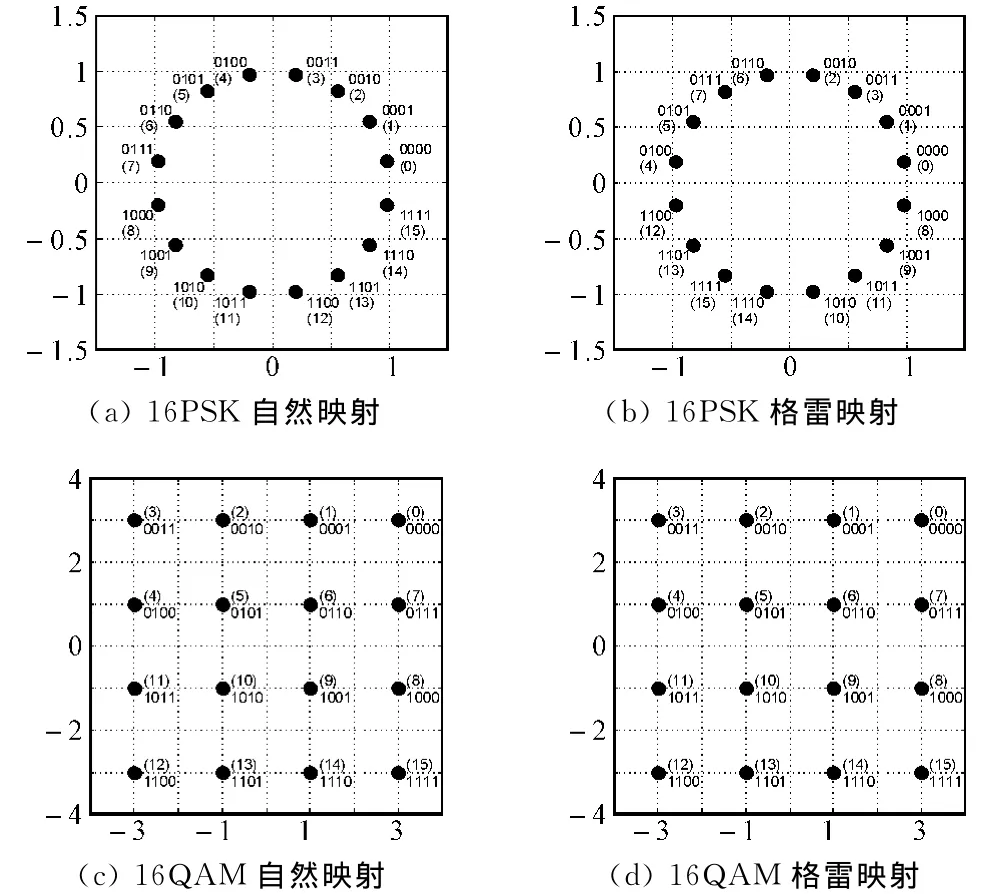
图2 不同调制下方式下的映射图

3 初始化译码信息

本节重点研究不同LDPC编码调制组合初始译码信息的计算。当LDPC码的进制数与调制方式阶数匹配时，对于高阶调制的二维信号，接收向量ri，I、ri，Q的联合概率密度为

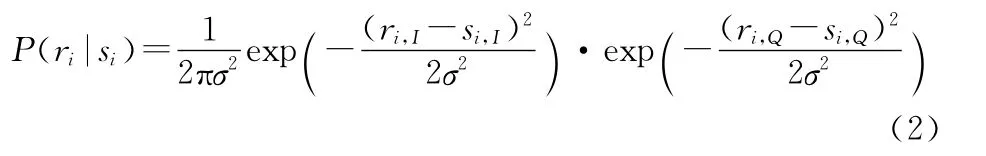
假设发送各符号的先验概率相等，则后验概率为

当LDPC码的进制数与调制方式阶数不匹配时，通常存在两种情况：1）多进制LDPC码与BPSK调制结合；2）二进制LDPC码与高阶调制结合。这两种情况在译码初始化时分别存在二进制软信息转化为多进制软信息和多进制软信息转化为二进制软信息的问题。

对于情况1），每个二进制比特的置信概率如式（4）所示。由于信道是无记忆的，根据二进制置信信息，符号的置信概率为

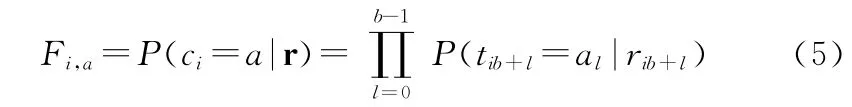
其中，tib＋l∈｛－1，1｝为码字ci的双极性表示，al∈｛－1，1｝对应于tib＋1的取值，0≤l≤b－1，q＝2b。

由式（5）得到的Fi，a可作为多进制LDPC码迭代译码的初始化概率值。

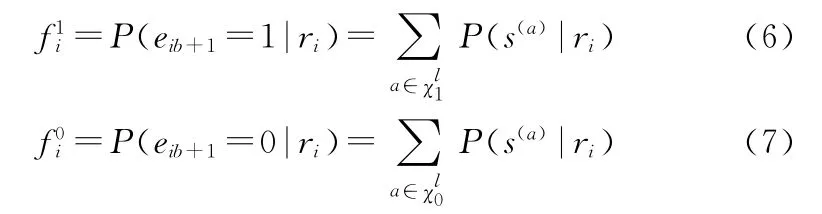
4 仿真实验及性能分析

本节对多进制和二进制LDPC编码调制系统在AWGN信道下进行了性能仿真和比较分析。仿真的LDPC码都选用结构化的QC LDPC码。多进制LDPC码的迭代译码采用FFT－QSPA算法，二进制LDPC码译码采用SPA算法，最大迭代次数都设置为50。

首先考查多进制LDPC－BICM系统与二进制LDPCBICM系统的对比情况。选用有限域第I类构造方法构造出同比特长度同码率的多进制和二进制LDPC码。16进制（225，173）LDPC码采用基于GF（24）域的有限域第I类构造方法，其校验矩阵H为60×255大小的矩阵，由具有15×15循环置换矩阵的4×15阵列构成，列重行重分别为4和14。二进制（899，691）LDPC码采用基于 GF（25）域的有限域第I类构造方法，其校验矩阵H为403×899大小的矩阵，由具有31×31循环置换矩阵的13×29阵列构成，列重行重分别为13和28。采用16PSK调制方式，16进制LDPC－BICM系统和二进制LDPC－BICM系统在AWGN信道下的误码性能曲线和平均迭代性能曲线分别如图3和图4所示。在FER为10－4处，多进制LDPC－BICM系统较二进制LDPC－BICM系统取得了大约10dB的编码增益，对比仿真结果说明了多进制LDPC码与高阶调制结合的优势。

对码率为0.5的16－ary（120，60）QC LDPC码，其校验矩阵为60×120大小的矩阵，由具有15×15循环置换矩阵的4×8阵列构成，其秩为60，列重行重分别为3和6。图5给出了在AWGN信道下该码采用16QAM和16PSK调制方式、自然映射和格雷映射的误码率曲线图，图6给出了对应的平均迭代次数曲线图。从图5和图6可以看出，采用16QAM调制方式比16PSK具有更好的误码和迭代性能。在FER为10－4处，AWGN信道下采用16QAM格雷映射方式相比于16PSK格雷映射取得了大约2.22dB的编码增益；在5dB处，16PSK格雷映射方式的迭代次数是16QAM格雷映射的6.7倍。

图3 16进制（225，173）LDPC码和二进制（899，691）LDPC码编码调制系统的误码性能

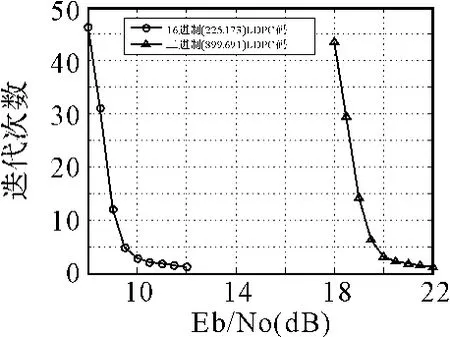
图4 16进制（225，173）LDPC码和二进制（899，691）LDPC码编码调制系统的平均迭代次数

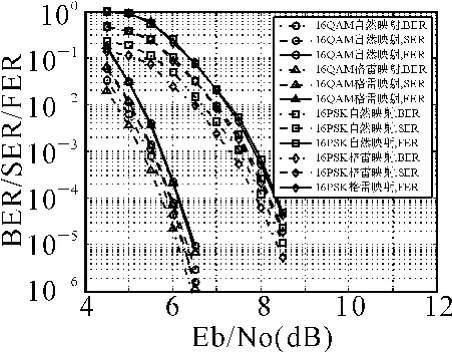
图5 16进制（120，60）QC LDPC码编码调制系统的误码性能

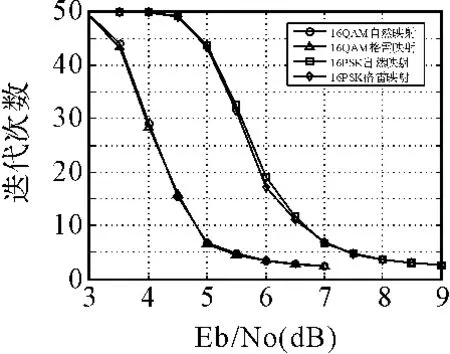
图6 16进制（120，60）QC LDPC码编码调制系统的平均迭代次数

5 结语

LDPC码的优异性能及其在信息可靠传输中的良好应用前景已引起世界各国学术界和IT业界的高度重视，成为当今信道编码领域最瞩目的研究热点。为保证编码调制系统的可靠性和有效性，提高数据的传输速率，本文建立了LDPC编码调制系统，给出了AWGN信道下二进制和多进制LDPC码迭代译码的初始化条件，研究了在LDPC码进制数与高阶调制阶数不匹配时软信息的转换方法，分析了二进制和多进制LDPC编码调制系统在AWGN信道下的性能。仿真结果表明，LDPC编码调制系统在AWGN信道下采用格雷映射方式优于自然映射方式，采用16QAM调制方式优于16PSK调制方式，多进制LDPC－BICM系统的性能优于二进制LDPC－BICM系统。

［1］Gallager R G.Low－Density Parity－Check Codes［M］.Cambridge，MA：M.I.T.Press，1963.

［2］Tanner R M.A recursive approach to low complexity codes［J］.IEEE Transactions on Information Theory，1981，27（6）：533－547.

［3］MacKay D J C.Good error－correcting codes based on very sparse matrices［J］.IEEE Transactions on Information Theory，1999，45（2）：399－431.

［4］Davey M C，MacKay D.Low－density parity check codes over GF（q）［J］.IEEE Communications Letters，1998，2（6）：165－167.

［5］张锦鹏，程明，王俊山.基于FPGA的18b20的CRC校验码的并行算法及实现［J］.计算机与数字工程，2011，39（4）.

［6］魏艳，马吉明.基于GPON的CRC算法分析及实现［J］.计算机与数字工程，2008，36（4）.

［7］陈俊斌.多进制LDPC码与RS码的性能比较研究［D］.厦门：厦门大学，2006.