编织参数对轴编C/C复合材料热膨胀系数的影响①

李书良，顾靖伟，李国才，史宏斌，侯 晓

(1.西北工业大学航天学院，西安 710072;2.中国航天科技集团公司四院四十一所，固体火箭发动机燃烧、结构与内流场国防科技重点实验室，西安 710025)

0 引言

轴编C/C复合材料是一种先进的抗烧蚀复合材料，因其力学和热物理特性能较好地符合固体火箭发动机的热结构要求而成为各国发动机喉衬的首选材料。C/C复合材料成型工艺复杂，生产成本高，众多学者希望通过对C/C复合材料的性能开展理论预报，从而在材料的研制初期就给出最佳的材料设计方案。多维编织C/C复合材料的热膨胀性能是固体发动机最为重要的指标，较低的热膨胀系数一直是材料研究的方向。为了研究编织结构对材料热膨胀系数的影响，已经有一些学者结合编织复合材料的结构特征，开展了热膨胀系数的预报和优化工作，这些工作主要涉及到预报方法和组分材料性能的确定两方面。针对前者，刘书田等［1］采用均匀化方法解决了复合材料的热膨胀问题。张卫红等［2］导出的基于能量法的复合材料热膨胀系数预报方法较均匀化方法更便于计算，在国内逐步得到推广。针对后者也开展了相应的工作，Sakai M［3］发现PAN炭纤维经过2 273 K温度石墨化后将由(230±5)GPa增加到(350±5)GPa。Soydan Ozcan［4］的实验表明，C/C复合材料热处理温度从2 073 K变化到2 673 K对纤维和基体的微结构和模量产生了较大的影响。Bacon等［5］测试了单向纤维增强C/C复合材料中纤维束内基体碳的原位弹性模量和热膨胀系数，结果表明基体的性质既依赖于基体的前躯体，也依赖于和基体复合的纤维。这些学者所开展的工作为进行C/C复合材料的热膨胀性能预报提供了参考。由于轴编C/C复合材料是国内新近研制成功的复合材料，当前尚未对其热膨胀性能进行系统研究。

本文基于轴编C/C复合材料的编织结构特征，采用能量预测法预报了该材料的线膨胀系数，通过对不同编织间距和纤维棒直径的材料模型的热膨胀系数进行预报，获得了该材料热膨胀系数和编织参数之间的关系。

1 基于能量法的复合材料热膨胀性能预报方法

能量法的基本思想:利用微结构和均质等效体的关系，通过推导复合材料等效性能与微结构变形能量的关系，得出复合材料等效性能的能量表达式。

对于复合材料微结构而言，当温升为ΔT时，微结构的平均应力与平均应变存在以下关系:

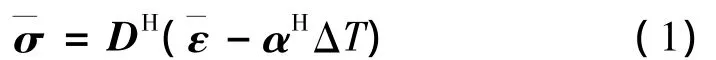
定义微结构的变形能为

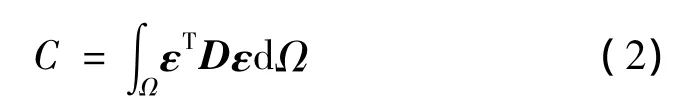
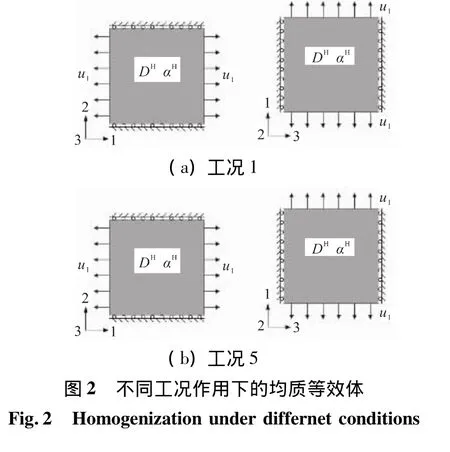
不同工况作用下的微结构、均值等效体如图1、图2所示。对于图1(a)所示的工况1(u2=u3=0)，ΔT温度变化，微结构的平均应力、应变条件为=0=0，上标(1)代表工况。将其代入式(1)求解可得微结构的1方向平均应变与2、3方向的平均应力:

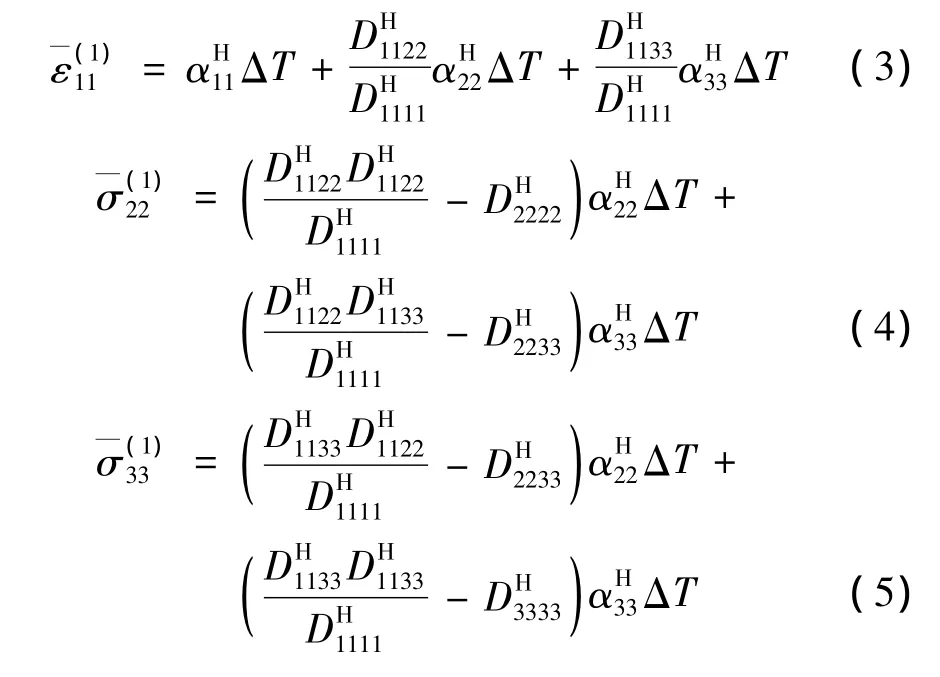
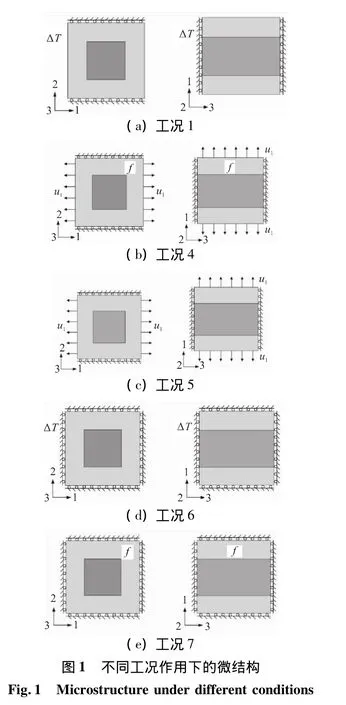
工况1作用下的微结构可等效为无温度载荷作用的微结构工况4(图1(b))，图中的位移载荷u1与工况1作用下的位移载荷相等，力f为2种载荷间热应力的不同而引起的界面力，二者的表达式为

同理，工况1作用下的均质等效体(图2(a))可等效为工况5无温度载荷作用下的均质等效体(图2(b))，二者的变形能相等，即

根据相同周期性边界条件下(无温度载荷)均质等效体的变形能与微结构的变形能相同这一原则可知，工况5作用下均质等效体的变形能与微结构的变形能(图1(c))相同，即

现在对微结构施加图1(d)所示的边界条件(工况6)，其等效无温度载荷的边界条件为图1(e)所示的工况7。同理，2种工况下微结构的变形能相等:

工况1作用下微结构与均质等效体的变形能的关系可转成工况4与工况5作用下微结构变形能的关系。

工况4、工况5和工况7分别作用下的微结构有限元方程可表示为

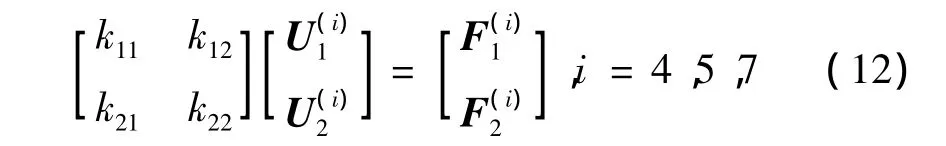
求解方程(12)可得

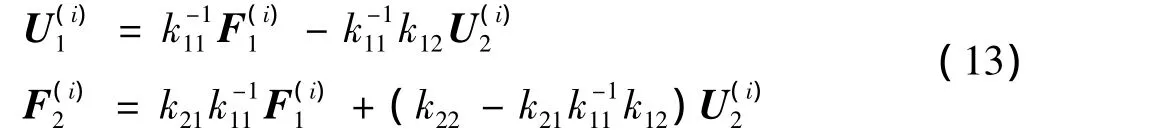
结合式(2)变形能定义式可得微结构变形能的通用表达式为

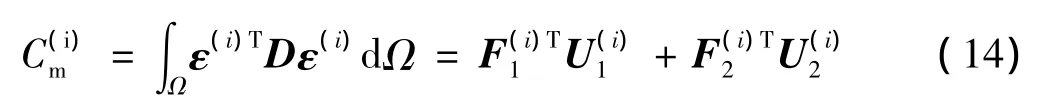
可以证明工况4、5、7作用下微结构的变形能存在如下关系:

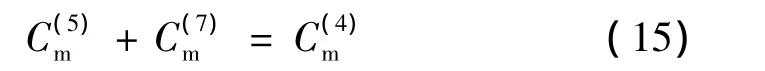
结合式(9)、式(10)、式(11)可得到在工况1作用下微结构的变形能与均质等效体变形能的关系:

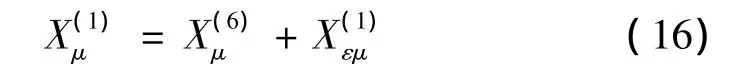
工况1作用下均质等效体的变形能为

同理，对于工况2(u1=u3=0)和工况3(u1=u2=0)，可得

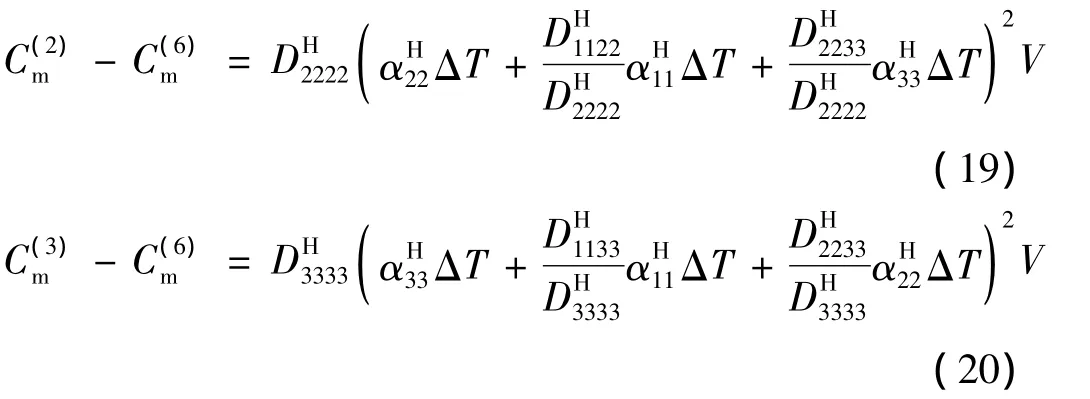
式(18)～(20)描述了微结构变形能与其等效热膨胀系数的关系，求解以上各式可得微结构等效热膨胀系数的变形能计算式:

其中:

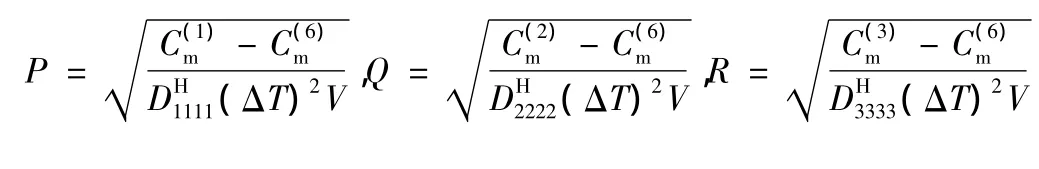
2 轴编C/C复合材料物理力学性能预报

2.1 有限元模型

轴编织C/C复合材料从宏观的角度来看，是由纤维棒、纤维束、煤沥青基体和界面组成，其代表性体积单元(RVE)如图3所示。

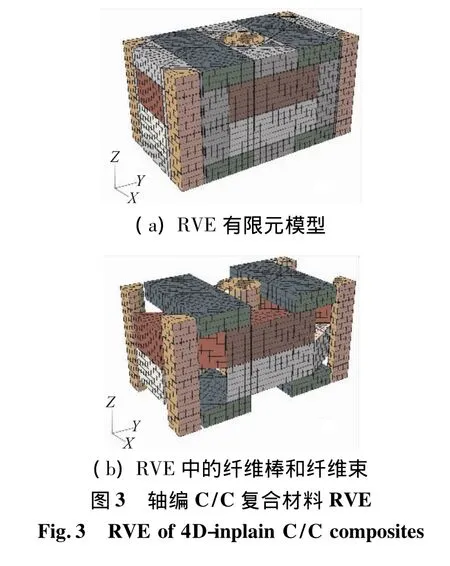
网格的划分和后续周期性边界条件的施加有关，因此需要严格保证单胞对应面网格节点一致。本文采用C3D8和C3D6单元对代表单元进行离散。

2.2 组分相性能

组分相的力学性能参照文献［6］。其热膨胀性能分别采用第2节的能量求解法及式(22)和式(23)的解析表达式［7］求出。

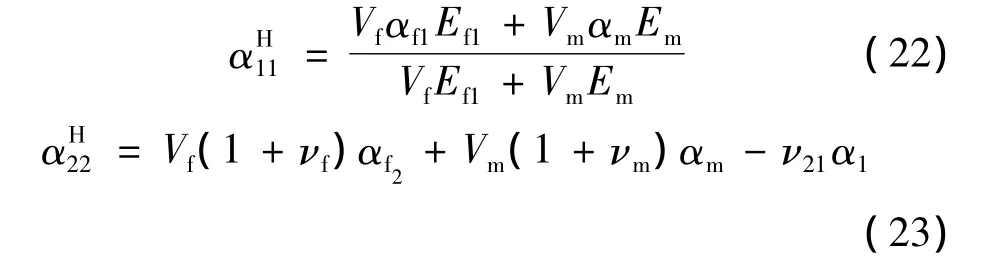
根据 Bacon［5］和 Jae－Seok［8］的工作，T300 纤维和基体的热膨胀系数取值见表1。

表1 纤维和基体的热膨胀系数Table 1 CTE of fibers and matrix

轴编C/C复合材料中纤维棒和纤维束的纤维体积分数分别为68%和62%。以表1数据为输入参数，采用解析法和能量法求得的纤维棒和纤维束热膨胀系数见表2。2种方法计算结果具有较高的一致性，最大误差不大于6.5%，显示了能量法求解热膨胀系数的有效性。

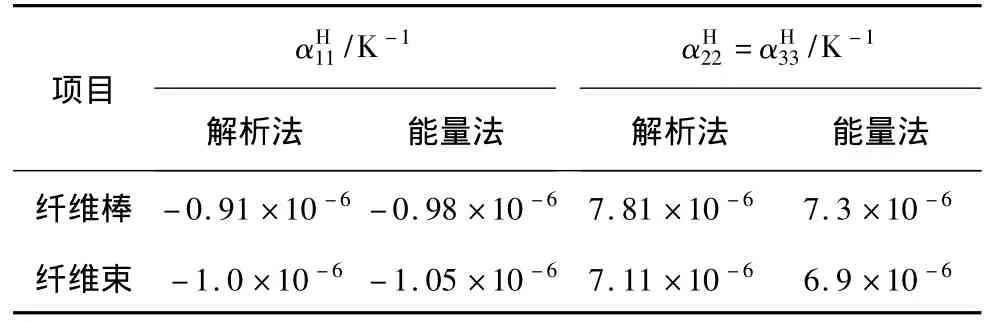
表2 增强相的热膨胀系数Table 2 CTE of enhance phase

2.3 轴编C/C复合材料热膨胀性能分析

基于表1和表2所列组分材料参数，采用能量分析法对图3所示的单胞模型的热膨胀性能进行预报，其预报结果和实验结果的比较见表3。表3中的热膨胀实验数据采用DIL 402热膨胀仪进行测试，试样尺寸为φ6 mm×50 mm。

对比表明，基于能量法的热膨胀系数预报方法具有一定的预示精度，轴向和径向的误差分别为8%和3.4%。预测值均比实验值高，这可能是由于基体的热膨胀系数取值大于真实值所致。

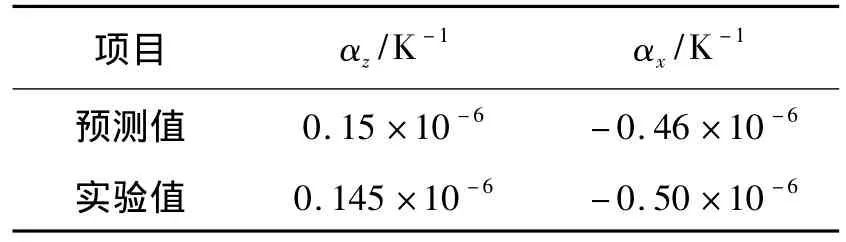
表3 轴编C/C复合材料常温热膨胀系数Table 3 CTE of 4D in-plane C/C composites at room temperature

为更客观描述编织间距和纤维棒直径对材料热膨胀性能的影响，定义当前的纤维棒中心间距和纤维棒直径为L0和D0，Li和Di为目标间距与当前间距和目标直径与当前直径的比值，通过改变这个比值实现纤维棒中心间距和直径的改变，从而研究二者对热膨胀性能的影响。

所获编织间距对热胀系数的影响如图4所示。随着编织间距的增加，轴向和径向的热膨胀系数逐渐降低。其主要原因在于编织间距增大，在RVE内轴向纤维棒和径向纤维束的体积含量均降低，而基体的体积分数增加;由于基体热膨胀系数较纤维棒和纤维束都低，当其体积分数增加，而纤维棒和纤维束体积分数降低后，必然引起热膨胀系数的整体下降。

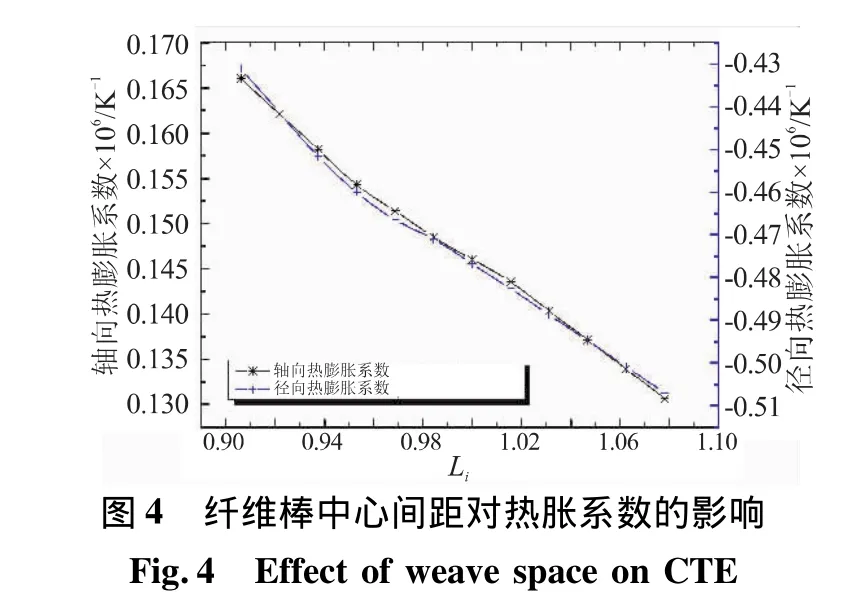
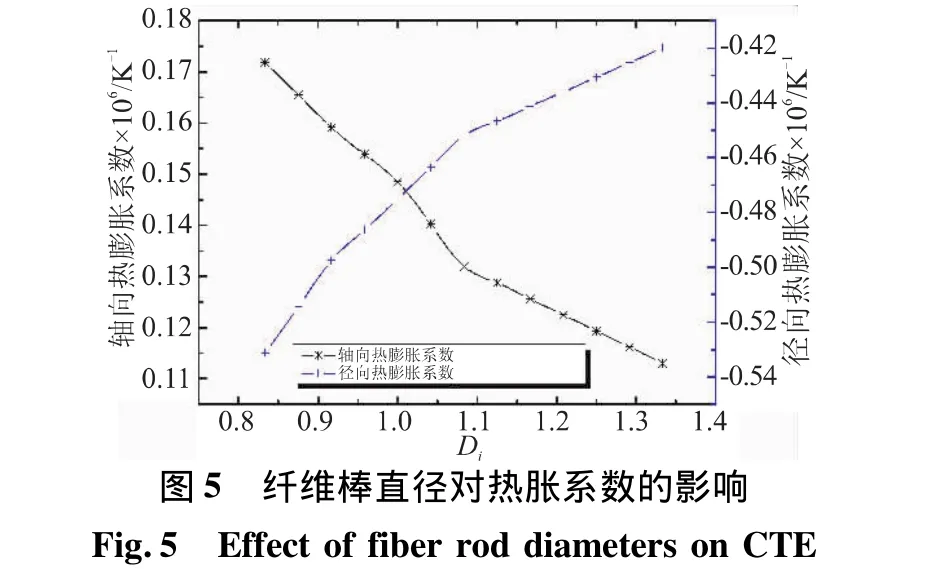
图5表现了纤维棒直径对热胀系数的影响，随着纤维棒直径的增加，轴向热膨胀系数显著降低。这主要是因为在编织间距不变的情况下，纤维棒直径增大，显著增加了单胞中轴向纤维的含量，又由于轴向纤维的热膨胀系数较低，从而导致材料轴向热膨胀系数的降低。

径向热膨胀系数是纤维棒直径的增函数，但增量较小。其原因在于基体的热膨胀系数较纤维棒的横向热膨胀系数小，当纤维棒体积分数增加，基体的体积分数减小时，纤维棒横向热膨胀系数对材料径向热膨胀系数的贡献大于基体对径向热膨胀系数的削弱所致。

3 结论

(1)基于能量法的热膨胀系数预报方法在预报纤维棒和纤维束的热膨胀系数时与解析法吻合较好，显示了能量预报法的有效性。

(2)采用能量法预报轴编C/C复合材料的热膨胀性能时与实验值吻合较好，具有较高的精度，可作为编织C/C复合材料性能预报的有效方法。

(3)轴编C/C复合材料的常温热膨胀系数随编织间距的增大而减小;随半径增大，轴向热膨胀系数逐渐减小，而径向热膨胀系数逐渐增加。

［1］刘书田，程耿东.基于均匀化理论的复合材料热膨胀系数预测方法［J］.大连理工大学学报，1995，35(5):451－457.

［2］Zhang W H，Wang F W，Dai G M，et al.Topology optimal design of material microstructures using strain energy－based method［J］.Acta Aeronautica Astronautica Sinica，2007，20(4):320－326.

［3］Sakai M，Matsuyama R.The pull－out and failure of a fiber bundle in carbon fibers.Carbon，2000，38:2123－2131.

［4］Soydan O，Peter F.Microstructure and wear mechanisms in C/C composites［J］.Wear，2005，259:642－650.

［5］Bacon R.碳/碳复合材料中基体碳的性能［J］.新型碳材料，1990，19(1):39－41.

［6］唐敏，高波，杨月城，等.基于均匀化方法的轴编炭/炭复合材料性能预测［J］.固体火箭技术，2011，34(1):109－112.

［7］沈观林，胡更开.复合材料力学［M］.北京:清华大学出版社，2006.

［8］Jae－Seok Yoo.Thermoelastic analysis of kick motor nozzle incorporating spatially reinforced composites［J］.Journal of Spacecraft and Rockets，2003，40(1):83－91.