轴编C/C复合材料组分材料有效性能①

方国东，韩杰才，梁 军，孟松鹤，杨 宇

(1.哈尔滨工业大学 特种环境复合材料技术国防科技重点试验室，哈尔滨 150080;2.哈尔滨工业大学 材料科学与工程博士后流动站，哈尔滨 150001)

0 引言

由于C/C复合材料在制备的过程中经历了炭化和石墨化等高温过程，所以其内部组分材料炭纤维和基体性能较固化时的性能都发生了很大的变化［1］。研究人员致力于利用组分相材料的性能表征复合材料的性能，建立组分材料的性能与最终复合材料性能的联系，并进一步实现复合材料的细观结构设计［2］。但目前由于组分材料原位性能的缺乏，严重阻碍了复合材料的设计和应用。

获得复合材料组分材料有效性能的方法有很多，Steen和Valles［3］从改进的剪滞模型得到启发，利用拉伸试验标定5个参量，确定纤维和基体弹性模量、界面摩擦系数和界面法向粘接强度。程添乐和夏源明［4］利用混合率和Evans等导出的加载后卸载-再加载应力-应变曲线迟滞回环和组分材料力学性能之间的关系，反推出纤维的原位模量。Ojard等［5－6］通过纤维束测试或纳米压痕的方法，确定陶瓷基复合材料内部纤维束的弹性模量，但组分相还很难从复合材料中剥离出来，且依赖于设备测量精确度等因素。Song等［7－8］对编织复合材料进行横向单轴压缩实验，结合编织复合材料的有限元计算模型，反推原位基体性能。该方法要求编织复合材料横向压缩试验主要是基体剪切破坏，但纤维束的影响还是很难剔除，这种试探性反推方法只能针对这种特定织构的编织复合材料。由于编织复合材料内部基体中纤维的存在，即使纯基体与复合材料形成的工艺过程相同，编织复合材料内部基体性能还是与纯基体有很大区别，所以不能通过测试同种工艺得到的块状材料来确定复合材料内部组分材料的原位性能。目前，对编织复合材料的宏观有效性能测试还是相对较成熟，且测量的可靠性较高，所以利用宏观有效性能反推细观组分材料性能，但不能试探性地去反推，也不能局限于一种织构的编织复合材料。人工神经网络方法具有强大的非线性、并行分布结构和学习归纳能力等特征，并能把低维空间线性不可分的问题在高维空间线性可分［9］。所以，也使这种从编织复合材料宏观有效性能反推细观组分材料原位性能(多种影响因素)成为可能。但人工神经网络是否有很好的预报能力，取决于构造的样本质量、选择的网络类型、激励函数及学习方式等因素。

本文利用径向基函数神经网络方法，反推组分材料的有效性能，给定编织复合材料内部组分材料有效性能参数的取值区间，随机给定内部组分材料有效性能的不同组合形式，利用编织复合材料代表体积元方法结合有限元方法，构造神经网络的输入输出向量，经过神经网络训练得到鲁棒性较强的网络，最后通过输入轴编C/C复合材料宏观力学性能试验测得有效性能参数，预报编织复合材料内部组分材料的有效性能。

1 轴编C/C复合材料有效性能预报

1.1 几何模型及有限元模型

本文研究的轴编C/C编织复合材料，采用拉挤成型的细炭纤维刚性棒混编的4D预制体，其预制体的编织结构如图1所示。经沥青浸渍、炭化、致密化工艺及高温处理的高压沥青浸渍炭化致密化工艺(HIPIC)，制成高密度(1.93～1.94 g/cm3)4D C/C喉衬材料［10］。

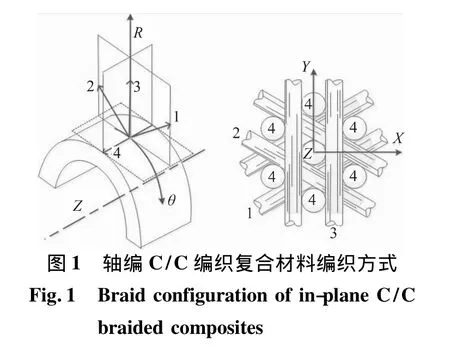
通过对轴编C/C编织复合材料垂直于刚性炭棒和一个面内纤维束方向进行切割，利用光学显微镜观测轴编C/C复合材料的几何结构特征，测量编织结构细观结构参数，建立相应的材料周期性几何单元模型。该轴编C/C复合材料分别由沿Z向的刚性炭棒、轴-环面内分别与轴成0°、60°和120°的炭纤维束(沿Z轴按顺序排布)和炭基体组成。Z向的炭棒为圆形，面内纤维束的横截面形状基本为长方形，内部由6股纤维束组成，如图2所示。

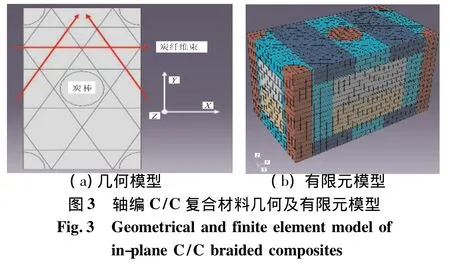
建立几何模型和有限元模型如图3所示。面内纤维束与纤维束之间有一层很薄的炭基体层，炭棒与炭纤维束之间也有一层薄的炭基体。同时，把0°的炭纤维束方向定义为X方向，60°和120°炭纤维束方向对应Y向，炭棒方向为Z向。

1.2 编织复合材料有效性能计算

假设轴编C/C复合材料的宏观应力-应变关系可表示为

式中 {σM}和{εM}分别为复合材料的宏观应力和应变;{αM}为复合材料的热膨胀系数;{CM}为复合材料的刚度矩阵;ΔT为温差。

本文采用边界位移法，对代表体积单元施加位移边界条件，没有温差变化。所以，材料的应力应变关系可写为

要得到刚度矩阵，需分别在1、2、3法向方向和12、13和23切线方向加载。经过6次加载计算，分别计算代表单元的应力响应，经过对应力的体积平均可得到代表体积单元的宏观平均应力{σM}，从而分别求得刚度矩阵的每一列。

在计算过程中，为了保持代表体积单元的周期性，必须对代表体积单元施加周期边界条件，要求代表体积单元平行面上的对应点具有大小相等、方向相反的力，且对应点的位移协调一致，即对应点位移和力连续，从而保证代表体积单元变形的周期性(如图4所示)。在文献［11］中证明了当代表体积单元满足位移的连续性，力也相应满足连续条件。

例如，利用边界位移法求取刚度矩阵的第1列，需在x方向施加非零位移，要求对应面(如面A1D1D2A2和面B1C1C2B2)对应节点施加位移耦合约束(如点A3和 B3，D3和 C3之间)，即

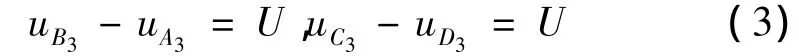
其中，U为施加的位移量。但这样施加非零位移，要求代表体积单元对应平面上的节点也是相对应的。然后，其他相对应面上相对应的节点施加零位移耦合约束。从而x方向的宏观应变不为零，其他宏观应变分量为零。经过有限元计算，代表体积单元出现相应的应力响应，经过对代表体积单元体积平均计算宏观应力分量，即

式中 Vj为单元体积;为j单元i方向的应力分量;ne为代表体积单胞的单元总数。

通过式(2)就可求出宏观刚度矩阵的第1列。然后，通过施加不通过的边界条件，经过6次分析，确定整个刚度矩阵，对刚度矩阵求逆得，到相应的宏观柔度矩阵［SM］，再利用式(5)得到轴编C/C复合材料的工程材料常数。

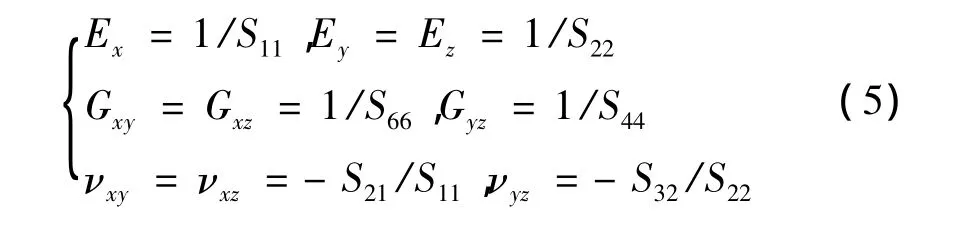
2 构造神经网络

2.1 构造神经网络的输入输出向量

如果组分材料的力学性能及轴编C/C复合材料的细观编织结构已知，则通过有限元计算，可得到轴编C/C复合材料的有效性能。本文轴编C/C复合材料采用T300炭纤维，则炭纤维的性能如表1所示。假设编织复合材料内部纤维束的性能表现为横观各向同性，基体是各向同性的，具有2个独立的弹性常数(Em、νm)。利用细观力学模型，得到纤维束的有效性能［12］，如表1 所示。

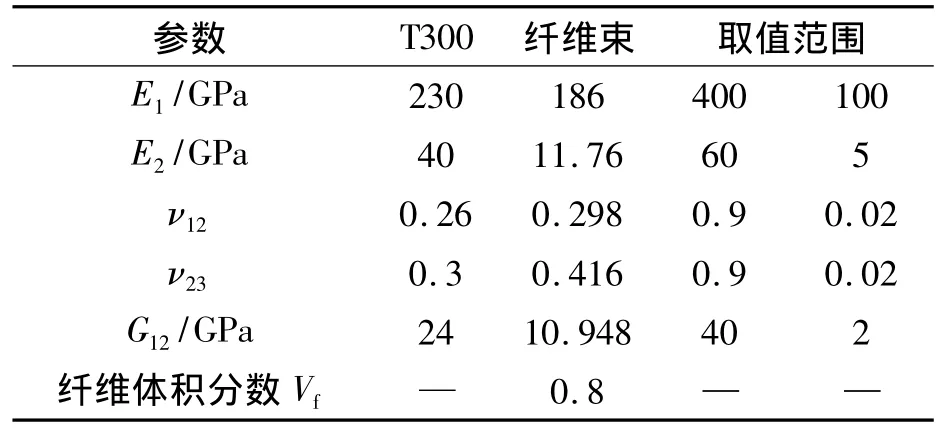
表1 组分材料的材料性能及变化范围Table 1 Mechanical properties and variation range of constituent materials

表1中给出的纤维有效性能是原丝的有效性能，经C/C复合材料成型工艺后，炭纤维的原位性能与原丝性能相比发生很大变化。通过炭纤维原丝的性能，确定纤维束的性能，可通过实验估计给定最大值和最小值，确定纤维束变化的范围，使原位纤维束的有效性能落在范围之内。

根据材料的弹性常数的热力学限制，刚度矩阵和柔度矩阵是正定的，即要求刚度矩阵及柔度矩阵对角线元素必须是正的，进一步要求:

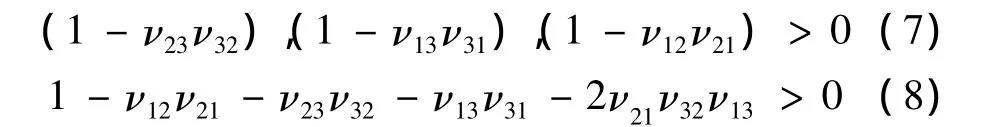
通过表1给出的组分材料有效性能及其变化范围，把每个单一有效性能分为A个值，通过不同组合(每个组合可认为是一个向量)构造不同的虚拟实验。如果把所有的组合都考虑，那就会出现AN个组合(也可认为构成一个由AN个向量构成的曲面)，其中N是组分材料有效性能的个数。为了尽量包含有代表性的虚拟实验组合(也就是找有代表性的向量把整个曲面的主要特征都体现出来)，采用随机选取组分材料性能进行虚拟实验，构造组分材料有效性能与编织复合材料有效性能的对应关系。于是得到的编织复合材料有效性能作为神经网络的输入向量，组分材料有效性能作为神经网络的输出向量。

2.2 径向基函数神经网络

式中 ε为近似过程中的误差;wi为权函数;Gi(x)为高斯函数;NRBF为径向基函数的个数。

Guass函数为单向径向变化函数，可表示为

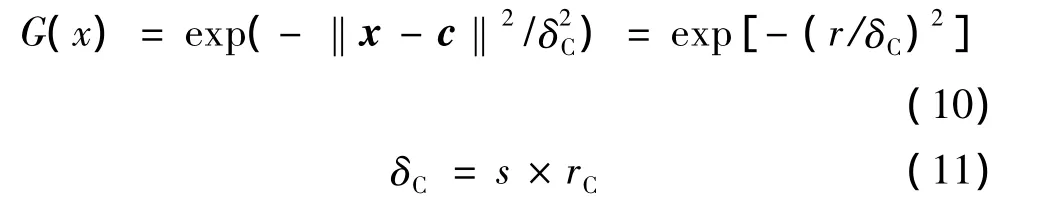
式中 ‖·‖为矢量范数算子;c为径向基函数中心;rC为径向基函数的半径;s为宽度参数。

径向基函数网络学习要求解这3个参数:径向基函数的中心、宽度和隐含层到输出层的权值。本文通过自组织选取中心法来确定径向基函数中心，利用伪逆法确定径向基函数网络的权值［13］。

该网络运行的步骤如图5所示，为了降低网络对输入样本的依赖，利用随机选取符合平均分布的炭纤维束力学性能构造输入样本，多次循环训练网络，预报编织复合材料的组分材料有效性能，经过多次循环后，通过误差函数确定与目标误差较小的结果，选取的误差函数为

式中 Ne为编织复合材料有效性能数。

3 结果及分析

3.1 轴编C/C复合材料有效性能预报

对轴编C/C复合材料面内的有效性能进行预测，图6 为面内性能 E1、E2、G12、G23和 G13随面内旋转角度的变化关系。

从图6中可看出，面内弹性性能和剪切性能随面内角度的变化都非常小，可认为E1与E2、G13与G23相等，可假设 E1、E2、G12、G23和 G13在面内的性能不随角度不同而变化。所以，该轴编C/C复合材料宏观有效性能的独立参数为6个。在对轴编C/C复合材料进行宏观实验时，面内纤维束的铺设方向也很难把握，通过预报面内有效性能，发现测量面内E1或E2性能时，可不必考虑面内纤维束铺设方向的影响，这方便了实际轴编四向C/C复合材料的面内有效性能测试。

3.2 神经网络性能测试

为了说明神经网络与训练样本的关联性，通过随机选取符合平均分布的组分材料参数构造训练样本，利用160个样本对网络进行训练。然后，利用网络对给定宏观有效性能的编织复合材料组分材料性能进行预报，如果预报的组分材料性能出现负值，舍弃该网络，重新生成训练样本，对网络重新训练，最后得到满足基本条件的预报结果。图7是循环次数N为100时，有89个有效的网络，图7给出了预报的组分有效性能对应的宏观编织复合材料的有效性能，通过误差函数可判断最理想的预测结果是第67次，同时也可看出，训练样本的选取对网络的性能产生很大的影响。

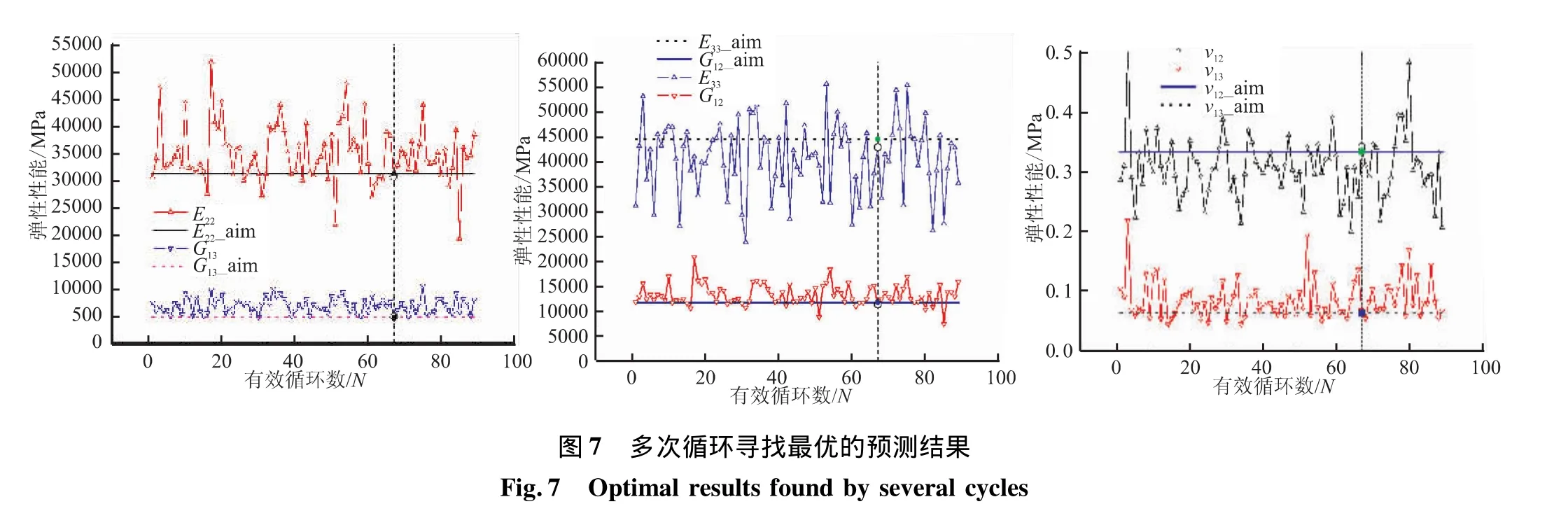
表2是寻找最理想的组分材料性能预测值。其中，Ec1、Ec2、νc12、νc13和 Gc12是面内纤维束的有效性能;Ef1、Ef2、νf12、νf13和 Gf12是轴向炭棒的有效性能;Em、νm是基体的有效性能。

表2 测试网络预测与目标的结果比较Table 2 Comparison of predictive and aim results

从表2中可看出，神经网络对编织复合材料组分材料的弹性模量和剪切模量可进行很好地预测，但对组分材料泊松比的预测结果较差。这主要是由于组分材料泊松比对编织复合材料宏观性能影响不明显，从而组分材料泊松比与宏观材料性能的关联性较差。通过多次循环训练网络，对编织复合材料组分材料性能进行预报，结合误差函数可得到最接近目标的预测结果。

3.3 组分材料原位性能预报

文献［10］对轴编C/C复合材料的有效性能进行了测试，如表3所示。由于测试结果较单一，也没有给出相应的误差范围。由于拉伸模量一般测量较为准确，所以在本文中，对预报的组分材料性能对应的轴编C/C复合材料的拉伸模量进行了误差评测，最终得到了接近该复合拉伸弹性模量的预报结果，如表4所示。从表4中可看出，剪切模量和泊松比与目标值相差较大，通过多次选取训练样本也很难与文献［10］中给出的实验结果相符，这也说明了神经网络有很大的容错性。

表5给出了通过神经网络预报得到的轴编C/C复合材料组分材料的性能。如果给出多个实验结果值，可预报得出相应组分材料的原位性能，如果组分材料性能预报结果对应宏观性能与实验结果相差较大，也说明实验结果存在一定偏差，还需进行大量宏观实验。本文通过神经网络方法能够对轴编C/C复合材料组分材料的原位性能进行很好地预报。

表3 轴编C/C复合材料各向刚度性能［10］Table 3 Stiffness properties of 4D in-plane C/C composites［10］

表4 预测的结果对应宏观材料性能与实验结果对比Table 4 Comparison of predicted and experimental results of macroscopic effective behavior of braided composites GPa

表5 组分材料有效性能预测结果Table 5 Predicted results of effective properties of constituent materials GPa

4 结论

(1)通过预报轴编C/C复合材料面内有效性能，发现弹性性能和剪切性能随面内角度的变化都非常小。所以，在测量面内有效性能时，可不必考虑面内纤维束铺设方向的影响。

(2)人工神经网络性能与训练样本相关，通过多次循环训练网络，对编织复合材料组分材料性能进行预报，从而可得到最接近目标的预测结果。

(3)由于编织复合材料宏观性能表现一定的离散性，细观组分材料性能也相应地出现一定的离散型。所以，该方法的可靠性主要依赖于编织复合材料宏观有效性能的实验测定。通过该方法得到组分材料有效性能后，可进一步进行数值计算，改变编织结构，设计出工程需要的编织复合材料。

［1］John D B，Dan D E.Carbon-carbon materials and composites［M］.Noyes publications，Park Ridge，New Jersey，USA，1993.

［2］Li D S，Lu Z X，Chen L，et al.Microstructure and mechanical properties of three-dimensional five-directional braided composites［J］.Inte.J.Solids Stru.，2009，46:3422-3432.

［3］Steen M，Valles J L.Determination of in-situ fibre，matrix and interface properties in a composite using tensile tests and an extended shear-lag model［J］.Mater.Sci.Engrg.，1998，A250:217-221.

［4］程添乐，夏源明.一种测定单向纤维增强陶瓷基复合材料组分“原位”弹性模量的方法［J］.复合材料学报，2007，24(1):75-80.

［5］Gowayed Y，Ojard G，Miller R，et al.Correlation of elastic properties of melt infiltrated SiC/SiC composites to in situ properties of constituent phases［J］.Compos.Sci.Technol.，2010，70:435-441.

［6］Ojard G，Rugg K，Riester L，et al.Constituent properties determination and model verification for a ceramic matrix composite systems［J］.Ceram.Eng.Sci.Proc.，2005，26(2):343-50.

［7］Song S，Waas A M，Shahwan K W，et al.Braided textile composites under compressive loads:modeling the response，strength and degradation［J］.Compos.Sci.Technol.，2007，67(15-16):3059-3070.

［8］Song S J，Waas A M，Shahwan K W，et al.Compression response of 2D braided composites:single cell and multiple cell micromechanics based strength preditions［J］.J.Compos.Mater.，2008，42(23):2461-2482.

［9］Anjum M F，Imran T，Khaled A S.Response surface methodology:a neural network approach［J］.European J.Operational Res.，1997，101:65-73.

［10］高波，唐敏，杨月城，等.4D轴编C/C复合材料力学性能实验研究［J］.复合材料学报.2011，28(6):245-250.

［11］Xia Z，Zhou C，Yong Q，et al.On selection of repeated unit cell model and application of unified periodic boundary conditions in micro-mechanical analysis of composites［J］.Inte.J.Solids Stru.，2006，43:266-278.

［12］Gommers B，Verpoest I，Van Houtte P.Modeling the elastic properties of knitted-fabric-reinforced composites［J］.Compos.Sci.Technol.，1996，56:685-694.

［13］傅荟璇，赵红，等.Matlab神经网络应用设计［M］.北京:机械工业出版社，2010.