分层次教学的模糊聚类分组模型

王 彦，马 丹，张国辉

(大庆师范学院 数学科学学院，黑龙江 大庆163712)

1 问题提出

所谓分层次教学是指在学生个体素质差异较大前提下，采用分组教学，不同组别采用不同教学方法或教学手段的一种教学模式。分层次教学需要精心组织，抓住不同组别采用不同教学方法或教学手段这个关键环节，周密实施，可以提高教学质量。

通常的组织方法都是采用单科成绩或总成绩排队来分组编班，然而这样的分组编班，由于同学们心理素质的不同导致考试时发挥的不同，不能客观地将个体素质差异不大的同学分到同一组，使得仍然个体差异较大的学生被分到同一组，导致不便于教学。为此，我们认为有必要对分层次教学的分组编班进行研究。通过对影响因素进行分析，我们认为学生的个体素质有些是通过各科成绩来表现的，而并非各科成绩能表现全部素质，换句话说，素质是蕴涵在学生各科成绩之中，素质难以定量评价。

2 分层次教学的模糊聚类分组模型的构建

分类是人们认识世界的基础。难以定量分析的事情，人们大都采用分类的方法来了解与认识。在社会、经济及自然现象的研究中，存在着大量分类研究的问题。我们时常要把所接触到的事物(样本)，按其性质、用途等进行分类，这种分类过程我们称为聚类分析。聚类分析的基本思想是根据对象间的相似程度进行类别的聚合。在进行聚类分析之前，类别是隐蔽的。通过聚类分析所产生的类具有同一类中的个体之间有较大的相似性，不同类中的个体之间差异性很大的特点。

聚类涉及事物之间的模糊界限时，需运用模糊聚类分析[1]。 模糊聚类分析广泛应用在气象预报、地质、农业、林业等方面。 通常把被聚类的事物称为样本，将被聚类的一组事物称为样本集。模糊聚类分析有两种基本方法：系统聚类法和逐步聚类法。系统聚类法是基于模糊等价关系的模糊聚类分析法。

学生个体素质难以定量分析，素质高低界限模糊，我们试图用模糊聚类分析方法进行分类。把需要分组编班的学生看作为待分类的一个集合U={u1,u2,…ui,…un},假设其中每个元素ui(i=1,2,…n)，即待分班的学生，有m项入学时各科成绩ui1,ui2,…uim(i=1,2,…n)，则可以用m维向量描述待分类的元素，即ui=(ui1,ui2,…uim),i=1,2,…n，相应的模糊聚类分组，按下列步骤进行：

(1)数据标准化处理。即对待分组编班学生集合U中的每个学生ui的各科分数数据ui1,ui2,…uim标准化处理：若uik是百分数，记u`ik=100-1uik，则u`ik∈[0,1]i=1,2,…n;k=1,2,…m。

(2)建立模糊相似矩阵[2]R=(rij)n×n其中

适当选取实数c，使得0≤rij≤1。

(3)依据所求得的模糊相似矩阵R=(rij)n×n和模糊矩阵的运算理论，求模糊等价矩阵[3]Rλ。

(4)根据所求的模糊等价矩阵Rλ进行模糊聚类分析，适当选取λ值，对学生进行分组编班。

3 分层次教学的模糊聚类分组模型的应用举例

为了叙述方便起见，我们取2010级10名学生的四门入学成绩为例，对模型的使用加以说明：

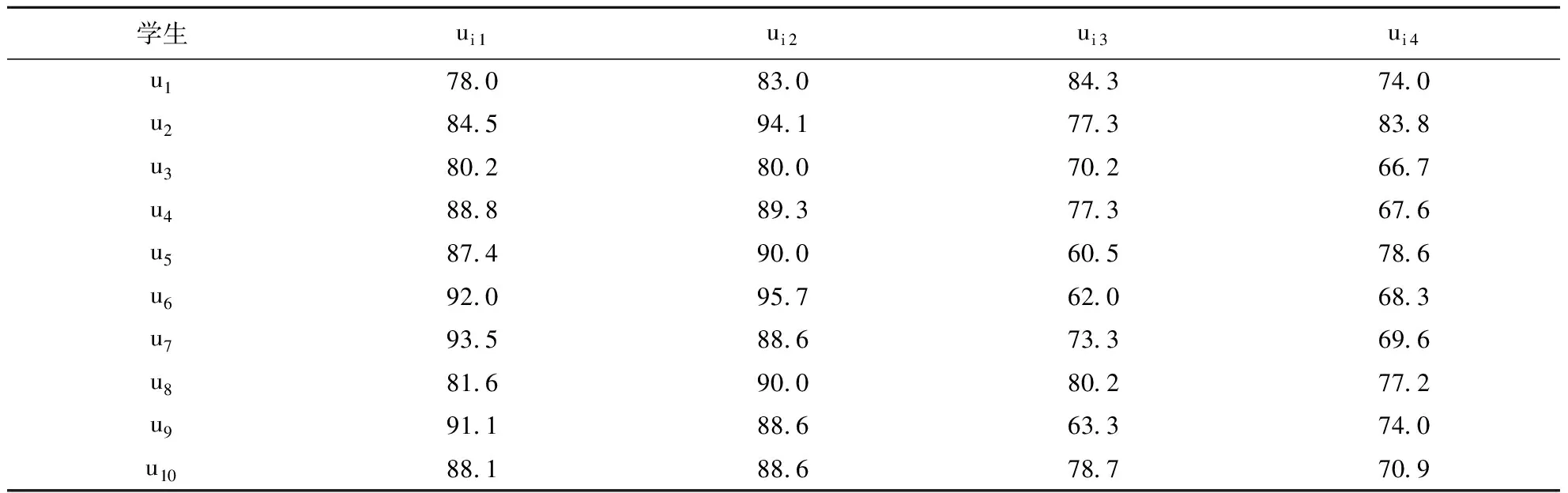
表1 学生的入学成绩

对上述取定的10同学的成绩进行标准化处理：

表2 学生的入学成绩标准化处理

取c=0.8，按绝对值减数法进行计算，得到模糊相似矩阵R：

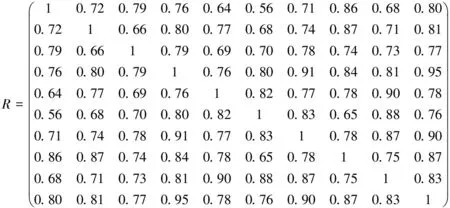
经过计算得到传递矩阵[4]R*：

在R*中取λ=0.87，得到相应的λ截矩阵R0.87：

对应的元素为：u1，u2，u3，u4，u5，u6，u7，u8，u9，u10。当λ=0.87时，将U分成三类：{u1}、{u3}、{u2,u4,u5,u6,u7,u8,u9,u10}。

4 分层次教学的模糊聚类分组模型的应用

我们对数学与应用数学专业2010级173名新生，依据入学的各科成绩，应用了上述模糊聚类分组模型进行分组编班，共分了四个教学班，其中一班44名学生，二班42名学生，三班41名学生，四班46名学生。 一班和二班合班上课，三班和四班合班上课，根据授课班学生的具体情况采用适当的教学策略和教学方法，经过三个学期的教学，各科教学的教师认为，由于这样的分组编班教学，每个教学班学生的基本素质差异较小，认知理解能力的水平基本相当，课堂教学过程顺畅，教学任务容易完成，通过每个教学班期末考试成绩看出，优劣生的学习成绩相差的不悬殊。

5 分层次教学的模糊聚类分组模型的评价

通过实践，我们认为分层次教学的模糊聚类分组模型有如下的优点：

1)应用分层次教学的模糊聚类分组模型进行分组编班，比按单科成绩或总分进行分组编班更能符合学生的实际情况，素质差异较小，基础差别不大的学生分到一个教学班，方便教学,有利于提高教学水平。

2)分层次教学的模糊聚类分组模型不仅能用于新生编班，还可以用于平时对学生进行分类，比如每学期末利用本学期所开设的各门课程的成绩重新聚类，看学生类别变动情况，为教学质量分析提供依据。

[参考文献]

[1] 高新波.模糊聚类分析及其应用[M]. 西安：西安电子科技大学出版社, 2004.

[2] 罗承忠.模糊集引论[M].北京:北京师范大学出版社, 2005:105-111.

[3] 孙宇锋.基于MATLAB的模糊聚类分析及应用[J]. 韶关学院学报:自然科学版, 2006, 27(9):1-4.

[4] 苏金明,王永利.MATLAB 7.0实用指南[M]. 北京:电子工业出版社, 2004:66-68.