三角函数选择算子的遗传算法在梯级水库优化调度中的应用

杨 侃，郑 姣，郝永怀，周 冉，刘国帅

(河海大学水文水资源学院，南京 210098)

遗传算法(genetic algorithm，GA)产生于20世纪60年代末到70年代初，该法不依赖于问题的具体领域，有很强的鲁棒性[1]．近年来，随着数学与计算机技术的发展，GA被引入到水库优化调度领域．马光文等[2]将采用二进制编码的标准遗传算法(simple genetic algorithm，SGA)应用于水电站优化调度，实现了较有效地在整个解空间寻优，更有把握达到全局最优或准全局最优．王大刚等[3]提出了基于十进制编码的 SGA，避免了由于二进制编码串很长而造成的算法搜索效率低的缺陷．针对 SGA存在收敛性及个体适应度求解方面的困难，王少波等[4]在 SGA 的基础上采用随个体适应度大小和群体分散程度自动调整的交叉概率 Pc和变异概率 Pm，提出了一种自适应遗传算法(adaptive genetic algorithm，AGA)，并通过实例证明：与 SGA相比，AGA能够加快收敛速度提高算法全局稳定性．而对于水库优化调度中GA在选择过程中可能造成的早熟所做的改进，目前为止鲜见报道．选择算子直接关系到下一代种群的质量，对GA的整个过程有着至关重要的影响，通过改进选择算子，有利于避免算法过早收敛．

梯级水库优化调度模型建立上，传统研究在处理水库间复杂水力联系问题上，或未考虑或采用简化处理方式，所建模型只做流量时间上的推移计算，未考虑流量传播过程引起的坦化变形问题[5-6]．基于此，笔者深入研究了在 GA中如何处理梯级水库间复杂的水力联系．

1 自适应遗传算法及其选择原理

以决策变量编码作为运算对象，根据种群中个体适应度进行遗传操作，在进化过程中对各代群体中的个体进行优胜劣汰，以找寻目标函数的最优解[3]．AGA采用随个体适应度大小和群体分散程度自动调整的交叉和变异概率，提高算法的优化能力．

1.1 常用选择方法及存在的问题

GA中常用的个体选择方式主要有轮盘赌选择法、锦标赛选择法、排序选择法．其中轮盘赌选择法是最常用的，该法基于比例适应度选择，利用各个体适应度所占比例的大小决定其子孙保留的可能性，要求适应度大于零．对于水库优化调度问题，由于考虑流量约束和出力约束后，常常建立施以流量和出力惩罚的适应度函数，这样就很难保证适应度非负．锦标赛选择法虽然对适应度取正负无要求，但不同的联赛规模可能带来不同的效果，而联赛规模的选择目前仍没有理论依据，因此该法也存在其局限性．排序选择法通过设置个体被选中的概率来处理包含负适应值的情况，但是由于被选中的概率常常是常数值，不会随进化状态变化，因此也有其局限性[7]．因此怎样对遗传算法的选择算子做改进，使其能够克服适应度非负的要求，是值得深入研究的一项工作．

1.2 基于三角函数的选择算子

三角函数选择算子实际上是一种对适应值进行非线性变换的方法，将适应度函数转化为三角函数值pi映射到[0，1]．文献[7]提出如下4种选择算子．

正弦选择算子

余弦选择算子

正切选择算子

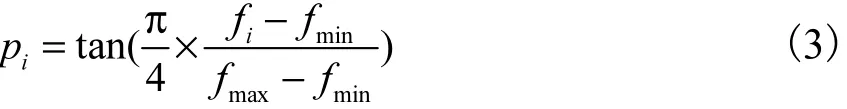
余切选择算子

文献[7]分析了三角函数选择算子的可行性，指出它能够保证适应值较优的个体具有较高的被选择概率．以正弦函数选择算子为例：对于同一种群内任意进化的 2个个体 xi和 xj，其适应度满足 fi＜fj，正弦函数显然，而正弦函数在[0，]上单调增，故．三角函数选择算子的概率是依据个体的适应能力设置的，能够很好地处理适应值为负值的情况．可以结合轮盘赌等进行传统选择算子的改进，因此很适合处理水库优化调度问题，具有很好的实用价值．

2 基于三角函数选择的梯级水库优化调度自适应遗传算法构建

梯级水库优化调度模型中每个水库每个时段都有最高最低水位约束，因此梯级水库调度的遗传算法在水库水位允许范围内，将单库调度期内水位前后连接，组成pop组可行水位变化序列，其中pop为种群数量．将水位进行一定的编码运算之后通过编码按照个体适应度进行“优胜劣汰”的进化过程．如此反复，最后按照一定的终止规则终止．对于水库优化调度问题，一般采用是否达到预定进化代数的方式终止运算．

2.1 初始种群设计及梯级水库间水力处理

初始种群的分布性质严重影响算法的收敛性能，初始群体性能差可能导致算法收敛速度慢，甚至不收敛[8-9]．考虑到库群编码是单库编码的数倍，采用随机生成初始种群的方式很难搜索到可行解，本研究采用文献[10]提出的解空间生成法．

梯级水库之间的水力联系使得其短期优化调度比单库优化调度复杂得多，传统研究处理水库间复杂水力联系问题时，或未考虑或采用简化处理方式．在下游水库入库流量的计算上，或简单地处理成上游水库出库流量和区间来水的总和，或只将上游水库出库流量做时间上的推移，实际上这样处理是非常不合理的，原因是上下游水库流量传播的过程中不仅存在时滞问题，还存在流量传播过程中带来的坦化变形．为此，笔者采用一种处理梯级水库间水力联系的新思路：以水库坝间实测的上游水库出库流量与下游水库相应入库流量资料来寻求其相关关系．这样可以很好地避免水流时滞和坦化变形处理，能够进一步提高模型的精度．

改进后模型中第i时段下游水库入库流量为

式中：d,iI为下游水库 i时段入库流量；u,iQ 为上游水库i时段出库流量；参数a、b由大量实测资料率定．

2.2 个体编码设计

避免二进制编码串很长造成搜索效率低的缺陷，采用实数编码．编码Kt，水位Zt，则

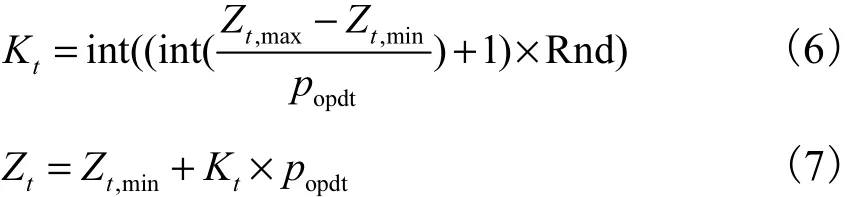
式中：tK为 t时段水位编码为t时段水位编码的上限；,maxtZ 、,mintZ 分别为t时段允许水位的最大和最小值；popdt为控制的水位精度．因为“以水定电”梯级水库调度模型中对每一水库都有初始和期末水位的限制，因此以第 1个水库为例(有初始水位 Z0和期末水位 Ze的控制)，对该水库初始和期末的水位编码为K0和Ke，即

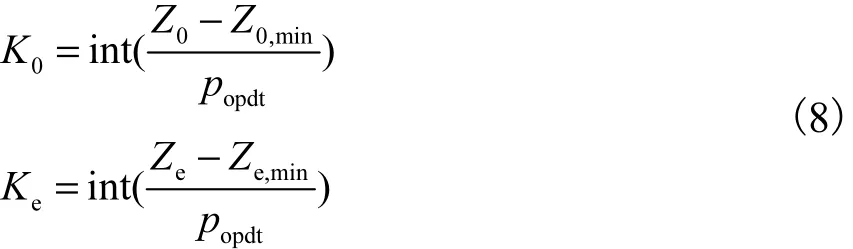
为避免因取整操作导致解码后 Z0、Ze的改变，遗传操作结束只按照式(7)进行中间时段的解码操作，而初始和期末水位按照Z0和Ze保持不变．

2.3 适应度函数设计

本研究为约束极大值优化问题，其中初始和期末水位约束、最高最低水位约束已经通过编码设计实现，对于其他约束，在下面适应度函数的设计中体现．单库的适应度函数为

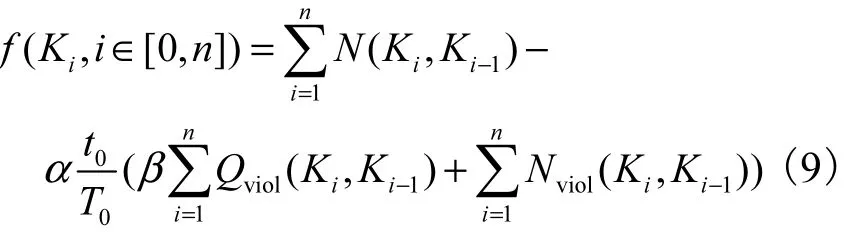
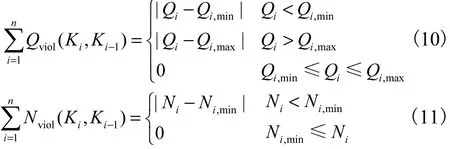
式中：Qi和 Ni为 i时段的下泄流量和出力；Qi,min和Qi,max为i时段允许下泄的最小和最大流量；Ni,min为i时段水库在电网要求下的最小出力．

对于出力的上限和下限，出力小于最小出力要求下的解为不可行解，已通过出力罚函数(式(11))进行惩罚处理．出力大于装机容量的解为可行解，大于装机容量则按照装机容量发电(即水电站机组处于满发状态)．

2.4 遗传操作设计

2.4.1 基于轮盘赌选择的正弦函数选择算子(正弦轮盘赌)设计

选择是建立在个体适应度计算基础上进行的．根据轮盘赌选择算子求解水库优化调度问题时无法克服适应度函数非负的情况，本研究将文献[8]提出的三角函数选择算子与轮盘赌选择算子结合使用，以正弦函数为例，建立正弦轮盘赌选择算子，以解决水库调度中适应度函数为负值的情况．其他 3种三角函数选择算子可类似使用．

以ip代替适应度函数if进行累积正弦函数值和累积正弦函数值比例的计算，在进行轮盘赌的选择过程中每一轮产生一个[0，1]的均匀随机数，对累积正弦函数值比例进行选择．适应度高的个体，正弦函数值大，在轮盘赌的选择中容易被保留，而适应度低的个体则易被淘汰．其中个体正弦函数值表示见式(1).

2.4.2 交叉和变异运算设计及参数自适应调整

采用以水库为单位进行的多点交叉和多点变异方式．考虑到设计的交叉算子需要有效地产生新个体以及水库调度中初始和期末水位编码固定的特殊性，采用文献[10]提出的有限制单点交叉方式．单库交叉断点在个体编码中的位置 s＝Rnd[1，n-2]；采用非均匀变异，以避免均匀变异不利于对某一重点区域进行局部搜索的问题．

式中：Ks和 Ks'为个体编码串中 s位变异前后的编码；B为系统参数，决定随机扰动对进化代数的依赖程度．

文献[4]已经证明了 AGA 优于 SGA，本研究采用文献[1]提出的参数的自适应调整公式．按照下列式子对交叉概率 Pc和变异概率 Pm进行自适应调整．另外为了保证每一代的优良个体不被破坏，在交叉和变异的过程中引入最优保存策略．

式中：c1P ＝0.9；c2P ＝0.6；m1P ＝0.1；m2P ＝0.001；fmax、favg、f′、f分别为群体中最大适应度值、平均适应度值、要交叉两个个体中较大适应度值和要变异个体适应度值．

3 三峡梯级实例分析

在处理三峡梯级水库间水力联系上，文献[11]提出常系数线性回归方程处理河段间水量传播的影响，并应用于三门峡小浪底水库联合优化调度．笔者在此基础上根据三峡梯级间河道水流传播特征，提出变系数流量传播回归方程，用以处理梯级流量传播中时滞与坦化变形 2个方面对优化调度的影响．考虑到三峡梯级两坝间河道特征，根据给定的实测相关资料对三峡水电站出库流量 Qsx与葛洲坝水电站相应入库流量 Qgzb进行率定．实测资料表明：当 Qsx＜16000m3/s时，Qgzb＜Qsx；当Qsx≥ 1 6000m3/s 时，Qgzb＞Qsx．因此，笔者探讨以Qsx＝16,000,m3/s为分界，以 Qsx为自变量，Qgzb为因变量，以观测点与配合的直线在纵轴方向的离差平方和最小(OLS)为准则，建立不同三峡出库流量下的线性回归方程，即

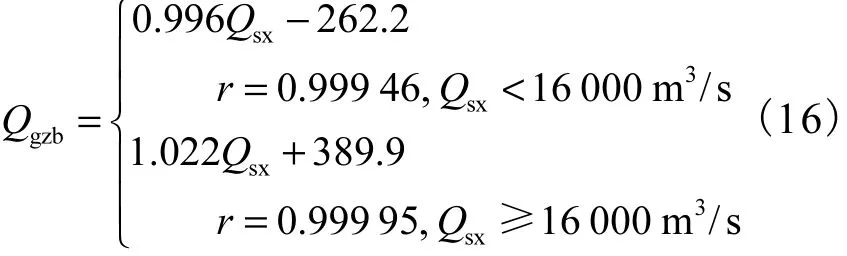
三峡梯级优化调度模型的目标函数为总出力最大，调度期T为1 d，划分为24个时段优化调度模型描述如下．

目标函数

式中：siN 和giN 分别为三峡和葛洲坝的阶段出力；N为总的出力和．

主要约束条件如下．

水量平衡约束

水位约束

下泄流量约束

出力约束

式中：Vi,j、Vi,j+1为 j时段 i水库初、末库容；Ii,j、QLi,j和 Q Si,j分别为j时段i水库入库流量、发电引用流量和弃水流量；Zi,min、Zi,t和 Zi,max分别为 i水库的死水位、t时段水位、正常蓄水位，假定“以水定电”模式中三峡水库初始和期末调度水位要求均为 175 m，葛洲坝水库均为66 m；Qi,min、Qi,t和 Qi,max分别为i水库的最小下泄流量、t时段下泄流量和时段最大下泄流量；Ni,min、Ni,t和 Ni,max分别为 i水库的保证出力、t时段出力和装机容量．在水量平衡约束中，三峡入库径流是已知的，葛洲坝的入库径流按照变系数线性回归方程(16)求得．

针对上述模型，分别采用本文提出的正弦轮盘赌选择算子和单纯轮盘赌选择算子进行 AGA求解，对三峡水库入库流量为中洪水时，以小时为计算单位进行调度模拟．计算中取种群数 pop为 100，水位精度popdt取 0.01 m．为了更好地比较二者的性能，分别以进化 10代、50代、100代、150代、200代、250代和300代作为终止条件进行模拟．考虑到GA是一种以随机理论模仿生物进化的搜索方法，本研究对2种方法每个进化代数下分别进行 10次演算，取其平均值对比如图1所示．由图1可以看出，改进后的选择算子在进化代数相同的情况下体现了较高的性能，说明改进后的选择算子使AGA能以较快速度收敛．

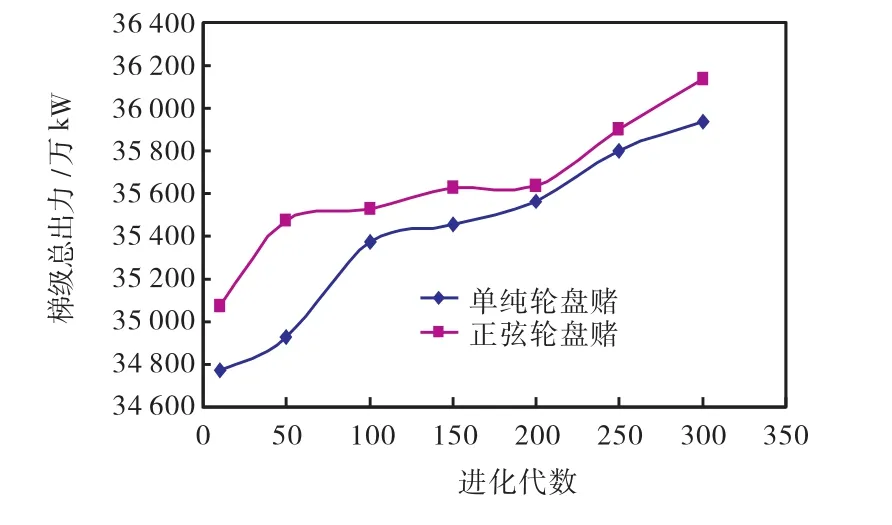
图1 两种选择方式在不同进化代数下的出力对比Fig.1 Comparison of output between two selection modes in different evolutionary generation

单独选取进化代数为300作为终止条件下，将2种算法求得的最优解进行对比分析．正弦轮盘赌选择算子最好的一次调度出力分配见图2和图3，单纯轮盘赌选择算子最好的一次调度出力分配见图 4和图 5．

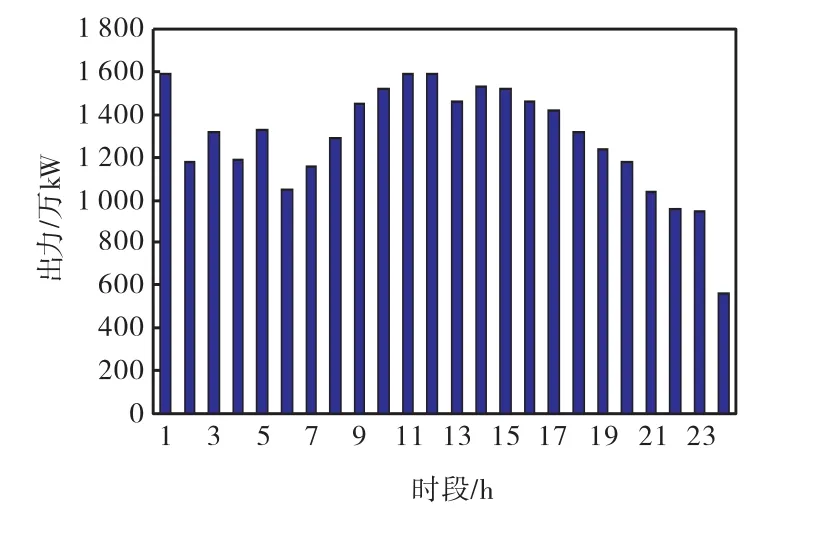
图2 正弦轮盘赌三峡出力分配Fig.2 Sine-roulette Three Gorges output distribution

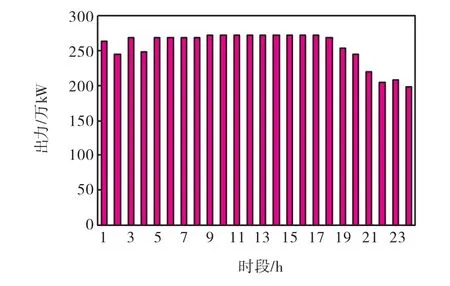
图3 正弦轮盘赌葛洲坝出力分配Fig.3 Sine-roulette Gezhouba output distribution

在进化300代的条件下，采用正弦轮盘赌计算出的24,h梯级水库最大出力和为36,990.0万kW，其中三峡出力 30,855.3万 kW，葛洲坝出力 6,134.7万kW；而单纯轮盘赌计算的 24,h最大出力和为36,970.1万kW，其中三峡出力30,854.8万kW，葛洲坝出力6,115.3万kW．从优化调度的过程可以看出，改进后的选择算子计算结果相对较好，能够以较快速度收敛．

图4 单纯轮盘赌三峡出力分配Fig.4 Simple roulette Three Gorges output distribution

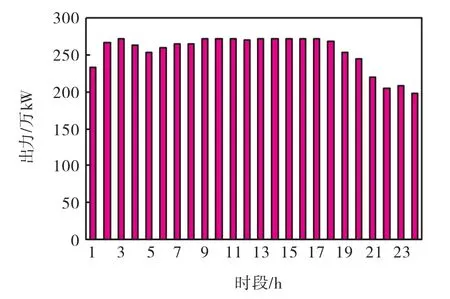
图5 单纯轮盘赌葛洲坝出力分配Fig.5 Simple roulette Gezhouba output distribution

文献[7]中曾提到基于三角函数轮盘赌选择在进化初期不如单纯轮盘赌算法．原因可能是由于三角函数在对适应值进行非线性变换的时候相当于加入了噪声，且这种处理方法可能在进化初期产生影响．但在进化后期，改进后选择明显优于单纯轮盘赌选择，这一点在图 1中得到了很好的证明．因此三角函数这种对适应值加入噪声的处理方式并没有改变全局最优解．文献[7]中提到的初期进化效果不好，是在进化代数相当小的情况下出现的．本研究特意在进化 10代的前提下模拟调度，证明了该进化代数下选用三角函数选择算子进行水库群优化调度的结果好于单纯轮盘赌．对于水库群优化调度问题，相当小进化代数下，只能得到局部最优解，因此研究相当小进化代数下的调度没有实际意义．因此，对求解水库群优化调度问题，正如文献[7]提到的当个体有重复情况出现的时候，三角函数选择算子能够更好地保持种群多样性，从而增大收敛速度，在进化后期容易找到全局最优解；当遇到个体无重复的情况，三角函数选择算子可避免单纯轮盘赌选择算子在消除重复个体上消耗的时间，可提高算法的效率，因此该选择算子在求解水库群优化调度问题上有很好的实用性．

4 结 语

作为优化搜索方法，GA为水库优化调度带来了新的思路．但是由于选择机制对适应度函数依赖较高，而水库优化调度问题的很多约束往往不能保证适应值非负，因此传统的选择算子均有其局限性，导致GA早熟．而本文提出的改进算法，在AGA的基础上进行，由于采用三角函数对适应值进行了非线性转化，且这种加入噪声的做法并没有改变全局最优解，故能够在选择过程中有效地保持种群的多样性，很好地避免GA的早熟，为遗传算法的改进提供新的思路．

本研究在模型的建立上，以库群调度为实例，更具有说服力．梯级间水力联系的计算，尤其是非恒定流的计算，涉及到梯级中各水电站水头、流量和水量平衡等，是十分复杂的问题，还没有系统成熟完善的处理方法．对于上游水电站出流与下游水电站相应入流具有密切相关关系的水电站群间流量传播的计算问题，本文提出的流量时空演变相关分析法，为梯级间水力计算提供一个可行方向．

［1］ 王小平，曹立明. 遗传算法：理论、应用与软件实现[M]. 西安：西安交通大学出版社，2002.

Wang Xiaoping，Cao Liming. Genetic Algorithms：Theory，Application and Implementation[M]. Xi’an：Xi'an Jiaotong University Press，2002(in Chinese).

［2］ 马光文，王 黎. 遗传算法在水电站优化调度中的应用[J]. 水科学进展，1997，8(3)：275-280.

Ma Guangwen，Wang Li. Application of genetic algorithm to optimal operation of hydropower station[J]. Advances in Water Science，1997，8(3)：275-280(in Chinese).

［3］ 王大刚，程春田，李 敏. 基于遗传算法的水电站优化调度研究[J]. 华北水利水电学院学报，2001，22(1)：5-10.

Wang Dagang，Cheng Chuntian，Li Min. Study on the optimal operation of hydropower station based on genetic algorithms[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power，2001，22(1)：5-10(in Chinese).

［4］ 王少波，解建仓，孔 珂. 自适应遗传算法在水库优化调度中的应用[J]. 水利学报，2006，37(4)：480-485.

Wang Shaobo，Xie Jiancang，Kong Ke. Application of adaptive genetic algorithm in optimization of reservoir operation[J]. Journal of Hydraulic Engineering，2006，37(4)：480-485(in Chinese).

［5］ 梅亚东，朱教新. 黄河上游梯级水电站短期优化调度模型及迭代解法[J]. 水力发电学报，2002(2)：1-7.

Mei Yadong，Zhu Jiaoxin. Short-term optimal operation model for the cascade hydroelectric stations on the upper yellow river and its solution[J]. Journal of Hydroelectric Engineering，2002(2)：1-7(in Chinese).

［6］ 宋朝红，罗 强，纪昌明. 基于混合遗传算法的水库群优化调度研究[J]. 武汉大学学报：工学版，2003，36(4)：28-31.

Song Chaohong，Luo Qiang，Ji Changming. Hybrid genetic algorithm-based optimal operation of reservoirs system[J]. Engineering Journal of Wuhan University，2003，36(4)：28-31(in Chinese).

［7］ 郝国生，严玉若，黄永青，等. 基于三角函数的遗传算法选择算子[J]. 江南大学学报，2010，9(2)：162-165.

Hao Guosheng，Yan Yuruo，Huang Yongqing，et al.Trigonometric selective operators in genetic algorithm[J]. Journal of Jiangnan University，2010，9(2)：162-165(in Chinese).

［8］ Zalzala A M，Fleming P J. Genetic Algorithms in Engineering System[M]. London：The Institution of Electrical Engineers，1997.

［9］ 吴 斌，吴 坚，涂序彦. 快速遗传算法研究[J]. 电子科技大学学报，1999，28(1)：49-53.

Wu Bin，Wu Jian，Tu Xuyan. Research of fast genetic algorithm[J]. Journal of UEST of China，1999，28(1)：49-53(in Chinese).

［10］ 张 慧. 遗传算法在水电站群经济运行中的应用[D].南京：河海大学水文水资源学院，2007.

Zhang Hui. Application of Genetic Algorithm in Multi-Hydropower-Station Economical Operation System[D].Nanjing：College of Hydrology and Water Resources，Hohai University，2007(in Chinese).

［11］ 杨 侃，刘云波. 基于多目标分析的库群系统分解协调宏观决策方法研究[J]. 水科学进展，2001，12(2)：232-236.

Yang Kan，Liu Yunbo. System decompositioncoordination macro-decision method for reservoirs based on multi-objective analysis[J]. Advances in Water Science，2001，12(2)：232-236(in Chinese).