双馈风力发电机混合粒子群优化设计

王慧敏，夏长亮, ，乔照威，宋战锋

(1. 天津大学电气与自动化工程学院，天津 300072；2. 天津工业大学电气工程与自动化学院，天津300387)

发电机将机械能转换为电能，是风力发电系统重要组成部件之一，其性能优劣直接影响系统的整体性能．双馈发电机因具有功率调节灵活、励磁容量小、性价比高等优点，成为变速恒频风电系统的主流机型[1]．因此，双馈风力发电机的优化设计对风电技术进步和产业发展具有重要意义．

电机电磁计算准确度直接关系到优化结果的可靠性．双馈风力发电机转子采用交流励磁，且应用于变速恒频风力发电领域，其电磁关系及运行特性较为特殊．文献[2]探讨了双馈发电机因转子交流励磁而产生的电磁关系特性及设计特点．文献[3-4]结合风电系统运行特性，定性分析了双馈发电机设计指标选取原则和部分电磁计算方法．

粒子群优化(particle swarm optimization，PSO)算法是一种模仿鸟类群体行为的智能优化算法[5]，因其思想直观、实现简单且具有很高的执行效率，逐步用于多个实际工程领域[6]．为了提高粒子群算法的寻优性能，文献[7]采用随时间线性递减的惯性权重，使得算法前期具有较高的全局搜索能力，后期具有较高的局部搜索能力，加快了收敛速度；在此基础上，文献[8]利用模糊控制器调节惯性权重，动态平衡全局和局部搜索能力．文献[9]考虑各粒子适应度值的影响，对同一代的不同粒子采用不同的惯性权重，以改善算法性能．文献[10]提出 AR粒子群算法，通过引入“吸收”和“扩散”算子，一定程度上解决了算法易过早收敛的问题．文献[11]对比分析了多种“变异”操作，研究结果表明变异操作有利于避免算法陷入局部最优．

笔者在分析双馈风力发电机电磁设计特点的基础上，以有效材料成本、额定效率和效率曲线平坦性为目标建立电机优化设计模型，进而提出一种混合粒子群优化算法，通过引入基于适应度值的个体模糊权重和基于种群多样性的自适应变异，提高算法处理多峰值非线性优化问题的能力，实现双馈风力发电机优化设计．

1 双馈风力发电机优化设计模型

1.1 双馈风力发电机电磁设计特点

假定定子侧采用发电机惯例，转子侧采用电动机惯例，且转子侧各量均折算至定子侧，并忽略激磁电阻，可得双馈风力发电机基本方程为

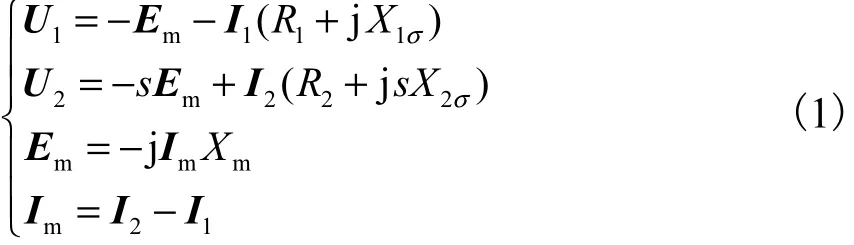
式中：1U、2U分别为定、转子相电压矢量；mE 为感应电动势矢量；1I、2I、mI分别为定、转子相电流和激磁电流矢量；R1、R2分别为定、转子电阻；X1σ、X2σ、Xm分别为定、转子漏电抗和激磁电抗；s为转差率．

忽略定、转子电阻及漏抗上的压降，并经过绕组折算，由式(1)推得双馈风力发电机转子电压实际值，即功率变换器输出电压为

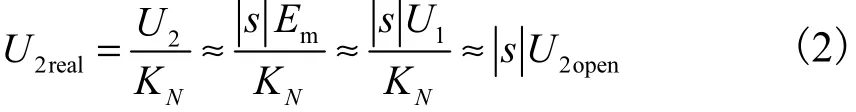
式中：KN为定、转子绕组每相有效串联匝数比；U2open为转子开路电压．

由式(2)可以看出，功率变换器输出电压近似为转子开路电压与转差率绝对值的乘积，因此双馈风力发电机设计时转子开路电压需与功率变换器电压等级及发电机运行转速范围相匹配．同时，为了减小功率器件电流等级以降低成本，设计倾向于较大的转子电压和较小的转子电流，即转子开路电压在不影响励磁控制稳定性前提下尽可能取较大值．

将转子电压方程两端同乘以 3倍转子电流共轭矢量，分别取实部及虚部推得转子功率方程为

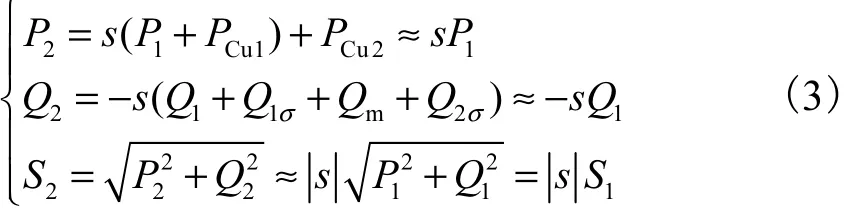
式中：P1、Q1和 S1分别为定子输出有功、无功和视在功率；P2、Q2和 S2分别为转子输入有功功率、无功功率和转子容量；PCu1、PCu2分别为定、转子铜耗；Q1σ、Q2σ和 Qm分别为定、转子漏抗和激磁电抗消耗无功功率．

由式(3)可以看出，转子容量与转差率绝对值成正比，运行转速范围越宽，所需功率变换器容量越大，双馈风力发电系统经济成本越高．而运行转速范围越宽，风电系统转换的风能就越多，经济收益越好．同时，由于系统在额定转速以上采用恒功率输出控制策略，发电机转速范围增加时总输出功率保持不变，使得功率变换器容量增加所付出的成本代价更大．因此，双馈风力发电机设计时，在折中选择发电机运行转速范围的同时，需要考虑额定转速的影响，以达到较好的经济性能指标．

双馈风力发电机运行转速范围较宽，最大转差率达 30%左右．因转子电流频率与转差率绝对值成正比，转子铁心内交变磁化的频率比普通绕线式异步电机高得多，因此双馈风力发电机转子铁心损耗不应忽略．不考虑磁路饱和程度影响，转子铁耗估算方程为

式中：KFet、KFej分别为转子齿部、轭部铁耗校正经验系数；p1/50为1,T磁密和50,Hz频率下铁心材料单位损耗；B2t、B2j分别为转子铁心齿部、轭部磁密；G2t、G2j分别为转子铁心齿部、轭部重量．

由异步电机转子反应可知，双馈发电机运行过程中气隙内的主磁通基本不变，即转子铁心各部分磁密保持不变．由式(4)可以看出，不同于定子铁耗，双馈风力发电机转子铁耗与转差率绝对值成正比，将随着转速变化而变化，属于可变损耗．

计及上述电磁设计特点，双馈风力发电机电磁计算流程如图1所示．

图1 双馈风力发电机电磁计算流程Fig.1 Flow chart of DFIG electromagnetic calculation

由图1中可以看出，双馈风力发电机电磁计算流程分为尺寸计算、磁路计算和性能计算 3部分．不同于普通异步电机，双馈风力发电机磁路计算中，电势系数迭代环节内部嵌套有功功率迭代环节，而性能计算中，额定效率直接计算得到，省去了效率迭代环节．此外，双馈风力发电机电磁计算流程中包含多个非线性不等式约束，当任意一个约束条件不满足时，应立即结束本次计算，表明设计方案不符合要求，需要进行调整．

1.2 双馈风力发电机优化设计模型

考虑风力发电应用领域特点和要求，分别选取电机有效材料成本、额定效率及效率曲线平坦性为优化目标，相应的目标函数分别表示如下．

1) 有效材料成本函数 fC(x)

式中：CCu、CFe分别为铜、铁材料单价；GCu、GFe分别为双馈风力发电机铜、铁有效材料质量．选择有效材料成本函数作为优化目标，可以降低双馈风力发电机成本，提高风力发电系统的投资收益比．

2) 额定效率函数 fη(x)

式中 ηN为双馈风力发电机额定效率．因额定效率最优是额定效率的最大化，本文将额定效率函数取为额定效率的负值，将其转化为最小化问题．选择额定效率函数为优化目标，可以提高双馈风力发电机额定运行时的效率，增加风力发电系统的收益．

3) 效率曲线平坦性函数 fΔη(x)

式中 ηmax、ηmin分别为双馈风力发电机在最大和最小转速下的运行效率．由于在整个运行转速范围内，双馈风力发电机效率是转速的单调递增函数，因此本文将效率曲线平坦性函数表示为最大与最小转速下效率的差值，该差值越小，表明效率曲线越平坦．选择效率曲线平坦性函数为优化目标，可以提高双馈风力发电机中、低速段的运行效率，增加总的电能输出，提高系统整体效率．

按几何参数开槽可以减少电磁计算时间，避免因按电磁参数开槽引起的死循环．为了配合该种开槽方法，本文并不直接取定、转子槽形尺寸作为优化变量，而是将双馈风力发电机优化变量取为

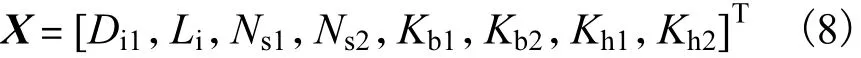
式中：Di1为定子铁心内径；Li为铁心长；Ns1、Ns2分别为定、转子每槽导体数；Kb1、Kb2分别为定、转子槽上部宽与齿宽之比；Kh1、Kh2分别为定、转子槽身高与轭高之比．

双馈风力发电机优化设计的约束条件主要是指电机的技术性能要求和制造工艺限制，大体分为3类约束，分别是：尺寸结构约束，如槽满率、槽形尺寸范围等；电磁指标约束，如定、转子磁通密度，定、转子电流密度等；性能指标约束，如转子开路电压、短路电流冲击倍数及定子电压波形畸变率等．此外，当选择上述3个目标函数中的任意一个为优化目标时，其他2个目标函数需当作约束条件处理，确保优化结果的有效性．

双馈风力发电机优化设计模型如图2所示．

由图2中可以看出，双馈风力发电机优化设计模型中，电磁计算程序以优化变量为输入量，优化目标为输出量，通过电磁计算建立优化变量和优化目标之间的非线性关联，从而作为子程序被优化算法主程序调用．同时，采用罚函数法处理约束条件，即在每次电磁计算过程中，当某一约束条件不满足时，立即停止本次计算，并将标志位Flag置零，表示电磁计算失败，该组优化变量不是优化设计的可行解；反之，若所有的约束条件均符合要求，则待本次计算完成后，将标志位 Flag置 1，表示电磁计算成功，该优化变量是可行解；当且仅当电磁计算成功时，优化目标才被优化算法接受，否则算法重新更新优化变量，并再次进行电磁计算．

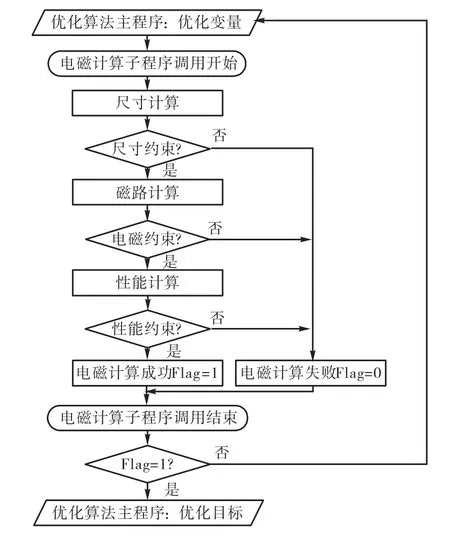
图2 双馈风力发电机优化设计模型Fig.2 DFIG optimum electromagnetic design model

2 混合粒子群优化算法

2.1 标准粒子群优化算法

在粒子群优化算法中，每个粒子都有自己的位置、速度和由目标函数决定的适应度值，并根据“自身经验”和“种群经验”在搜索空间中向更好的位置聚集，搜索最优解．标准粒子群优化算法粒子更新方程为

式中：k表示迭代次数；i表示粒子编号(i＝1，2，…，m，m 为群体规模)；d表示第 d维优化变量(d＝1，2，…，n，n为优化变量维数)；v为粒子速度；x为粒子位置；PB是粒子个体极值点；GB是种群全局极值点；ω为惯性权重；c1为认知系数；c2为社会系数；r1、r2为[0，1]之间的随机数．

通常惯性权重ω为线性递减函数，即

式中：k为当前迭代次数；Niter为最大迭代次数；ωmax和ωmin分别为惯性权重的最大值和最小值．

2.2 基于适应度值的个体模糊惯性权重

在寻优过程中，每个粒子所承担的搜索任务应不相同．以最小化问题为例，粒子适应度值越小，在该粒子周围区域发现全局最优的概率越大，该粒子应在其周围局部区域内进行精细搜索，因而需要相对较高的局部搜索能力；而粒子适应度值越大，该粒子应探索越广的区域，承担较大范围的搜索任务，因而需要较高的全局搜索能力．因此，对同一代的不同粒子应采用不同的惯性权重，即个体惯性权重，以提高粒子群算法的收敛速度．

在寻优过程中，由于粒子搜索行为是复杂且非线性的，将其近似看成一个从全局搜索到局部搜索的线性变化过程并不能很好地满足搜索需求，因此混合粒子群优化算法将模糊控制器用于个体惯性权重的调节过程，通过自适应地改变粒子惯性权重，动态平衡全局与局部搜索能力．为了提高算法通用性，将粒子适应度值fi转化为规范化形式fi*，即

式中：fGB为种群全局极值点的适应度值；favg为种群适应度值均值，

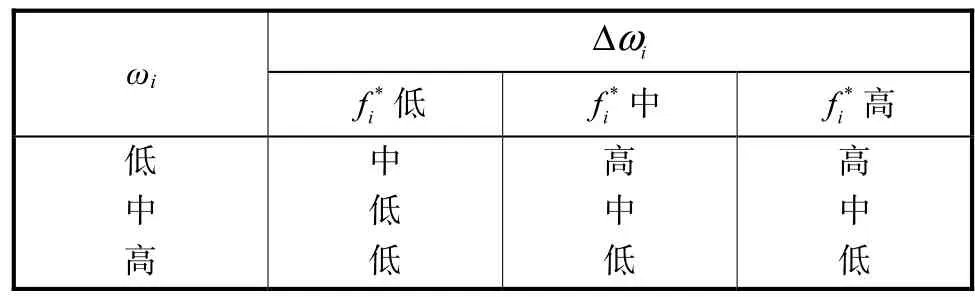
表1 模糊规则Tab.1 Fuzzy rules

综上，采用基于适应度值的个体模糊权重后，混合粒子群算法粒子速度更新方程为

2.3 基于种群多样性的自适应变异

粒子群优化算法在处理多峰值非线性优化问题时，由于种群多样性随着迭代次数增加而逐渐丧失，粒子有陷入局部最优的可能．针对这一问题，本文提出了基于种群多样性的自适应变异操作，令变异概率和变异算子随种群多样性状况变化而变化，以维持种群在整个寻优过程中具有合理的多样性，保证算法收敛的同时避免陷入局部最优．

将种群多样性函数定义[10]为

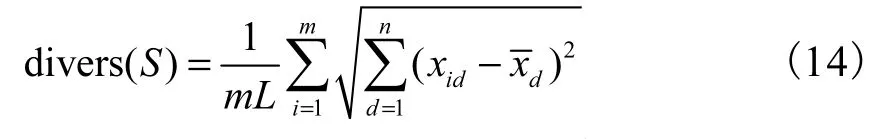
式中：S为粒子群；xd为m个粒子的第d维优化变量平均值；L为搜索空间最长半径，即

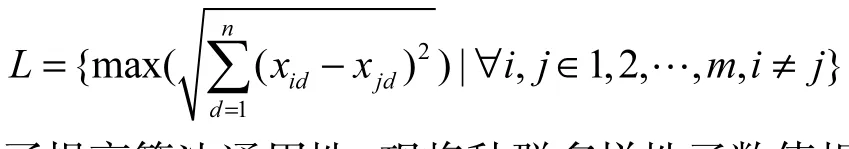
为了提高算法通用性，现将种群多样性函数值规范化处理，即

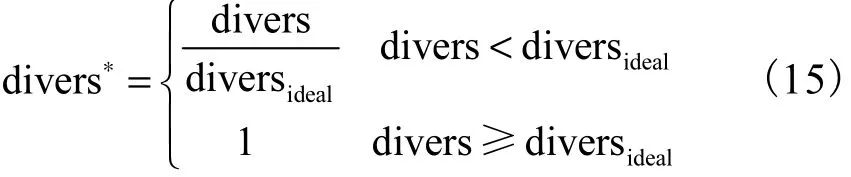
式中：divers*为规范化的种群多样性函数值；divers为当前种群多样性函数值；diversideal为种群多样性函数理想值，表示此时种群多样性状况较为理想．

对于复杂多峰值非线性优化问题，过多的粒子进行变异将会影响算法的收敛，而过少的粒子进行变异将无法维持种群拥有足够的多样性，导致粒子易陷入局部最优．为此，在迭代过程中，令变异概率随种群多样性状况自适应变化，当种群多样性较低时，采用较大的变异概率，阻止粒子陷入局部最优；随着种群多样性状况的逐步改善，算法逐步采用相对较小的变异概率，相应地减少进行变异的粒子数目；当种群多样性函数值高于理想值时，表明种群多样性状况理想，甚至算法有发散的趋势，不需要有粒子进行变异，算法采用的变异概率为零．根据上述分析，令变异概率为

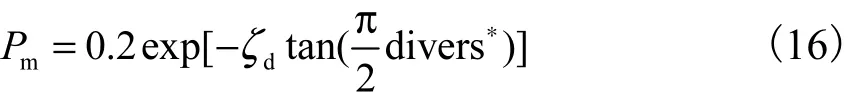
式中ζd为种群多样性对变异概率的影响因子．

同理，当种群多样性较低时，粒子应该在较大的范围内进行变异，以跳出局部最优；当种群多样性较高时，粒子应该在较小的范围内进行变异，以保持向最优位置收敛．同时，为了保证粒子群算法收敛，随着迭代次数的增加，粒子的搜索范围逐渐减小，粒子变异范围也应随之减小．

基于上述分析，采用变异算子

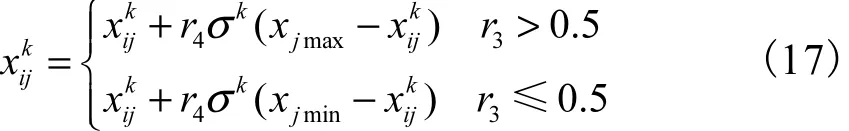
其中

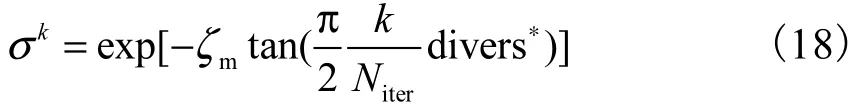
式中：r3、r4为[0，1]内均匀分布的 2个随机数；σ为变异幅度因子，表示粒子变异范围的相对大小；ζm为种群多样性对变异幅度的影响因子．

综上所述，混合粒子群优化算法流程如图3所示.

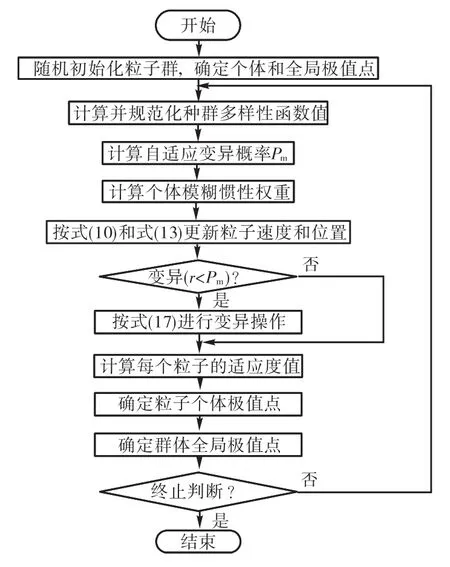
图3 混合粒子群优化算法流程Fig.3 Flow chart of the HPSO algorithm

3 优化设计实例分析

以电机有效材料成本、额定效率及效率曲线平坦性为优化目标，分别利用标准粒子群(SPSO)算法和混合粒子群(HPSO)算法进行 15 kW 双馈风力发电机优化设计，其中 2种算法群体规模均为 20个粒子，最大迭代次数为 800次，惯性权重范围为[0.4，0.9]；混合粒子群算法参数 ζd＝0.5，ζm＝2，为多次测试值；优化前电机原始设计方案借鉴于 YR180M-4绕线式异步电机技术数据．

根据风力发电国家标准和行业要求，制定15 kW双馈风力发电机主要技术指标如表2所示．

表2 15 kW双馈风力发电机技术指标Tab.2 Technical indexes of the 15 kW DFIG design

15 kW 双馈风力发电机优化设计主要约束条件如表3所示．

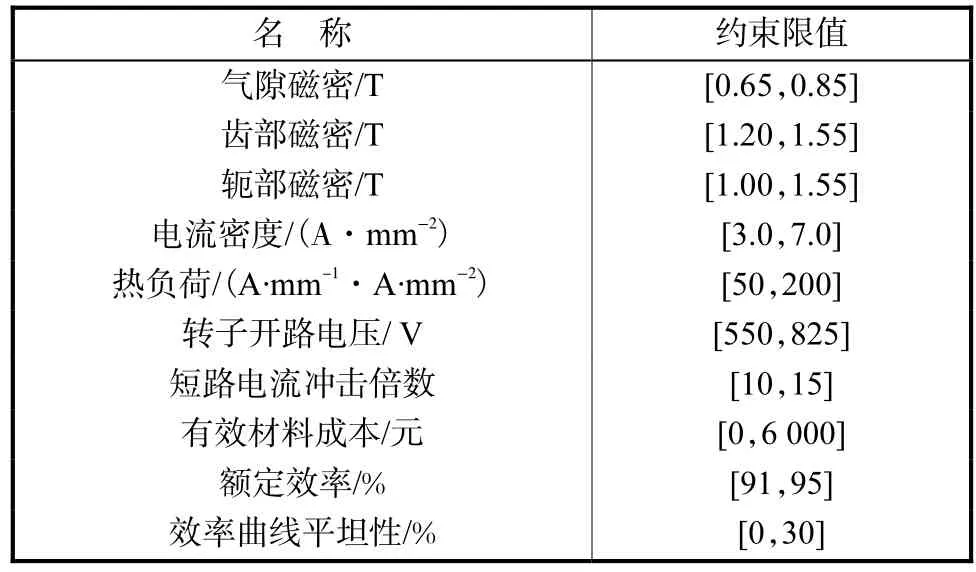
表3 15 kW双馈风力发电机主要约束条件Tab.3 Constraints used in the 15 kW DFIG optimum design

表4为分别以有效材料成本、额定效率和效率曲线平坦性为优化目标时的双馈风力发电机优化设计结果．

由表4中粗体数据可以看出，与标准粒子群算法相比，无论是以有效材料成本、额定效率还是效率曲线平坦性为优化目标，混合粒子群算法均获得了目标值较优的设计方案，表明混合粒子群算法基本克服了标准粒子群算法处理多峰值优化问题时易陷入局部最优的缺点，寻优精度较高，寻优效果较为稳定，较好地实现了双馈风力发电机优化设计．

为了更直观地反映混合粒子群算法的寻优性能，图4给出了双馈风力发电机优化设计收敛曲线.

由图 4中可以看出，相比于标准粒子群算法，混合粒子群算法具有较快的收敛速度和较高的寻优精度，不易陷入局部最优，算法寻优性能得到较好地改善，双馈风力发电机优化设计结果较理想．

上述结果表明，混合粒子群优化算法较好地改进了标准粒子群算法的不足，寻优性能进一步提升，收敛速度较快，寻优精度较高，可以较好地实现双馈风力发电机优化设计，为此类多峰值优化问题提供了一种新的解决方法．

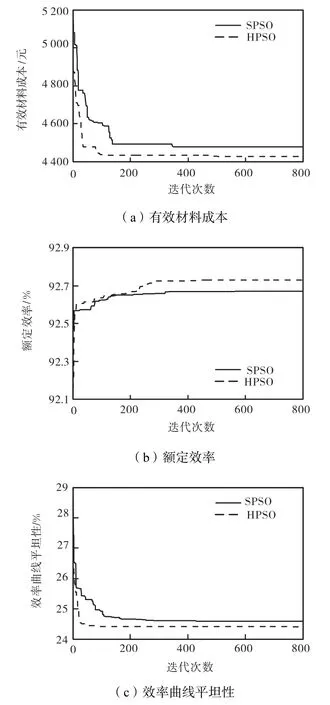
图4 双馈风力发电机优化设计收敛曲线Fig.4 Convergence curves of the DFIG optimum design

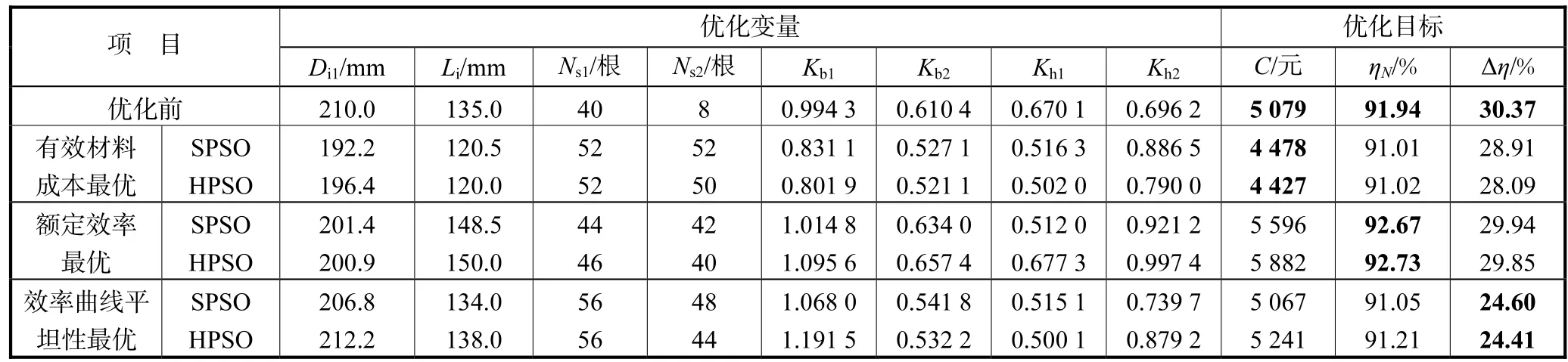
表4 双馈风力发电机优化设计结果Tab.4 Optimization results of the DFIG design

4 结 语

电机优化设计属于多峰值非线性优化问题，其目标函数和约束条件具有强非线性，往往存在多个局部最优解．对此，本文在分析双馈风力发电机电磁设计特点的基础上，分别选取电机有效材料成本、额定效率及效率曲线平坦性为优化目标，建立了电机优化设计模型，并提出了一种混合粒子群优化算法．该算法对同一代的不同粒子根据适应度值优劣模糊选择不同的惯性权重，并根据种群多样性状况自适应地确定变异概率和变异因子，增强了粒子群算法对双馈风力发电机优化设计的适用性．电机优化设计实例结果表明，与标准粒子群算法相比，混合粒子群算法可以动态平衡全局和局部搜索能力，收敛速度较快、寻优精度较高且不易陷入局部最优，可以较好实现双馈风力发电机优化设计，对于多峰值非线性优化问题具有一定的适用性．

［1］ 夏长亮，王慧敏，宋战锋，等. 变速恒频双馈风力发电系统空载并网积分变结构控制[J]. 天津大学学报，2008，41(11)：1281-1286.

Xia Changliang，Wang Huimin，Song Zhanfeng，et al.Integral variable structure controller for no-load cuttingin control of variable speed constant frequency windpower system with doubly-fed induction generator[J].Journal of Tianjin University，2008，41(11)：1281-1286(in Chinese).

［2］ 廖 勇，杨顺昌. 交流励磁发电机的电磁设计[J]. 重庆大学学报，1999，22(6)：47-53.

Liao Yong，Yang Shunchang. Design of alternating current excitation generators[J]. Journal of Chongqing University，1999，22(6)：47-53(in Chinese).

［3］ 杨 强，黄守道，高 剑. 兆瓦级交流励磁双馈风力发电机的电磁设计研究[J]. 大电机技术，2007(4)：23-28.

Yang Qiang，Huang Shoudao，Gao Jian. Study of electromagnetic design for MW-class AC-excited doubly-fed wind power generator[J]. Large Electric Machine and Hydraulic Turbine，2007(4)：23-28(in Chinese).

［4］ 魏静微，谭 勇，张宏宇. 大型交流励磁双馈风力发电机的设计[J]. 电机与控制学报，2010，14(5)：44-48.

Wei Jingwei，Tan Yong，Zhang Hongyu. Design of AC-excited doubly-fed wind power generator with large capacity[J]. Electric Machines and Control，2010，14(5)：44-48(in Chinese).

［5］ Eberhart R C，Kennedy J. A new optimizer using particle swarm theory[C]// Proceedings of the Sixth International Symposium on Micro Machine and Human Science. Piscataway，USA，1995：39-43.

［6］ Raj C T，Strivastava S P，Agarwal P. Realization on PSO based induction motor design via SPEED/PC-IMD[C]// International Conference on Advanced Computer Control. Singapore，2009：65-69.

［7］ Shi Yuhui，Eberhart R C. Empirical study of particle swarm optimization[C]// Proceedings of IEEE Congress on Evolutionary Computation. Washington，USA，1999：1945-1949.

［8］ Shi Yuhui，Eberhart R C. Fuzzy adaptive particle swarm optimization[C]// Proceedings of IEEE Congress on Evolutionary Computation. Seoul，Korea，2001：101-106.

［9］ 郭文忠，陈国龙. 粒子群优化算法中惯性权值调整的一种新策略[J]. 计算机工程与科学，2007，29(1)：70-72，75.

Guo Wenzhong，Chen Guolong. A new strategy of inertia weight adjustment for particle swarm optimization[J].Computer Engineering and Science，2007，29(1)：70-72，75(in Chinese).

［10］ Riget Jacques，Vesterstrom J S. A Diversity-Guided Particle Swarm Optimizer-the ARPSO[R]. Denmark：Aarhus University，2002.

［11］ Stacey Andrew，Jancic Mirjana，Grundy Ian. Particle swarm optimization with mutation[C]// IEEE International Congress on Evolutionary Computation. Piscataway，NJ，USA，2003：1425-1430.