二维介质粗糙面下方三维金属目标复合电磁散射的快速正演算法

李 超，何思远＊，朱国强，邓方顺，陶 华，肖柏勋

1 武汉大学电子信息学院，武汉 430079

2 中国船舶重工集团第722研究所，武汉 430079

3 中国人民解放军92474部队

4 长江大学工程地球物理研究中心，湖北荆州 434023

1 引 言

目标与粗糙面复合电磁散射研究在雷达目标探测、目标识别以及微波遥感等领域有着广泛的应用[1-20］.求解粗糙面上方或下方目标的电磁散射问题必须充分考虑目标与粗糙面之间的相互作用.Li等[1］提出用广义前后向迭代算法与谱加速算法结合（GFBM／SAA）计算海洋粗糙面上方目标的电磁散射场.Deng等[2］借助传统UV算法，结合分层思想，发展得到适用于三维矢量波散射问题的MLUV算法，并成功将其应用到目标位于粗糙面上方和目标位于粗糙面上时的复合散射问题.对于埋地问题，相关文献[3-4］用分层媒质并矢格林函数分析了平面分层大地中埋入目标的散射特性.在此基础上，Zhang等[5］引入离散复镜像技术（DCIM），加快了分层媒质并矢格林函数的计算，提高了计算效率.徐利明等[6］则利用积分方程以及半空间并矢格林函数的快速算法对埋地目标矢量电磁散射进行了计算.在一些埋入体散射问题中，需要计及大地表面起伏特性对散射场的影响.对于呈复杂曲面的地表面，埋入体的散射问题将变得更为复杂.为求解该类问题，一些文献采用基于矩量法的快速算法计算粗糙地面埋入体的电磁散射问题，如El-Shenawee等[7-8］采用最陡下降的快速多级子方法（SDFMM），Zhang等[9］则采用了稀疏矩阵正则网格（SMCG）算法.

本文基于矩量法，在粗糙面和埋地目标分别建立电场积分方程和PMCHW方程，结合MLUV算法，求解粗糙地面下方具有任意表面金属目标的电磁散射问题.三维多层UV方法[2］适用于三维矢量波散射问题的精确数值算法，其基于电磁相互作用的排序抽样算法有效解决了因积分核震荡导致传统UV分解失效的问题，可实现任意形状三维导电和介质体目标散射问题的求解.且通过矩阵快速填充技术[10］，在内存和计算时间上的复杂度均可达到O（NlogN），其中N为未知量个数.

2 耦合积分方程

假设三维金属目标埋于二维粗糙面下方，如图1（截面图）所示.上半空间为空气，标记为区域1，下半空间为大地，标记为区域2.地表面为随机粗糙面.E1，H1为区域1中的电磁场，E2，H2为区域2中的电磁场，Ei，Hi表示入射场.区域1、2的电磁参数分别为ε1，μ1，ε2，μ2，粗糙面和目标表面法向向量分别为ns，no.下文中，时谐因子e-jωt省略.

图1 三维目标浅埋于二维粗糙面下方截面图Fig.1 Cross section of 3-D object buried under the rough surface ground

区域1中任意场点r处的总电磁场为

区域2中任意场点r处的总电磁场为

算子L和K形式如下：

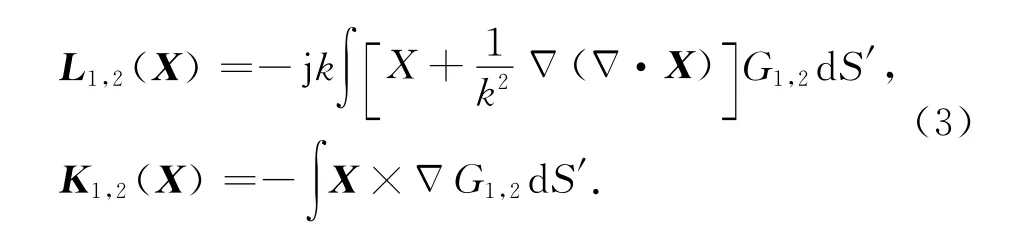
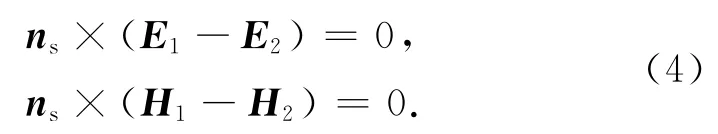
在PEC目标表面利用电场边界条件：

可得表面积分方程如下：

在粗糙面表面：

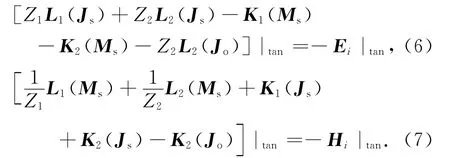
在PEC目标表面：

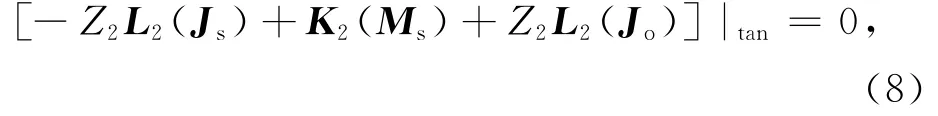
使用 RWG 基函数f（r）[21］将表面等效电流、磁流离散，假定粗糙面和目标表面离散后的未知量个数分别为N和P，其展开式如下：

将式（9）分别带入积分方程（6～8），并使用伽略金（Galerkin）方法，可得到离散后的矩阵方程组：

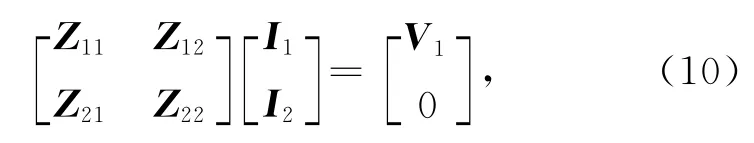
其中I1，I2为分别存在于粗糙面和目标上的未知量，两者对应的维数为2 N×1，P×1.

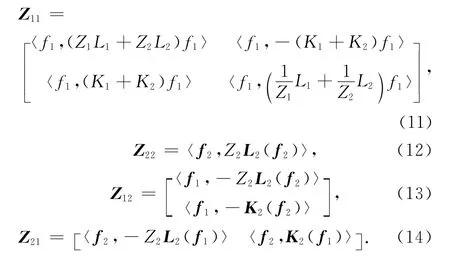
方程（10）将采用Bicgstable（ell）[22］迭代算法进行求解.

3 MLUV算法

对未知量为N的矩阵方程，传统矩量法对内存的需求为O（N2），其中N为未知量个数，求解矩阵方程的计算复杂度为O（N3）.多层UV方法基于低秩矩阵分解技术，通过将原有矩阵分解为具有强相互作用的强子块矩阵和弱相互作用的弱子块矩阵，并根据矩阵元素的Green函数的性质，将每个弱子块矩阵分解为两个小矩阵相乘的形式.这里以一个大小为m×n的远区弱子块矩阵A为例说明UV方法的具体实施过程：

（1）使用文献[10］提出的矩阵快速填充方法计算远区弱子块矩阵A，并计算其行和列对应的二阶范数向量Rl2和Cl2；

（4）根据列索引SC，从中抽取相应的s列构成列矩阵使用揭示秩的矩阵正交三角分解（QR分解）对ACm×s作 QR 分 解，即其中为矩阵的秩；

（5）根据行索引Sr，从和中抽取相应的s行构成行矩阵，求解矩阵方程，

通过以上的步骤，矩阵A可以分解成A=Um×r·Vr×n.从这里可以看出，通过UV分解处理后，实际需要存储的矩阵元素为r×（m+n），此外，在迭代过程，通过先将矩阵Vr×n与迭代中间值相乘后再与Um×r矩阵相乘实现矩阵向量积（Matrix Vector Multiplication），这样即可减小计算复杂度.

4 数值计算与讨论

取粗糙面为高斯谱粗糙面，相关长度lx，ly，均方根高度h，长度为Lx×Ly，金属球位于粗糙面下方，半径为R，埋地深度为dp，球体在xy面内投影坐标为 （xt，yt）.

为了消除数值计算中截取有限大小粗糙面产生的边缘效应，选用锥形平面波作为入射波.

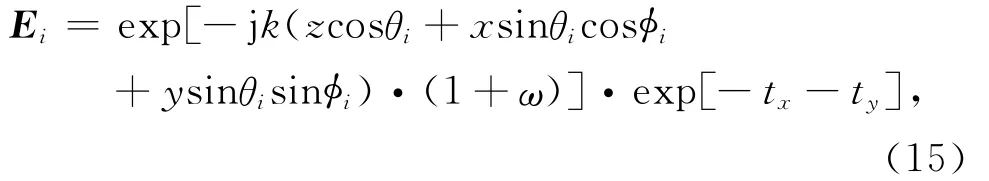
其中，

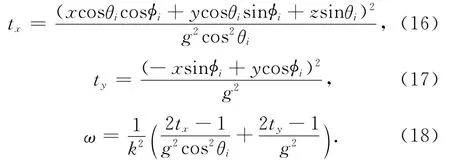
算法的验证：取 Lx=Ly=8λ0，lx=ly=0.5λ0，h=0.02λ0，粗糙面相对介电常数εr=2-0.2j，其中λ0为真空中电磁波波长.金属球半径0.3λ0，埋地深度为0.6λ0，xt=yt=0.入射波采用水平极化，入射俯仰角θi=20°，锥型波因子g=Lx／4.方位角取为0°，36°，…，324°共10个，分为10次实现，并采用算数平均值统计.图2为3DMLUV算法和SDFMM算法及MOM计算结果比较，验证了3DMLUV的精度.

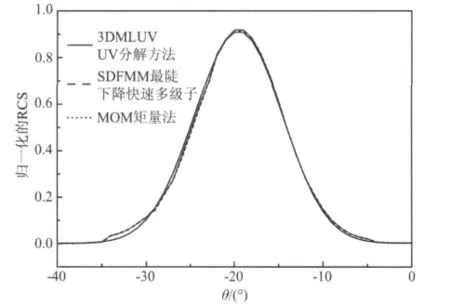
图2 埋地金属球双站RCS结果Fig.2 Bistatic RCS of PEC sphere buried under rough surface

在表1中，记录了在一次实现情况下，程序耗用的计算时间和内存.由表可知，在3DMLUV框架下，不仅计算时间得到缩减，程序所需内存也大幅度降低.计算平台CPU为I7，主频为2.8GHz，内存2G.

表1 一次实现时内存和计算时间的比较Table 1 Memory and time requirements for one realization

埋入球体目标电尺寸参数变化对双站RCS的影响.取粗糙面参数为Lx=Ly=10λ0，h=0.02λ0，lx=ly=0.5λ0，粗糙面相对介电常数εr=2-0.2j，其中λ0为真空中电磁波波长.入射波采用水平极化，入射俯仰角θi=20°.所有计算结果均是对50个样本取算数平均值得到的.金属球半径分别为0.8λ0，1.2λ0，1.8λ0，埋地深度均为2λ0，xt=yt=0.相应的E面内双站RCS如图3所示.由图可知，随着圆柱半径的增大，目标与粗糙面的相互作用增强，双站RCS增大，尤其在镜面反射方向附近以外的很大范围内这一结论表现的尤为明显.

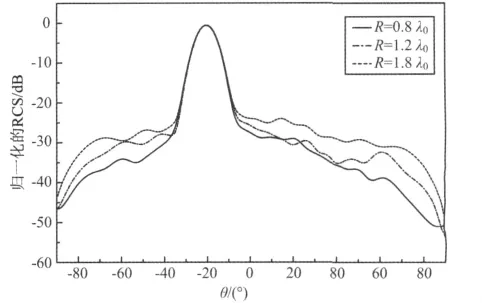
图3 粗糙面下不同半径球体对应的双站RCSFig.3 Bistatic RCS of PEC Sphere with different radius buried under rough surface

粗糙面参数对双站RCS的影响.其它计算参数保持不变，取粗糙面均方根高度分别为0.02λ0，0.03λ0，0.04λ0，此时，埋入球体半径固定为1.2λ0.图4为对应的双站RCS结果，其中图4a为E面内全角度双站RCS，图4b为镜向附近角度内双站RCS.由图可知，随着均方根高度的增大，除镜面反射方向附近一个小范围内RCS减小以外，其它散射角处RCS均增大.这是因为，随着粗糙度的增加，粗糙面漫反射现象越来越明显.

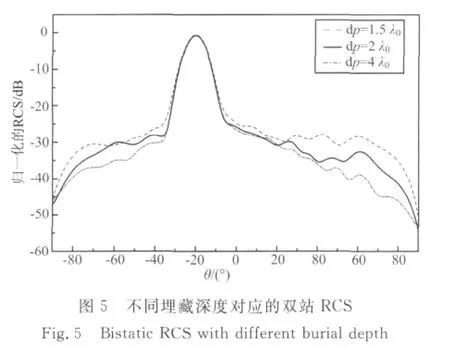
埋地深度变化对双站RCS的影响.其它参数保持不变，令球体埋藏深度取1.5λ0，2λ0，4λ0.对应的双站RCS如图5所示，由图可知，随着目标埋藏深度的增加，目标与粗糙面的距离增大，相互作用减弱，镜向反射方向外的RCS明显变小.

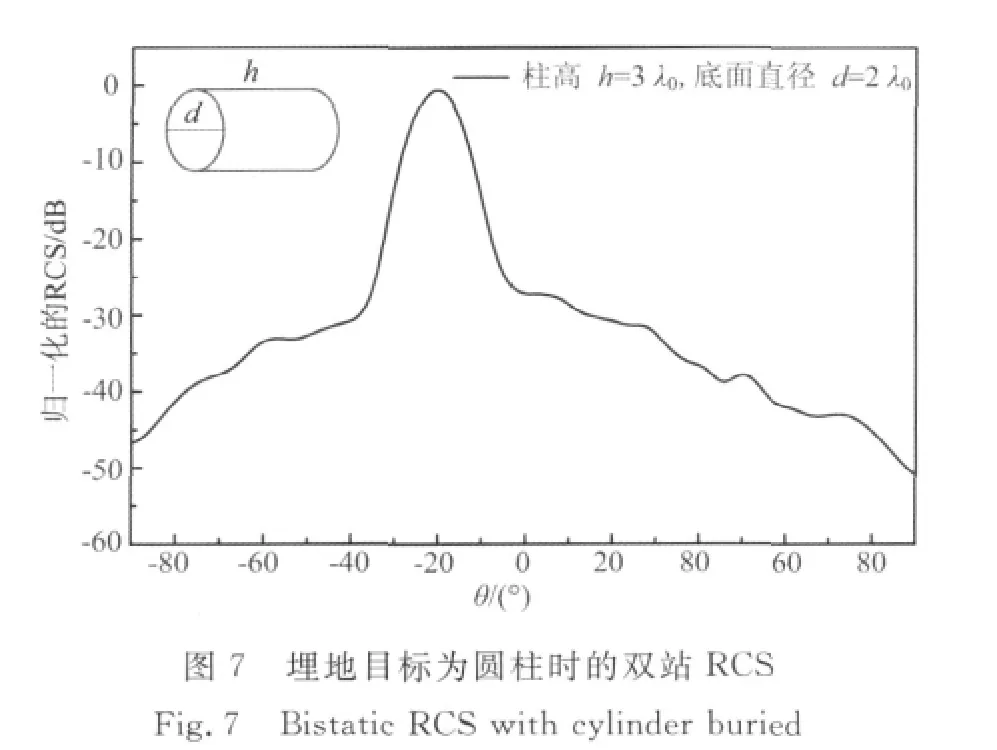
最后，图6为埋地目标为立方体时的双站RCS，立方体边长为2λ0，图7为埋地目标为圆柱时的双站RCS，立方体底面直径为2λ0，高度为3λ0，其它参数设置均保持不变.计算结果表明了算法的通用性.

5 结 语

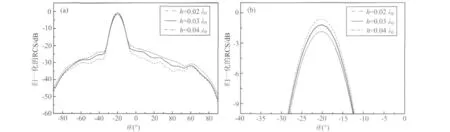
图4 粗糙面下方埋有球体时不同粗糙面粗糙度的双站RCS（a）E面内双站RCS；（b）镜面附近角度内双站RCS.Fig.4 Bistatic RCS of rough surface with different surface height while buried object is a sphere（a）Bistatic RCS in E-plane；（b）Bistatic RCS in specular angle.

本文基于MLUV算法计算了二维粗糙面下方任意形状金属目标的双站RCS.并通过分析金属球埋于粗糙面下方时，埋地目标电尺寸，粗糙面粗糙度以及埋地深度对双站RCS的影响.结果表明，随着目标尺寸增大和埋地深度的减小，目标与粗糙面的相互作用增强，RCS明显增大，反之则RCS减小.同时，粗糙面的粗糙度对RCS也有明显影响.最后，通过立方体和圆柱的算例表明了算法的通用性.

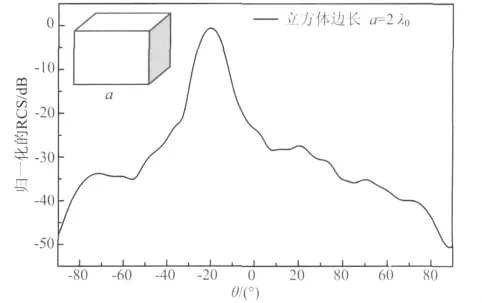
图6 埋地目标为立方体时的双站RCSFig.6 Bistatic RCS with cube buried

（References）

[1]Li Z X，Jin Y Q.Bistatic scattering from a fractal dynamic rough sea surface with a ship presence at low grazing angle incidence using the GFBM／SAA.Microw.Opt.Technol.Lett.，2006，31（2）：146-151.

[2]Deng F S，He S Y，Chen H T，et al.Numerical simulation of vector wave scattering from the target and rough surface composite model with 3-D multilevel UV method.IEEE Trans.Antennas Propagat，2010，58（5）：1625-1634.

[3]Cui T J， Wiesbeck W，Herschlein A.Electromagnetic scattering by multiple three-dimensional scatterers buried under multilayered media.II.Numerical implementations and results.IEEE Trans.Geosci.Remote Sensing，1998，36（2）：535-546.

[4]Cui T J，Chew W C.Fast evaluation of Sommerfeld integrals for EM scattering and radiation by three-dimensional buried objects.IEEE Trans.Geosci.Remote Sensing，1999，37（2）：887-900.

[5]Zhang Y H，Xiao B X，Zhu G Q.An improved weak-form BCGS-FFT combined with DCIM for analyzing electromagnetic scattering by 3-D objects in planarly layered media.IEEE Trans.Geosci.Remote Sensing，2006，44（12）：3540-3546.

[6]徐利明，聂在平.埋地目标体矢量电磁散射的一种快速正演算法.地球物理学报，2005，48（1）：209-215.Xu L M，Nie Z P.A fast forward algorithm for modeling vector electromagnetic scattering from buried dielectric objects.Chinese J.Geophys.（in Chinese），2005，48（1）：209-215.

[7]El-Shenawee M，Rappaport C，Mille M L，et al.Threedimensional subsurface analysis of electromagnetic scattering from penetrable／PEC objects buried under rough surfaces：Use of the steepest descent fast multipole method.IEEE Trans.Geosci.Remote Sensing，2001，39（6）：1174-1182.

[8]El-Shenawee M.The multiple interaction model for nonshallow scatterers buried beneath 2-D random rough surfaces.IEEE Trans.Geosci.Remote Sensing，2002，40（4）：982-987.

[9]Zhang G F，Tsang L，Pak K.Angular correlation function and scattering coefficient of electromagnetic waves scattered by a buried object under a two-dimensional rough surface.J.Opt.Soc.Am.A.，1998，15（12）：2995-3002.

[10]Chen H T，Luo J X，Zhu G Q.Using UV technique to accelerate the MM-PO method for three-dimensional radiation and scattering problem.Microw.Opt.Technol.Lett.，2006，48（8）：1615-1618.

[11]雷银照，马信山.均匀半空间导体的并矢格林函数解析式.地球物理学报，1997，40（2）：265-271.Lei Y Z，Ma X S.An analytical formljl of dyadic Green′s function for homogeneous half-space conductor.Chinese J.Geophys.（in Chinese），1997，40（2）：265-271.

[12]鲁来玉，张碧星，鲍光淑.电阻率随位置线性变化时的三维大地电磁模拟.地球物理学报，2003，46（4）：568-575.Lu L Y，Zhang B X，Bao G S.Modeling of three-dimensional magnetotelluric response for a linear Earth.Chinese J.Geophys.（in Chinese），2003，46（4）：568-575.

[13]闫沛文，童创明.基于FGMRES-FBTG算法的介质粗糙面散射特性的模拟.电波科学学报，2009，24（1）：115-119.Yan P W，Tong C M.Simulations of scattering characteristic of lossy dielectric surfaces based on FGMRES-PBTG method.Chinese Journal of Radio Science （in Chinese），2009，24（1）：115-119.

[14]Vitebskiy S，Carin L.Moment-method modeling of shortpulse scattering from and the resonances of a wire buried inside a lossy，dispersive half-space.IEEE Trans.Antennas Propagat.，1995，43（11）：1303-1312.

[15]Boix R R，Alexopóulos N G，Horno M.Efficient numerical computation of the spectral transverse dyadic Green′s function in stratified anisotropic media.J.Electromagn.Waves Appl.，1995，10（8）：1047-1083.

[16]Tran P，Maradudin A A.Scattering of a scalar beam from a two-dimensional randomly rough hard wall：Enhanced backscattering.Phy.Rev.B，1992，45（7）：3936-3939.

[17]Xiong Z H，Tripp A C.3-D electromagnetic modeling for near-surface targets using integral equations.Geophysics，1997，62（4）：1097-1106.

[18]Jandhyala V，Shanker B， Michielssen E，et al.Fast algorithm for the analysis of scattering by dielectric rough surfaces.J.Opt.Soc.Am.A，1998，15（7）：1877-1885.

[19]Chen Y H，Chew W C，Oristaglio M L.Application of perfectly matched layers to the transient modeling of subsurface EM problems.Geophysics，1997，62（6）：1730-1736.

[20]Thorsos E.The validity of the Kirchhoff approximation for rough surface scattering using a Gaussian roughness spectrum.J.Acoust.Soc.Am.，1988，83（1）：78-92.

[21]Rao S M，Wilton D R，Glisson A W.Electromagnetic scattering by surfaces of arbitrary shape.IEEE Trans.Antennas Propagat.，1982，30（3）：409-418.

[22]Topsakal E，Kindt R，Sertel K，et al.Evaluation of the BiCGSTAB（l）algorithm for the finite-element／boundaryintegral method.IEEE Trans.Antennas Propagation Magazine，2001，43（6）：124-131.