基于改进Krylov子空间算法的井中激电反演

李长伟，熊 彬，王有学，罗润林

桂林理工大学地球科学学院，桂林 541004

1 引 言

井中激发极化法，简称井中激电，作为在钻孔中进行激发极化测量的一种非常有效的地球物理勘探方法，在金属矿勘探中得到了越来越多的应用.井中激电反演包括了电阻率和极化率的反演，极化率数据的反演可以在电阻率反演的基础上得到[1-2］.有限元法由于其对复杂模型的处理能力，在地球物理电磁法模拟中得到广泛的应用[3-7］.通过将电位分解成正常电位和异常电位，Coggon[3］，Lowry等[8］给出了在正演模拟中能消去源点奇异性影响的异常电位法，Zhao等[9］进一步指出正常场的电导率应为点源处的电导率取值.借鉴异常电位法的思想，Pidlisecky等[10］在有限体积法的正演模拟中给出了消去边界效应和源点奇异性的右端项校正技术.对于有限元方程，由于其系数矩阵的对称正定阵性，常采用预处理共轭梯度法（PCG）求解[11-12］.Gauss-Newton法和共轭梯度法是求解反演优化问题的常用的方法，结合Krylov子空间算法，可以不进行Jacobian矩阵的存储，直接计算Jacobian矩阵向量积来实现迭代求解[13-14］.有限元法不要求规则的网格剖分，允许采用非结构化网格来离散模拟区域，Rücker等[15-16］采用非结构化网格实现三维电阻率有限元正反演，提高了对复杂模型的处理能力.

本文在正演模拟时，考虑到井眼影响，采用结构化和非结构化网格相结合的方式对模拟区域剖分.将右端项校正技术应用到有限元法的正演模拟中以减少边界效应和源点奇异性引起的误差.Krylov子空间法是求解大型稀疏线性方程组的常用方法.实际勘探中一般会采用多个点源电极布置，对应每个源电极位置都会形成一个有限元方程，从而形成了多个线性方程组.我们针对这多个线性方程组系数矩阵之间差异不大的特点，采用循环Krylov子空间算法提高多线性方程组的求解效率.反演采用粗网格剖分，用以降低反演问题的自由度和不适定性，正演网格在反演网格的基础上加密得到，以保证正演的计算精度.在反演迭代中，用不精确PCG算法近似求解模型修正量方程减少了计算量.根据刚度矩阵与电导率向量参数的线性关系，进一步简化了Jacobian矩阵向量积的计算公式，避免了存储刚度矩阵对电导率的显式求导过程.

2 正演问题

2.1 基本原理

2.1.1 点源场基本原理

地下稳恒电流产生的电场满足下面的微分方程[17］：

我们采用有限元方法进行正演模拟，对无限区域做截断处理，施加人工边界条件

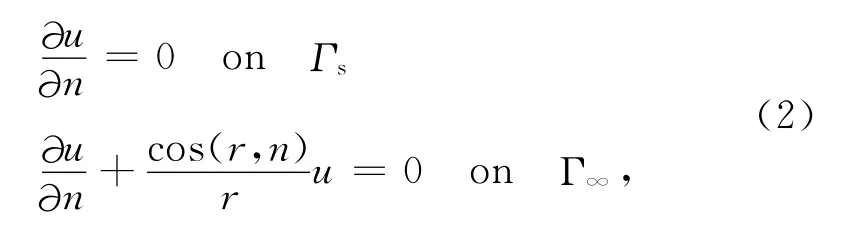
转化为变分问题[17］

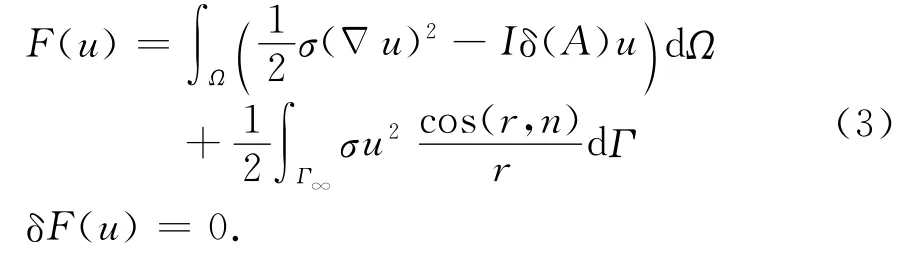
（3）中第一项是体积分项，第二项是边界积分项.其中r是点源到边界的距离，n是边界外法线方向.

用有限元方法对问题离散后得到线性方程组

（4）被称为有限元方程，其中K是离散正演算子，被称为刚度矩阵，u是节点电位未知量，eisrc是一个点源节点处分量为1，其它分量为0的向量，称为有限元方程的右端项.

2.1.2 视极化率的计算

用ρ表示电阻率，η表示极化率，ρs表示视电阻率，ηs表示视极化率，Δu，Δu1，Δu2分别表示极化场、一次场、二次场电位.根据Seigel理论[1］，等效电阻率为

视极化率为

在正演时，当求得一次场电位后，用等效电阻率代替相应的电阻率，再进行一次求解，便得到极化场电位，利用（6）式即可求得视极化率.

2.2 网格剖分

结构化网格的节点排列有序，每个节点和邻点的关系固定不变，网格生成速度快，数据结构简单，但是不能方便地进行局部网格加密.非结构化网格的节点编号命名并无一定规则，可以灵活地进行网格局部加密，能够有效地减少网格剖分单元.一般来说，井眼（直径为数十厘米）相对于整个剖分区域很小，对于这种窄狭区域，非结构化网格为了保证网格质量会导致大量的对提高精度意义不大的节点密集于这些区域，造成计算量的浪费和生成网格的困难[18］.因此在考虑井眼影响时，我们在井眼区域以井为中心采用放射状结构化网格，在外围区域采用非结构化网格剖分；若不考虑井眼影响时则对整个区域进行非结构化网格剖分.网格剖分见图1.

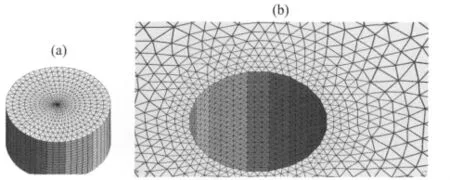
图1 网格剖分：井眼区域（a），外围区域（b）Fig.1 Finite element mesh：borehole（a），outside（b）

2.3 有限元方程的右端项校正

在人工截断边界上采用（2）式中的混合边界条件可在合理的计算范围内得到较高的正演模拟精度，但仍需要将边界选取在足够远的地方以减少边界效应的影响.此外，源点奇异性的存在造成源附近的模拟误差较大，异常电位法可以有效地降低源点奇异性引起的误差[8］.异常电位法得到的有限元方程为

式中us为异常电位，up为正常电位，u=up+us，σp为点源处的电导率值.设源节点的编号为s，若源点附近网格剖分足够精细，在所有包含点源节点的网格单元上有σp-σ=0，K（σp-σ）的第s行和第s列的元素均为0.

（7）式等价于

与原有限元方程相比，（8）式采用了新的右端项，能够补充正演算子由于边界取得不够远所丢失的信息，减少边界效应和源点奇异性引起的误差[10］.均匀半空间情况下有限元刚度矩阵K（σ）为pσp的线性函数，K（σp）up与σp的取值无关.

2.4 多线性方程组求解技术

实际的勘探工作往往涉及到多个点源电极布置，每一个点源位置对应不同的有限元方程，则需要求解多个线性方程组.考察变分问题（3），设点源个数为nsrc，将有限元方程（4）进一步写为

其中K0对应体积分项，ΔKj对应第j个点源的边界积分项.ΔKj是比K稀疏得多的低秩矩阵，将两项分开并分别进行存储，只需要存储K0和nsrc个ΔKj，可减少存储需求.

多线性方程组（9）的系数矩阵间只存在边界积分项的不同，相互间差异不大，可以先选择其中的一个线性方程组作为种子系统预先求解，存储在求解过程中生成的子空间信息，在求解其余线性方程组时，将初始残量和搜索方向在此子空间上进行投影以加快算法的收敛速度.当多线性方程组的右端项靠近，即右端项向量间的夹角小时，算法有更好的收敛效果.由于（9）的右端项向量相互正交.设第k个线性方程组被选为种子系统，为改善右端项的靠近程度，构造一个新的多线性方程组

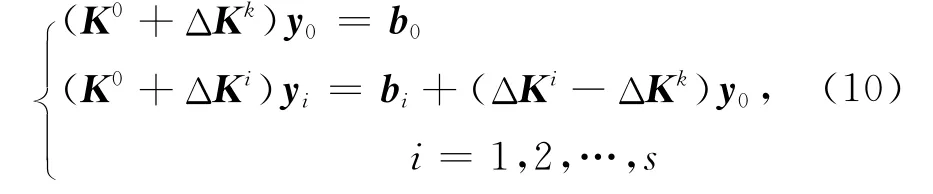
其中b0= （1，1，…，1）T是一个分量全为1的向量，bi= （1，1，…，1，0，1，…，1）T是一个对应点电源位置的分量为0，其余分量全为1的向量，方程（10）和（9）有如下关系：

（10）式的右端项之间满足

其中n是系数矩阵的维数，ei，ui分别为原多线性方程组（9）的右端项和未知项向量.由于（ΔAi-ΔAk）的范数很小，式（12）表明越大的n意味着新的多线性方程组的右端项越靠近，因此也应该有更好的收敛性.算法的具体实现见参考文献[19］.

3 反演问题

3.1 目标函数

井中激电的主要反演参数为电阻率和极化率，本文利用正则化原理和Gauss-Newton法反演.设m= （m1，m2，…，mM）T为模型参数向量，d= （d1，d2，…，dN）T为数据参数向量，数据误差为ε1，ε2，…，εN.取m=logσ，d=logρs，这里的σ（=1／ρ），ρs分别代表电导率和视电阻率，ρ为电阻率.给定目标函数为

其中λ为正则化因子，d（m）表示给定模型参数由正演计算得到的数据，dobs表示实际测量数据，D=diag（1／εi）为数据加权矩阵，W 为模型光滑性约束矩阵，mref是根据先验信息给出的参考模型.

利用Gauss-Newton法求目标函数的极小值，每步迭代更新如下：

其中α为线性搜索步长，Δmk为模型修正量.通过求解下面的线性方程组得到

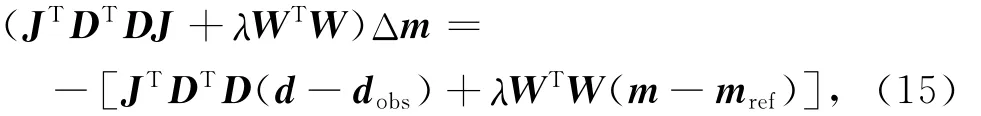
其中J=∂d／∂m，是Jacobian矩阵.方程（15）中光滑性约束W控制了模型单元在空间中的平稳变化程度，一般取为模型的离散差分算子.若对模型做一阶正则化约束，即最平模型估计，W 取为梯度算子.在三维情况下，需要在三个坐标方向上考虑，取

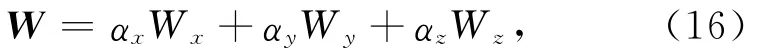
其中αx，αy，αz为三个坐标方向上的加权，用于控制在不同方向上的光滑程度，需要根据先验信息进行选择，如令αx取较大值时意味着解在x方向变化更平缓.

3.2 网格剖分

非结构化网格的生成过程比较复杂，TetGen是一款免费开源的四面体网格生成工具，可以方便地定义分区网格剖分和设置网格控制节点，本文中利用TetGen来生成非结构化网格.有限元正演的精度与网格剖分精细程度密切相关.为保证正演结果的精度，正演计算的网格需要剖分的足够精细；反演网格定义了模型参数的数目和区域的电性划分，若剖分过细，会造成测量数据个数和模型参数个数的比例更小，增大了反演过程的不适定性，并且增大了计算量.我们对反演网格进行较粗的剖分，采用结构化三棱柱单元或非结构化四面体单元.在每一个反演网格单元内进行加细剖分得到若干个正演网格单元，由同一个反演单元剖分得到的正演网格单元具有相同的模型参数属性.正反演采用不同的网格系统，需要处理的一个重要问题是正演和反演过程中的网格节点数据传递.由反演网格加密得到正演网格过程中，原反演网格的节点进行保留并保持编号不变，新增加的节点编号总是排在后面，这样的编号方式使正反演网格之间的数据传递不需要复杂的处理进行对应.

3.3 Jacobian矩阵计算

利用Krylov子空间法求解方程组（15），只需要计算Jacobian矩阵向量积，不必要直接计算和存储Jacobian矩阵，称为Jacobian-free Krylov方法[20-22］.利用求导的链式法则，对有限元方程（4）或（8）两边求导

于是

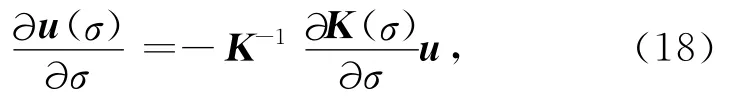
记

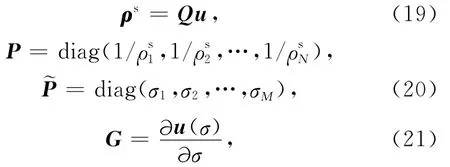
有

对任一向量

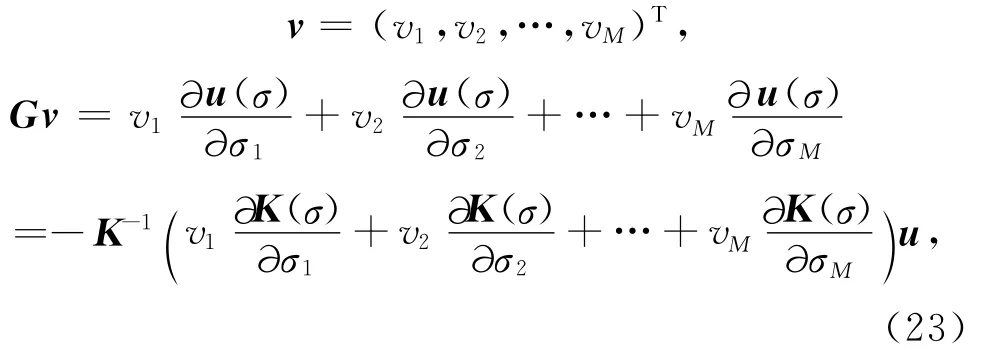
设ei表示第i个分量为1，其余分量为0的单位向量，由于刚度矩阵是电导率向量参数的线性算子，有

于是

对任意向量

其中z=K-1v.对于Jacobian矩阵转置与向量乘积，有

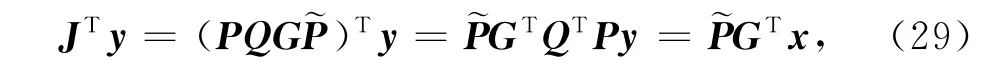
其中x=QTPy.实际计算GTv时利用一次单元刚度矩阵生成过程便可得到它的所有分量，只需要在每个有限单元上进行积分时设置电导率为1，在计算的同时乘以相应的ziuj，并只对属于同一反演单元的正演单元刚度矩阵进行累加.

（26），（28）和（29）式利用刚度矩阵表示，给出了Jacobian矩阵及其转置与向量的乘积的更为方便的计算方法，避免了显式地求取和存储刚度矩阵对电导率的导数.由于采用了精确的单元积分公式，而不采用数值积分，在计算Jv，JTv时做一次单元积分所花费的计算时间非常少.程序在Intel®CoreTM2 Duo CPU，2.66GHz，3.00GB内存，Windows XP下运行，对506262个四面体单元做一次单元积分生成总刚度矩阵所用CPU时间为0.75s.

在多个点源的情况下，设nsrc为点源个数，可以对每个源分别计算然后进行集成或累加，得到Jx，JTx.设Ji为第i个点源对应的Jacobian矩阵，则可将向量x进行相应的分解x= （x1，x2，…，xnsrc）T，有

3.4 反演算法

记

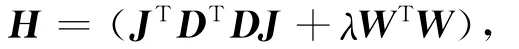
模型修正量方程（15）可写为

Dembo等指出，对方程组（33）只需要近似求解[23］.借鉴不精确Newton法的思想，我们采用不精确的PCG算法求解方程组（33）：设置较低的PCG迭代收敛准则和迭代次数限制；在计算矩阵向量积Hv时，设置较低的正演计算精度.

式（14）中线性搜索步长α应满足 Wolfe准则[21］，对不等式

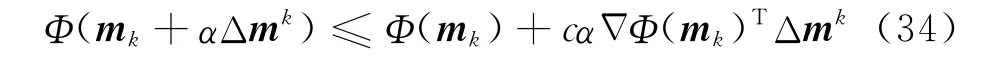
进行估计，若不等式不满足，则令

再进行估计判断.其中c为某一常数，一般取一个较小的数，如取为10-4，ρ∈（0，1）为某一常数，在本文的数值算例中我们取ρ=0.5.

正则化因子λ提供了最佳数据拟合和最合理解的折衷，对问题解的性态起着关键的作用.在测量数据的噪声水平参数δ可获取或能近似估计的情况下，偏差原理是一种广为采用的正则化参数选取策略.其基本思想是好的正则解应能使残量范数同数据噪声水平相符.记测量数据为dobs，设 ‖dtrue-dobs‖ ≤δ，则合适的解应满足

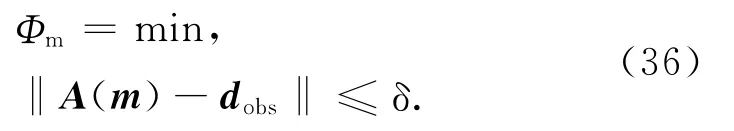
整个反演步骤如下：

（1）读入最大迭代次数限制、迭代停止准则等反演参数，读入初始模型，选择较大的值作为初始正则化因子；

（2）利用不精确PCG算法求解模型修正量Δmk；

（3）计算搜索步长α；

（4）更新模型参数mk+1=mk+αΔmk；

（5）估计残量，根据最大迭代次数限制和迭代收敛准则判断，若满足继续第6步，否则转到步骤2；

（6）根据偏差原理，判断不等式‖A（m）-dobs‖≤δ是否成立，若不成立，则减小正则化因子λ，转到步骤2；

（7）反演求解结束，输出结果.

3.5 极化率反演

极化率的反演我们采用算子线性近似方法[2，24］

在电阻率反演的基础上，加入光滑约束和先验信息，求解如下的目标函数极小问题：

利用PCG对（39）式求解，便得到相应的极化率参数.其中数据加权D及光滑性限制W和视电阻率反演的选择方式相同，λ的选择应满足偏差原理.

4 数值实验

4.1 算例1

见图2，背景电阻率为ρ=200Ωm，其中有一个低阻异常体，电阻率为ρ1=50Ωm，大小为30m×30m×20m，位于X：[-40m，-10m］，Y：[-40m，-10m］，Z：[50m，70m］处；一个高阻异常体，电阻率为ρ2=500Ωm，大小为30m×30m×20m，位于X：[10m，40m］，Y：[10m，40m］，Z：[30m，50m］处.

设分别在井中不同深度A0（z=0m），A1（z=20m），A2（z=50m），A3（z=70m）处固定A 极供电，在地面11条测线上逐点移动M极，在121个数据点上进行测量，得到484个视电阻率数.计算区域选为60m×60m×60m，将计算区域离散成12×12×12×2共3456个三棱柱体反演单元，2197个节点，在反演剖分的基础上进行正演网格剖分，得到234204个正演单元，40181个正演节点.

给定初始模型m0和先验模型mref为ρ=200Ωm的均匀模型，数据相对拟合差定义为

设置停止准则为R＜1×10-4，迭代8次达到收敛要求，所花CPU时间为187.79s，迭代收敛曲线见图3.

图4是Y=-53m，Y=-33m，Y=-16m，Y=16m，Y=33m，Y=53m处的电阻率反演切片图.从图上可以明显看出异常体的存在，异常位置反映基本准确.由于反演过程中对模型加入光滑性约束，反演出的异常体电阻率值与真实电阻率值有所偏差.

4.2 算例2

计算区域和网格剖分及模型大小设置同算例1.低阻体的电阻率为ρ1=50Ωm，极化率η1=5%，高阻体的电阻率为ρ2=500Ωm，极化率η2=10%，背景电阻率为ρ=200Ωm，极化率为η=1%.

进行井-井观测.在中间钻孔（X=0，Y=0）中不同深度A0（z=0m），A1（z=20m），A2（z=50m），A3（z=70m）处固定A极供电，在其它8个钻孔中共88个数据点上进行测量，8个测量钻孔的井口位置分别为：（X=-50m，Y=-50m）；（X=-50m，Y=50m）；（X=50m，Y=-50m）；（X=50m，Y=50m）；（X=0m，Y=30m）；（X=0m，Y=-30m）；（X=-30m，Y=0m）；（X=30m，Y=0m）.得到352个视电阻率和视极化率数据.

给定初始模型m0和先验模型mref为ρ=200Ωm的均匀模型，设置停止准则为R＜1×10-5，共迭代14次达到收敛要求.在电阻率反演基础上进行极化率反演，得到XOZ面的电阻率和极化率反演切片见图5，图6.从图上可以看到采用井-井方式，电阻率和极化率的反演效果都比较理想，异常体的形态和位置反映准确.

5 结 论

随着矿产资源的供需矛盾加剧，人们急需寻找第二找矿空间.井中激发极化法是深部金属矿勘探中的一种常用方法.本文系统研究了井中激发极化法的正反演技术，在电阻率法正反演的基础上实现激发极化数据的正反演.正演采用有限元方法，在正演基础上实现了井中激电的正则化反演.文中对网格剖分方式、高效的正反演算法、极化率的反演和方程组求解技术等方面进行了讨论.正演计算中采用了适合测井模型的剖分方式，可以处理地形、斜井和考虑井眼影响的模拟问题.对有限元方程进行右端项校正使算法在保证计算精度的前提下有效地减少了模拟区域的网格剖分数.改进的多线性方程组求解技术提高了正演的计算效率.反演采用Jacobianfree Krylov子空间技术，不需要计算和存储Jacobian矩阵，进一步推导了更为简便的Jacobian矩阵向量积的计算方法，避免了刚度矩阵对电导率求导的显式计算和存储.反演的迭代求解过程中，采用近似求解的思想减少了迭代次数和计算时间.在上述分析的基础上开发了正反演算法程序，数值算例验证了算法程序的效率和可靠性.

（References）

[1]Seigel H O.Mathematical formulation and type curves for induced polarization.Geophysics，1959，24（3）：547-565.

[2]Oldenburg D W，Li Y.Inversion of induced polarization data.Geophysics，1994，59（9）：1327-1341.

[3]Coggon J H.Electromagnetic and electrical modeling by the finite element method.Geophysics，1971，36（1）：132-155.

[4]Li Y G，Spitzer K.Three-dimensional DC resistivity forward modelling using finite elements in comparison with finitedifference solutions.Geophys.J.Int.，2002，151（3）：924-934.

[5]Sasaki Y.3-D resistivity inversion using the finite-element method.Geophysics，1994，59（12）：1839-1848.

[6]Pain C C，Herwanger J V，Worthington M H，et al.Effective multidimensional resistivity inversion using finiteelement techniques.Geophys.J.Int.，2002，151（3）：710-728.

[7]阮百尧，熊彬.电导率连续变化的三维电阻率测深有限元模拟.地球物理学报，2002，45（1）：131-138.Ruan B Y，Xiong B.A finite element modeling of threedimensional resistivity sounding with continuous conductivity.Chinese J.Geophys.（in Chinese），2002，45（1）：131-138.

[8]Lowry T，Allen M B，Shive P N.Singularity removal：a refinement of resistivity modeling techniques.Geophysics，1989，54（6）：766-774.

[9]Zhao S K，Yedlin M J.Some refinements on the finitedifference method for 3-D DC resistivity modeling.Geophysics，1996，61（5）：1301-1307.

[10]Pidlisecky A，Haber E，Knight R.RESINVM3D：A 3D resistivity inversion package.Geophysics，2007，72（2）：H1-H10.

[11]Spitzer K.A 3-D finite-difference algorithm for DC resistivity modelling using conjugate gradient methods.Geophys.J.Int.，1995，123（3）：903-914.

[12]吴小平，汪彤彤.利用共轭梯度算法的电阻率三维有限元正演.地球物理学报，2003，46（3）：428-432.Wu X P，Wang T T.A 3-D finite-element resistivity forward modeling using conjugate gradient algorithm.Chinese J.Geophys.（in Chinese），2003，46（3）：428-432.

[13]Loke M H，Chambers J E，Ogilvy R D.Inversion of 2D spectral induced polarization imaging data.Geophysical Prospecting，2006，54（3）：287-301.

[14]吴小平，徐果明.利用共轭梯度法的电阻率三维反演研究.地球物理学报，2000，43（3）：420-427.Wu X P，Xu G M.Study on 3-D resistivity reversion using conjugate gradient method.Chinese J.Geophys.（in Chinese），2000，43（3）：420-427.

[15]Rücker C， Günther T， Spitzer K.Three-dimensional modelling and inversion of DC resistivity data incorporating topography-I.modelling.Geophys.J.Int.，2006，166（2）：495-505.

[16]Günther T， Rücker C， Spitzer K.Three-dimensional modeling and inversion of DC resistivity data incorporating topography-II.inversion.Geophys.J.Int.，2006，166：506-517.

[17]徐世浙.地球物理中的有限单元法.北京：科学出版社，1994：178-188.Xu S Z.The Finite Element Method in Geophysics（in Chinese）.Beijing：Science Press，1994：178-188.

[18]任政勇，汤井田.基于局部加密非结构化网格的三维电阻率法有限元数值模拟.地球物理学报，2009，52（10）：2627-2634.Ren Z Y，Tang J T.Finite element modeling of 3-D DC resistivity using locally refined unstructured meshes.Chinese J.Geophys.（in Chinese），2009，52（10）：2627-2634.

[19]Li C W，Xiong B，Qiang J K，et al.Multiple linear system techniques for 3Dfinite element method modeling of direct current resistivity.Journal of Central South University，2012，19（2）：424-432.

[20]Knoll D A， Keyes D E.Jacobian-free Newton-Krylov methods：a survey of approaches and applications.Journal of Computational Physics，2004，193（2）：357-397.

[21]Nocedal J，Wright S J.Numerical Optimization.New York：Springer，2006.

[22]吴小平，徐果明.电阻率三维反演中偏导数矩阵的求取和分析.石油地球物理勘探，1999，34（4）：363-372.Wu X P，Xu G M.Derivation and analysis of partial derivative matrix in resistivity 3-D inversion.Oil Geophysical Prospecting （in Chinese），1999，34（4）：363-372.

[23]Dembo R S，Eisenstat S C，Steihaug T.Inexact Newton methods.SIAM J.Numer.Anal.，1982，19（2）：400-408.

[24]阮百尧，村上裕，徐世浙.激发极化数据的最小二乘二维反演方法.地球科学，1999，24（6）：619-624.Ruan B Y，Yutaka M，Xu S Z.Least square 2-D inversion method for induced polarization data.Earth Science（in Chinese），1999，24（6）：619-624.