可控源音频大地电磁三维共轭梯度反演研究

林昌洪，谭捍东，舒 晴，佟 拓，谭嘉言

1 中国地质大学（北京）地球物理与信息技术学院，北京 100083

2 中国地质大学地下信息探测技术与仪器教育部重点实验室，北京 100083

3 中国国土资源航空物探遥感中心，北京 100083

1 引 言

可控源音频大地电磁法（CSAMT）是在音频大地电磁法（AMT）基础上发展起来的一种人工源频率域测深方法，在勘探石油、天然气、地热、金属矿产、以及水文和环境工程中发挥了重要的作用[1-2］.

然而，与大地电磁法相比，可控源音频大地电磁资料反演技术的发展相对缓慢.其主要原因是源的问题，可控源音频大地电磁采用人工可控信号源，需要求解有源电磁波波动方程，因此处理方法相对复杂.目前可控源音频大地电磁实测资料的反演处理主要采用一维反演技术和对“被视做远区的资料”采用二维大地电磁反演技术.要想获得“远区资料”，需要收发距足够大使数据观测区满足远区场条件.而人工源方法，场源与接收点之间的距离越大，所接收到的电磁场信号的信噪比越低，加上测区的一些外在噪音，很难采集到高质量的可控源音频大地电磁资料.另外，地下介质的电阻率通常是未知的.因此，难以确定满足远区条件的收发距大小，也很难保证所采集到资料是“远区资料”，尤其是低频段资料.对这种数据采用大地电磁二维反演技术进行处理，容易得到错误的地质解释.因而，有些文献提出了对“近区资料”和“过渡区资料”进行校正的方法[3-4］，使得“近区和过渡区资料”满足平面波大地电磁数据的特征.但进行校正通常需要事先假设地电结构，如果假设的地电构造和实际情况相差较大，则容易得到错误的校正结果，并且对数据进行校正的过程中人为的影响因素较大.还有一些文献资料采用对视电阻率的重新定义来达到不做近场校正的目的[5-7］，但还未投入广泛应用.

为了解决这个问题，可以开发对可控源音频大地电磁数据进行直接反演的算法，有了直接反演算法，则在实际工作中不需要采集“远区资料”，可以减小收发距，增加信噪比，获得高质量的可控源音频大地电磁资料，并得出较可靠的地质解释.Routh等[1］在1999年提出了可控源音频大地电磁全资料一维水平层状介质的反演.王若等[8］在2007年采用网格参数法和剥层法实现了一维全资料可控源音频大地电磁反演.2008年，朱威等[9］用阻尼最小二乘法完成了可控源音频大地电磁一维全区反演.李帝铨等[10］在2008年基于遗传算法实现了可控源音频大地电磁一维最小构造反演.何梅兴等[11］在2008年实现了可控源音频大地电磁一维occam反演.汤井田等[12］在2011年采用了差商法实现可控源音频大地电磁一维最小构造反演.1999年，Lu等[2］采用快速松弛算法实现了可控源音频大地电磁三维源二维地质结构的反演方法.2006年，底青云等[13］也实现了可控源音频大地电磁三维源二维地质结构的快速松弛反演.2010年，雷达[14］采用occam反演方法实现了起伏地形下可控源音频大地电磁数据的二维反演.

然而，实际的地下地质情况比较复杂，地下电阻率结构可能是三维分布的，若对这样的实测资料进行一维或二维反演解释，很可能得到不可靠的地电模型[15-18］.为了充分发挥可控源音频大地电磁法的作用，提高可控源音频大地电磁在石油、矿产等领域的应用效果，应考虑开发可控源音频大地电磁数据三维反演算法.在对可控源音频大地电磁理论和共轭梯度算法深入分析的基础上，正演采用交错采样有限差分法[19-20］，反演采用共轭梯度法[21-28］，我们实现了可控源音频大地电磁资料三维共轭梯度反演算法.文中，首先讨论计算可控源音频大地电磁响应的三维正演问题，其次介绍可控源音频大地电磁三维共轭梯度反演方法理论，包括目标函数、反演流程和“拟正演”问题的计算，最后给出理论模型合成数据的三维反演结果.

2 三维正演

人工源条件下，场源附近电磁场总场的变化梯度大，直接数值模拟总场困难.我们采用把电磁场的总场分解成一次场（背景场）和二次场的叠加策略，分别计算出一次场和二次场，再合成总场[29］.如果电阻率、电场总场、磁场总场分别记为ρ、E（ρ）、H（ρ），背景电阻率（可为均匀半空间或层状介质）、一次 电 场、一次磁场总场分别记为ρb、E1（ρb）、H1（ρb），那么剩余电阻率 Δρ=ρ-ρb，二次电场E2（Δρ）=E（ρ）-E1（ρb），二 次 磁 场 H2（Δρ）=H（ρ）-H1（ρb）.

对于一次电场E1和一次磁场H1的计算，可从电磁场的麦克斯韦方程出发，结合势函数和电磁场理论，推导出水平层状介质在有限长度电偶源激发条件下，全空间节点处的电场和磁场的表达式，然后采用汉克尔变换方法实现可控源音频大地电磁全空间电场和磁场值的计算，为三维正演提供可靠的一次场值.

2.1 有限差分法求取二次电磁场

对于二次磁场H2，采用交错采样有限差分方法求解.将电阻率和电磁场总场满足的麦克斯韦方程：

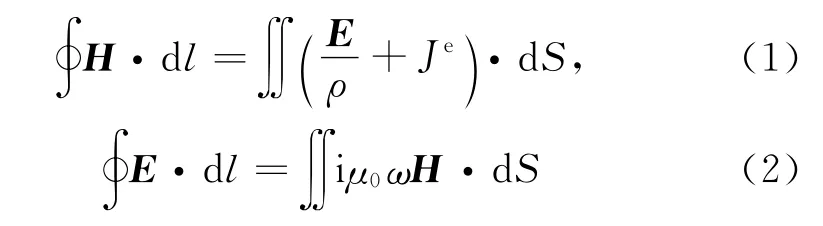
减去背景电阻率和一次电磁场满足的麦克斯韦方程：

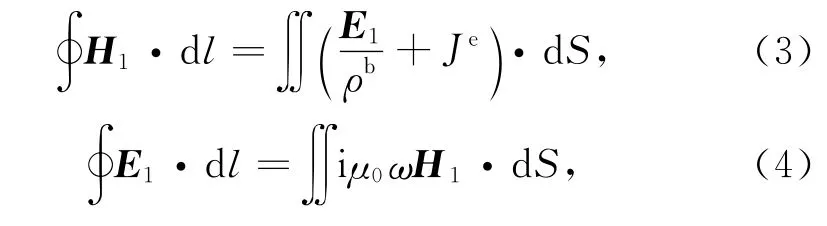
可得剩余电阻率和二次电磁场所满足的麦克斯韦方程：

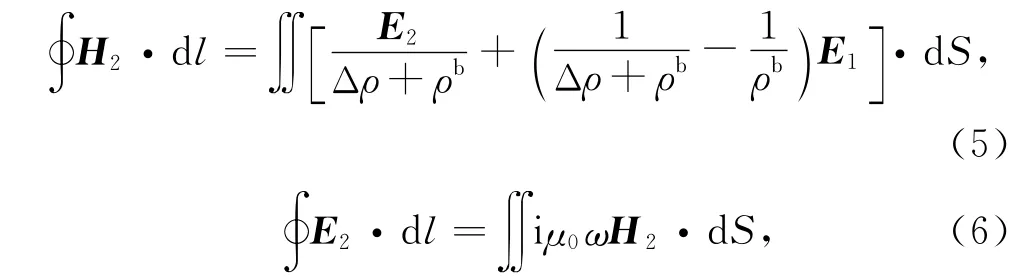
其中，ω表示角频率，μ0表示真空磁导率，Je表示源电流密度.

在笛卡儿右手坐标系中，用交错采样剖分网格[19］在研究区域内对剩余电阻率和二次场满足的麦克斯韦积分方程（5）和（6）进行离散化，可获得关于地下各网格单元采样点处二次磁场的正演方程：KH2=s， （7）其中，K为对称的大型稀疏系数矩阵；H2为待求解各网格单元采样点处的二次磁场三分量组成的列向量；s为与一次场及边界场值有关的列向量.求解该线性方程组从而获得二次磁场值列向量H2.

在求解二次磁场时，采取研究区域的空中顶边界、地下底边界和四个侧边界处的二次场值为零的方法处理边界条件.

求出二次磁场值列向量H2后，地表某观测点j处的二次磁场值H2j可以用磁场值列向量H2来表示：

这里H2j表示地表第j个观测点处模型块中心点的二次磁场值，它与H2之间通过内插向量hgTj转化.对于H2j的三个方向x、y、z分量，方程（8）分别对应为：

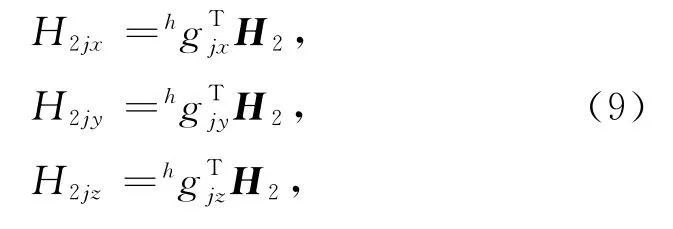
根据二次电场与二次磁场之间的差分关系式

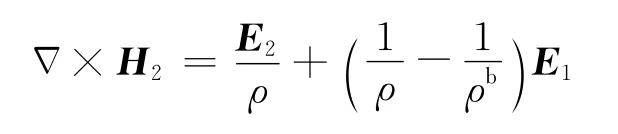
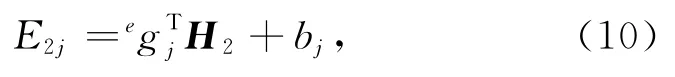
以及插值关系，在地表某观测点j处的二次电场值E2j也可以用磁场值列向量H2来表示：这里，E2j表示的是地表第j个观测点处模型块中心点的二次电场值，它和H2之间通过内插向量egTj转化，bj表示与背景电阻率以及一次场值相关的量.对于E2j的两个水平方向x、y分量，方程（10）分别对应

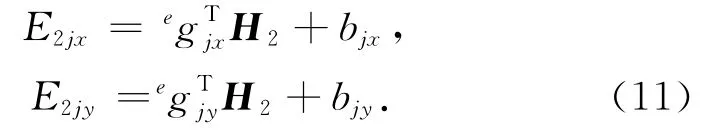
2.2 三维正演结果的检验

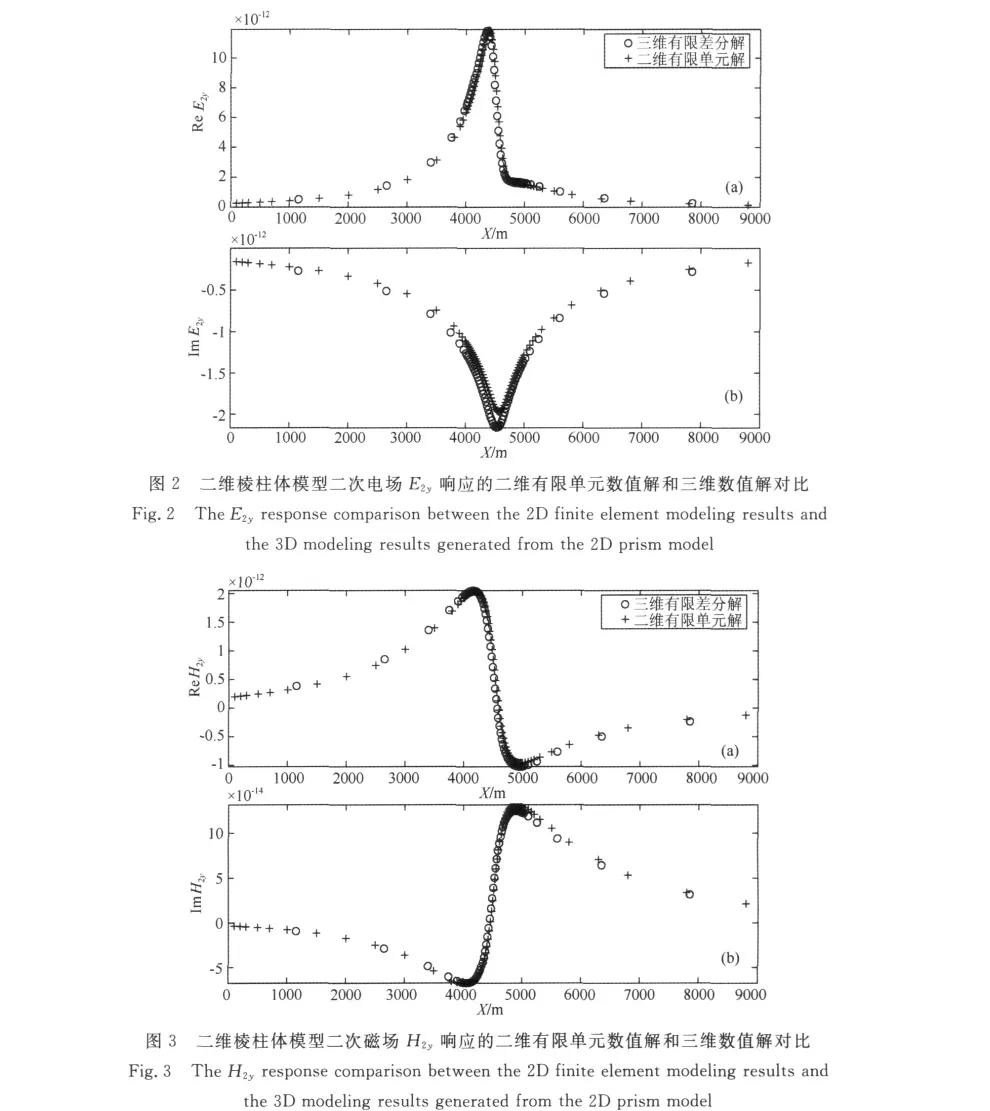
为了检验三维正演算法的正确性，我们设计了一个二维低阻棱柱体地电模型.如图1所示，大小为200m×100m，顶面埋深100m，走向为Y方向，电阻率为10Ωm的二维棱柱体埋藏于100Ωm均匀半空间.棱柱体中心在X方向离坐标原点的距离为4500m.电流为1A，方向为Y方向，长度为1m的电偶源位于地表（y=100m，x=0m，z=0m）.

用三维正演算法计算出该棱柱体在地表处的二次电磁场响应，再用二维有限单元法对该棱柱体进行数值模拟，得到二次电磁场响应.图2和图3对比了频率1Hz时，y=-100m测线处两种数值模拟计算结果得到的二次电场E2y和二次磁场H2y响应.图2和图3中，上图显示实部，下图显示虚部.由图可见，两种计算结果除了在E2y的虚部的峰值附近存在略微的差别外，其余结果都拟合得非常好.该结果表明三维正演算法的计算结果是准确可靠的.

2.3 三维视电阻率和相位响应

由于在反演中使用视电阻率和相位数据，在计算完一次电磁场和二次电磁场再合成电磁场总场后，还需要通过地表电磁场总场计算三维地电模型的视电阻率和相位响应.参考卡尼亚视电阻率的定义[1-2］，可以得到由地表总电场和总磁场计算地表视电阻率和相位的表达式：

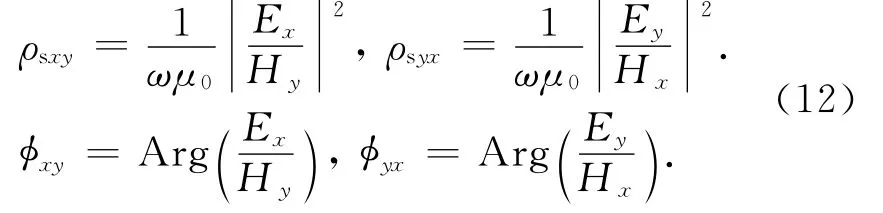
其中，Ex和Ey分别表示地表x和y方向总电场，Hx和Hy分别表示地表x和y方向总磁场.

3 三维反演

可控源音频大地电磁数据的三维反演是一项复杂的工作，由于实测数据量大，参加反演的模型参数多，对计算机硬件资源的要求高，需要花费大量的计算时间.如何快速而又可靠地得出三维反演的结果是可控源音频大地电磁三维反演问题向实用化方向发展的关键.针对这个问题，我们采用共轭梯度反演方法求解可控源音频大地电磁资料的三维反演问题.

3.1 目标函数

可控源音频大地电磁三维共轭梯度反演算法的目标函数定义为：

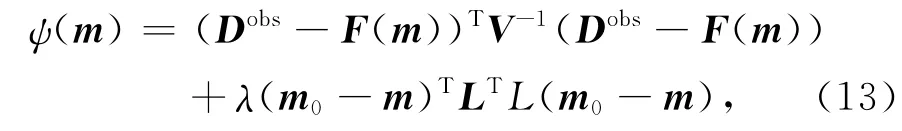
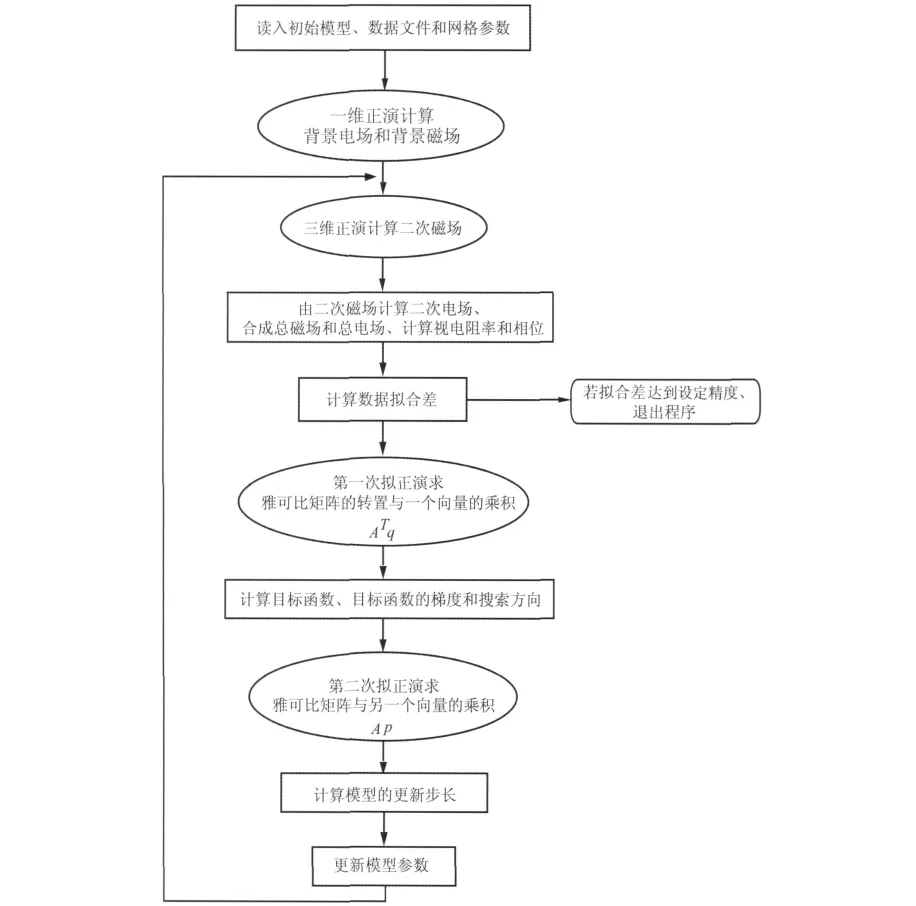
图4 可控源音频大地电磁三维共轭梯度反演算法流程图Fig.4 The flowchart of CSAMT 3Dconjugate gradient inversion

其中，Dobs表示观测视电阻率或相位数据；F（m）为求取可控源音频大地电磁响应的正演函数；V为数据方差；λ为正则化参数；L为简单的二次差分拉普拉斯算子，m表示模型参数，m0为先验模型.目标函数的梯度相应可表示为：

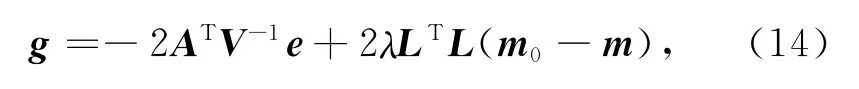
这里，A表示雅可比矩阵，数据拟合差向量：e=Dobs-F（m）.

3.2 反演流程

可控源音频大地电磁三维共轭梯度反演算法的大致流程（见图4）为：

（1）设置迭代次数i=0，输入反演的初始模型、反演数据和模型剖分参数等；

（2）一维正演，计算一次电场E1和一次磁场H1；

（3）三维正演，解正演方程KH2=s得到二次磁场H2；

（4）由二次磁场H2计算二次电场E2，根据一次电磁场E1、H1和二次电磁场E2、H2合成地表总电磁场，再由地表总电磁场计算视电阻率ρ和相位φ；

（5）计算数据拟合差eTV-1e，如果拟合差达到设定的精度，退出循环，结束程序，否则继续；

（6）通过“拟正演”问题计算ATV-1e；

（7）计算目标函数ψi，目标函数的梯度gi；

（8）通过hi=Cgi，βi=hTi（gi-gi-1）／hTi-1gi-1更新搜索方向pi=-hi+βipi-1；

（9）通过“拟正演”问题计算f=Api；

（10）计算模型的更新步长

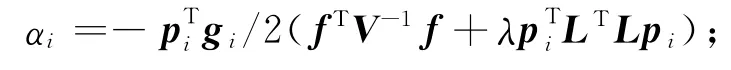
（11）更新模型参数mi=mi-1+αipi；

（12）i=i+1，回步骤（3）.

3.3 雅可比矩阵的计算-“拟正演”问题

从反演流程可以看出，反演中只要计算出ATq和Ap（其中，q=V-1e，p表示搜索方向），就可以得到每次模型迭代的修正量.可控源音频大地电磁三维共轭梯度反演算法不通过逐个计算雅可比矩阵A的每个元素来求取ATq和Ap，而是通过解“拟正演”问题来直接计算出ATq和Ap的值，下面我们介绍如何通过解“拟正演”问题来直接计算出ATq和Ap的值.

由于背景电阻率ρb是固定值，在反演中我们选取剩余电阻率Δρ为反演模型参数，正演方程（7）两端同时对模型参数Δρ求偏导数，则有：

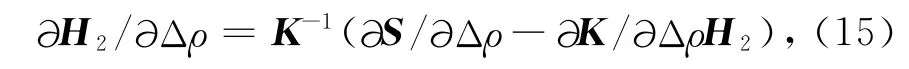
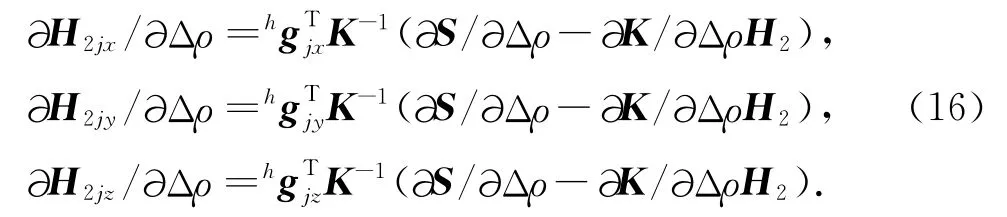
将公式（11）代入方程（15）可得：

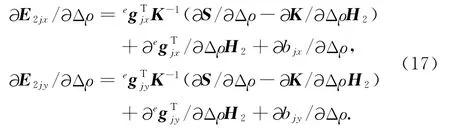
与三维正演相对应，反演过程中的电磁场总场对模型参数的偏导数也可分解成一次场和二次场来求对模型参数的偏导数：

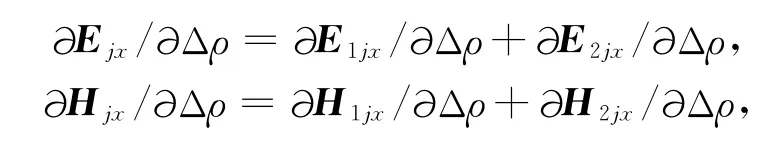
其中，一次场对剩余电阻率Δρ的偏导数为零（一次场与剩余电阻率Δρ无关）：

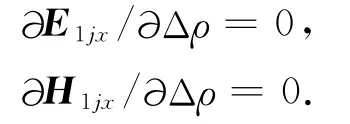
则总场对模型参数的偏导数只剩下二次磁场对模型参数的偏导数，因此，公式（16）和公式（17）可以进一步改写为：

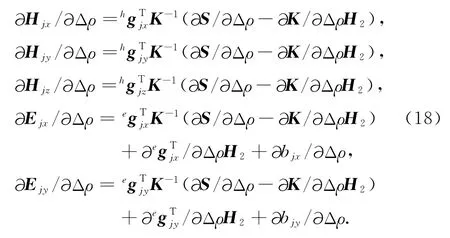
把方程（12）中视电阻率和相位构成的复视电阻率对第k个模型参数Δρ求偏导数，可得：

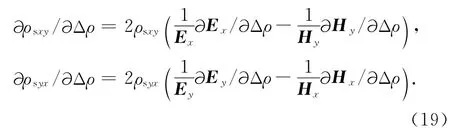
将方程（18）代入方程（19），则第k个模型参数Δρ的扰动所引起的第j个观测点处复视电阻率的改变量∂ρsxy／∂Δρ和∂ρsyx／∂Δρ可以写成如下形式：

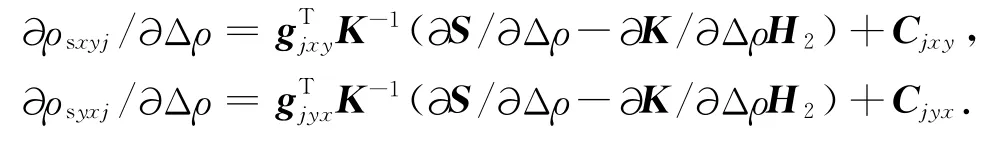
其中，

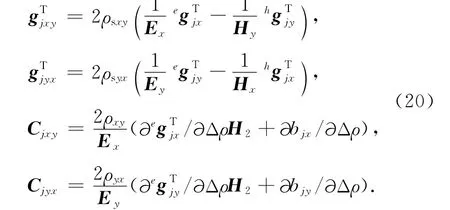
由于使用视电阻率和相位资料作为反演数据，那么雅可比矩阵A的元素是反演数据对Δρ求偏导数，也就是视电阻率或相位数据对Δρ求偏导数（∂ρsxy／∂Δρ和∂ρsyx／∂Δρ），即公式（20）中的模型参数Δρ的扰动所引起的观测点处复视电阻率的改变量.因此，ATV-1e可表示为：

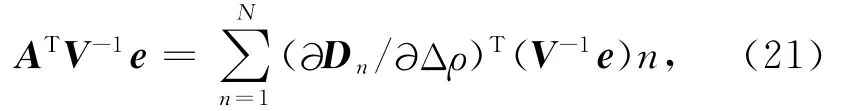
其中，n=1，2，…，N表示反演数据，N为视电阻率和相位数据的总个数：测点数×频率数×2.根据公式（20），并由K为对称阵可进一步整理得：

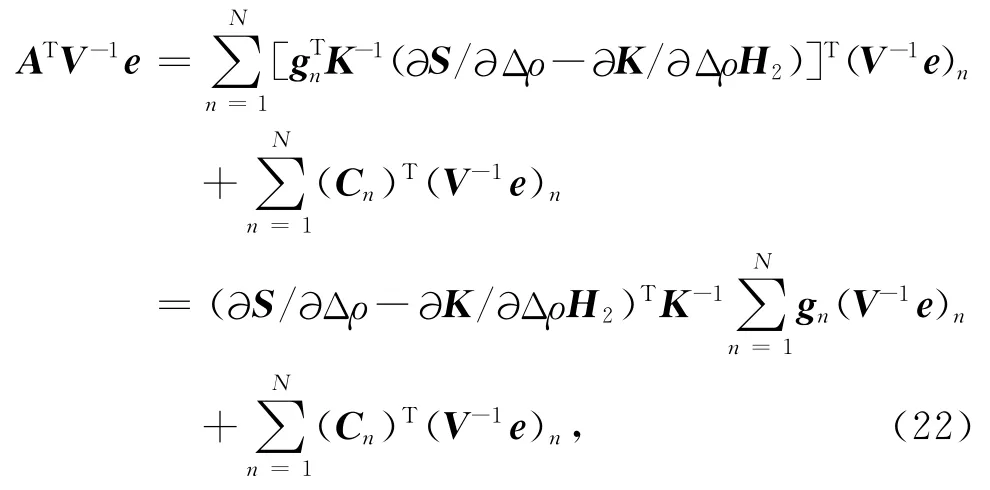
其中，gn、Cn由式（20）确定.例如：如果ρsxyj为第n个数据，那么令：

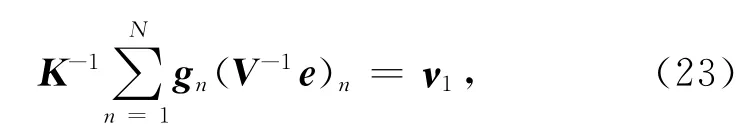
则：

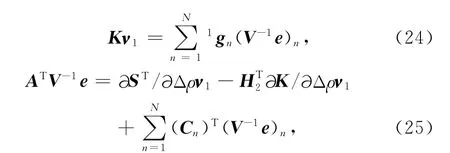
把ν1视为解向量，视为方程右端向量，式（24）是一个和式（7）类似的正演方程，我们称之为“拟正演”方程.通过解一次“拟正演”方程，可以得到v1.把v1代入式（25），可以直接计算出ATV-1e.

同理，对于Ap，经过推导可得：

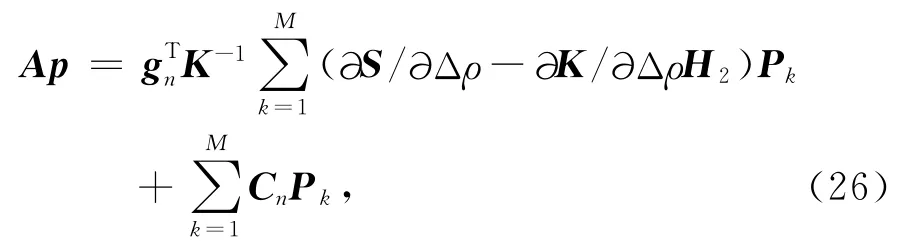
其中，k=1，2，…，M 表示模型参数.

令：

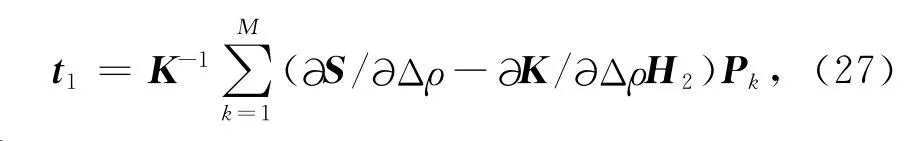
则有：

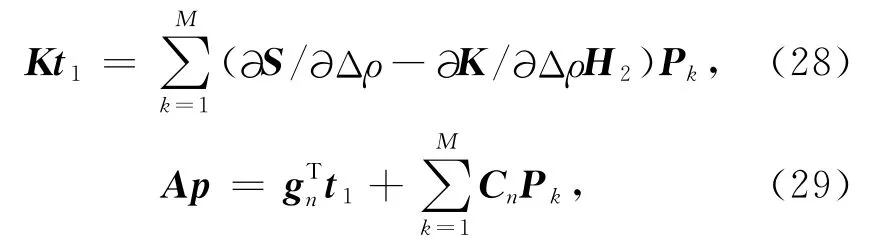
把t1视为解向量，视为方程右端向量，式（28）也是一个和式（7）类似的正演方程，我们称之为“拟正演”方程.通过解一次“拟正演”方程，可以得到t1.把t1代入式（29），可以计算出Ap.这样通过解一次“拟正演”问题，也可以直接得到Ap.

4 理论模型合成数据反演算例

基于上面的理论和公式，我们编程开发了可控源音频大地电磁三维共轭梯度反演程序.为了检验三维反演算法的有效性，我们设计了两个三维地电模型.

4.1 模型一

设计的低阻棱柱体模型如图5第一行所示.大小为200m×200m×100m，顶面埋深为100m，电阻率为10Ωm的低阻棱柱体埋藏于电阻率为100Ωm的均匀半空间.

取棱柱体中心在地表处的投影点为坐标原点，在x=0km，y=-7km，z=0km的地表处放置长度为100m的X方向水平电偶源.三维网格剖分为46×46×33（含10个空气层）.用可控源音频大地电磁三维共轭梯度反演程序的正演代码部分计算出单棱柱体模型在地表所有剖分网格单元中心点处产生的9个频率（4000、2000、1000、500、200、100、10Hz、1和0.1Hz）的视电阻率和相位数据.

初始模型为100Ωm均匀半空间，正则化因子λ=10-4，对地表900个测点处（测区范围X：-300～300m，Y：-300～300m）的9个频率视电阻率ρsxy和相位数据φxy中加入1%高斯随机误差后用可控源音频大地电磁三维共轭梯度反演程序在PC机上进行反演.PC机的配置（下同）为：Intel（R）core（TM）i7处理器，主频2.93GHz，内存4.0G.经过33次反演迭代，耗时22小时11分钟，数据的拟合方差从初始值12.06收敛到0.99迭代结束.反演的结果见图5的第二行，从图中可以看出三维反演结果基本与理论模型一致（图5的第一行）.

当场源位于x=0km，y=-7km，z=0km时，从场源相对测区的位置及所使用的频率分析，测区可近似看作远区.为了检验三维反演程序是否可用于对过渡区和近区数据进行三维反演，其他参数保持不变，把场源位置改为x=0km，y=-1km，z=0km和x=0km，y=-0.3km，z=0km 时，三维反演的结果见图5的第三行和第四行.从图中可以看出，除了当场源位于x=0km，y=-0.3km，z=0km时，三维反演得到的低阻体在Y方向稍微有些拉长（分析其原因可能与场源有关，低阻体拉长的位置正好位于场源位置附近的下方），其余结果都基本与理论模型相一致.

4.2 模型二

设计的低阻棱柱体和高阻棱柱体组合模型如图6第一行所示.大小为200m×200m×100m，顶面埋深为100m，电阻率分别为10Ωm和1000Ωm的两个棱柱体埋藏于电阻率为100Ωm的均匀半空间.

和模型一类似，在x=0km，y=-7km，z=0km的地表处放置长度为100m的X方向水平电偶源.三维网格剖分为66×46×33（含10个空气层）.初始模型为100Ωm均匀半空间，正则化因子λ=10-4，对地表1500个测点处（测区范围X：-500～500m，Y：-300～300m）的9个频率视电阻率ρsxy和相位数据φxy中加入1%高斯随机误差后用可控源音频大地电磁三维共轭梯度反演程序在PC机上进行反演.经过28次反演迭代，耗时35小时30分钟，数据的拟合方差从初始值10.28收敛到0.98迭代结束.反演的结果见图6的第二行.

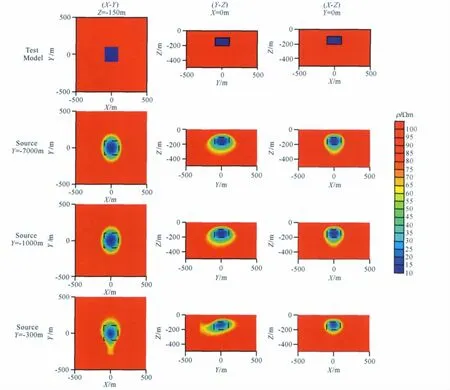
图5 模型一的三维反演结果图中第一行表示真实模型，第二行为场源位于x=0km，y=-7km，z=0km处时的三维反演结果，第三行为场源位于x=0km，y=-1km，z=0km处时的三维反演结果，第四行为场源位于x=0km，y=-0.3km，z=0km处时的三维反演结果.黑色虚线表示棱柱体的边界.第一列为深度150m处的水平截面图，第二列为X=0m处沿Y方向的垂直断面图，第三列为Y=0m处沿X方向的垂直断面图.Fig.5 The 3Dinversion results of model 1 The top row shows the test model.The second row shows the results from the 3Dinversion when the dipole source locates at the position（x=0km，y=-7km，z=0km）.The third row shows the results from the 3Dinversion when the dipole source locates at the position（x=0km，y=-1km，z=0km）.The fourth row shows the results from the 3Dinversion when the dipole source locates at the position（x=0km，y=-0.3km，z=0km）.The black dashed lines show the prism margins.The first column shows the horizontal slices at 150m depth，the second column shows the vertical slices at X=0malong the Yaxis，and the third column shows the vertical slices at Y=0m along the Xaxis.

5 结 论

正演采用交错采样有限差分数值模拟方法，反演采用正则化反演方案和共轭梯度反演思路，将反演中的雅可比矩阵计算问题转为求解两次“拟正演”问题，得到模型参数的更新步长，我们实现了可控源音频大地电磁三维共轭梯度反演算法.该反演算法可用于对有限长度电偶源激发下采集到的可控源音频大地电磁全区（近区、过渡区和远区）视电阻率和相位资料进行三维反演定量解释，获得地下三维模型的电阻率结构.理论模型合成数据的反演算例验证了所实现的可控源音频大地电磁三维共轭梯度反演算法的有效性和稳定性.

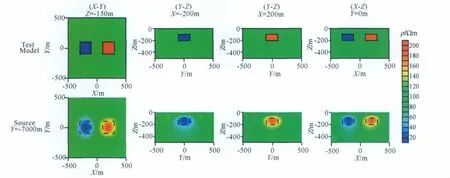
图6 模型二的三维反演结果图中第一行表示真实模型，第二行为三维反演结果.黑色虚线表示棱柱体的边界.第一列为深度150m处的水平截面图，第二列为X=-200m处沿Y方向的垂直断面图，第三列为X=200m处沿Y方向的垂直断面图，第四列为Y=0m处沿X方向的垂直断面图.Fig.6 The 3Dinversion results of model 2 The top row shows the test model.The second row shows the 3Dinversion results.The black dashed lines show the prism margins.The first column shows the horizontal slices at 150mdepth，the second column shows the vertical slices at X=-200malong the Yaxis，the third column shows the vertical slices at X=200malong the Yaxis，and the forth column shows the vertical slices at Y=0malong the Xaxis.

（References）

[1]Routh P S，Oldenburg D W.Inversion of controlled source audio-frequency magnetotellurics data for a horizontally layered earth.Geophysics，1999，64（6）：1689-1697.

[2]Lu X Y，Unsworth J M，Booker J.Rapid relaxation inversion of CSAMT data：Geophysical Journal International，1999，138（2）：381-392.

[3]Yamashita M，et al.CSAMT case histories with a multichannel CSAMT system and discussion of near-field data correction.Phoenix Geophys，Ltd，1985.

[4]罗延钟，周玉水，万乐.一种新的CSAMT资料近场校正方法.勘查地球物理勘查地球化学文集第20集.北京：地质出版社，1996.Luo Y Z，Zhou Y S，Wan L.A New Correction Method for CSAMT Near-field Data.The 20thCorpus of Exploration Geophysics and Geochemistry（in Chinese）.Beijing：Geology Press，1996.

[5]汤井田，何继善.水平电偶源频率测深中全区视电阻率定义的新方法.地球物理学报，1994，（4）：543-552.Tang J T，He J S.A new method of define the full-zone resistivity in horizontal electric dipole frequency soundings on a layered earth.Chinese J.Geophys.（in Chinese），2011，54（1）：245-256.

[6]苏发，何继善.组合波近区频域电磁测深研究.中国科学（E辑），1996 ，26（3）：240-246.Su F，He J S.Study on the combination wave electromagnetic sounding in frequency domain.Science in China （Series E）（in Chinese），1996，26（3）：240-246.

[7]汤井田，何继善.水平多层介质上水平电偶源频率电磁测深的阻抗实部等效电阻率.物探与化探，1994，18（2）：92-96.Tang J T，He J S.Impedance real part equivalent resistivity in frequency electromagnetic sounding of horizontal electric double source on horizontal multilayer media.Geophysical &Geochemical Exploration.（in Chinese），1994，18（2）：92-96.

[8]王若，王妙月.一维全资料CSAMT反演.石油地球物理勘探，2007，42（1）：107-114.Wang N，Wang M Y.Inversion of 1-D full CSAMT data.Oil Geophysical Prospecting （in Chinese），2007，42（1）：107-114.

[9]朱威，李桐林，尚通晓等.CSAMT一维全区反演对比研究.吉林大学学报（地球科学版），2008，38（增刊）：12-14.Zhu W，Li T L，Shang X T.Compared study of 1-D fullregion inversion of CSAMT.Journal of Jilin University（in Chinese），2008，38：12-14.

[10]李帝铨，王光杰，底青云等.基于遗传算法的CSAMT最小构造反演.地球物理学报，2008，51（4）：1234-1245.Li D Q，Wang G J，Di Q Y，et al.The application of Genetic Algorithm to CSAMT inversion for minimum structure.Chinese J.Geophys.（in Chinese），2008，51（4）：1234-1245.

[11]何梅兴，胡祥云，陈玉萍等.奥克姆一维反演的应用.工程地球物理学报，2008，5（4）：439-443.He M X，Hu X Y，Chen Y P，et al.Application of 1D Occam′s inversion to CSAMT.Chinese Journal of Engineering Geophysics.（in Chinese），2008，5（4）：439-443.

[12]汤井田，张林成，肖哓等.基于频点CSAMT一维最小构造反演.物探化探计算技术，2011，33（6）：577-581.Tang J T，Zhang L C，Xiao X，et al.One dimension CSAMT minimum structure inversion based on the frequency.Computing Techniques for Geophysical &Geochemical Exploration.（in Chinese），2011，33（6）：577-581.

[13]底青云，Martyn Unsworth，王妙月.2.5维有限元法CSAMT数值反演.石油地球物理勘探，2006，41（1）：100-106.Di Q Y，Unsworth M，Wang M Y.2.5-D finite-element CSAMT numerical inversion.Oil Geophysical Prospecting（in Chinese），2006，41（1）：100-106.

[14]雷达.起伏地形下CSAMT二维正反演研究与应用.地球物理学报，2010，53（4）：982-993.Lei D.Studies and applications of 2-D CSAMT modeling and inversion with a dipole source and topography.Chinese J.Geophys.（in Chinese），2010，53（4）：982-993.

[15]胡祖志，胡祥云，何展翔.三维大地电磁数据的二维反演解释.石油地球物理勘探，2005，40（3）：353-359.Hu Z Z，Hu X Y，He Z X.Using 2-D inversion for interpretation of 3-D MT data.Oil Geophysical Prospecting（in Chinese），2005，40（3）：353-359.

[16]Ledo J.2-D Versus 3-D Magnetotelluric Data Interpretation.Surveys in Geophysics，2005，26：511-543.

[17]林昌洪，谭捍东，佟拓.利用大地电磁三维反演方法获得二维剖面附近三维电阻率结构的可行性.地球物理学报，2011，54（1）：245-256.Lin C H，Tan H D，Tong T.The possibility of obtaining nearby 3Dresistivity structure from magnetotelluric 2D profile data using 3Dinversion.Chinese J.Geophys.（in Chinese），2011，54（1）：245-256.

[18]Lin C H，Tan H D，Shu Q，et al.Three-dimensional interpretation of sparse survey lines magnetotelluric data：synthetic examples.Applied Geophysics，2012，9（1）：9-18.

[19]谭捍东，余钦范，Booker John等.大地电磁法三维交错采样有限差分数值模拟.地球物理学报，2003，46（5）：705-711.Tan H D，Yu Q F，Booker J，et al.Magnetotelluric threedimensional modeling using the staggered-grid finite difference method.Chinese J.Geophys.（in Chinese），2003，46（5）：705-711.

[20]Lin C H，Tan H D，Tong T.Parallel rapid relaxation inversion of 3Dmagnetotelluric data.Applied Geophysics，2009，6（1）：77-83.

[21]Mackie R L，Madden T R.Three-dimensional magnetotelluric inversion using conjugate gradients.Geophys.J.Int.，1993，115：215-229.

[22]Newman G A， Alumbaugh D L.Three-dimensional magnetotelluric inversion using non-linear conjugate gradients.Geophys.J.Int.，2000，140：410-424.

[23]Rodi W， Mackie R L.Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion.Geophysics，2001，66：174-187.

[24]胡祖志，胡祥云，何展翔.大地电磁非线性共轭梯度拟三维反演.地球物理学报，2006，49（4）：1226-1234.Hu Z Z，Hu X Y，He Z X.Pseudo-three-dimensional magnetotelluric inversion using nonlinear conjugate gradients.Chinese J.Geophys.（in Chinese），2006，49（4）：1226-1234.

[25]Lin C H，Tan H D，Tong T.Three-dimensional conjugate gradient inversion of magnetotelluric sounding data.Applied Geophysics，2008，5（4）：314-321.

[26]Lin C H，Tan H D，Tong T.Three-dimensional conjugate gradient inversion of magnetotelluric impedance tensor data.Journal of Earth Science，2011，22（3）：386-395.

[27]林昌洪，谭捍东，佟拓.倾子资料三维共轭梯度反演研究.地球物理学报，2011，54（4）：1106-1113.Lin C H，Tan H D，Tong T.Three-dimensional conjugate gradient inversion of tipper data.Chinese J.Geophys.（in Chinese），2011，54（4）：1106-1113.

[28]Lin C H，Tan H D，Tong T.Three-dimensional conjugate gradient inversion of magnetotelluric full information data.Applied Geophysics，2011，8（1）：1-10.

[29]Unsworth J M，Bryan J T，Alan D C.Electromagnetic induction by a finite electric dipole source over a 2-D earth.Geophysics，1993，58（2）：198-214.