基于二阶导数的磁源边界与顶部深度快速反演
张恒磊,胡祥云,刘天佑
1 中国地质大学(武汉)地球物理与空间信息学院,武汉 430074
2 中国地质大学(武汉)构造与油气资源教育部重点实验室,武汉 430074
1 引 言
磁法勘探作为地球物理勘探的一个重要分支,其发展最早,理论成熟,广泛应用于油气与固体矿产勘探、环境与工程地球物理勘查、区域与深部构造研究等领域.对磁异常进行反演是地质-地球物理解释中的一项重要工作,通过它可以获取场源位置、埋深等参数,并与地质资料相结合,可以了解更加丰富、全面的地下地质信息,提高解释质量.
在磁异常反演[1]中,除了一些相对简单的经验切线法,大多需要经过反复的正反演计算,同时需要提供物性参数.为了约束反演的多解性,常常需要充分结合地质信息才能获得满意的结果,其过程费时费力.尤其在地质工作初期,物性参数缺乏、地质因素不甚明了,很难实现磁异常的有效反演.2007年,Salem等[2]在Tilt梯度分析场源边界的基础上,重新分析了Tilt梯度的含义,并通过理论推导,扩展了Tilt梯度的物理意义[3],即 Tilt_depth反演方法.研究指出,在简单理想模型数值实验中,Tilt_depth方法无需提供先验信息,即可以精确的反演出场源的上顶埋深,他们利用该方法对坦桑尼亚东南部的航磁异常进行分析,推断解释的基底构造与地质填图结果相吻合,证明了方法的简洁有效.2008年,Salem等[4]撰文讨论了基于磁异常梯度的解释方法,并把Tilt_depth方法应用于纳米比亚中北部的航磁异常处理中,得到了客观的解释结果;2009年,Lee等[5]讨论了Tilt_depth方法的应用前提,随后Lahti和Karinen于2010年撰文讨论了磁异常幅值大小对深度反演的影响并进一步分析了Tilt_depth方法的理论条件[6].2011年,Fairhead等[7]对Tilt方法的应用效果进行了讨论,并成功应用于沉积盆地的结构划分与深度反演.目前,Tilt_depth方法得到了广泛的应用[8-11];在国内研究领域,也有不少学者对Tilt_depth方法进行跟踪报道[12-15],体现了这种方法的优越性与广泛适用的特点.
本文指出了Tilt_depth方法存在的问题,在此基础上,推导了基于垂向二阶导数的磁异常非参数反演,以期得到更好的边界识别效果以及更精确的深度反演.同时,笔者讨论了本文方法的稳定计算问题,提出采用向上延拓的处理方法代替传统的低通滤波消除高频干扰,实现稳定计算.
2 方法原理
2.1 Tilt梯度与Tilt_depth
1994年,Miller和Singh首次给出了Tilt梯度的数学定义[2],并用于位场异常边界分析.它一定程度上克服了常规位场导数对深部异常、弱异常反应欠佳的弊端.Tilt梯度值对于场源的深度不敏感,计算结果不受场源埋深情况制约,因此它能够很好的探测出具有不同埋深的复杂场源体的边界.Tilt梯度的公式是根据二维解析信号发展而来的,它定义为位场异常的垂直导数与水平导数比值的反正切,表达式为:

式中,f表示位场异常,∂f/∂z指位场异常的垂向导数,其值在场源上方为正,在场源外侧为负,在场源边界位置附近其值为零;∂f/∂h指位场异常的水平导数,对于平面异常
2007年,Salem等用二度直立板状体垂直磁化时的磁异常公式,导出场源顶深与异常的两个一阶导数之比(垂向一阶导数与水平一阶导数)的关系式[3]:

式中x指空间坐标,z0指二度直立板状体的上顶深度.
分析可知,这个关系对二度直立板状体垂直磁化情形是精确的,其它情形都是近似的.对剖面数据,由两个一阶导数之比的反正切绘制剖面图,图上两点(-45°和45°)之间的水平距离为场源顶深z0的2倍,0°值点对应场源边界;对平面数据,由两个一阶导数之比的反正切绘制平面等值线图,由该图上两条等值线(-45°和45°)之间的距离的一半确定场源顶深,由0°等值线确定场源边界.
2.2 V2D_depth非参数反演
Salem等[2]基于垂向一阶导数的Tilt方法不利于区分叠加异常,同时它识别的异常边界与实际情况差别较大.本文把前人得到的一阶导数关系式推广至二阶形式,导出场源顶深与异常的两个二阶导数之比(垂向二阶导数与水平二阶导数)的关系式,即V2D_depth方法.
二度棱柱体模型产生的磁异常计算公式为[16]:ΔT(P)=


图1 二度模型导数计算坐标示意图Fig.1 Notation used to derive the magnetic anomaly due to a two-dimensional
其中,k表示磁化率,F表示地球磁场值的大小,c=1-cos2i·sin2A(A为测线磁方位角,i为地磁倾角),φ=2I-d-90,I表示有效磁化倾角 (tanI=tani/cos A),其它参数详见图1中说明.
1972年,Nabighian推导了(3)式的垂向梯度公式,如下:

对于垂直物性边界的地质体,d=90°,对于化极磁异常,I=90°,故有φ=0°.(4)式可以进一步表示为

进一步推导可得如下关系式:
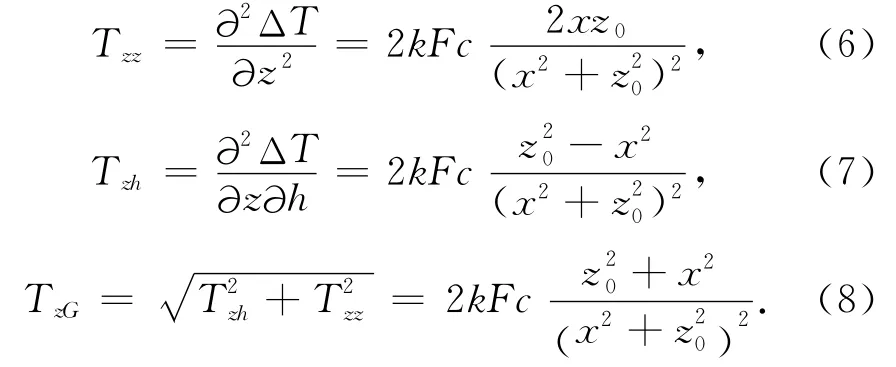
上述公式中Tzz表示ΔT磁异常的垂向二阶导数,Tzh表示ΔT磁异常的垂向一阶导数Tz的水平导数,对于平面磁异常,
根据式(6)和式(8)即可以得到如下比值关系:

由此可以确定基于垂向二阶导数的非参数反演算法,即
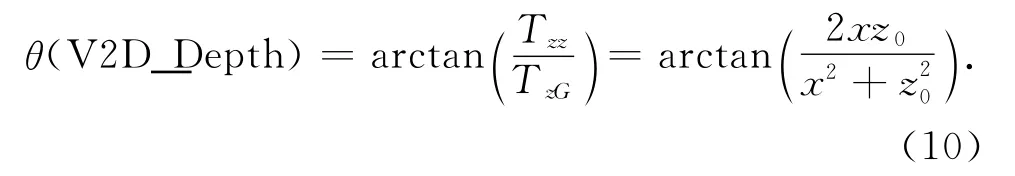
2.3 分析讨论与计算流程
在位场反演中,有一些方法利用了理论上场与场源特征参数之间的某种特殊关系,直接利用位场异常的特征点进行反演,即所谓的直接法,比如生产实践中常用的经验切线法等.与这些简单的方法相似,Tilt_depth方法与本文方法反演过程无需输入参数,笔者称这种无需先验信息即无需输入参数的反演方法为“非参数反演方法”.
分析Tilt_depth与本文方法,有以下几方面性质.
(1)Salem 等[3]指出 Tilt_depth方法容易受叠加异常干扰,±45°等值线间距在场源四周有疏有密并且差异很大,直接影响埋深参数的反演,限制了方法的使用.
(2)在文献[17-18]中,笔者利用类似“广义的水平二阶导数”类方法计算重磁源边界,并通过理论与实践证明了方法的有效性.联系位场拉普拉斯方程Txx+Tyy+Tzz=0,因此本文的公式(10)得到的边界与文献[17-18]有相似的分析结果,它比Tilt_depth方法分析的边界更接近真实情况.
(3)V2D_depth方法也是通过计算 V2D_Depth对应的两条等值线(特征等值线)之间的空间距离来反演深度.比如,x=±z0,x=±z0/2或者x=±z0/4两条等值线,分别对应±arctan(1)、±arctan(4/5)和±arctan(8/17)等值线,将它们之间的空间距离分别乘以0.5、1、2即可以得到反演的上顶深度.
(4)基于导数的计算方法对噪声干扰异常敏感,本文方法也不例外.本文中笔者建议采用向上延拓的方式避免高频干扰引起的计算振荡现象.
基于以上分析,本文算法的计算流程如下:
(1)将获得的磁异常进行化到地磁极计算;
(2)对化极磁异常向上延拓消除高频干扰——上延的高度视噪声水平灵活设定;
(3)计算异常的垂向二阶导数、垂向一阶导数的水平导数;
(4)按照公式(10)将上述导数进行比值计算,并取反正切,得到本文的θ(V2D_Depth)值;
(5)计算θ(V2D_Depth)特征等值线之间距,减去相应的延拓高度,得到地质体的上顶深度.
3 理论模型分析
为对本文方法进行验证,我们做了模型数值实验:首先设计了一个组合模型(模型位置如图2黑色线),4个形体均为向下无限延深,磁化倾角I取90°,其它参数如表1所示.正演得到的磁异常如图2所示.

图2 理论模型正演ΔT磁异常Fig.2 Forward magnetic anomaly by theoretical model

表1 模型参数Table 1 The model parameters
为了获取四个场源的水平位置及埋深,我们采用Tilt_depth和V2D_depth方法进行对比处理,结果如图3所示.可以看出,Salem提出的Tilt_depth方法是以垂向一阶导数零值线识别边界,与真实边界存在一定误差.此外,它所反演的深度结果受旁侧异常影响很大,叠加异常可能导致多个不同的场源深度,影响结果的可靠性.例如对地质体B(如图3a所示),其±45°等值线间距(图中黑色箭头线)之一半(即场源埋深)最大值2.25km、最小值约0.79km,严重偏离了真实深度(2.5km).
图3b显示的是V2D_Depth非参数反演结果,较之Tilt_depth有显著改善.不仅识别的边界信息更清晰,所反演的深度也更接近真实深度(表1).其特征等值线之间距(即场源埋深)相对均衡,避免了Tilt_depth方法受叠加异常的影响在场源四周的反演深度不同(图3a),表明本方法受旁侧叠加异常的影响小.
为了验证方法的适应性,我们设计了向下有限延深、倾斜磁化情况时的模型,如图4所示.其中A、B、C三个棱柱体下延深度分别为2km、2km、4km,其上顶深度分别为1km,0.5km,1.5km.在磁化倾角45°,偏角0°时正演得到的ΔT磁异常如图4所示.在利用本文方法处理前,将该ΔT磁异常作化极处理,同时为了考虑计算稳定性的问题,对该异常加入了0.5%的随机干扰,处理结果见图5、6.
高阶导数的计算对高频干扰非常敏感,详见文献[18]的讨论.在本文的处理中,采用向上延拓的方式来消除高频振荡的计算问题:即在延拓后的异常基础上计算的反演深度减去相应的延拓高度.图5表示利用原平面化极磁异常与5个不同高度的延拓异常的深度反演结果,对应的V2D_depth计算结果见图6.

图3 正演磁异常非参数反演结果(a)Tilt_depth;(b)V2D_depth;黑色实线表示场源边界,黑色虚线表示计算的边界.Fig.3 Non-parameter inversion results via Tilt_depth and V2D_depth corresponding to figure 2

表2 模型反演结果对比分析Table 2 Comparison of the inversion results corresponding to different methods
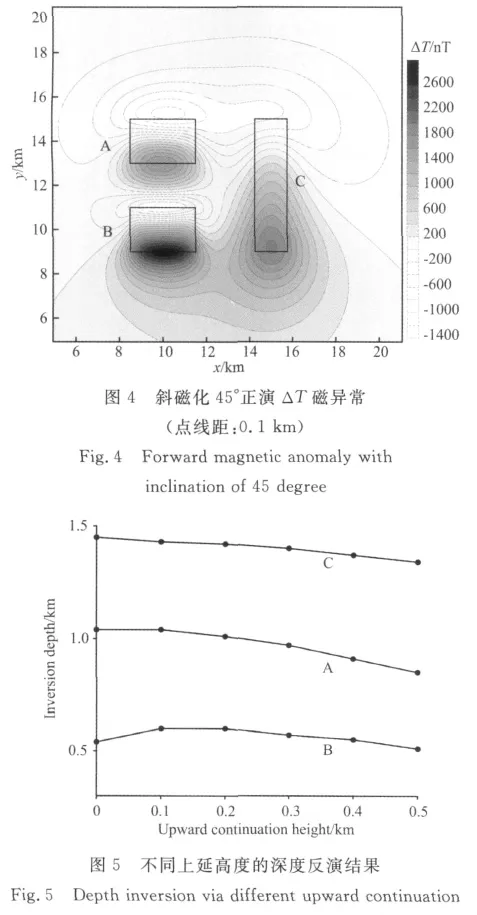
图6a中,受高频干扰的影响,由原平面磁异常计算的V2D_depth结果出现振荡现象,经过不同高度的延拓计算之后,得到的V2D_depth结果(图6b—f)消除了噪声干扰的影响,突出了异常边界与上顶深度,从反演的结果看(图5),运用5个高度的向上延拓结果计算的深度大致反映出了三个场源的深度.
为了讨论非理想模型条件下本文方法的普适性,设计了如图7所示的上顶面倾斜的直立棱柱体模型.地质体横纵长度为20km,其边界在地面的投影如图中黑色线所示.下底深度50km,上顶是一由北向南倾斜的锲型倾斜面,其北侧深度5km,南侧深度10km.垂直磁化条件下正演磁异常如图7a.图7b是对应的非参数反演结果,其中h1和h2分别表示采用±arctan(8/17)等值线间距计算的深度:分别为6km和12km.该结果表明V2D_depth方法可以突出上顶面倾斜时的倾斜面倾向.
4 实例应用
项目主要目的是了解工区内的火山岩分布,侦查可能存在的石炭系火山岩圈闭,了解石炭系地层分布情况.图8是工区构造分区图,可以看出,工区跨两个一级构造单元:乌伦古坳陷和陆梁隆起,四个二级构造单元:青格里底山凸起、索索泉凹陷、三个泉凸起以及陆南凸起.本区有2个主要磁性层:一个是分布在石炭系中的火成岩所形成的局部磁性层;另一个是深部古老结晶基底的磁性层.从磁异常特征分析,结晶基底引起区域强磁异常,而石炭系火成岩引起局部弱磁异常.

该区布设了1∶5万磁法面积测量工作,ΔT化极磁异常如图9所示.可以看出,工区磁异常总体特征为北西走向,总体上反映了海西期褶皱基底的起伏,其中东北、西南角异常高,中部存在北西向的低缓异常带.除南部有一些局部异常外,总体形态十分简单,幅值大约在-650~450nT变化.由于石炭系地层埋深较大,火成岩引起的局部异常为弱异常,其幅值只有十几至几十纳特;而前寒武强磁性结晶基底,它引起的区域异常可达上百纳特,强大的区域背景场掩盖了石炭系火成岩产生的弱磁异常.

根据地质认识,索索泉凹陷南部Ⅱ2构造单元是石炭系地层火成岩局部构造发育区.但受埋藏深度大、加之较强的背景场干扰等影响,并没有引起可以识别的磁异常.图10a是采用Tilt_depth方法获得局部异常,一定程度上突出了弱异常,但是局部场源细节模糊,尤其是受叠加异常的影响,Tilt_depth方法难以得到满意的深度反演结果,其±45°等值线并没有突出相应的信息,零值线所反应的异常边界也相对粗糙.
图10b是采用本文方法处理的结果:为了消除高频干扰,我们对磁异常上延了1km高度.该结果突出了局部异常信息:其中测区北东角(F1断裂以北)以及测区西南部(F4、F2断裂以南)的高磁异常可能反应了基底隆起的影响.从图9可以看出,对本研究区有重要意义的Ⅱ2构造单元并没有明显的磁异常显示,经过处理后(图10b),原本由火山岩引起的微弱磁异常得到体现,如图中的F5断裂与F6断裂所挟持的部位.另外,磁异常V2D_depth非参数反演也得出了深度信息,例如图10b中A异常反演的深度为1990m,B异常反演的深度为2267m(如图11所示),该反演深度与地震勘探、钻孔资料揭露的石炭系地层上顶深度相符合1)中石化西部新区勘探指挥部,准噶尔盆地青格里底山区块重、磁力、电法MT勘探重磁项目成果报告,2008.:钻井Zk01在井深1981~2894m钻遇石炭系火山沉积相凝灰岩,反应了处理结果的可靠性.因为钻孔Zk01钻遇的沉积相凝灰岩相对其它火成岩具有低磁性特征,因此在图10b中没有显示局部强磁异常.

图10 工区磁异常非参数反演结果(a)Tilt_depth方法结果;(b)V2D_depth方法结果,图中红色线表示断裂,黑色线表示零值线.Fig.10 Result of non-parametric fast inversion corresponding to Figure 9

图11 V2D_depth方法反演异常深度(图10b局部放大)Fig.11 Depth inversion of V2D_depth
对图中的 A异常或B异常,±arctan(8/17)(≈±25.2°)两条等值线间距随边界位置变化,则由此间距确定的局部场源深度也随之变化,如A异常的北边界(或B异常的东边界)处确定的局部场源深度小得多.究其原因,主要是实际问题中的局部场源顶面一般非水平且非规则曲面(对比图7上顶为倾斜面的模型示例).此外,旁侧异常的叠加也可能是引起这种场源周围特征等值线间距不均匀的原因.
5 分析与结论
在平面磁异常处理中,大多传统方法处理结果单一,并且对叠加异常计算效果欠佳,尤其是难以获取受背景场覆盖的局部弱异常信息.本文根据“化极磁异常在垂直物性边界正上方具有梯度极大”的特点进行异常识别,在此基础上根据Nabighian提出的通用磁场梯度公式,推导了基于磁异常高阶导数的非参数反演算法,可以同时获得场源边界以及深度反演结果.为了避免导数计算引起的计算振荡,建议采用向上延拓的处理方法,消除高频振荡.理论模型与实际应用表明,本文方法可以获得较好的结果,同时通过一组上顶面非水平的模型试验说明了该方法可以反映倾斜面的不同深度,以此指导实际应用中模型上顶面倾向的判断.较之Tilt_depth方法,本文方法具有以下特点:
(1)V2D_depth可以同时获得场源边界与埋深信息,且能够实现微弱异常的分析.
(2)相比Tilt_depth方法以垂向一阶导数零值点确定场源边界,V2D_depth方法能获得更好的分析效果.
(3)Tilt_depth方法的应用瓶颈是它对复杂的叠加异常分析效果欠佳:叠加异常导致Tilt_depth在场源四周的特征等值线间距存在很大差别,这意味着深度参数计算的不确定性.而V2D_depth方法在一定程度上克服了这种缺点,模型试验及实际数据处理表明本文方法受叠加异常的影响小,并且获得的场源边界及深度参数都更接近于客观情况.
(4)关于数值奇异的问题.Tilt方法在异常极大值处水平导数值为零,即分母为零计算产生数值奇异;而本文方法,如公式(9),产生奇异的前提是垂向二阶导数与垂向导数的水平导数同时为零,这种情况在异常区是不可能的.此外,即使出现分母为零的情况,因为分子部分也是零,所以比值结果为1.分析之,即本文方法不会像Tilt_depth方法出现数值奇异的问题.
通过以上分析,本文提出的磁异常非参数快速反演方法,计算简单实用,对不同强度的异常、叠加异常都能够获得理想的分析结果,并通过理论模型及实践应用证明了方法的有效性.
致 谢 本文得到了评审专家中肯的建议,并为论文的完善提供了大量有价值的修改意见,笔者向两位匿名评审专家致以谢意!
(References)
[1]管志宁.地磁场与磁力勘探.北京:地质出版社,2005.Guan Z N.Geomagnetic Field and Magnetic Exploration(in Chinese).Beijing:Geological Publishing House,2005.
[2]Salem A,Williams S,Fairhead J,et al.Tilt-depth method:A simple depth estimation method using first-order magnetic derivatives.The Leading Edge,2007,26(12):1502-1505.
[3]Miller H G,Singh V.Potential filed tilt—a new concept for location of potential field sources.Journal of Applied Geophysics,1994,32(2-3):213-217.
[4]Salem A,William S,Fairhead D,et al,Interpretation of magnetic data using tilt-angle derivatives.Geophysics,2008,73(1):L1-L10.
[5]Lee M,Morris W,Ugalde H.Amplitude effects of magnetic signals on depth estimations.11th SAGA biennial technical meeting and exhibition,Swaziland,2009,16-18,276-279.
[6]Lahti I,Karinen T.Tilt derivative multiscale edges of magnetic data.The Leading Edge,2010,29(1):24-29.
[7]Fairhead J D,Salem A,Cascone L,et al.New developments of the magnetic tilt-depth method to improve structural mapping of sedimentary basins.Geophysical Prospecting,2011,59(6):1072-1086.
[8]OruçB,Selim H H.Interpretation of magnetic data in the Sinop area of Mid Black Sea,Turkey,using tilt derivative,Euler deconvolution,and discrete wavelet transform.Journal of Applied Geophysics,2011,74(4):194-204.
[9]Valléel M A,Smith R S,Keating P.Metalliferous mining geophysics—State of the art after a decade in the new millennium.Geophysics,2011,76(4):W31-W50.
[10]White J C,Beamish D.Magnetic structural information obtained from the HiRES airborne survey of the Isle of Wight.Proceedings of the Geologists′Association,2011,122(5):781-786.
[11]Smith R S,Thurston J B,Salem A,et al.A grid implementation of the SLUTH algorithm for visualising the depth and structural index of magnetic sources.Computers &Geosciences,2012,44:100-108.
[12]郑伟军.Tilt导数方法研究及其在重磁数据处理中的应用[硕士论文].北京:中国地质大学,2010.Zheng W J.Research on Tilt derivative and application in processing gravity and magnetic data [Master thesis](in Chinese).Beijing:China University of Geosciences,2010.
[13]王想,李桐林.Tilt梯度及其水平导数提取重磁源边界位置.地球物理学进展,2004,9(3):625-630.Wang X,Li T L.Locating the boundaries of magnetic or gravity sources with tdrand tdr-thdrmethods.Progress in Geophysics(in Chinese),2004,9(3):625-630.
[14]郭华,熊盛青,于长春.Tilt-depth方法的应用.物探与化探,2009,33(5):583-586.Guo H,Qing S X,Yu C C.The application of tilt-depth technology.Geophysical and Geochemical Exploration(in Chinese),2009,33(5):583-586.
[15]郭华,于长春,吴燕冈.改进的斜导数方法及应用.物探与化探,2009,33(2):212-216.Guo H,Yu C C,Wu Y G.An improved tilt derivative method and its application.Geophysical and Geochemical Exploration (in Chinese),2009,33(2):212-216.
[16]Nabighian M N.The analytic signal of two-dimensional magnetic bodies with polygonal cross-section:its properties and use for automated anomaly interpretation.Geophysics,1972,37(3):507-517.
[17]张恒磊.现代信号处理的位场滤波方法[博士论文].武汉:中国地质大学,2011.Zhang H L.Potential field data filtering via modern signal processing[Ph.D.thesis](in Chinese).Wuhan:China University of Geosciences,2011.
[18]张恒磊,刘天佑,杨宇山.各向异性标准化方差计算重磁源边界.地球物理学报,2011,54(7):1921-1927.Zhang H L,Liu T Y,Yang Y S.Calculation of gravity and magnetic source boundary based on anisotropy normalized variance.Chinese J.Geophys.(in Chinese),2011,54(7):1921-1927.

