杨氏模量和泊松比反射系数近似方程及叠前地震反演

宗兆云，印兴耀，张 峰，吴国忱

1 中国石油大学（华东）地球科学与技术学院，青岛 266555

2 中国石油大学（北京）地球物理与信息工程学院，北京 102249

1 引 言

地震波纵横波速度、岩石纵横波模量、拉梅参数、体积模量及泊松比等弹性参数在油气储层预测和流体识别中发挥了重要作用.叠前地震反演是从叠前地震资料中获取此类弹性参数的主要方法.由于正演算法不同，叠前地震反演可以分为基于射线追踪和Zoeppritz方程及其近似的AVO反演和基于全波波动方程的全波形反演.地震全波形反演不仅能够利用地震波传播的走时和振幅特性，还能够自动考虑地震波传播过程中的反射、透射、散射、绕射、多次波、波型转换等问题，而不局限于只利用反射波信息，充分利用地震波场的全波形特征，实现介质弹性参数直接反演，但由于其计算效率和分辨能力有限，目前主要用于地震速度建模.相比全波形反演，AVO反演能够综合测井等多尺度资料的信息，其在储层预测和流体识别方面的高效性及高分辨率特征，一直备受人们青睐[1-3］.

Zoeppritz方程是AVO反演的基础，但由于该方程具有较强的非线性，人们更多地采用其各种近似方程进行 AVO反演[4-5］.Aki和Richard[6］基于微扰理论和界面两侧介质参数弱变化近似条件下推导得到基于纵横波速度和密度的纵波反射系数近似方程.Shuey[7］建立了基于泊松比、横波速度和密度的反射系数近似方程，该方程在含气储层AVO分析中发挥了重要作用，但由于该方程中泊松比项具有非线性特征，很少用于AVO反演.为提高参数反演稳定性，Fatti等[8］推导了基于纵横波阻抗和密度的反射系数近似方程，该方程能够更稳定地反演得到纵横波阻抗参数.为直接获取流体敏感参数，Goodway等[9］和 Russell等[10］分别推导了基于拉梅参数和流体因子的反射系数近似方程，并实现了从叠前地震资料中直接提取拉梅参数和流体因子.

基于反射系数近似方程，Fatti等[8］用权叠加的方法得到了纵波阻抗的相对变化量和横波阻抗的相对变化量，进而计算得到绝对纵横波阻抗.Simmons和Backus[11］应用线性化的反演方法求取纵波阻抗、横波阻抗和密度反射系数，反演过程中采用Gardner[12］的纵波速度与密度的经验关系式和Castagna[13］的关于纵波与横波速度的经验方程.Buland和Omre[14］研究了基于贝叶斯理论的线性AVO反演方法，直接反演得到纵波速度、横波速度和密度参数，但该方法没有建立参数之间的关系.Yin等人[15］在考虑了参数去相关情况下提出了点约束稀疏脉冲叠前地震反演，直接反演得到纵横波速度和密度参数.通过对反射系数方程转换到对数域，并进行简单推导，Connolly[16］首先提出弹性阻抗（EI）的概念，并有学者认为EI在抗噪能力方面比叠前 AVO 反 演 有 优 势[17］.Yin 等[18］提 出 利 用Connolly弹性阻抗方程从三个角度反演结果中通过计算提取纵、横波速度和密度参数的方法，进而可以计算得到纵、横波阻抗，拉梅常数，泊松比等丰富多样的岩性参数，从而进行地下储层的展布情况及含油气性预测.Wang等[19］针对Zoeppritz方程的Gray近似[20］作了弹性阻抗方程的推导，并实现了从EI反演中直接提取拉梅常数，降低了间接计算带来的累积误差.

随着常规油气资源获取难度的增大，全球油气勘探已进入了常规与非常规油气并重发展的时代.页岩气作为全球重要接替资源，其勘探开发技术成为目前人们的研究热点和难点.页岩气是指赋存于页岩中的非常规气.储集空间以裂缝为主并可以吸附气和水溶气形式赋存，在裂缝发育带可获较高产量.页岩储层的基质渗透率较低，需要裂缝才能形成工业产能.除本身的天然裂缝外，在开发过程中还应考虑页岩储层在加砂压裂改造时，是否易于被改造.脆性越大，越易被改造.地震岩石物理研究表明，杨氏模量和泊松比能够较好地表征岩石的脆性，评价页岩储层的造缝能力，页岩气“甜点”具有高杨氏模量和低泊松比特征[21］.本文推导得到一种基于杨氏模量和泊松比的新的反射系数近似方程，并建立了一种稳定获取杨氏模量和泊松比的叠前地震直接反演方法.

2 YPD反射系数近似方程推导

1980年，Aki和Richards提出了基于纵横波速度和密度的Zoeppritz近似公式为

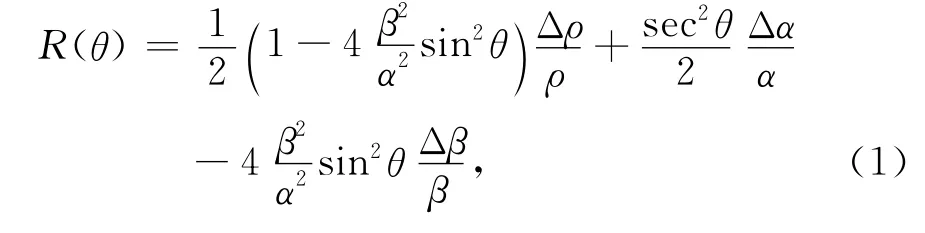
其中，α、β分别为纵、横波速度，ρ为密度，θ为入射角，Δα／α、Δβ／β、Δρ／ρ分别是纵、横波速度反射系数和密度反射系数.

由方程（1）出发，Zong等[23］建立反射系数与纵横波模量和密度的关系式如下：

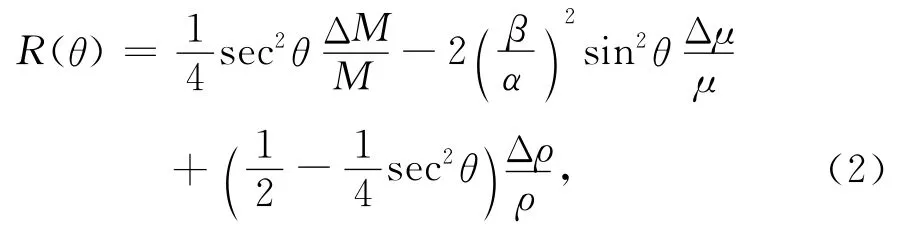
其中，M为纵波模量，与介质抗压缩性和硬度直接相关，体现储层骨架和流体信息.μ为横波模量，与介质抗剪切性和刚度直接相关，体现储层骨架信息[24］.ΔM／M、Δμ／μ分别为纵、横波模量反射系数.

在各向同性介质中，纵、横波模量与杨氏模量和泊松比关系为

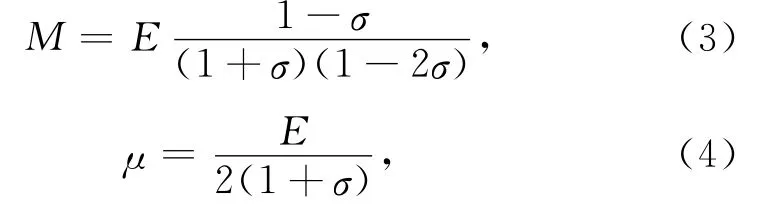
令

随着我国信息化技术的不断发展，许多银行在日常的运营过程中也都已经运用计算机技术来形成了自身的数据库管理系统，其对于银行管理水平的提升也有着非常重要的意义。但是目前许多银行在信息化技术的应用以及建设过程中还存在有比较多的安全问题，并直接威胁到了该银行的持续稳定发展。针对这一问题，也就要求各银行能够在已有基础上来对信息化管理系统以及数据库系统进行不断的更新与优化，来促使自身的信息管理能力得到进一步的提升。只有在结合客户实际需求的基础上进行信息的准确把握跟及时决策，才能够给用户进行全方位金融服务的有效提供。

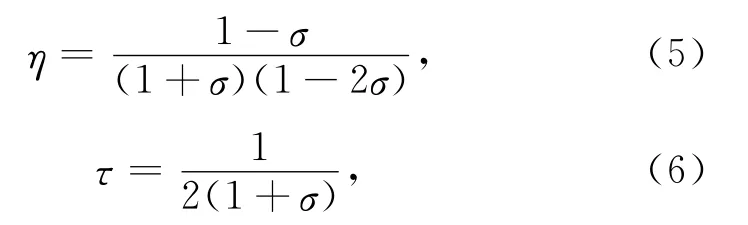
则由方程（3）和方程（5）得

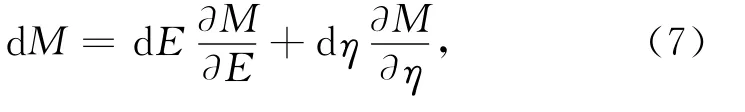
方程（7）两边同除以纵波模量可得

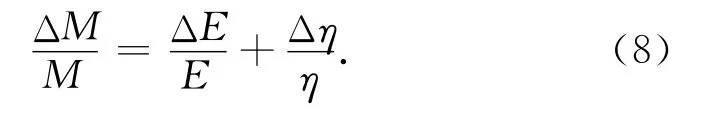
同理，由方程（4）和方程（6）得

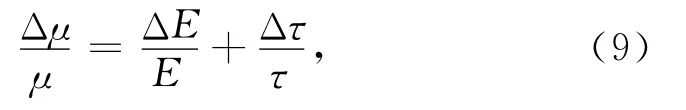
令

由方程（5）、（6）和（10）可得

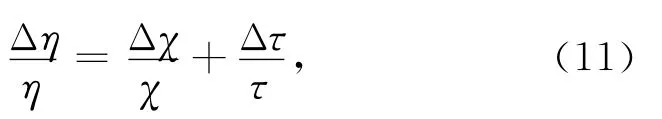
又

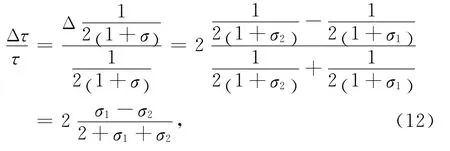
其中，σ1和σ2分别为上下层介质泊松比.同理，

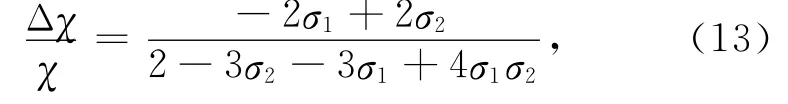
由于

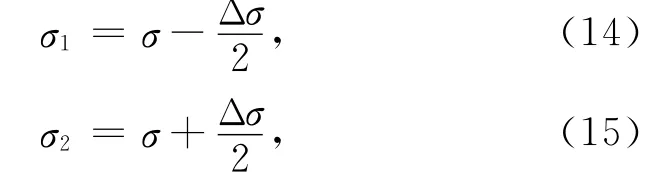
方程（14）和（15）分别代入方程（12）和（13）可得

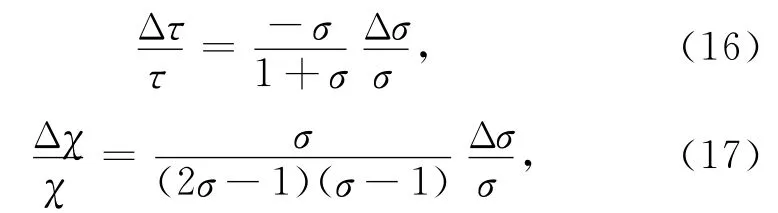
令

则

将方程（8）、（9）、（11）、（16）、（17）、（18）和（19）代入方程（2）可得

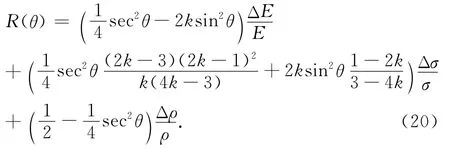
方程（20）建立了纵波反射系数与杨氏模量反射系数、泊松比反射系数及密度反射系数的线性关系.我们称之为YPD近似方程.

3 YPD近似方程精度分析

利用Goodway等[9］根据实测资料给出的含气砂岩模型，我们对利用YPD近似方程、精确Zoeppritz方程和Aki-Richards近似方程计算反射系数的精度进行了分析，模型参数见表1.

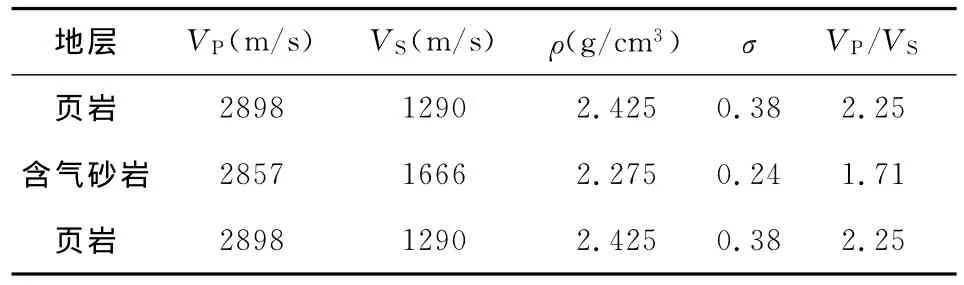
表1 Goodway（1997）[9］三层含气砂岩与页岩模型Table 1 Model for gas-bearing sandstone and shale designed by Goodway（1997）[9］

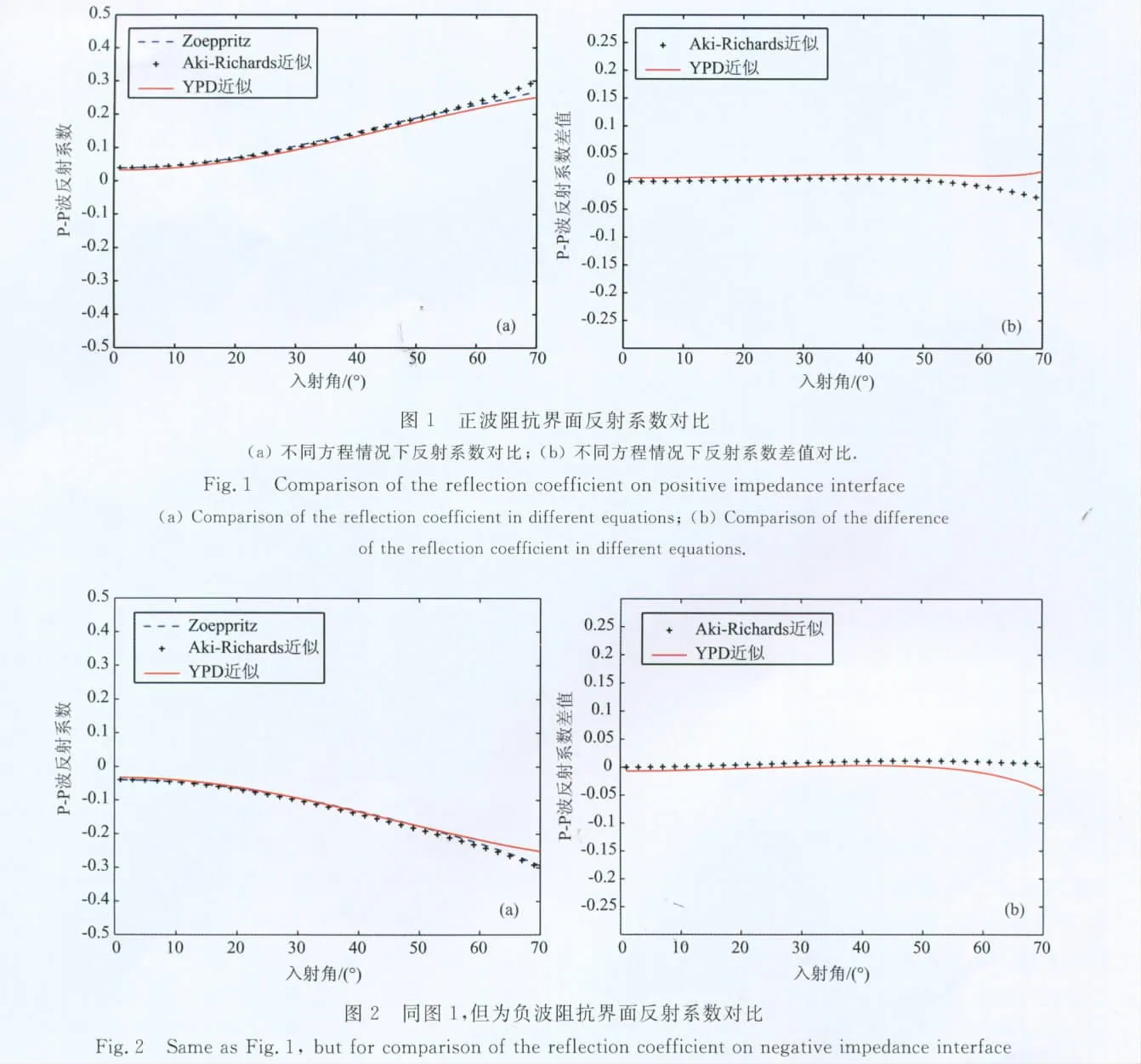
入射介质波阻抗小于透射介质波阻抗的界面称为正波阻抗界面，反之称为负波阻抗界面.上述模型中，上覆页岩、下伏含油气砂岩的反射界面就是负波阻抗界面，而上覆砂岩、下伏页岩的反射界面为正波阻抗界面.以上述模型为基础，分别用精确的Zoeppritz方程、Aki-Richards近似方程、YPD近似方程计算了不同界面处的反射系数及近似方程与精确方程的残差.图1和图2分别为正负波阻抗界面对比分析，图1a、图2a为分别用精确的Zoeppritz方程、Aki-Richards近似方程、YPD近似方程计算得到的反射系数随入射角的变化，图1b、图2b为Aki-Richards近似方程、YPD近似方程计算得到反射系数与精确方程计算得到的反射系数的差值随入射角的变化.由图可知，基于YPD近似方程得到的反射系数在入射角为40°左右仍与精确Zoeppritz方程有较好的近似，能够适用于较大角度入射情况下反射系数的准确求解.

4 YPD-AVA叠前地震反演

以方程（20）为基础，在贝叶斯反演框架下，假设待反演杨氏模量、泊松比及密度反射系数服从柯西分布，该分布假设可以最大限度提高反演分辨率[25-26］，假设似然函数服从高斯分布，同时在反演目标函数中加入初始模型约束，并通过初始模型建立各道去相关矩阵，消除待反演参数间的互相关性，建立了一种YPD-AVA叠前地震反演方法，具体反演流程如图3所示.

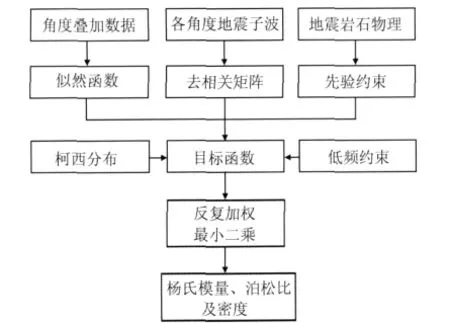
图3 YPD-AVA叠前地震反演流程图Fig.3 Flow chart for YPD-AVA pre-stack seismic inversion

贝叶斯框架下，待反演参数θ的后验概率分布为

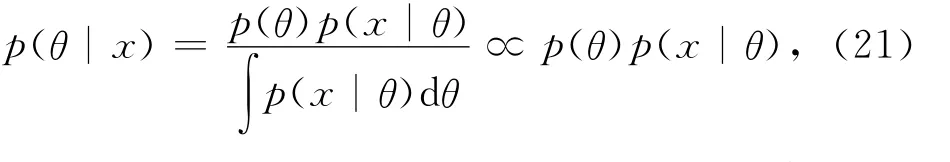
其中：θ为待反演参数，x为观测样本，p（θ｜x）为后验概率密度，p（θ）为先验概率密度，p（x｜θ）为似然函数.

贝叶斯估计由带噪声的叠前部分角度叠加道集数据D估计待反演参数（杨氏模量、泊松比与密度的反射系数）矩阵R′.假设似然函数服从高斯分布为

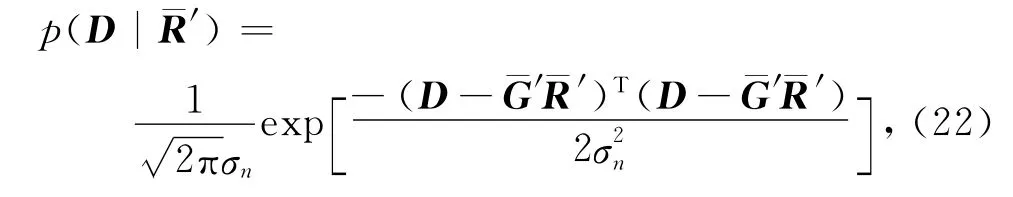
相比高斯分布，待反演参数的柯西分布在提高反演分辨能力等方面更有优势，因此，我们假设待反演参数服从柯西分布：

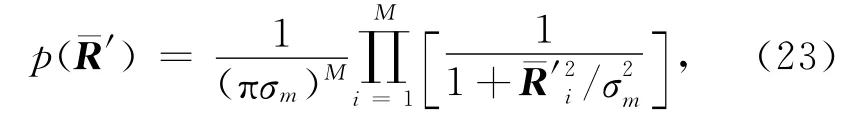
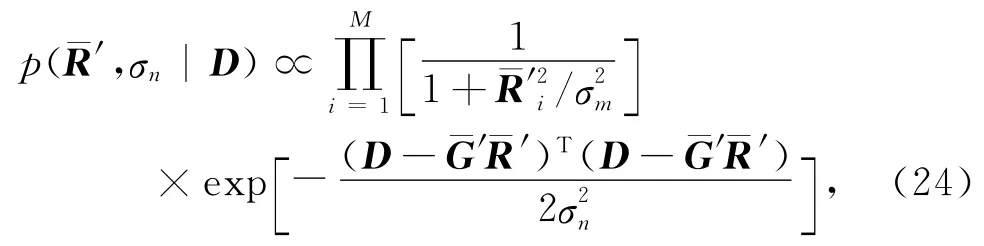
最大化后验概率分布（24）得到初始目标函数为：

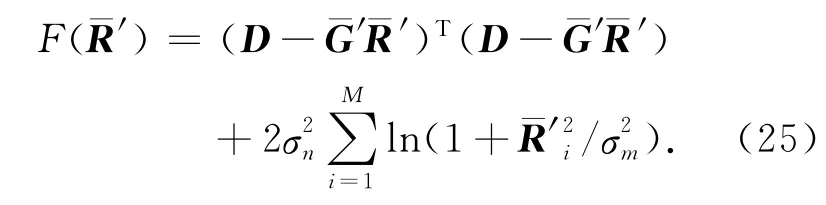
在目标函数（25）的基础上加入初始模型约束，目标函数变为：

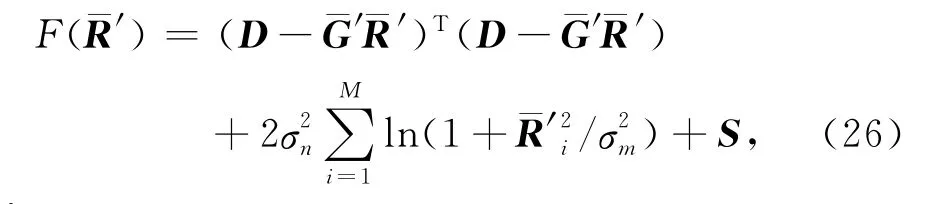
其中：

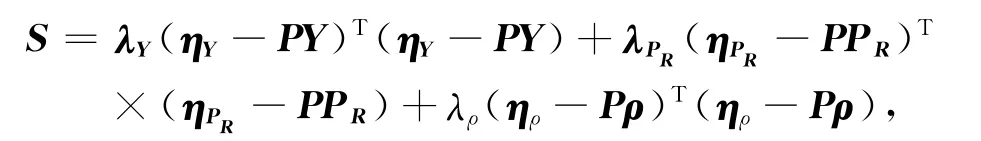
λY，λPR和λρ分别为杨氏模量、泊松比和密度约束系数，P为

方程（26）具有弱非线性，可采用反复加权最小二乘（IRLS）[27］算法进行优化求解.

5 模型验证

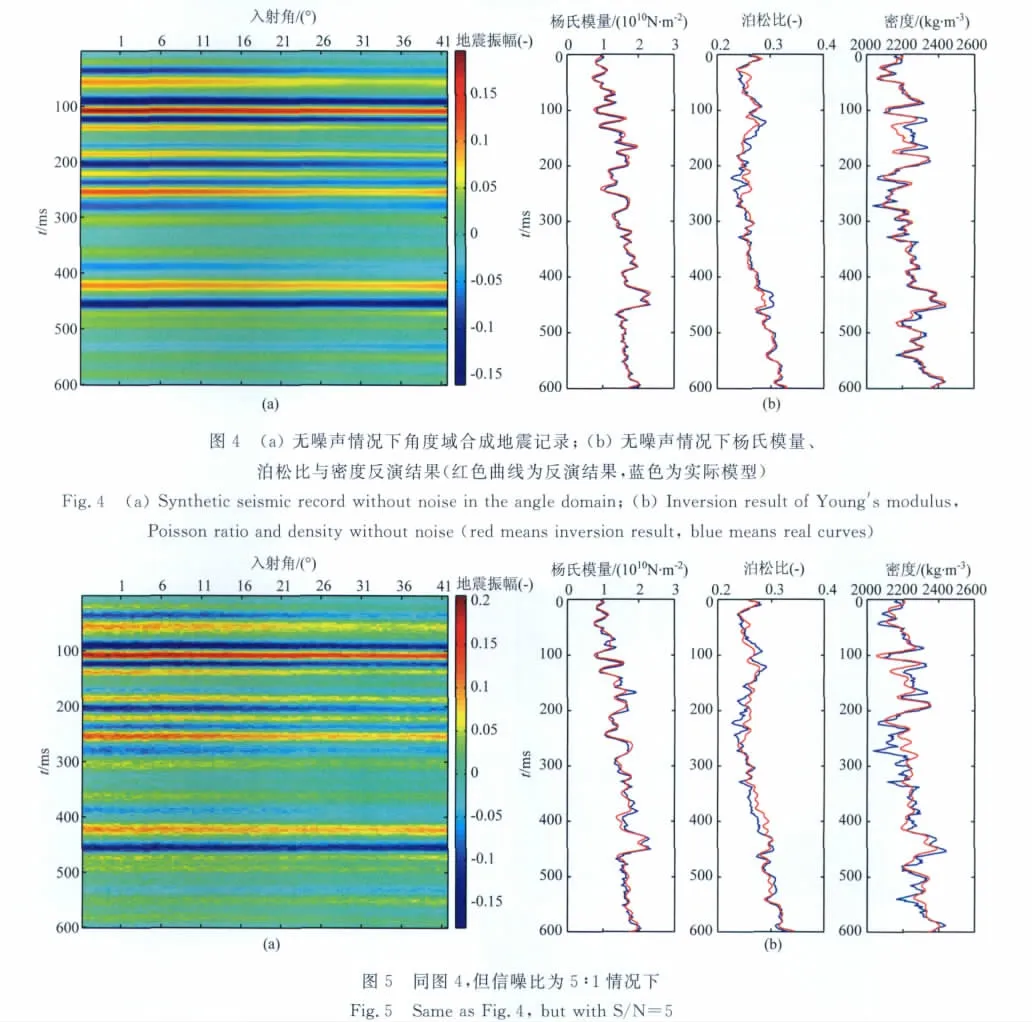
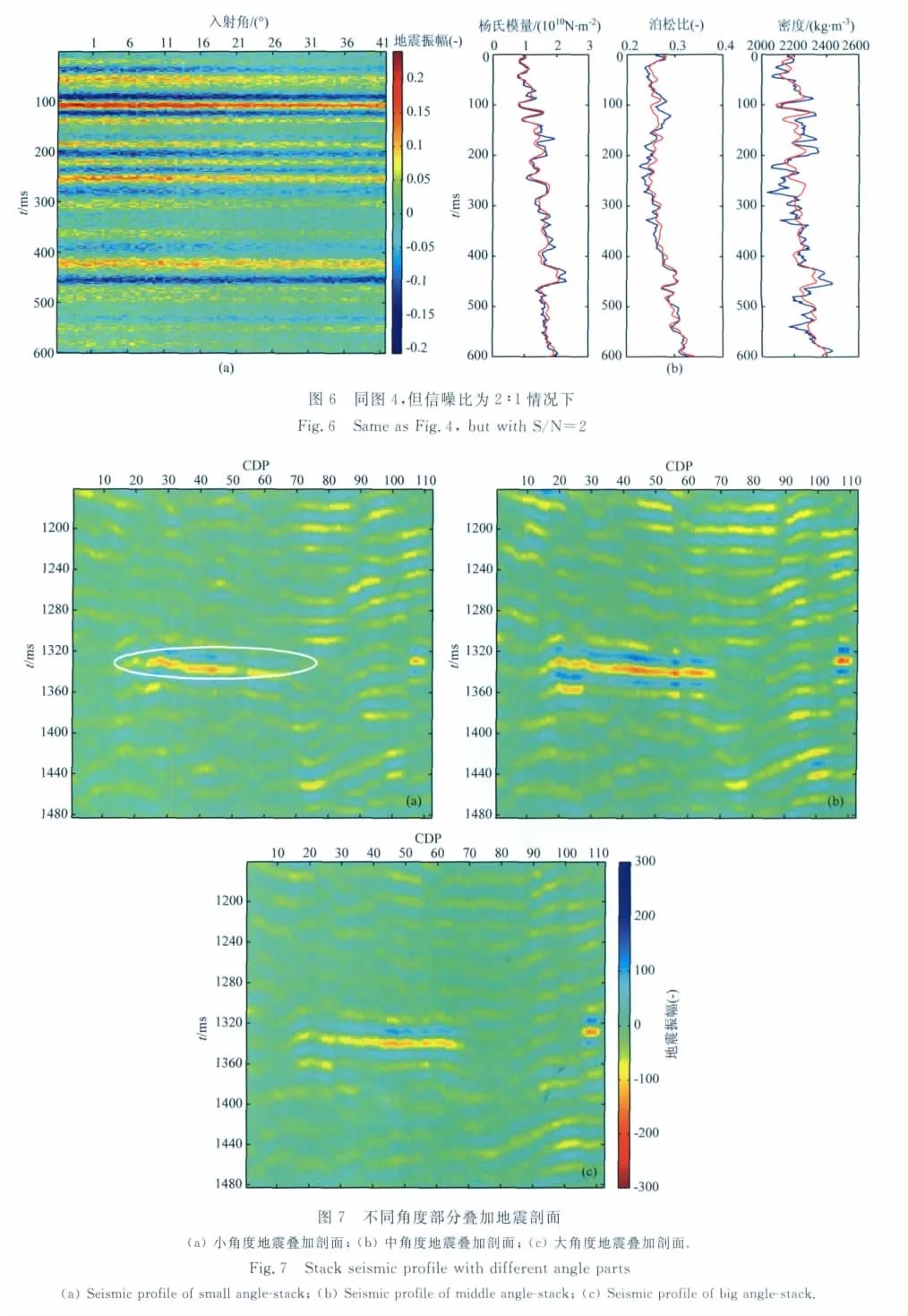
为验证YPD-AVA叠前地震反演的可行性和稳定性，本文采用实际单井模型进行验证.模型测试中采用主频为40Hz的雷克子波.图4b中蓝色曲线为某工区通过实际测井资料计算并通过深时转换得到的时间域杨氏模量、泊松比和密度曲线，采用精确Zoeppritz方程进行正演得到角度域叠前角度道集，然后利用本文提出的YPD-AVA叠前地震反演方法实现杨氏模量、泊松比和密度参数反演.图4a和图4b分别为无噪声情况下角度域合成地震记录及杨氏模量、泊松比和密度参数反演结果，其中红色曲线为反演结果，反演结果表明，无噪声情况下，该方法能够获取与真实值基本吻合的杨氏模量、泊松比和密度，验证了方法的可行性.为进一步验证方法的稳定性，对合成道集加不同程度的服从高斯分布的随机噪声，图5—图6依次是信噪比为5∶1和2∶1情况下的角度域合成地震记录与反演结果，可以看出，在加噪情况下，杨氏模量和泊松比反演结果仍与真实值有较高的吻合度，但密度反演结果在局部有些不合理，这是因为密度项对反射系数值的影响较小，在使用AVO近似公式进行反演时，很难在含噪声情况下获取合理的密度参数[28-29］.

6 实际资料试处理

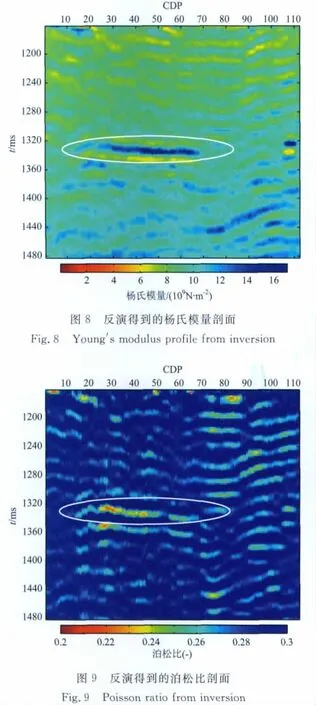
实际资料来自中国陆上某勘探工区，进行叠前地震反演之前，需要对地震数据进行保幅处理，包括精细的波前扩散补偿、震源组合与检波器组合效应的校正、反Q滤波、地表一致性处理、叠前去噪处理、去除多次波等，并假设处理后的层间多次波、各向异性的影响可以忽略不计[30］.笔者利用本文提出的YPD-AVA叠前地震反演方法对不同角度叠加剖面进行了实际资料试处理.本文反演方法输入的是部分角度叠加剖面，首先根据已知的速度信息，将叠前CMP或CRP偏移距道集转换到角度域[14］，然后，根据实际入射角范围，进行分角度叠加，提高资料信噪比.图7a、7b和7c分别是小、中、大三个角度部分叠加剖面，图中白色椭圆区域为气藏发育区.图8为反演得到的杨氏模量剖面，在含气区域呈高值异常显示，图9为反演得到的泊松比剖面，在含气区域呈低值异常显示，该反演结果与实际钻遇结果吻合较好，验证了方法的有效性.

7 结 论

杨氏模量和泊松比能够较好地表征岩石的脆性，评价页岩储层的造缝能力，页岩气“甜点”具有高杨氏模量和低泊松比特征，利用叠前地震反演获取杨氏模量和泊松比参数成为利用叠前地震资料进行页岩气“甜点”识别的重要手段.本文在平面纵波入射条件下，由Aki-Richards近似出发，推导得到基于杨氏模量、泊松比和密度的Zoeppritz近似公式（YPD近似方程），奠定了叠前反演获取杨氏模量和泊松比的理论基础.在YPD近似方程基础上建立了一种稳定反演杨氏模量和泊松比的方法，模型测试表明，该方法在信噪比比较低的情况下仍能得到合理的反演结果，实际资料试处理验证了该方法在实际生产中的可行性，提供了一种从地震数据中直接提取杨氏模量和泊松比的叠前地震反演方法.与常规AVO方法类似，该方法建立在水平层状假设基础之上，且在中等入射角情况下具有较高精度.地震岩石物理研究表明，在实际页岩气地震识别中，除进行地层岩石的脆性评价外，还需通过地层应力参数等评价页岩气地层可压裂性，因此下一步有必要建立地震反射系数与地层应力等参数间的直接关系，并发展合理的叠前反演方法，以便更好地进行页岩气藏地震识别与评价.

（References）

[1]彭苏萍，高云峰，杨瑞召等.AVO探测煤层瓦斯富集的理论探讨和初步实践——以淮南煤田为例.地球物理学报，2005，48（6）：1475-1486.Peng S P，Gao Y F，Yang R Z，et al.Theory and application of AVO for detection of coalbed methane——A case from the Huainan coalfield.Chinese J.Geophys.（in Chinese），2005，48（6）：1475-1486.

[2]牛滨华，文鹏飞，温宁等.基于BSR的AVO正演估算水合物含量方法的研究.地球物理学报，2006，49（1）：143-152.Niu B H，Wen P F，Wen N，et al.Estimation of hydrate concentration based on AVO modeling of BSR.Chinese J.Geophys.（in Chinese），2006，49（1）：143-152.

[3]彭真明，李亚林，魏文阁等.粒子滤波非线性AVO反演方法.地球物理学报，2008，51（4）：1218-1225.Peng Z M，Li Y L，Wei W G，et al.Nonlinear AVO inversion using particle filter.Chinese J.Geophys.（in Chinese），2008，51（4）：1218-1225.

[4]李景叶，陈小宏，郝振江等.多波时移地震AVO反演研究.地球物理学报，2005，48（4）：902-908.Li J Y，Chen X H，Hao Z J，et al.A study on multiple timelapse seismic AVO inversion.Chinese J.Geophys.（in Chinese），2005，48（4）：902-908.

[5]陈建江，印兴耀.基于贝叶斯理论的AVO三参数波形反演.地球物理学报，2007，50（4）：1251-1260.Chen J J，Yin X Y.Three-parameter AVO waveform inversion based on Bayesian theorem.Chinese J.Geophys.（in Chinese），2007，50（4）：1251-1260.

[6]Aki K，Richards P G.Quantitative Seismology（2ed）.San Francisco：W.H.Freeman，1980：158-164.

[7]Shuey R T.A simplification of the Zoeppritz equations.Geophysics，1985，50（4）：609-614.

[8]Fatti J L，Smith G C，Vail P J，et al.Detection of gas in sandstone reservoirs using AVO analysis：A 3-D seismic case history using the Geostack technique.Geophysics，1994，59（9）：1362-1376.

[9]Bill G，Chen T W，Downton J.Improved AVO fluid detection and lithology discrimination using Lame′s petrophysical parameters：“λρ”，“μρ”，&“λ／μfluid stack”，from P and S inversions.SEG Technical Program Expanded Abstracts，1997，16（1）：183-186.

[10]Russell B H，Gray D，Hampson D P.Linearized AVO and poroelasticity.Geophysics，2011，76（3）：C19-C29.

[11]Simmons J L，Backus M M.Waveform-based AVO inversion and AVO prediction-error.Geophysics，1996，61（6）：1575-1588.

[12]Gardner G H F，Gardner L W G，Gregory A R.Formation velocity and density-the diagnostic basics for stratigraphic traps.Geophysics，1974，39（6）：770-780.

[13]Castagna J，Batzle M，Eastwood R L.Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks.Geophysics，1985，50（4）：571-581.

[14]Arild B， More H.Bayesian linearized AVO inversion.Geophysics，2003，68（1）：185-198.

[15]Yin X Y，Yang P J，Zhang G Z.A novel prestack AVO inversion and its application.SEG Technical Program Expanded Abstracts，2008，27（1）：2041-2045.

[16]Connolly P.Elastic impedance.The Leading Edge，1999，18（4）：438-452.

[17]Guillaume C.AVO inversion and elastic impedance.SEG Technical Program Expanded Abstracts，2000，19（1）：142-145.

[18]Yin X Y，Yuan S H，Zhang F C.Rock elastic parameters calculated from elastic impedance.CPS／SEG Technical Program Expanded Abstracts，2004：538-542.

[19]Wang B L，Yin X Y，Zhang F C.Laméparameters inversion based on elastic impedance and its application.Applied Geophysics，2006，3（3）：174-178.

[20]Gray D， Verttas D G C.Elastic inversion for Lame parameters.SEG Technical Program Expanded Abstracts，2002，21（1）：213-216.

[21]Sena A，Gabino C，Chesser K，et al.Seismic reservoir characterization in resource shale plays： “Sweet spot”discrimination and optimization of horizontal well placement.SEG Technical Program Expanded Abstracts，2011，30（1）：1744-1748.

[22]Goodway B，Perez M，Varsek J，et al.Seismic petrophysics and isotropic-anisotropic AVO methods for unconventional gas exploration.The Leading Edge，2010，29（12）：1500-1508.

[23]Zong Z Y，Yin X Y，Wu G C.Robust AVO inversion for elastic modulus and its application in fluid factor calculation.SEG Technical Program Expanded Abstracts，2011，30（1）：406-411.

[24]Mavko G， Mukerji T，Dvorkin J.The Rock Physics Handbook：Tools for Seismic Analysis in Porous Media.Cambridge：Cambridge University Press，2009：21-25.

[25]Wubshet A，Sacchi M D.High-resolution three-term AVO inversion by means of a Trivariate Cauchy probability distribution.Geophysics，2011，76（3）：R43-R55.

[26]杨培杰，印兴耀.非线性二次规划贝叶斯叠前反演.地球物理学报，2008，51（6）：1876-1882.Yang P J，Yin X Y.Non-linear quadratic programming Bayesian prestack inversion.Chinese J.Geophys.（in Chinese），2008，51（6）：1876-1882.

[27]Daubechies I，Devore R，Fornasier M，et al.Iteratively reweighted least squares minimization for sparse recovery.Communications on Pure and Applied Mathematics，2010，63（1）：1-38.

[28]Lines L R.Density contrast is difficult to determine from AVO.Canadian Journal of Exploration Geophysics，1998.

[29]Downton J E.Seismic parameter estimation from AVO inversion[Ph.D.thesis］.Canada：University of Calgary，2005：87.

[30]宗兆云，印兴耀，吴国忱.基于叠前地震纵横波模量直接反演的流体检测方法.地球物理学报，2012，55（1）：284-292.Zong Z Y，Yin X Y，Wu G C.Fluid identification method based on compressional and shear modulus direct inversion.Chinese J.Geophys.（in Chinese），2012，55（1）：284-292.