利用Moho面起伏及地表地形数据反演岩石圈有效弹性厚度的莫霍地形导纳法（MDDF）

杨 亭，傅容珊，黄金水

蒙城地球物理国家野外科学观测研究站，中国科学技术大学地球和空间科学学院，合肥 230026

1 引 言

岩石圈有效弹性厚度Te是表征其挠曲强度和动力学响应的重要物理量[1］.在岩石圈动力学过程的研究中，需要充分考虑岩石圈有效弹性厚度的影响[2］.与此同时，根据岩石圈有效弹性厚度的变化，还可以推测地下温度或者化学成分的变化[3］.确定岩石圈有效弹性厚度有多种方法[4］，自Dorman和Lewis在1970年首次采用线性传递函数（重力地形导纳）方法估计岩石圈有效弹性厚度[5］以来，国内外许多研究者开始利用重力异常和地形数据对不同地区岩石圈的有效弹性厚度做出估计[3，6-9］.随着类地行星及月球地形和重力场观测数据的增加，利用地形和重力数据确定行星岩石圈有效弹性厚度也已成为推测行星岩石圈构造与演化历史的重要手段[10-11］.然而，长期以来有效弹性厚度的确定却一直存在着争议.在海洋地区，岩石圈有效弹性厚度基本与600℃等温线重合[1］.在大陆地区，不同作者得到的结果却差别很大：一些作者利用布格相关方法得到的克拉通地区有效弹性厚度可超过100km，并据此认为地壳和岩石圈地幔对岩石圈挠区强度均有贡献[12］；而另外一些作者利用自由空气导纳方法得到的岩石圈有效弹性厚度一般不大于地震层厚度，并据此推测，大陆岩石圈的强度主要限制在地震层，地幔在地质时间尺度上是弱的（甚至弱于下地壳），对岩石圈挠区强度贡献很小[13］.Pérez-Gussinyé等利用有效弹性厚度已知的岩石圈产生的模拟地表地形和重力异常数据，探讨了利用自由空气导纳和布格相关得到的岩石圈有效弹性厚度存在差异的原因.他们发现，两者存在差异的原因在于自由空气导纳使用有限窗口的Multitaper功率谱估计的观测响应函数和无限大窗口的理论响应函数进行比较，这导致自由空气导纳估计有效弹性厚度的值远远低于真实值.Pérez-Gussinyé据此修订了计算理论响应函数的公式，使利用自由空气导纳和布格相关得到的有效弹性厚度一致[14］.Pérez-Gussinyé等的工作为消除两种谱方法（自由空气导纳和布格相关法）反演有效弹性厚度的差异画出了比较完美的句号.然而模型研究表明，使用重力与地形数据反演岩石圈有效弹性厚度与真实值相比存在较大偏差和均方差[14］.

重力异常对地形的均衡响应本质上反映的是Moho面起伏对地形加载的均衡响应.因此，直接使用Moho面起伏代替重力数据来反演岩石圈有效弹性厚度有可能获得更高的反演精度.为此，本文提出了利用Moho面起伏及地表地形数据反演岩石圈有效弹性厚度的Moho地形导纳法（MDDF）.为了验证本文方法的可靠性，给出了简单的模型算例.该算例结果与Pérez-Gussinyé等结果[14］的比较表明，与传统的重力地形导纳法相比，使用Moho地形导纳法（MDDF），将较大地提高岩石圈有效弹性厚度的反演精度.

从图1中可以发现浒苔粉的浓度在2 g/L时，单位浒苔吸附Ni2+的量最多。浒苔浓度在18 g/L和22 g/L时，单位浒苔吸附Ni2+的量最少。从图5中可以看出，浒苔粉浓度在2 g/L时，对Ni2+的吸附效果是最低的，吸附率只有41.25%。当浒苔粉浓度在6 g/L时，对Ni2+的吸附效果是最好的，吸附率为45%。对图1和图2进行比较后，最后以浒苔粉浓度为6 g/L，即50 mL中有0.3 g作为我们下面实验所需要的浒苔粉量。

2 确定岩石圈有效弹性厚度的Moho地形导纳法（MDDF）

岩石圈有效弹性厚度Te本质上描述的是岩石圈在垂向力加载下产生挠曲变形的难易程度.岩石圈受到垂向加载后产生的弹性挠区变形叠加在初始地表地形和Moho面起伏上，便形成了最终观测到的地表地形和Moho面起伏.通常，岩石圈所受的垂向加载可分为地表加载和内部加载.由于Moho面是岩石圈内部密度差异最大的界面（密度跳跃约0.4g／cm3），其起伏将会对岩石圈作用巨大的垂向加载.一般认为，Moho面起伏导致的质量加载是岩石圈内部最大的垂向加载[15］.为了简单，本文模型假定Moho面起伏导致的质量加载是岩石圈内部的唯一垂向加载，其与地表的地形加载共同作用于岩石圈上，使岩石圈产生挠曲.

岩石圈在垂向载荷作用下的挠曲模型如图1所示（由于实际的质量加载可认为是各个周期加载的叠加，图中只画出某个周期的垂向加载）.在地表地形起伏HI导致的垂向质量加载下，岩石圈产生挠曲WT.Moho面和岩石圈-软流圈界面（LAB）的最终起伏与岩石圈的挠曲WT相同（图1（a，b））.挠曲叠加在初始地表地形之上产生均衡时的地表地形HT.假定岩石圈在挠曲过程中厚度不变，则有：

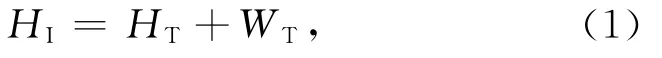
在Moho面起伏WI导致的垂向质量加载下，岩石圈产生挠曲HB，地表地形和LAB的最终起伏便为岩石圈的挠曲HB.岩石圈挠曲叠加在初始Moho面起伏上产生均衡时的 Moho面起伏WB（图1（c，d））.同样假定岩石圈挠曲过程中厚度不变，则有：

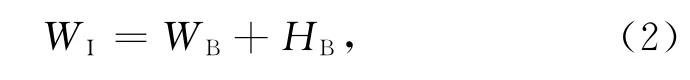
最终的岩石圈地表地形和 Moho面起伏（图1e）是HI和WI单独作用下岩石圈挠曲响应的叠加.故最终的地表地形为

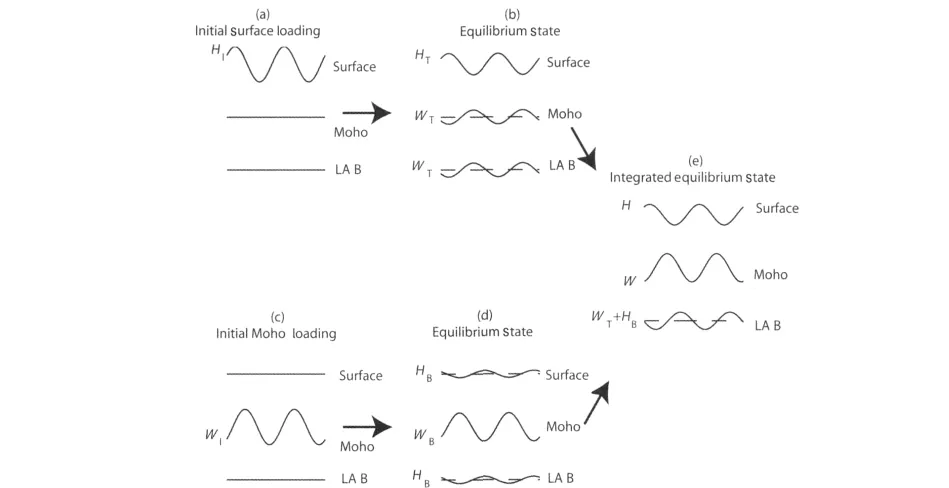
图1 岩石圈在地表地形和Moho面起伏引起的垂向正弦载荷作用下产生挠曲变形示意图.上侧实线代表地表面，中间实线代表Moho面，最下侧实线代表岩石圈软流圈分界面（LAB）.虚线代表岩石圈各界面的初始位置.参见文中详细解释Fig.1 Schematic model illustrating the deflection of the elastic lithosphere under sinusoidal topography and Moho relief loads.Surface，Moho interface and lithosphere asthenosphere boundary（LAB）are denoted by the top，middle and bottom solid lines respectively.Dashed lines represent initial locations of the interfaces.See text for details

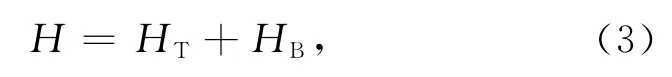
最终的Moho面起伏为

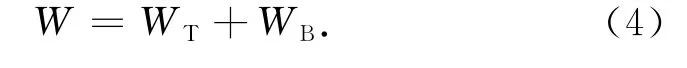
上述 公 式 中，H，HI，HT，HB向 上 为 正，W，WI，WT，WB向下为正.

根据导纳的定义，Moho面起伏对地表地形导纳的观测值为波数域中Moho面起伏与地表地形的比：

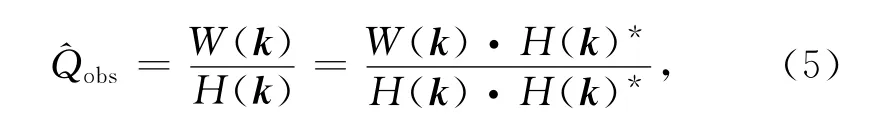
其中H（k）＊表示H（k）的复共轭.

理学的建构使得原有的忠君观念上升到了“理”的高度，相较于先秦儒家的“以道事君，不可则止”、“从道不从君”来说，更显得苛刻。更何况靖康之后，国破家亡的切身之痛，使得忠奸之分、华夷之辩更加激烈，在这样的背景下，冯道无可避免地成为批判的标靶。

为了反演岩石圈有效弹性厚度，需要将观测导纳曲线与理论导纳曲线（有效弹性厚度的函数）进行拟合.与观测导纳拟合的最好的理论导纳所对应的有效弹性厚度便为反演结果.

根据挠曲方程，如果我们已知某个区域岩石圈的有效弹性厚度Te、初始的地表和Moho面垂向质量加载（以地形起伏HI和WI表示），便能够得到均衡时的HT，WT，HB，WB.因此，公式（3），（4）实际上就是H，W 和HI，WI及有效弹性厚度Te的关系式.如果我们假定岩石圈的有效弹性厚度为某一值，便可根据观测地表地形起伏H和Moho面的起伏W 得到理论的HI，WI和 HT，WT，HB，WB.然后带入公式（5）可得到下面的理论导纳公式：

类似于重力地形导纳，可称这种方法为Moho地形导纳法（MDDF）.

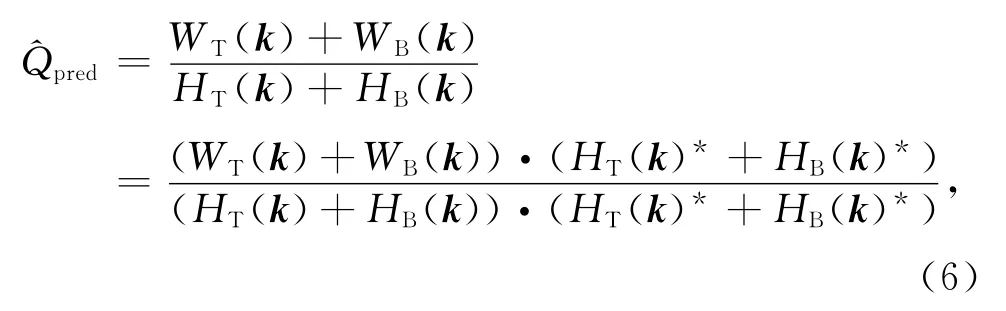
改变Te，便可以得到不同的＾Qpred.与观测导纳＾Qobs拟合的最好的＾Qpred对应的有效弹性厚度便为反演结果.

上式中，w（X）为均衡时弹性板挠曲，向下为正；q（X）为均衡时弹性板受到的垂向载荷，向下为正；为挠曲强度.其中，E为杨氏模量，Te为岩石圈有效弹性厚度，ν为泊松比，本文中模型所采用的物理参数列在表1中.

2.1 岩石圈对地表加载HI的均衡响应

如图1（a，b）所示，岩石圈在某一地表地形的垂向加载下产生挠曲.如果地壳和地幔岩石圈耦合在一起，则Moho面在垂向加载作用下的起伏即为岩石圈的挠曲.

弹性板在垂向作用力下的挠曲公式[16］为

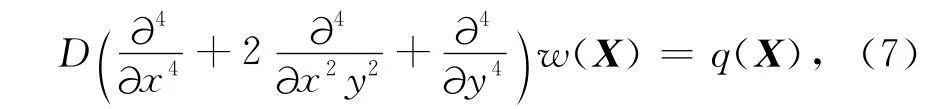
下面我们首先回顾岩石圈分别对地表及Moho面加载HI，WI的均衡响应，然后对其叠加得到一定弹性厚度下，岩石圈的地表及Moho面地形H，W和初始加载HI，WI的转换关系.最后给出计算理论Moho地形导纳的公式.

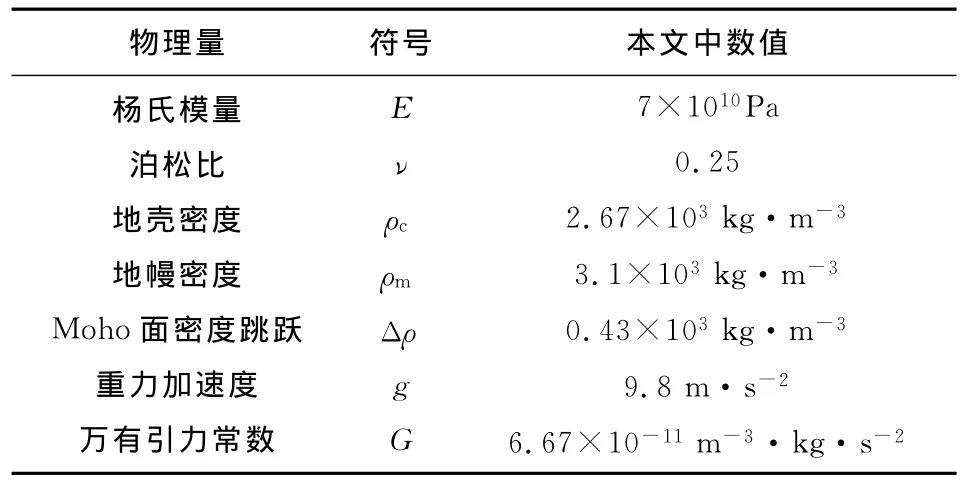
表1 文中物理参数的符号及数值Table 1 Symbols and values of physical parameters in this article

对于大陆岩石圈，假定初始有地形加载q0（X）=ρcghi（x），式中ρc为大陆地壳密度，g为重力加速度，hi为初始地表地形，向上为正.在地表地形载荷q0（X）=ρcghi（x）的作用下，岩石圈会发生挠曲，在挠曲均衡时，地表起伏为ht，Moho面起伏为wt.由于Moho面上下有密度差，在均衡时，岩石圈会受到向上的作用力Δρgwt（X），其中Δρ为Moho面密度跳跃.则在均衡时的大陆岩石圈的挠曲方程为：

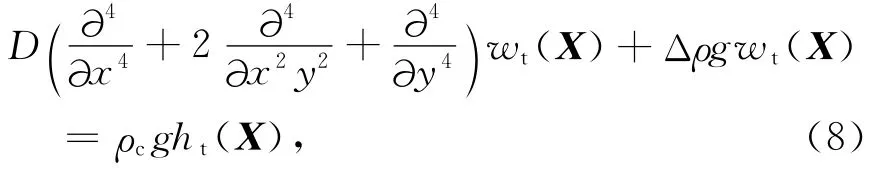
对上式进行傅里叶变换得到

计算得到的模拟地表和Moho深度观测值如图2（g，h）所示.为了将其与实际地形及 Moho面起伏进行联系.对地表地形起伏加上2km的平均地形，对Moho面起伏加上40km的平均深度.从图2（g，h）可见，由于岩石圈均衡调整的作用，虽然初始地表起伏和Moho面加载不相关，但均衡时的地表地形和Moho面深度却总体上呈正相关.Moho面越深的地方，地表也越高；Moho面越浅的地方，地表越低.这和我们对于地表起伏和Moho面深度的相关认识是一致的[19］.

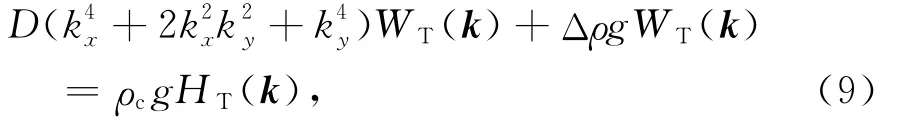
其中kx，ky分别为x，y方向上的波数化简（9）式得到

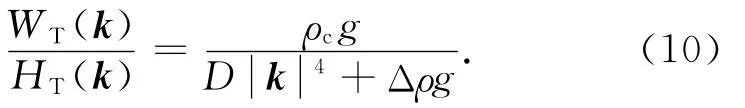
恩哥解答：能，但每天控制咖啡因的摄入量低于 200 毫克，大概 1～2 杯，少放糖，就不会对宝宝造成影响。喝多了，一定程度上会增加流产的风险。

则

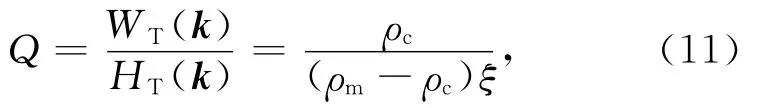
Q即为岩石圈对地表加载的均衡响应函数（线性传递函数，导纳）.

从（11）式可见，只有地表加载时，岩石圈均衡响应函数只是波的函数，与k的方向性无关，且Q为实数.

由政府主导，行业协会指导，跨境电商领军型企业牵头，在共享供应链的基础上，以跨境物流联盟的形式共建海外仓。针对义乌跨境电商产业中跨境物流成本高的问题，一方面通过引导义乌中小跨境电商出口企业在共创品牌提升产品附加值的基础上提高海外仓的应用，加强海外仓物流信息的可视化和透明化，让卖家更好掌控物流、运营、财务等状况；另一方面需要加强规范化建设，主动为企业提供海外仓政策、法律、税收等咨询服务，提供融资、审批、资格认证等政策支持，可通过政府专项资金帮助义乌中小跨境电商出口企业体验海外仓带来的便利和业绩提升，提升义乌小商品的产品附加值和竞争力。

将（1）式代入（11）式便可得到

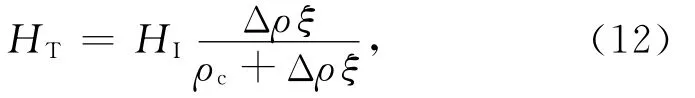
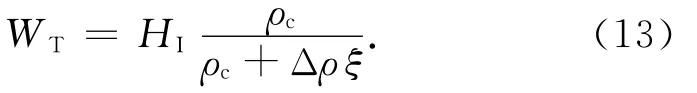
2.2 岩石圈对Moho面加载WI的均衡响应

Forsyth指出，只考虑地表加载，会导致反演的有效弹性厚度远低于真实值.故反演岩石圈弹性厚度时必须考虑地下加载的情况[15］.由于Moho面是岩石圈内密度跳跃最大的密度间断面，并且在地壳内不存在连续的界面[17］，同时，Forsyth指出，只要岩石圈从长波长的均衡补偿到短波长的非均衡补偿的转换波长（一般数百公里）大于重力向下延拓不稳定的波长（一般几十公里）时，将不同深度处的岩石圈内部加载均看作Moho面深度的加载，估计的挠曲强度都是稳健的[15］.因此，我们将岩石圈内部加载简单看作全部由Moho面起伏引起.

如图1（c，d）所示，假定 Moho面深度处存在密度跳跃Δρ，载荷以Moho面深度处地形起伏wi表示：Δρgwi（X）.则在 Moho面载荷Δρgwi（X）的作用下，岩石圈会发生挠曲，在挠曲均衡时，地表起伏为hb，Moho面起伏为wb.则在均衡时的大陆岩石圈的挠曲方程为：

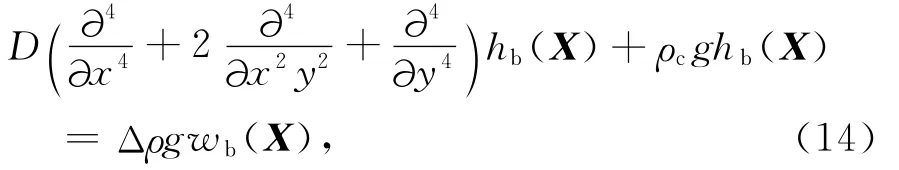
对上式进行傅里叶变换得到

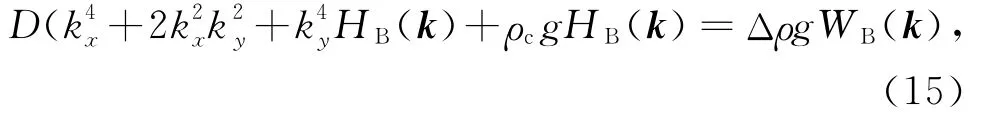
简化式（15）得到

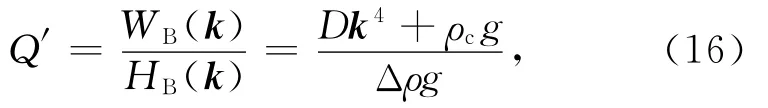
Q′便为只有Moho面加载情况下岩石圈的均衡响应函数（线性传递函数，导纳）.从（16）式可见，类似于Q，只有 Moho面加载时，岩石圈均衡响应函数Q′只是波数的函数，与k的方向性无关.而且Q′为实数.

定义φ=1+Dk4／ρcg.

将（2）带入（16）式，可得

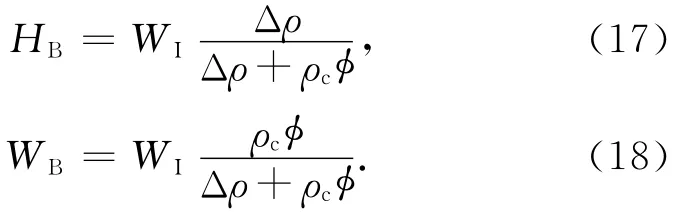
2.3 地表及Moho面同时加载时岩石圈的均衡响应

如图1e所示，岩石圈的地表地形和Moho面起伏是岩石圈对地表及Moho面加载响应的叠加.

将（12），（17）式带入（3），将（13），（18）式带入（4）得到

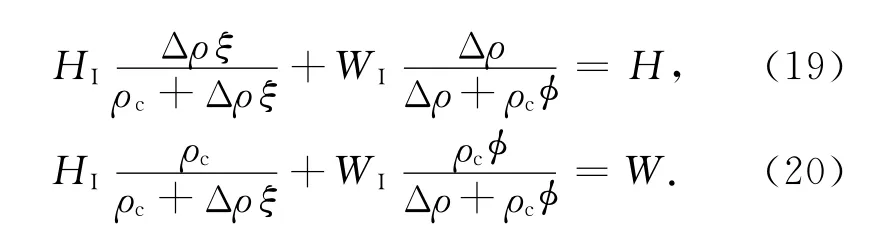
对于给定的有效弹性厚度，便可通过公式（19），（20）由H 和W 得到地表和 Moho面的初始起伏HI，WI，进而确定 HT，WT，HB，WB和

值得注意的是，根据（19），（20）式可同时得到Moho面和地表的载荷比f=ΔρWI／ρcHI.

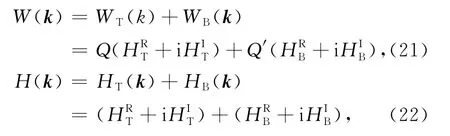
本文首先整体介绍了系统的组成结构和工作原理，然后简要说明了系统的开发平台LabVIEW和相关技术的特点，最后着重分析了在线监测系统的数据传输模块和数据解析处理模块两部分，并展示了最终的网页成果。

武术对外教材内容缺乏标准，影响海外武术习练者的学习效果。武术教学出版物是决定武术国际传播标准化的重要内容。武术国际传播的标准化与武术“走出去”战略的实施息息相关，标准化的传播能够使武术走得更远，而在标准化的传播进程中，武术传播者和传播媒介占据着重要的地位。当下，中国武术协会已出台一系列政策，对赴外武术教师提出相关要求，并且重视赴外武术教师的岗前培训，以期使武术的海外传播道路更加标准化。除此之外，中国武术协会和国际武联应该重点考虑对海外武术教师进行系统培训，让这些教师通过继续教育提升业务素质，从而能够从根本上改善武术海外教材缺乏标准的现状，进一步推动武术国际传播的标准化。

将（21），（22）代入到（6）式，得到

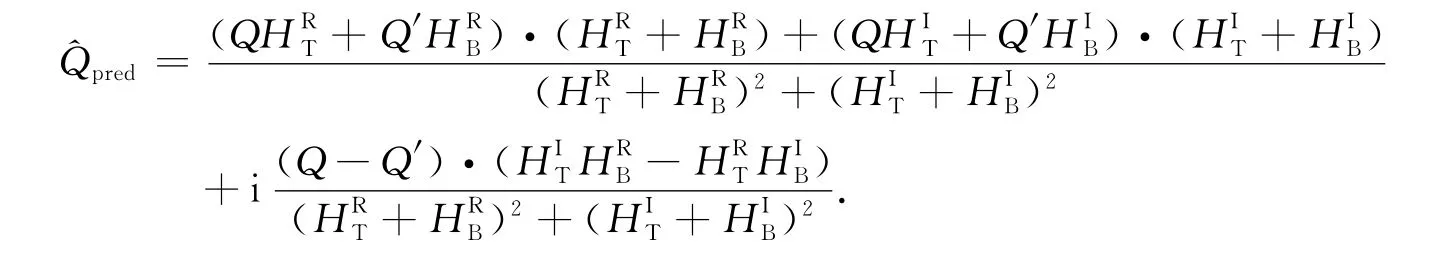
对其进行整理化简得到

为什么，他粗砾带着黑色污垢的手掌拍在我肩上会让我想哭呢，为什么他迷黄浑浊皱纹横生的双眼会让我觉得亲切呢。

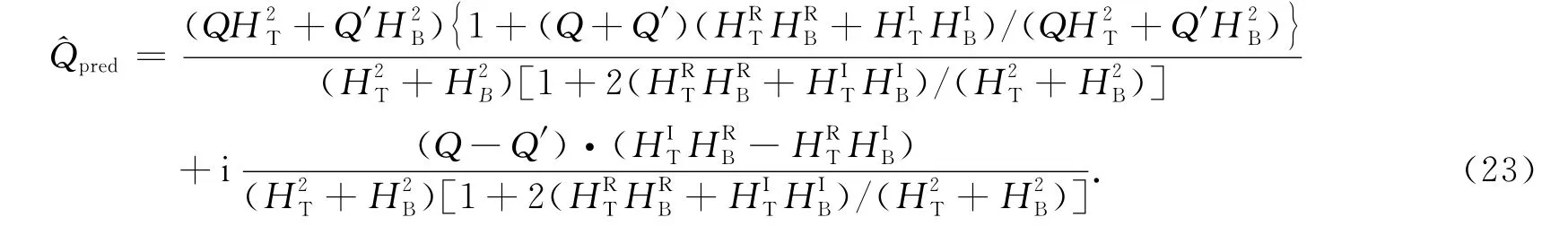
当地表加载和Moho面加载统计不相关时，对一个环形波数带上的功率谱取平均值，则由于以及互不相关且正负相消，将远远小于此时〉的期望应该远小于1.同样的，〉的期望也将远远小于1.故当地表加载和Moho面加载统计不相关时，对一个环形波数带上的功率谱取平均值，一维的理论导纳公式化简为

其中上标R和I分别代表实部和虚部.

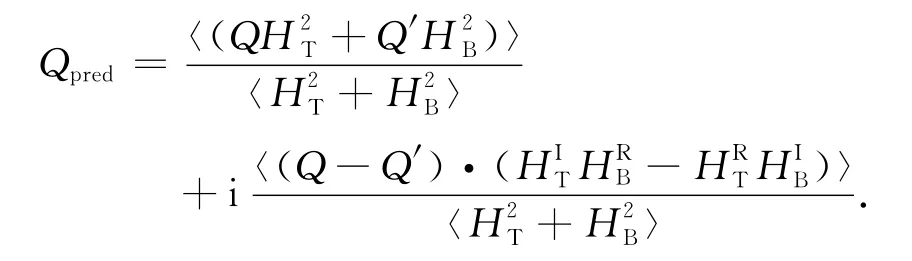
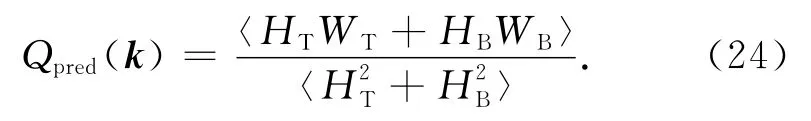
Qpred便为地表和地下加载统计不相关时岩石圈的理论均衡响应函数（线性传递函数，导纳）.

隔了不知道多久，她的手机显示有微信进来。是顾青，问她怎么还没有回家。她没回，然后电话就响了，他们其实很少通电话，为了省钱，总是发微信。她心里觉得，他还是关心她的。她挂掉电话，回了微信，说快到了。

给定地壳和上地幔的密度，如果能够精确地观测到地表地形h（x）和Moho面的起伏w（X），对其进行二维傅氏变换后，对于给定的有效弹性厚度，便可通过公式（19），（20）得到地表和 Moho面的初始起伏 HI，WI，进而确定 HT，WT，HB，WB.根据公式（24），便可确定其一维理论均衡响应函数Qpred.改变有效弹性厚度，便得到不同的均衡响应函数Qpred.选择与观测一维Qobs最接近的理论均衡响应函数所对应的岩石圈有效弹性厚度Te，便为最终反演结果.

即使有多种民意反映渠道，社区居民对于消防安全的知识还是比较匮乏。 笔者随机采访了几个社区居民，发现居民对消防知识只停留在自救层面，比如用湿毛巾捂住口鼻，安全通道的位置等等，但是对于消防器材的具体使用，比如灭火器这类常见器材，却一无所知，这从另一侧面也体现了社区居民的消防安全意识还不够，社区工作人员应该大力宣传消防安全知识，不断丰富居民的自救与灭火知识，增强居民的消防安全意识。

3 利用Moho地形导纳法（MDDF）反演岩石圈有效弹性厚度的模型实验

为了验证本文提出的Moho地形导纳法（MDDF）的可行性和分析其反演精度，这里将在给定的岩石圈有效弹性厚度的基础上，建立随机合成的地表地形和Moho面起伏的数值模型.然后利用该模型数据族，使用Moho地形导纳法（MDDF）反演岩石圈有效弹性厚度，探讨其反演精度，最后将反演结果与Pérez-Gussinyé等利用重力地形导纳的结果[14］进行比较.

3.1 地表地形和Moho面起伏的数值模型

本文合成地表地形和Moho面起伏模型数据的方法类似于Pérez-Gussinyé等的方法[14］.设岩石圈模型（弹性薄板）长宽均为2000km，其有效弹性厚度Te=40km，按照下面的步骤合成地表地形和Moho面起伏：

（1）生成表面随机的初始质量载荷ρcghi（x），其载荷采样点网格间距为25km.在波数域中，初始加载地表地形振幅谱随波数的-2.5次幂关系递减[18］，即

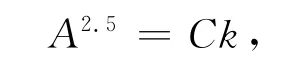
（2）生成随机初始 Moho面质量载荷Δρgwi（X）.为简单起见，地下地表加载比f（k）=ΔρWi（k）／ρcHi（k）的期望不随波数变化，设为E（f（k））=0.5.

模型初始地表起伏和Moho面质量加载分别如图2（a，b）所示.

（3）根据弹性板挠曲公式（公式（19），（20））计算岩石圈达到均衡时的地表地形起伏h和Moho面起伏w作为观测值.

传统的英语教学对于学生的读写能力比较看重，而网络时代背景下，英语教学不仅能够对听、说、读、写能力进行培养，锻炼学生在实际生活中英语的使用能力。多媒体技术下将枯燥乏味的教学内容转化为有趣的视频、动听的音频、丰富的文本，调动了学生的视觉、听觉，激发了学生的学习热情。在使用多媒体进行教学的过程中，应该为学生提供多种的、与教学内容相关要求相符合的教材，激发学生产生积极参与的想法，提高学生对学习的乐趣。此外，相关研究证明让学生快速记住的方法是利用视觉以及听觉，在合适的情景之中代入教学内容，从而在应用和实践过程中增强记忆。

图2还给出了地表载荷（图2a）单独加载下均衡时的地表残余起伏（图2c）和 Moho面起伏（图2d）以及Moho面载荷（图2b）单独加载下的地表起伏（图2e）和Moho面残余起伏（图2f）.

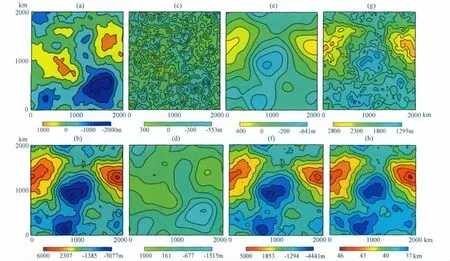
图2 模型加载和岩石圈挠曲（岩石圈有效弹性厚度为40km；为了明确其地质意义，均衡时的地表地形统一加上2km的平均值，Moho面起伏统一加上40km的平均值；地表起伏及地形向上为正，Moho面起伏及深度向下为正）.各图横纵坐标单位为km.图（a），（c），（e），（g）及图（b），（d），（f），（h）分别采用相同的色标.其中，图（g）的2000m对应于图（a）的0m，图（h）的40km对应于图（b）的0km.参见文中详细解释Fig.2 Initial surface and Moho boundary mass loading generated randomly（demonstrated in the form of undulation）（a，b）and the induced surface topography and Moho depth in the isostatic state（g，h）provided that Teis 40km.To compare with observations of topography and Moho interface depth，isostatic topography（g）and Moho depth（h）are added by 2km and 40km，respectively.The units for horizontal and vertical coordinate axes in all subgraphs are all km.（a），（c），（e），（g）have the same color code except that 2000min（g）corresponding to 0min（a）and（b），（d），（f），（h）have the same color code except that 40km in（h）corresponding to 0km in（b）.See text for details

3.2 利用合成数值模型反演岩石圈有效弹性厚度实验

计算Moho地形导纳时，需要求取地表地形的自功率谱密度与Moho起伏与地表地形的互功率谱密度.本文使用Multitaper方法对功率谱密度进行估计.Multitaper谱估计方法能够有效降低频谱泄漏，而且在数据量少的情况下，仍然能够较精确地确定功率谱密度[20］.Hanssen将Multitaper方法推广到了多维的情况[21］.本文使用Hanssen提出的方法进行二维功率谱的估计.

假定岩石圈在某一垂向力的加载下产生挠曲.观测到的数据为地表地形起伏和Moho面起伏.我们可以根据下面的方法得到该岩石圈有效弹性厚度随空间的变化：选取某一个滑动窗口，根据该窗口的地形和Moho面起伏观测值推测其平均有效弹性厚度，作为窗口中央的有效弹性厚度.移动该窗口，便可以获得有效弹性厚度随空间的变化情况.

为了得到有效弹性厚度反演结果的统计特性，我们选取大小为1000km×1000km的滑动窗口，并以100km为间隔移动窗口以得到有效弹性厚度随空间的变化图.理论上，由于每一点的有效弹性厚度都是常数40km，每个窗口反演得到的有效弹性厚度应当都等于真实值40km.但由于实际反演过程存在偏差，会导致有效弹性厚度的估计值偏离真实值.对所有窗口反演的有效弹性厚度取平均值及均方差，与前人结果进行比较，可以验证本方法的可行性.

3.3 岩石圈有效弹性厚度的反演结果分析

图3为有效弹性厚度选取不同的数值时某一随机选取窗口的理论导纳对观测导纳的拟合图.从拟合结果图可以看到，当Te在40～70km之间时，理论导纳对观测导纳拟合的比较好（最优值为Te=46km）.

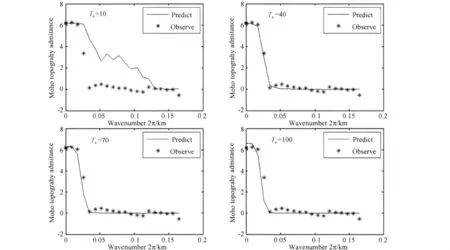
图3 某一随机选取的1000km×1000km的窗口，不同有效弹性厚度理论导纳与观测导纳拟合图.对此窗口，当Te=46km时，理论导纳与观测导纳拟合最好Fig.3 Fitting observed admittance curve using predicted admittance curves with different Teof a random chosen window with 1000km×1000km size.Predicted admittance fits observed admittance best when Te=46km for this window

图4 和图5分别为1000km×1000km滑动窗口反演的岩石圈有效弹性厚度的伪彩图和直方图.从图中可见所有有效弹性厚度的拟合结果均大于20km小于50km.反演结果的均值为33.3km，均方差为5.8km，这要优于Pérez-Gussinyé等对于相同大小滑动窗口的反演结果[14］：平均值50km，均方差21.5km.证实了使用本方法可以获得较高精度的有效弹性厚度.

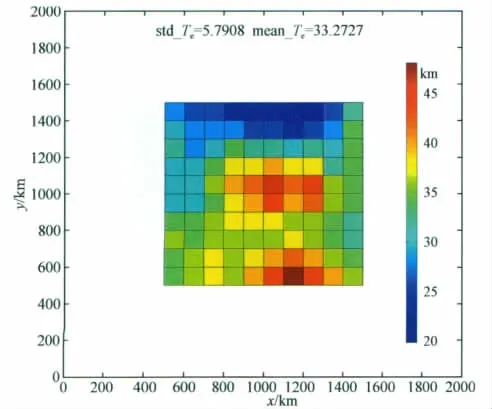
图4 各个窗口反演的岩石圈有效弹性厚度的伪彩图.mean＿Te，std＿Te分别为弹性厚度反演结果的均值及均方差.图中外方框为数据区域，内方框为反演区域Fig.4 Pseudo-color pictures of inversed elastic thickness for each window.mean＿Teand std＿Tein the title line represent average value and standard deviation of inversed elastic thickness，respectively.Outer box stands for the margin of data area

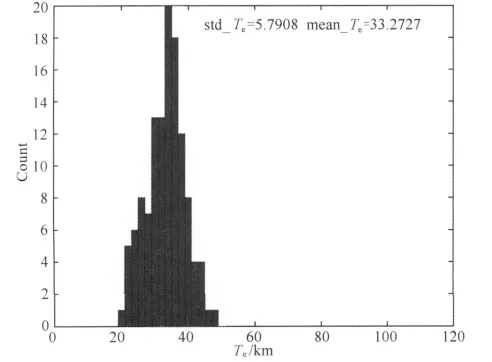
图5 窗口反演的岩石圈有效弹性厚度直方图Fig.5 Histogram of inversed elastic thickness

从上面模型的建立过程可以看出，本文给出的反演有效弹性厚度模型的准确性主要受到两个方面的制约：（1）数值模型建立的本身，即在给定有效弹性厚度Te和岩石弹性常数的基础上，由随机模型给定的 H，W 得到 HT，WT，HB，WB；（2）由 HT，WT，HB，WB得到＾Qpred.如果这两个步骤结果精确，我们便能够比较精确地确定岩石圈有效弹性厚度.不考虑计算误差，如果方程组（19）（20）非奇异，则解得的HT，WT，HB，WB就是准确的.方程组（19），（20）非奇异的条件是ξφ≠1（无限长波长或岩石圈有效弹性厚度等于零，岩石圈处于Airy均衡状态时，ξφ=1，方程组奇异）.本文使用的窗口均为有效大小窗口，因此上述条件（1）满足.从公式（25）简化为公式（26）的前提是环形波数带上，上下交叉项的均值的期望为0.因此，同一环带上的数据越多，其平均值接近于零的概率越大.所得结果方差将越小.增加同一环带上数据量的方法有两个：增加窗口大小，减小采样间隔.因此，适当地增加窗口大小或减小采样间隔，应该会得到更高精度的反演结果，而有效弹性厚度的反演均值应该在真值附近浮动.数值实验表明，在模型有效弹性厚度保持40km不变的前提下，增大滑动窗口或减小采样间隔，都能减小反演均方差.不同采样间隔和滑动窗口的数值模型反演的结果见表2.

Pérez-Gussinyé等2004年的文章中使用的采样点间距为8km[14］，远小于本文，但其精度低于本文.这更加表明使用Moho面起伏代替重力异常数据反演有效弹性厚度能够较好地提高反演精度（见表2）.

青樱当众受辱，心中暗自生怒，只硬生生忍着不做声。惢心已经变了脸色，正要上前说话，青樱暗暗拦住，看了跟在身后的格格苏绿筠一眼，慢慢跪了下去。

用无菌接种环挑取纯化后的菌株至装有100 mL已灭菌的2216E液体培养基的三角瓶锥形中，低温振荡培养 3 d(10 ℃，120 r/min)形成降解菌母液。

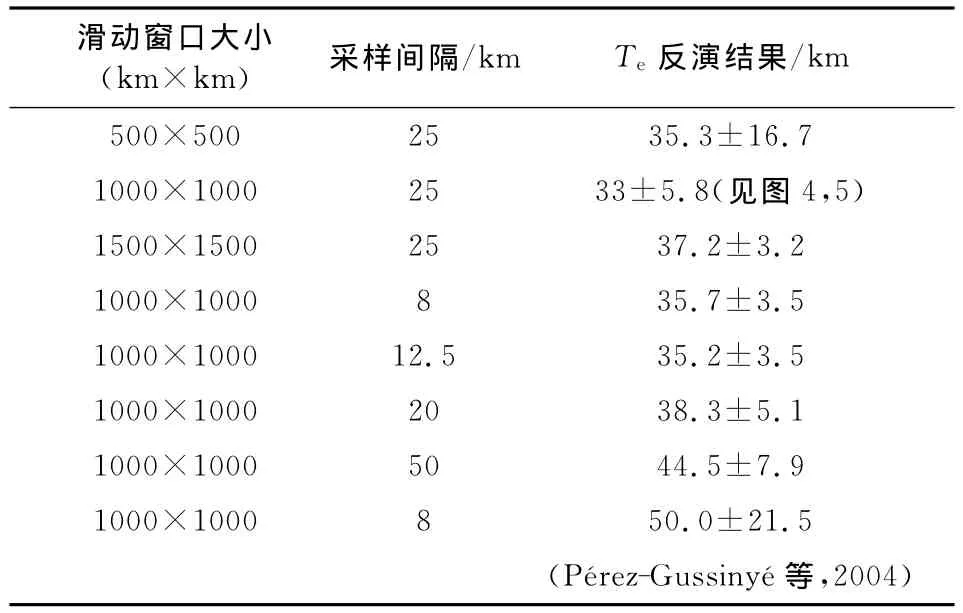
表2 不同大小反演窗口及采样间隔下有效弹性厚度的反演结果 最后一行为Pérez-Gussinyé等的反演结果[14］Table 2 Inversed Tewith windows of different tapering size and different sampling spaces.The last line is inversed results by Pérez-Gussinyéet al[14］

4 结论和讨论

本文提出了反演岩石圈等效弹性厚度的Moho地形导纳法（MDDF），并利用合成数值模型反演了岩石圈等效弹性厚度.数值模型反演的实验结果表明：

2017年8月8日，共建“平安西江”行动启动。记者通过专访广东海事局局长陈毕伍了解到，在一年多的建设时间里，共建“平安西江”行动取得了阶段性成果，该行动也让广东海事局追求的水上安全监管长治久安目标得到进一步实现。

（1）Moho地形导纳法（MDDF）使用 Moho面起伏数据代替重力数据能够实现对岩石圈有效弹性厚度的反演，明显提高其反演精度.

（2）有效弹性厚度的反演精度受到采样点数的影响.因此，采样点越密集，反演精度越高；滑动窗口越大，反演精度越高.

本文提出的有效弹性厚度的Moho地形导纳法（MDDF）反演精度较传统的重力导纳法高[14］，一个可能的原因是文献[14］在由模型Moho面起伏生成重力异常时损失了精度.不过我们的数值模型实验否定了这一可能性.实验中使用与文献[14］相同的方法产生了重力异常，并利用生成的重力异常和地表地形反演了Moho面起伏，再由反演的Moho面起伏联合地表地形反演有效弹性厚度，其精度接近本文直接使用Moho面的反演精度，仍高于Pérez-Gussinyé等方法的结果.这说明，使用本文的Moho地形导纳法（MDDF）确实能提高反演精度，实验结果将另文阐述.

本文的模型隐含地壳和岩石圈地幔部分在挠曲时耦合在一起.然而，并非在任何地区，这一耦合的模型都成立.弱耦合和解耦的情况也是存在的.所以在实际应用中，必需估计弱耦合和解耦对于反演结果和精度的影响.另外，本文数值模型中假定岩石圈所受内部载荷均来自Moho面的起伏，而在实际应用中，壳内热分布不均匀性，地幔力学作用产生的底辟和岩浆等都会使岩石圈产生挠曲，这将在一定程度上影响反演结果和降低本文方法的反演精度.第三，从模型结果分析可知，岩石圈软流圈分界面（LAB）的起伏等同于岩石圈的挠曲.然而，考虑到岩石圈和软流圈界面LAB对水含量，组分等都非常敏感[22-23］，故LAB界面将远比实验模型复杂得多.不过，由于LAB不是个密度界面，其起伏的变化估计不会对岩石圈的挠曲产生大的影响.

致 谢 直接使用Moho面反演有效弹性厚度的思路最初是在与倪四道教授交流后产生的，两位外审专家为作者提供了宝贵的意见，在此一并表示感谢.

（References）

[1]Burov E B，Diament M.The effective elastic thickness（Te）of continental lithosphere：What does it really mean？J.Geophys.Res.，1995，100（B3）：3905-3927.

[2]熊熊，许厚泽，徐建桥等.大陆弹性岩石层有效弹性厚度对岩石层形变和大地水准面的动力影响.地壳形变与地震，1998，18（4）：1-10.Xiong X，Xu H Z，Xu J Q，et al.Dynamic influence of various elastic thickness of continental lithosphere upon lithospheric deformation and geoid undulation.Crustal Deformation and Earthquake （in Chinese），1998，18（4）：1-10.

[3]Pérez-Gussinyé M，Watts A B.The long-term strength of Europe and its implications for plate-forming processes.Nature，2005，436（7049）：381-384.

[4]付永涛，李继亮，周辉等.大陆岩石圈有效弹性厚度研究综述.地质评论，2000，46（2）：149-159.Fu Y T，Li J L，Zhou H，et al.Comments on the effective elastic thickness of continental lithosphere.Geological Review （in Chinese），2000，46（2）：149-159.

[5]Dorman L M，Lewis B T R.Experimental isostasy 1.Theory of the determination of the Earth′s isostatic response to a concentrated load.Journal of Geophysical Research，1970，75（17）：3357-3365.

[6]Watts A B.The effective elastic thickness of the lithosphere and the evolution of foreland basins.Basin Research，1992，4（3-4）：169-178.

[7]Jordan T A，Watts A B.Gravity anomalies，flexure and the elastic thickness structure of the India-Eurasia collisional system.Earth and Planetary Science Letters，2005，236（3-4）：732-750.

[8]Karner G D，Watts A B.Gravity anomalies and flexure of the lithosphere at mountain ranges.Journal of Geophysical Research，1983，88（B12）：10449-10477.

[9]McKenzie D，Fairhead D.Estimates of the effective elastic thickness of the continental lithosphere from Bouguer and free air gravity anomalies.Journal of Geophysical Research，1997，102（B12）：27523-27552.

[10]Anderson F S，Smrekar S E.Global mapping of crustal and lithospheric thickness on Venus.Journal of Geophysical Research，2006，111（E8）：E08006.

[11]李斐，柯宝贵，王文睿.利用重力地形导纳估计月壳厚度.地球物理学报，2009，52（8）：2001-2007.Li F，Ke B G，Wang W R.Estimation of the ancient lunar crust thickness from the admittance.Chinese Journal of Geophysics （in Chinese），2009，52（8）：2001-2007.

[12]Watts A B，Burov E B.Lithospheric strength and its relationship to the elastic and seismogenic layer thickness.Earth and Planetary Science Letters，2003，213（1-2）：113-131.

[13]Maggi A，Jackson J，McKenzie D，et al.Earthquake focal depths，effective elastic thickness，and the strength of the continental lithosphere.Geology，2000，28（6）：495.

[14]Pérez-GussinyéM，Lowry A R，Watts A B，et al.On the recovery of effective elastic thickness using spectral methods：examples from synthetic data and from the Fennoscandian Shield.J.Geophys.Res.，2004，109：B10409.

[15]Forsyth D W.Subsurface loading and estimates of the flexural rigidity of continental lithosphere.Journal of Geophysical Research，1985，90（B14）：12623-12632.

[16]Turcotte D L，Schubert G.Geodynamics.Cambridge：Cambridge University Press，2002.

[17]曾融生，孙为国，毛桐恩等.中国大陆莫霍界面深度图.地震学报，1995，17（3）：322-327.Zeng R S，Sun W G，Mao T E，et al.Map of the depth of Moho of China.Acta Seismologic Sinica（in Chinese），1995，17（3）：322-327.

[18]Mandelbrot B B.The Fractal Geometry of Nature.New York：W.H.Freeman，1983.

[19]黄建平，傅容珊，许萍等.利用重力和地形观测反演中国及邻区地壳厚度.地震学报，2006，28（3）：250-258.Huang J P，Fu R S，Xu P，et al.Inversion of gravity and topography data for the crust thickness of china and its adjacency.Acta Seismologica Sinica （in Chinese），2006，28（3）：250-258.

[20]Thomson D J.Spectrum estimation and harmonic analysis.Proceedings of the IEEE，1982，70（9）：1055-1096.

[21]Hanssen A.Multidimensional multitaper spectral estimation.Signal Processing，1997，58（3）：327-332.

[22]Karato S I，Jung H.Water，partial melting and the origin of the seismic low velocity and high attenuation zone in the upper mantle.Earth and Planetary Science Letters，1998，157（3-4）：193-207.

[23]Green D H，Hibberson W O，Kovács I，et al.Water and its influence on the lithosphere-asthenosphere boundary.Nature，2010，467（7314）：448-451.