Ti62421s钛合金的热变形行为及加工图

戚延龄，夏长清，王志辉，王玲，李学雄，孙玮

(中南大学 材料科学与工程学院，湖南 长沙，410083)

热加工是制造金属材料零部件的重要加工工序，采用热加工不仅可以获得所需要的形状，而且可以通过加工及热处理调控材料的微观组织，从而提高材料的综合力学性能。钛合金热处理不能达到细晶强化的目的，只有通过变形才能实现细晶强化。Ti62421s钛合金是由宝钛集团自行研究设计的新型近α钛合金，该合金具有密度小、比强度高、耐高温、耐腐蚀和疲劳性能好等优良特性。其相组成为大量的密排六方(hcp)结构的α相和少量的体心立方(bcc)结构的β相，在室温下很难进行塑性变形，所以热加工在该类型合金中对改善合金的组织和提高性能有着非常重要的意义。随着计算机科学与技术的发展，数值模拟技术在材料加工性能研究中的应用越来越广泛，利用数值模拟可以在计算机上再现材料加工全过程，通过对计算机采集到的热加工性能数据进行分析，可研究其热变形行为[1-6]。加工图(Processing map)是 Prasad等基于动态材料模型(DMM)理论发展的一种分析材料热变形行为的新方法。加工图是变形温度与应变速率空间中的功率耗散图与失稳图的叠加，根据加工图可以判断材料变形过程中的流变失稳区，还可根据非失稳区内最大功率耗散系数区与显微组织来制定材料的最佳加工工艺。用加工图来分析和预测在热加工过程中的不稳定性[7]，以及用加工图作为设计很多近净成形(Near net shape)材料热加工工序的依据[8-11]，其在钛合金加工中的越来越普遍[12-13]。本文作者研究Ti62421s合金在高温下的真应力-真应变关系曲线，并通过对其变形过程中的参数(如变形温度和变形速率)以及热模拟数据(如峰值应力)的研究分析获得合金的动力学参数(应力敏感系数和变形激活能)，而且采用基于动态材料模型(Dynamic material modeling)建立Ti62421s在应变量为60%的加工图，以便为Ti62421s合金的热加工工艺优化的提供理论和实验依据。

1 实验材料和方法

实验所用材料为Ti62421s钛合金，属Ti-Al-Sn-Zr-Mo-Nb系近α钛合金，由宝钛集团提供，其相变点温度为 1 000 ℃[14]，采用线切割的方法将试样加工成直径×高为8 mm×12 mm的圆柱体。

Ti62421s合金热压缩实验在Gleeble-1500热模拟实验机上进行，应变速率选择为0.001～10 s-1，变形温度为900～1 060 ℃，变形量为60%。试样以10 ℃/s的加热速率加热到变形温度保温5 min后进行热压缩变形，试验完后立即水淬以保留高温变形组织。变形过程中由计算机自动采集载荷、位移、温度和时间等实验数据。

2 实验结果与讨论

2.1 Ti62421s合金高温压缩的真应力-真应变曲线

根据采集到的载荷与位移数据，通过换算获得合金的真应力-真应变曲线图，图1所示为Ti62421s合金在不同温度(900，940，980，1 020和1 060 ℃)和不同应变速率(0.001，0.01，0.1，1和10 s-1)下的真应力-真应变曲线。

从Ti62421s合金的真应力-真应变曲线图可以得出以下基本特征。

(1) 在本实验参数范围内，Ti62421s合金的流变应力随着变形温度的升高而降低，随着应变速率的升高而升高。

(2) Ti62421s合金在高温下(900～1 060 ℃)进行压缩变形时，在变形初始阶段，随着应变量的增加，位错增殖，产生加工硬化，提高合金的变形抗力，由于未发生动态再结晶，其真应力随真应变增加而迅速增加，很快升至峰值，真应力-真应变曲线呈直线上升，其斜率很大；而且随着应变速率的增加，加工硬化更明显，曲线斜率增大。在变形过程中加工硬化导致材料更容易发生动态回复和动态再结晶。

(3) 在本实验参数范围内，随着变形温度和应变速率的变化，Ti62421s合金变形过程中真应力达到峰值时真应变不同。合金在900～940 ℃温度范围内经不同应变速率(0.001～10 s-1)变形时，合金的真应变约为0.02～0.10，随着变形温度的升高或应变速率的下降，达到峰值应力时真应变逐渐减小；当合金在 980～1 060 ℃经不同应变速率变形时，合金的真应变为0.01～0.02。从而可以看出：随着温度的升高，合金达到应力峰时真应变明显减小，而且达到峰值应力的真应变之间的差值随着温度的升高而减小，说明随着变形温度的升高，流变应力对变形温度的敏感性降低。该合金属于应变速率敏感型和热敏感型材料。

(4) 在本实验参数范围内，随着变形温度的升高，对应的峰值应力逐步减小。随着变形温度的升高，材料内能增加，金属原子的扩散能力提高，有利于动态回复或动态再结晶的发生，从而降低了合金的加工硬化程度，使得合金的峰值应力减小。

(5) 在本实验实验温度范围内，应变速率对真应力-真应变曲线的形态有较大影响。在高应变速率(10 s-1)和变形温度高于 980 ℃(包括 980 ℃)时,合金的真应力-真应变曲线出现 1个明显应力峰值，随后应力急剧下降或者出现明显的上下屈服点，即应力出现不连续屈服现象。材料压缩变形过程中温度越高，应变速率越高，这种应力不连续屈服现象越明显。周军等[15-16]在研究Ti-3Al-5V-5Mo合金时也发现了类似现象，他们认为材料内部组织可能发生动态再结晶、动态时效或者局部流变。这种不连续屈服现象最早在bcc的材料低温变形时发现，在β钛合金高温变形时也发现了类似现象[17-23]。

(6) 随着压缩变形继续进行，在变形过程中发生动态回复和动态再结晶，从而引起合金中位错密度下降，造成合金的软化。但由于变形还在继续，加工硬化和动态回复与动态再结晶的软化交替作用导致合金真应力曲线逐步下降或趋于动态平衡。变形温度越高或应变速率越低，该现象越明显。

图1 Ti62421s合金在不同变形温度和应变速率下的真应力-真应变曲线Fig.1 True stress-strain curves of Ti62421s alloy at different deformation temperatures

2.2 Ti62421s合金热变形参数对其显微组织的影响

2.2.1 热变形参数对Ti62421s合金显微组织的影响

图2 合金在900 ℃不同应变速率的组织形貌金相照片Fig.2 Microstructure of Ti62421s alloy at 900 ℃ at different strain rates

研究应变速率为0.001，0.01，0.1，1和10 s-1对显微组织的影响。图2所示为变形温度为900 ℃时，合金经不同应变速率变形后立即水淬所获得的显微组织。从图2可看出：当合金在900 ℃变形时，随着应变速率的变化，合金显微组织发生明显变化；当应变速率为10 s-1时，由于变形作用，合金原始组织都呈现出明显的取向性。条状的α相沿与压缩方向垂直的方向被拉长；当被压缩的晶粒压缩受阻时则发生弯曲或扭折，如图2(c)所示；当应变速率为0.1～1 s-1时，由于变形速率较慢，材料发生动态再结晶及长大，但由于在该温度的停留时间不够长，所以，晶粒再结晶长大不够明显，如图2(b)和(c)所示；随着应变速率的进一步下降，当应变速率为0.001 s-1时，在该温度下的停留时间足够长，从而再结晶形成α相有足够的时间长大，所以，此时的再结晶及长大现象比应变速率为0.1 s-1时更加明显。而且变形时间足够长也使得动态回复与动态再结晶及长大现象能够充分进行，形成大量等轴的α相，如图2(a)所示。

2.2.2 变形温度对Ti62421s合金显微组织的影响

图3所示为合金在不同温度和1 s-1应变速率下变形立即水淬后的组织形貌金相照片。从图3可以看出：当应变速率为1 s-1时，随着变形温度的升高，合金显微组织发生明显变化。当合金变形温度在 θ(α+β)/β相变温度以下900 ℃变形时，原始棒状α相被明显拉长、弯曲和扭折，造成原始组织的破碎，并有球化趋势，如图3(a)所示。当变形温度升高到980 ℃时，由于此时的温度接近相变温度，大量α相转变成β相，少量α相在变形过程中发生球化。由于此时温度相对较低，且变形速率较快，合金中α相稳定元素的扩散不均匀，导致变形后的试样立即水淬后只有少量的马氏体组织生成。

当合金在 θ(α+β)/β相变温度以上变形时，显微组织为粗大的β晶粒内析出针状α′，即β相在水淬过程中发生马氏体转变，且变形温度越高，水淬生成的针状α′相(马氏体相)越明显，且尺寸越大。在相变温度以上变形时高温β相晶粒非常粗大，并且沿垂直压缩方向被明显拉长，如图3(c)和(d)所示。当合金的变形温度超过 θ(α+β)/β转变温度后，由于温度的升高，合金元素扩散越容易，其中α稳定元素扩散更容易，更加均匀地分布在基体中，在变形后水淬过程中发生马氏体相转变的区域越多。变形温度越高合金元素分布越均匀，马氏体相转变现象越明显。

2.3 Ti62421s合金流变应力模型的建立

在金属材料的高温压缩变形过程中，流变应力是影响材料成型过程中非常重要的因素，它与材料变形时的应变速率ε˙，变形温度θ和应变ε之间存在一定的函数关系[24]：

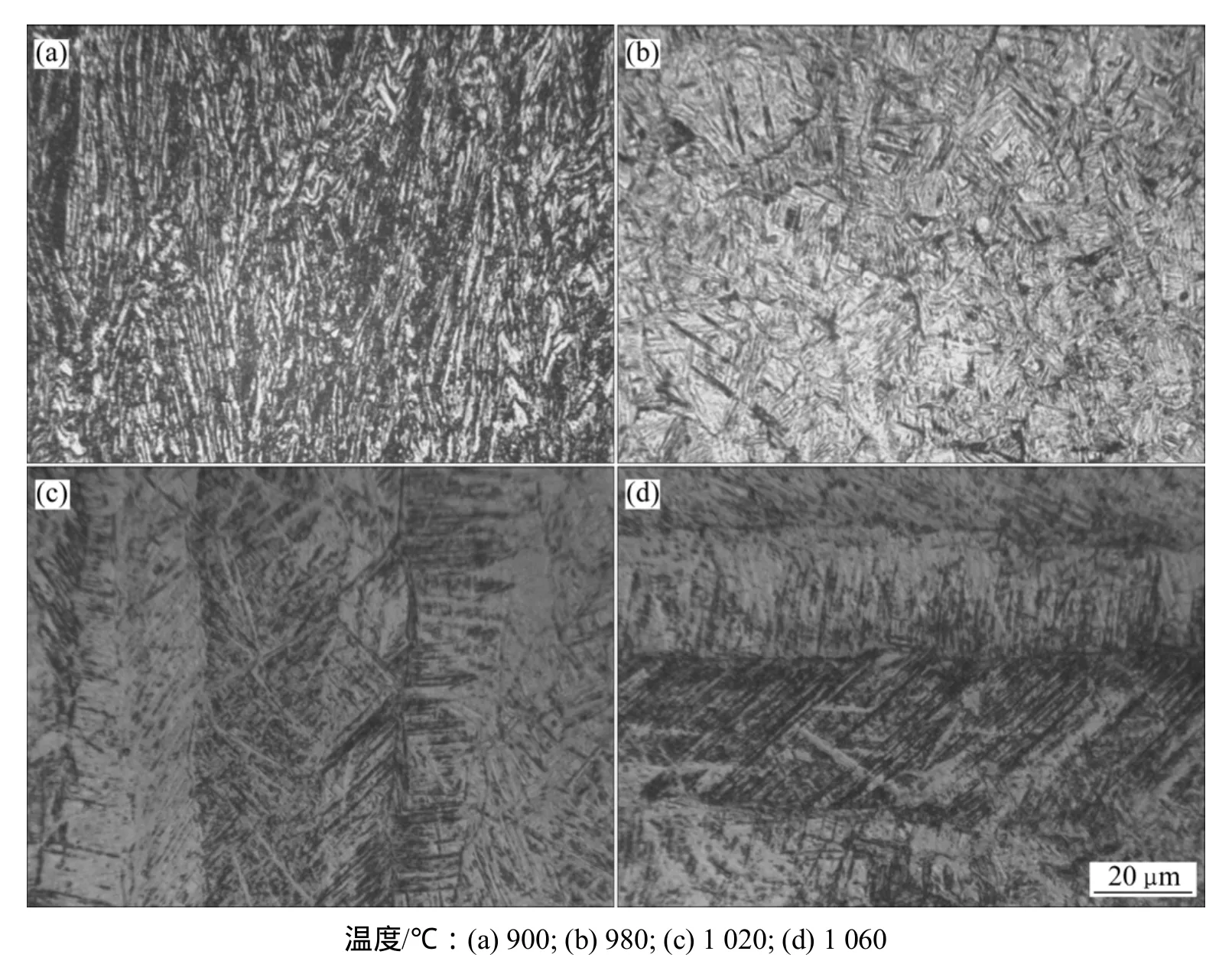
图3 合金在不同温度下1 s-1应变速率的组织形貌金相照片Fig.3 Microstructure of Ti62421s alloy at 1 s-1 strain rate at different temperatures

在低应力水平下(ασ＜0.8)，

在高应力水平下(ασ＞1.2)，

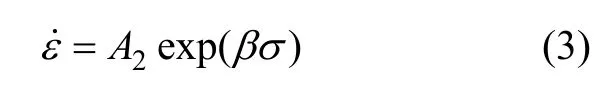
式中：A1，A2，n和 β为与温度无关的材料常数；Q为变形激活能，kJ/mol；R为气体常数；ε˙为应变速率，s-1；T为热力学温度，K。

式(2)和式(3)描述了热变形过程中应变硬化(加工硬化)和动态软化过程之间的动态平衡，与稳态蠕变变形对应的关系[24]非常相似，高温变形受热激活控制。Sellars和Tegart综合了式(2)和式(3)提出一种包含变形激活能Q和温度T的双曲正弦形式的本构模型[25～27]，采用一个含应力σ的双曲正弦形式修正 Arrhenius关系来描述这种热激活行为。

式中：A为与温度无关的材料常数；n1为材料硬化指数，n1=β/α。

对式(2)和式(3)分别取对数，可得

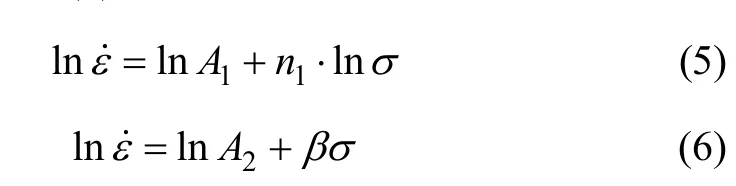
热加工变形，如挤压和压缩等，视为在大应变速率和高应力水平下蠕变的一种外延，可由式(4)很好地拟合。本实验中合金的高温压缩变形，其稳态流变(峰值)应力σ与ε˙和T的关系亦服从式(4)。

1944年Zener和Hollomon[28-29]在研究钢的应力-应变关系时发现它取决于温度T和应变速率ε˙，而T和ε˙的关系可以用一个参数Z来表示：

式中：Z为Zeneer-Hollomon参数，其物理意义是温度补偿的变形速率因子；Q是变形激活能，它反映材料热变形的难易程度，也是材料在热变形过程中重要的力学性能参数，其值通常和激活焓ΔH相等。Z与σ之间服从以下关系式：

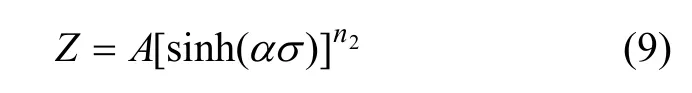
结合式(8)和式(9)可得：

式中：A，α，n2和Q均为材料常数。

在研究材料热变形行为时，通常应先了解与应变速率和温度有关的流变应力规律，从式(10)可推导出：

对式(11)两边取自然对数，可得：

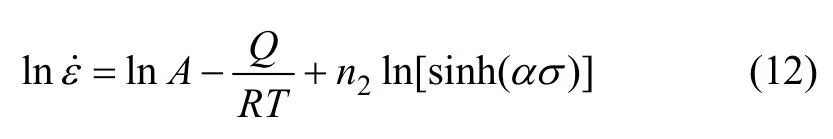
将试验结果依据式(12)在 Origin软件中画出ln ε˙- ln[sinh(ασ)]和 ln[sinh(ασ) ]- 1/T的关系图，并对其数据进行线性拟合，拟合后结果如图4(c)和(d)所示 。 从 图 4可 以 看 出 ： ln ε˙- ln[sinh(ασ)]和ln[sinh(ασ) ]- 1/T 关系曲线都近似呈直线关系。通过图 4(c)拟合 ln ε˙- ln[sinh(ασ)]关系后的斜率取其倒数并求出其平均值，得出 n2=3.39。通过图 4(d)拟合ln[sinh(ασ) ]- 1/T 关系后的斜率B=14 791.86 (其中，B=Q/(Rn2)，即 Q=Rn2B)。

由式(12)可知：拟合后 ln[sinh(ασ) ]- 1/T 关系后的斜率 B= Q/( Rn2)，所以，Ti62421s合金的激活能Q=Rn2B=416.418 32 kJ/mol。

根据双曲线正弦函数的定义，应有：

由此可以将流变应力σ表述为Zener-Hollomon参数Z的函数：

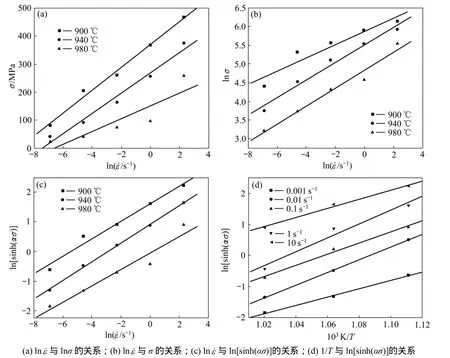
图4 Ti62421s合金高温塑性变形峰值应力σ与应变速率ε˙和变形温度T的相关性Fig.4 Relevance of high temperature plastic deformation peak stress σ and strain rate ε and deformation temperature T of Ti62421s alloy

因此，由Ti62421s合金峰值应力求出合金的高温压缩本构方程的材料常数见表1。

表1 Ti62421s合金峰值应力本构方程的材料常数Table 1 Material constants of Ti62421s alloy peak stress of constitutive equation

将表 1中的材料常数代入式(4)和式(14)，得到Ti62421s合金高温流动应力本构方程：

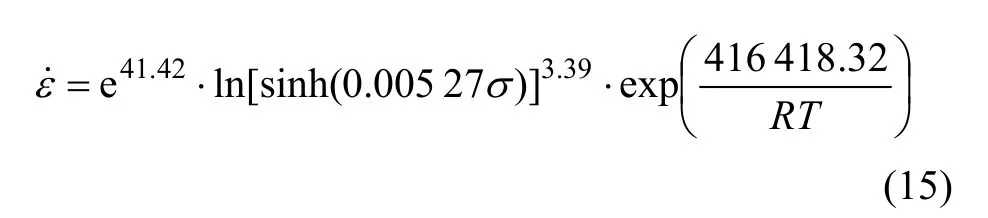
其Z参数可表示为：

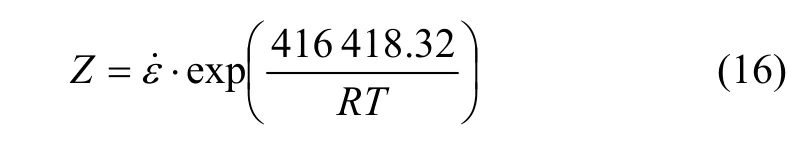
流变应力方程也可以用Z参数表述为：

2.4 Ti62421s合金加工图的建立

2.4.1 基于动态材料学模型的热加工图理论

动态材料模型(DMM)是基于大塑性变形的连续介质力学、物理系统模拟和不可逆动力学等方面的基本原理建立起来的。该模型的基本原理为：假设将热变形的加工件作为一个能量耗散体，在塑性变形过程中，将外界输入加工件的总能量(P)消耗在以下2方面：

(1) 加工件发生塑性变形所消耗的能量，用G表示；

(2) 加工件变形过程中组织变化而耗散的能量，用J表示。

这一过程可以通过数学表达式体现：

为了保证应变速率敏感因子m的精度，一般采用三次样条函数拟合流变应力lnσ与 ε˙ ln 的函数关系，即：

式中：k1，k2，k3和k4为拟合系数。

这2种能量所占比例由加工件在一定应力下的应变速率敏感指数m决定：

所以，对式(20)式两边同时微分，即：

耗散协量J的微分可表示为：

则J可表示为：

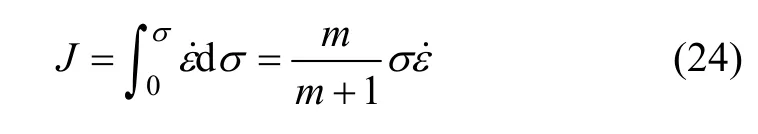
式中：m的取值范围为0～1，当m=1时，材料处于理想性耗散状态，耗散协量J达到最大值，即：

在这里引进一个反应材料功率耗散特征的无量纲参数 η为功率耗散效率(Efficiency of power dissipation)，其值为：

参数η描述了在试验温度和应变范围内材料变形过程中的不同微观机制的本质反应。η是随着应变速率和试验温度的变化而变化，而且功率耗散效率与材料微观组织有紧密联系。在应变一定的条件下，作温度T和应变速率ε˙与功率耗散效率η的关系图，就可以得到功率耗散图。

将不可逆热动力学的极大值理论应用于大应变塑性流变中，当 dD /dε ˙＜ D /ε˙时，会出现流变失稳，式中D是在给定温度下的耗散函数。按照动态材料模型原理，D等于协变量 J，由上述分析可得到流变失稳的判据为[30]：

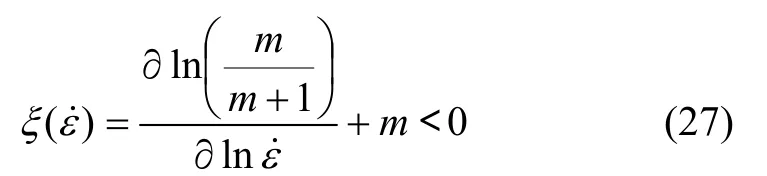
参数ξ()ε˙作为变形温度和应变率的函数，在能耗图上该值为负的区域称为流变失稳区域，该图称为流变失稳图。上述流变失稳判据具有特定的物理意义，如果系统不能以施加在系统上的应变率以上的速率产生熵，那么，系统就会产生局部流变或者形成流变失稳。流变失稳的微观现象是形成绝热剪切带，发生局部变形、动态应变失效、机械孪晶和扭折。

根据式(19)，(29)和(21)可得到：

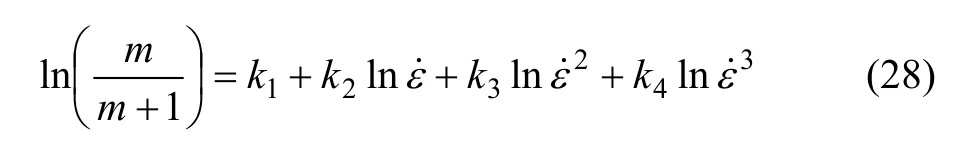
式中：k1，k2，k3和k4为拟合系数。

材料的加工性能不仅与功率耗散效率有关，还与材料加工失稳有关。因为在功率耗散图中，功率耗散效率η大的区域有可能ξ(ε˙)小于0(材料处于失稳区)。将功率耗散图与失稳图结合就可以得到材料的加工图。

2.4.2 Ti62421s合金的热加工图绘制

通过高温压缩实验采集合金在不同应变、应变速率和变形温度下的流变应力值，进而作出不同应变量的加工图。加工图绘制过程如下。

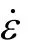
(2) 利用 Matlab求出式(20)中三次样条函数的 4个系数k值；

(3) 利用上面求解的系数 k，代入式(22)，求出m值；

(4) 根据式(24)求解功率耗散效率 η，然后作图“n-lnε˙- T ”，即为 Ti62421s合金的功率耗散图，如图5所示。

(5) 利用Matlab求解三次样条函数：

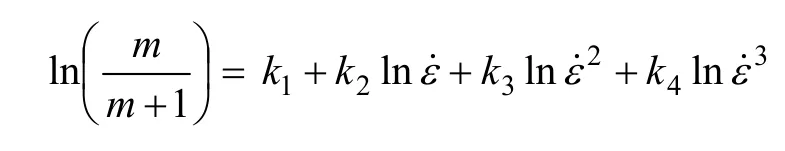
的4个系数，将求出的系数代入式(29)，求出ξ(ε˙)，然后作图“ n-lnε˙- T ”，即为 Ti62421s合金的失稳图，如图6所示。

图5 Ti62421s合金的功率耗散图Fig.5 Power dissipation map of Ti62421s alloy

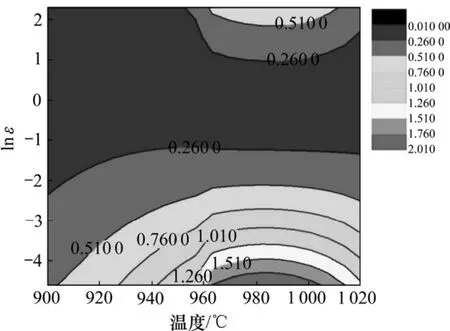
图6 Ti62421s合金的失稳图Fig.6 Instability map of Ti62421s alloy

(6) 将失稳图中ξ(ε˙)＜0的区域与功率耗散图组合就能得到加工图。在实验条件(应变速率 0.01～10 s-1，温度900～1 020 ℃)范围内，没有ξ()ε˙＜0区域，但戚运莲[4]认为功率耗散效率η小于30%的区域通常为失稳区。本研究将功率耗散效率η小于30%的区域定为失稳区，获得 Ti62421s合金的加工图，如图 7所示。

2.4.3 功率耗散效率分析

从图7所示的Ti62421s合金加工图上可以看出：功率耗散效率η受变形温度和变形速率的影响很大，不同区域的η相差较大。变形速率越慢，η越大；随着变形温度的升高，η先升高后下降。整体来说，合金在应变速率为1～10 s-1时的η较小，当应变速率为10 s-1和变形温度为900 ℃时，合金的η取最小值约为0.17；η最高的区域出现在图中星型所示处，合金在低应变速率(0.01 s-1)和980 ℃左右时的功率耗散效率η最大，其值大于0.94。

图7 Ti62421s合金的加工图Fig.7 Processing Map of Ti62421s alloy

(1) 功率耗散效率 η值小于 30%的区域，如图 7中的阴影区。该区域主要集中在应变速率为1 s-1区域以及900～940 ℃低温区，该区域通常是失稳区，合金在变形过程中出现扭折等强烈的不均匀变形现象，如图2(c)所示。

(2) 功率耗散效率η为30%～55%的区域。该区域分为2部分：一部分主要集中区在应变速率为0.01～0.1 s-1和温度为940～1 020 ℃或者应变速率在0.01以下的低温区，另一部分为应变速率在10 s-1左右和温度在980 ℃附近的区域，该区域通常是典型的动态再结晶区域，如图2(a)所示。

(3) 功率耗散效率η大于55%的区域。该区域主要集中在温度 940～1 020 ℃的低应变速率区(ε˙＜0.1 s-1)，功率耗散效率η大于60%时，通常是开裂区或超塑性区。功率耗散效率达70%～85%，所以，该合金又可能发生超塑性变形行为。但这一结果还有待于进行下一步超塑成型实验加以证实。近 α高温钛合金IMI685 在 875～1 025 ℃和 0.001～0.1 s-1范围内发生超塑变形[28]。近 β型钛合金 TC17(Ti-5Al- 4Mo-4Cr-2Zr-2Sn)在 830 ℃和ε˙＝0.01 s-1时，发生超塑性变形[8]。在超塑性变形过程中，Ashby和 Verral认为，在晶界滑移的同时伴随有扩散蠕变，原子的迁移对晶界滑移起调节作用，由于超塑性变形过程中晶界的高迁移性，导致耗散效率较高[31]。

参照Ti62421s合金的热加工图，并考虑实际生产加工效率的问题，合金最佳变形工艺参数为：θ=980 ℃，ε˙=0.01～0.1 s-1。

3 结论

(1) Ti62421s钛合金是一种对温度和应变速率比较敏感的材料，其流变应力曲线具有应力峰值和变形软化特性，其变形抗力随着变形温度的升高而减小，随应变速率的增加而增大。合金在980 ℃以上的高应变速率下变形时，出现了应力不连续屈服现象。变形温度越高，变形速率越大，不连续屈服现象就越明显。该合金的不连续屈服现象，是大量可动位错在晶界塞集，导致变形从晶界向晶内扩展引起的。

(2) Ti62421s合金高温压缩变形材料常数如下：α=6.8×10-3MPa-1，n2=3.39 MPa，A=e41.42s-1，Q=416.418 32 kJ/mol。

通过线性回归分析，建立了相关的流变应力模型：

(3) 功率耗散效率的峰值区为变形温度范围在965～1 005 ℃，应变速率范围在 0.001 s-1区域，峰值效率为94%。基于动态材料学模型建立了Ti62421s的热加工图，得出合金最佳变形工艺参数为：θ=980 ℃，ε˙=0.01～0.1 s-1。

[1] 金方杰. 铝基复合材料的高温流变行为及加工图研究[D]. 上海: 上海交通大学出版社, 2008: 35-40.JIN Fang-jie. The research of flow stress behaviors at elevated temperature and processing maps for aluminum matrix composites[D]. Shanghai: Shanghai Jiaotong University Press,2008: 35-40.

[2] 覃银江, 潘清林, 何运斌, 等. ZK60镁合金高温流变本构模型[J]. 中南大学学报: 自然科学版, 2010, 41(5): 1774-1778.QIN Yin-jiang, PAN Qing-lin, HE Yun-bin, et al. Constitutive modeling for elevated temperature flow behavior of ZK60 magnesium alloy[J]. Journal of Central South University of Technology: Science and Technology, 2010, 41(5): 1774-1778.

[3] 林武, 李红英, 曾翠婷, 等. 一种低碳微合金管线钢的热变形行为[J]. 中南大学学报: 自然科学版, 2010, 41(3): 940-942.LIN Wu, LI Hong-ying, ZENG Cui-ting, et al. Hot deformation behavior for a kind of low carbon micro-alloy pipeline steel[J].Journal of Central South University of Technology: Science and Technology, 2010, 41(3): 940-942.

[4] 戚运莲. Ti600高温钛合金的热变形行为及加工图研究[M].西安: 西北工业大学出版社, 2007: 40-50.QI Yun-lian. Study on hot deformation behavior and processing map of high temperature titanium alloy Ti600[M]. Xi'an:Northwestern Polytechnical University Publishing Press, 2007:40-50.

[5] 韩远飞, 曾卫东, 赵永庆, 等. 基于模糊神经网络的Ti40合金高温本构关系模型[J]. 中国有色金属学报, 2010, 20(10):1971-1973.HAN Yuan-fei, ZENG Wei-dong, ZHAO Yong-qing, et al. High temperature constitutive relationship model of Ti40 alloy based on fuzzy-neural network[J]. Transactions of Nonferrous Metals Society of China, 2010, 20(10): 1971-1973.

[6] 余琨, 蔡志勇, 王晓艳, 等. 热轧 AZ31镁合金板材高温塑性变形行为[J]. 中南大学学报: 自然科学版, 2010, 41(5):1749-1753.YU Kun, CAI Zhi-yong, WANG Xiao-yan, et al. Hot plastic deformation of hot-rolled AZ31 Mg alloy plane[J]. Journal of Central South University of Technology, 2010, 41(5):1749-1753.

[7] Naravana Murty S V S, Nageswara Rao B. Themomechanical processing and heat treatment of Ti-6Al-2Sn-2Zr-2Cr-2Mo-Si for structural applications[J]. Materials Science and Engineering,1998, 16(3): 46-52.

[8] Su G, Prasad Y V. Flow cures and deformaton of metals at differnt temperayures and strain-rate[J]. Materials Science and Engineering, 1998, 17(8): 63-68.

[9] Prasad Y V, Seshacharyulu T. Processing maps for hotworking of titanium alloys[J]. Materials Science Engineering, 1997, 15(2):82-90.

[10] Menon S S, Rack H J. Flow stability of binary Al-Li alloys[J].Materials Science and Engineering A, 2001, 297: 244-255.

[11] Balasubrahmanyam V V, Prasad Y V R K. Deformation behaviour of beta titanium alloy Ti-10V-4.5Fe-1.5A1 in hot upset forging[J]. Materials Science and Engineering A, 2002,336: 150-158.

[12] 鲍如强, 黄旭, 曹春晓, 等. 加工图在钛合金中的应用[J]. 材料导报, 2004, 18(7): 26-29.BAO Ru-qiang, HUANG Xu, CAO Chun-xiao, et al. Application of processing maps in hot working of titanium alloy[J]. Materials Review, 2004, 18(7): 26-29.

[13] 薛克敏, 段园培, 李萍, 等. TB8 钛合金的热变形行为及加工图[J]. 材料工程, 2007, 增刊1: 57-60.XUE Ke-min, DUAN Yuan-pei, LI Ping, et al. Deformation behavior and processing map of high temperature deformation of TB8 alloy[J]. Journal of Materials Engineering, 2007(S1):57-60.

[14] 王志辉, 夏长清, 李学雄, 等. Ti62421s 钛合金 T(α+β)/β相变温度的测定与分析[J]. 稀有金属, 2010, 34(5): 663-667.WANG Zhi-hui, XIA Chang-qing, LI Xue-xiong, et al. Analysis and determination on T(α+β)/βtransformation point of Ti62421s titanium alloy[J]. Chinese Journal of Rare Metals, 2010, 34(5):663-667.

[15] 周军, 曾卫东, 舒滢, 等. 应用热加工图研究 TC17合金片状组织球化规律[J]. 稀有金属材料与工程, 2006, 35(2): 265-269.ZHOU Jun, ZENG Wei-dong, SHU Ying, et al. Study on globularization of lamellar α structure in TC17 titanium alloy during hot deformation using processing map[J]. Rare Metal Materials and Engineering, 2006, 35(2): 265-269.

[16] Li L X, Lou Y, Yang L B. Processing map for the hot working of near α titanium alloy 685[J]. Materials and Desin, 2002, 71(3):377-383

[17] Varin R A, Mazurek B, Himbeault D. Discontinuous yielding in ultrafine-grained austenitic stainless steels[J]. Materials Science and Engineering, 1987, 10: 109-119.

[18] Robertson D G, Mcshane H B. Isothermal hot deformation behaviour of (α+β) titanium alloy Ti-4Al-4Mo-2Sn-0.5Si (IMI 550)[J]. Materials Science and Technology, 1997, 13(7):459-468.

[19] Johnston W G,Gilman J J. Strength and structure under hotworkig condition[J]. J Appl Phys, 1959, 30: 129-144.

[20] Philippart I, Rack H J. High temperature dynamic yielding in metastable Ti-6.8Mo-4.SFe-1.SAI[J]. Materials Science and Engineering A, 1998, 243: 196-200.

[21] Kurzydlowski K J. On the discontinuous yielding of micro-grained FCC polycrystals[J]. Scripta Metallurgica et Materialia, 1992, 1: 283-286.

[22] Philippart L, Rack H J. Recrystallization in hot working and creep[J]. Materials Science and Engineering, 1998, 8(6):161-170.

[23] Burke J J, Mahrabian R. Advances in metal processing[M]. New York: Plenum Press, 1981: 133.

[24] Poirier J P. 晶体的高温塑性变形[M]. 关德林, 译. 大连: 大连理工大学出版社, 1989: 55-60.Poirier J P. High-temperature plastic deformation of the crystal[M]. GUAN De-lin, transl. Dalian: Dalian University of Technology Press, 1989: 55-60.

[25] 李杰, 尹志民, 黄继武, 等. 超高强 A1-Zn-Mg-Cu-Zr合金的热变形行为[J]. 稀有金属, 2004, 28(1): 166-170.LI Jie, YIN Zhi-min, HUANG Ji-wu, et al. Hot deformation behavior of Al-Zn-Mg-Cu-Zr alloy with super-high strength[J].Chinese Journal of Rare Metals, 2004, 28(1): 166-170.

[26] 杨立斌, 张辉, 彭大暑, 等. 7075铝合金高温流变行为的研究[J]. 热加工工艺, 2002(1): 1-5.YANG Li-bin, ZHANG Hui, PENG Da-shu, et al. Study of mechanic behavior for 7050 aluminum alloy under hot-working conditions[J]. Hot Working Technology, 2002(1): 1-5.

[27] Jonas J J, Sellars C M, MCWJ. Strength and structure under hot working conditions[J]. Tegart Int Metal Reviews, 1969, 14(130):1-4.

[28] Zhan Z, Real T, Dominique D. The Mg-Zn-A1 alloys and the influence of calcium on their creep properties[J]. Magnesium Technology 2001, Edited by J. Hryn, TMS (The Minerals,Metals & Materials Society), 2001: 147-151.

[29] Luo A A. Recent magnesium alloy development for elevated temperature applications[J]. International Materials Reviews,2004, 49(1): 13-30.

[30] Prasad Y V R K, Seshacharyulu T. Modelling of hot deformation for microstructural control[J]. International Materials Reviews,1998, 43(6): 243-258.

[31] 曾卫东, 周义刚, 周军, 等. 加工图理论研究进展[J]. 稀有金属材料与工程, 2006, 35(5): 676-680.ZENG Wei-dong, ZHOU Yi-gang, ZHOU Jun, et al. Recent development of processing map theory[J]. Rare Metal Materials and Engineering, 2006, 35(5): 676-680.