树的一种线性化算法

林淑飞

(北方民族大学计算机学院，宁夏银川750021)

树的一种线性化算法

林淑飞

(北方民族大学计算机学院，宁夏银川750021)

给出了一种树的线性化算法以及从线性化结果重构树的算法.这种线性表表示法比树的其它表示法更简洁、更易管理、更节约空间.在线性表表示方式下，实现了树的求结点双亲、求结点孩子、求树的高度3个运算.从具体实现过程可以看出，线性表表示法对树的常见运算的实现都比较方便.

数据结构;树;线性化;线性表

树是一种非线性结构.具体地说，树形结构是一种层次结构，这种层次结构的特点是，任一结点的前驱如果存在则一定是唯一的，后继如果存在则可以有多个.树形结构在计算机科学中的应用十分广泛，如在编译程序中，可用树表示源程序的语法结构;在数据库系统中，可用树来组织信息;在操作系统中，可用树组织文件.

树的各种操作的实现效率具体取决于树的表示方式.树的表示方式有很多，常用的有双亲表示法、孩子表示法和孩子兄弟表示法等.本文介绍一种线性表表示法，即一种树的线性化算法.需要说明的是，本文研究的树是有序的.

1 树的线性化算法

树的线性化简单地说就是将树中的结点用一个线性表来表示.线性化树要求不能丢失树的精确结构［1－2］，即对于任意结点应该能准确找到其父结点(若存在的话)和其所有的孩子结点(若存在孩子结点的话).

如果我们试图通过简单地按层从上到下的顺序列出树中的结点来线性化树，就可能会丢失树的精确结构.例如，若用线性表L:(A)(BCD)(EFG) (HI)线性化图1所示的树，就无法知道F是C的孩子还是D的孩子.出现这种情况的原因是，我们将同一层上具有不同双亲的结点放在了一个括号中.若将线性表L中的(EFG)分成(EF)(G)，即用线性表(A)(BCD)(EF)(G)(HI)表示图1所示的树，仍然有错误，因为无法知道E、F是B的孩子，还是C的孩子［3］.避免这个错误的一种方式是，如果某个结点是叶结点，但是按照从上到下、从左到右的顺序，在它之后有非叶结点，那么需要用一个空括号来虚拟此叶结点的孩子.例如，图1所示的树中，B是叶结点，依从上到下、从左到右的顺序，C是在它之后，但C不是叶结点，所以需用“()”虚拟B的孩子，树的线性化结果为:(A)(BCD)()(EF)(G) (HI)［4－7］.

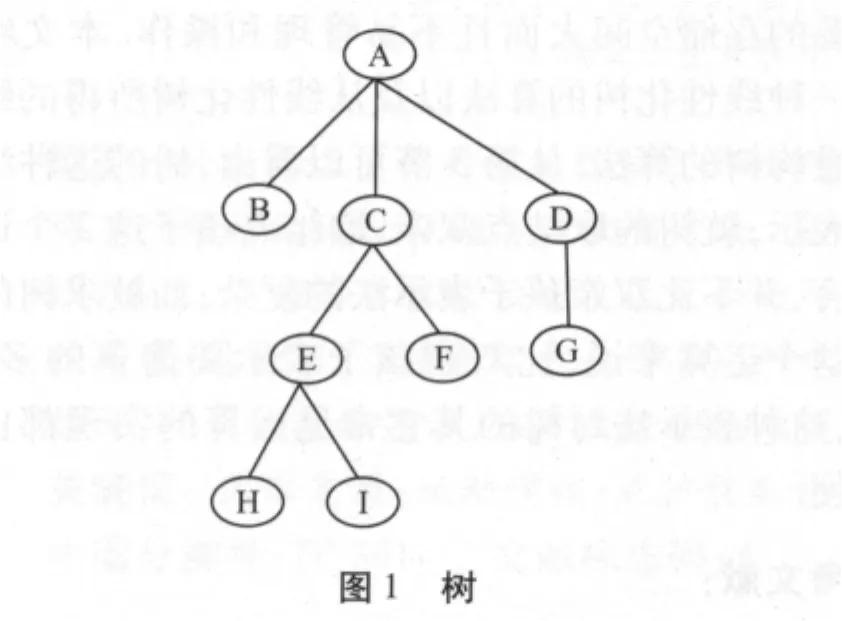
树的这种线性化算法具体描述如下，设T表示树，L表示将T线性化所得的线性表，i为指针，sum为整型变量，初始L为空、sum为0.

Step 1若T为空，则算法结束;否则转Step 2;

Step 2L=L+“(”+T的根结点+“)”，并令i指向L的头元素;

Step 3i向后移动，直到遇到一个T中的结点;

Step 4若i所指结点不是叶结点，L=L+“(”+ i所指结点的所有孩子结点+“)”;否则L=L+“()”;

Step 5sum=sum+1;

Step 6如果sum等于T的结点个数，转Step 7，否则转Step 3;

Step 7删除L末尾的若干个“()”，算法结束.

2 树的重构算法

上述树的线性化算法所得的线性表，和树是一一对应的.1棵树可以线性化成1个唯一的带若干括号的线性表，反之也成立.当然并不是任意一个带若干括号的线性表都可重构成一棵树.例如，(AB) (CD)就不能重构成树，因为根结点不能有2个; (A)(BC)()()(DE)也不能表示一棵树，因为D、E成了无前驱的结点.

下面给出由树的线性化算法所得的线性表重构树的算法.为了说明方便，设L表示线性表，且L以“#”结束;T用来描述树，T={D，R}(D是结点的集合，R是关系的集合，初始D和R均为空).

算法描述如下:

Step 1如果L为空表，则T为空，算法结束;否则转Step 2;

Step 2如果L只有1个括号，则D中增加1个元素，即树的根结点，R仍为空，算法结束，否则转Step 3;

Step 3令指针i指向L的第1个“(”，指针j指向L的第2个“(”;

Step 4i向后移动，直到遇到j或遇到1个T中的结点;

Step 5如果i和j相遇，说明L不能重构成1棵树，算法结束;否则转Step 6;

Step 6D=D+{i所指元素};

Step 7j向后移动，指向L的下一个元素;

Step 8如果j所指元素为“)”，转Step 7;如果j所指元素为“#”，转Step 10;如果j所指为“(”，转Step 4;如果j所指元素为其它，转Step 9;

Step 9R=R+{i所指元素，j所指元素}，转Step 7;

Step 10i向后移动，直到遇到“#”或遇到1个T中的结点;

Step 11如果遇到“#”，算法结束，否则转Step 12;

Step 12D=D+{i所指元素}，转Step 10.

3 线性化树的基本操作

树的基本操作有求树根、求非根结点的双亲、求某结点的孩子、求某结点的左右兄弟等等.线性化树的这些基本操作都是十分方便的，下面以求结点的双亲、求结点的孩子、求树的高度这3个操作为例说明［8－9］.

3.1 求结点的所有孩子

从树的线性化过程可以看出，每个括号都是用来存放某个结点的所有孩子，包括空括号，空括号说明某结点无孩子.这样，除了第1个括号内是根结点，其余每个括号内依次存放着每个结点的所有孩子，例如，(A)(BC)()(DE)(F)()(GH)(I)所表示的树中，A是根结点，第2个括号中的B、C是A的孩子，第3括号包含着B的孩子(第3个括号为空，说明B是叶结点)，第4个括号包含着C的孩子，第5～8个括号分别包含着D、E、F、G的孩子，H和I显然是叶结点.

所以要求某个结点的所有孩子，只需在表示树的线性表中确定此结点是第几个结点，“(”和“)”不计.如果某结点是第n个结点，那么它的孩子就在第n+1个括号中.若第n+1个括号为空或不存在第n+1个括号，说明此结点为叶结点.如在(A) (BC)()(DE)(F)()(GH)(I)中，E是第5个结点，所以E的孩子在第6个括号内，即E是叶结点; G是第7个结点，所以G的孩子在第8个括号内，即I是G的孩子.

3.2 求结点的双亲

与求结点的孩子的过程相逆，欲求某结点的双亲，先看此结点在线性表中的第几个括号内.如果此结点在第n个括号内，那么树的线性表中第n－1个结点就是其双亲，注意“(”和“)”不计数.例如，在(A)(BC)()(DE)(F)()(GH)(I)中，H是在第7个括号内，所以H的双亲是第6个结点F;D是在第4个括号内，所以D的双亲是第3个结点C.

需要注意的是，如果某个结点是在线性表的第n个括号内，但是线性表中第n－1个结点却在此括号内或后，即在第m(m＞=n)个括号中，这样就说明此线性表并不能被重构成1棵树.例如，(A) (BC)()(DE)()()(HI)中，H是在第7个括号内，但是第6个结点也在第7个括号内，所以此线性表是非法的，并不能表示1个棵树.

3.3 求树的高度

树的高度与表示树的线性表中的括号数和结点个数有着密切的关系.所以遍历线性表的同时，可计算出树的高度.

计算树的高度的具体方法如下.假设L表示线性表，以“#”结束;Depth表示树的高度，初值为0; now表示当前层的结点数，初值为1;i是遍历L的指针变量;

Step 1i指向L的头元素;计数变量x=0，y=0;

Step 2如果i所指元素为树的结点，则x++;如果i所指元素为“)”，则y++;如果i所指元素为“#”，则转Step 5;

Step 3判断y与now是否相等.如果y=now，则Depth++，now=x，x=0，y=0;

Step 4i向后移动，指向L的下一个元素，并转Step 2;

Step 5Depth++，算法结束.

4 结语

树的几种表示法中，对树的运算而言，双亲孩子表示法较其它表示法更方便.但是双亲孩子表示法需要的存储空间大而且不易管理和操作.本文给出了一种线性化树的算法以及从线性化树所得的线性表重构树的算法.从第3节可以看出，树的这种线性化表示，就树的取结点双亲、取结点孩子这2个运算而言，并不比双亲孩子表示法的复杂;而就求树的高度这个运算来说，比双亲孩子表示要简单的多.其实，这种表示法对树的其它常见运算的实现都比较方便.

［1］HAREL D.算法学——计算精髓［M］.3版.霍红卫，译.北京:高等教育出版社，2007.

［2］万常选，刘喜平.XML数据库技术［M］.2版.北京:清华大学出版社，2008.

［3］MEYER A R，RITCHIE R.The complexity of loop programs［C］//ACM＇67 Proceedings Of The 1967 22nd National Conference.New York:ACM Press，1967.

［4］ZHANG N，KACHOLIA V.A succinct physical storage scheme for efficient evaluation of path queries in XML［C］//Proceeding of the 20th International Conference on Data Engineering(ICDE 2004).Boston:IEEE Computer Society，2004:54－65.

［5］吴恒山，段雄文.叶结点编码四叉树的邻域寻找算法［J］.计算机应用，2005，25(11):2624－2626.

［6］张群洪，陈崇成.一种改进的动态二叉树的自组织神经网络算法［J］.计算机应用，2007，27(9):2262－2267.

［7］叶晓彤，邓云.基于唯一二叉树的XML函数表达式标识转换［J］.计算机工程，2009，35(10):75－77.

［8］胡顺仿，向云强.基于JXTA的平面几何辅助教学系统设计与实现［J］.云南民族大学学报:自然科学版，2011，20(2):139－143.

［9］宋金歌，杨景，陈平，等.一种非负矩阵分解的快速稀疏算法［J］.云南民族大学学报:自然科学版，2011，20 (4):262－266.

(责任编辑庄红林)

A Linearization Algorithm of the Trees

LIN Shu-fei
(Department of Computer Science，Beifang Ethnic University，Yinchuan 750021，China)

A linearization algorithm of the trees is given.The algorithm with the reconstruction of the trees from the linearization result is designed.This linear representation of the trees is more concise，more space－saving，easier to manage than any other notation.In this linear representation，parent and children of the trees are found and the depth of the trees is calculated.From the process of realization，it has been proved that this method is very convenient in the common operations of the trees.

data structure;trees;linearization;linear list

TP 312

A

1672－8513(2012)04－0298－03

10.3969/j.issn.1672－8513.2012.04.017

2012－03－29.

北方民族大学基金(2011Y028).

林淑飞(1979－)，女，硕士，讲师.主要研究方向:算法分析与设计.