基于二次傅里叶频谱的运动模糊方向精确检测

郭红伟，田益民，付波

(1.红河学院工学院，云南蒙自661100;2.北京印刷学院基础部，北京102600; 3.湖北工业大学电气与电子工程学院，武汉430068)

基于二次傅里叶频谱的运动模糊方向精确检测

郭红伟1，田益民2，付波3

(1.红河学院工学院，云南蒙自661100;2.北京印刷学院基础部，北京102600; 3.湖北工业大学电气与电子工程学院，武汉430068)

针对运动模糊图像的模糊方向检测问题，分析了运动模糊图像的频谱特性，提出基于二次傅里叶频谱的运动模糊方向检测方法.首先，对模糊图像做2次傅里叶变换得到二次傅里叶频谱;其次，对频谱各像素按灰度值大小做排序，取排序第100的像素灰度为阈值使频谱转换为二值图像;最后，过二值图像中心作不同斜率的直线，通过计算所有亮点到直线的距离确定运动模糊方向.实验数据显示，该方法检测运动模糊方向的精度高，且具有较强的抗噪声能力.

图像复原;运动模糊;点扩散函数;傅里叶变换

运动模糊图像的复原是图像复原中的重要课题之一，随着科学技术的不断发展，它在各个领域中的应用越来越多，要求也越来越高，可广泛应用于天文、军事、道路交通、医学图像、工业控制及刑侦领域，具有重要的现实意义.而图像复原的关键在于点扩散函数(point spread function，PSF)的准确鉴别，若PSF已知，则可以用维纳滤波、约束最小二乘方滤波等算法获得复原图像.运动模糊是由于拍照时相机与景物的相对快速运动导致同一时刻不同景物点在电荷藕合器件(charge－coupled device，CCD)的同一点同时曝光引起的，由于物体运动都有一定的惯性，在摄取图像的短暂曝光时间内，一般可认为是匀速直线运动.匀速直线运动模糊的PSF由运动模糊方向和模糊尺度2个参数确定，对于模糊尺度的估算，文献［1－4］均是以水平方向的运动模糊进行研究，因为任意方向的运动都可以通过图像旋转将模糊方向旋转到水平轴方向.因此，运动模糊方向的精确检测是估算模糊尺度和运动模糊图像复原的关健.

近年来，出现了许多检测运动模糊方向的方法，文献［5－6］利用Radon变换检测运动模糊图像频谱中的亮、暗条纹得到模糊方向;文献［7］在此基础上对频谱先进行二值化再用Radon变换检测，检测精度有所提高;文献［8］也是先对频谱进行二值化，然后用霍夫变换检测模糊方向;文献［9－10］提出在空域对模糊图像做不同角度微分后求和，最小值对应角度为模糊方向，其估计误差较大，特别当模糊图像纹理较少且存在大面积平滑区域时，将出现估计错误;文献［11］利用运动模糊图像倒谱的极小值(为负数)点坐标，采取几何运算方式估算模糊方向;文献［12］对倒谱取绝对值后用Radon变换鉴别模糊方向.以上文献对运动模糊图像做了大量研究，但是，运动模糊方向检测的准确性，计算的高效以及方法的抗噪声能力仍是值得关注的重点问题.

本文提出基于二次傅里叶频谱的运动模糊方向检测方法.通过对运动模糊图像进行2次傅里叶变换，对二次傅里叶频谱灰度值做排序，取某个排序灰度为阈值把频谱变为二值图像，计算二值图像中亮点到过图像中心直线的距离确定运动模糊方向.实验数据显示，该方法检测运动模糊方向的精度高，能适用于小尺度运动模糊的模糊方向检测，且具有较强的抗噪声能力.

1 运动模糊图像的频谱特性

假设图像f(x，y)有一个平面运动，令x0(t)和y0(t)分别为t时间内在x和y方向上运动的变化分量，T表示成相系统记录介质的曝光时间.在不考虑噪声影响的情况下，运动模糊退化图像为:

式(3)大括号内积分项是f(x－x0(t)，yy0(t))的傅里叶变换，由时移特性得:

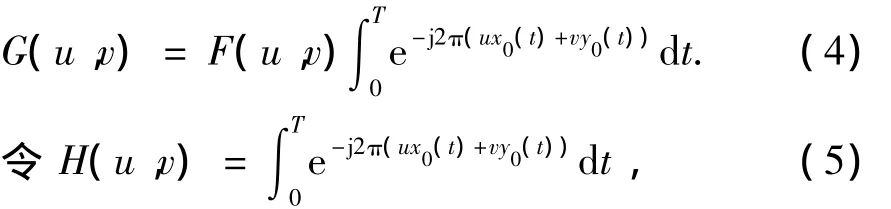
则得运动模糊图像退化的频域表述为:

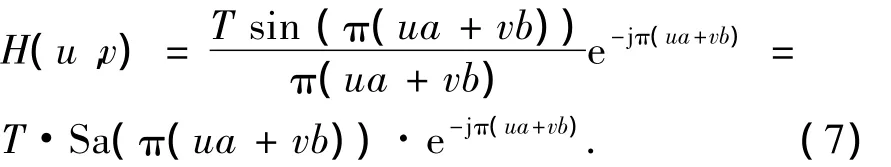
式(7)中Sa(π(ua+vb))称作取样函数，令γ= π(ua+vb)，则γ=0时取样函数为最大值1，γ= nπ(n是不为0的整数)时函数值为0.所以，H(u，v)在(ua+vb)=0时取得最大值T，(ua+vb)为非0的整数时，H(u，v)等于0.原始图像f(x，y)的傅里叶频谱通常是各向同性的，能量主要分布在低频区域.因此，由式(6)可知运动模糊退化图像的频谱中心会有一条较宽的亮带，平行于亮带两边将出现等间距的暗条纹，且越远离中心，条纹特征越弱.图1(a)、(b)是512×512像素的Lena原始图像和运动模糊图像(模糊尺度15像素，模糊角度45°).图1(c)、(d)是它们对应的傅里叶频谱图，频谱特征与理论分析一致.图1(d)的亮、暗条纹刚好与运动模糊方向垂直，文献［5－8］正是利用频谱的这一特征估计运动模糊方向的.

图像的纹理轮廓对应于傅里叶变换的高频，图像的平滑区域对应于傅里叶变换的低频，取样函数Sa(t)的傅里叶变换是一个门函数［13］:

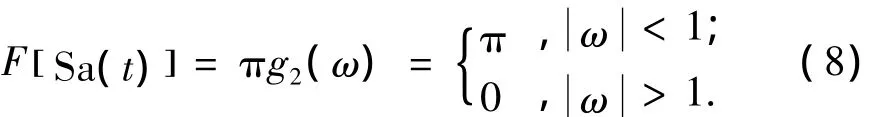
F[]·表示傅里叶变换运算符.图1(c)所示的Lena原始图像频谱较为平滑，因此对该频谱再做1次傅里叶变换后，能量完全集中在低频点上，如图1(e)所示.图1(d)所示的运动模糊图像频谱呈取样函数Sa(t)的形式，故对该频谱再做1次傅里叶变换后，能量集中在运动模糊方向上，如图1(f)所示，二次傅里叶频谱中出现1条与运动方向一致(45°)的亮条纹.需要说明的是:本节中的图1(c)～(f)均是把频谱0点移位到中心位置，且对频谱值取对数压缩灰度范围后的显示效果.由于二次傅里叶频谱的特征集中在中心点附近，为突出这些特征，图1(e)、(f)是剪切为192×192像素的显示效果.

2 运动模糊方向检测

由上节分析可知，在运动模糊图像的二次傅里叶频谱中有1条与运动模糊方向一致的亮条纹，本文通过检测该条纹获得运动模糊方向，为提高检测精度，将对二次傅里叶频谱进行二值化预处理.具体步骤如下:

1)计算退化图像频谱G(u，v)，并且移位使u= 0，v=0位于中心位置，为压缩频谱的灰度值范围，取对数形式

2)对1)中结果重复相同步骤，得到运动模糊图像的二次傅里叶频谱，记作R(u，v);

3)对R(u，v)的各像素按其灰度值从大到小排序，记作Pn;取排序第100的像素灰度为阈值，把二次傅里叶频谱转换为二值图像，记作B(u，v)，即:

4)过二值图像中心(u0，v0)作不同斜率的直线，计算所有亮点到直线的距离并求和，最小值对应直线的倾斜角为模糊方向.对于大小为N×M的图像，N、M为奇数时，中心点在(N+1)/2列和(M+1)/2行;N、M为偶数时，中心点在(N/2)+1列和(M/2)+1行.过点(u0，v0)，倾斜角为α的直线方程为:

设亮点坐标为(un，vn)，则亮点到直线的距离为:

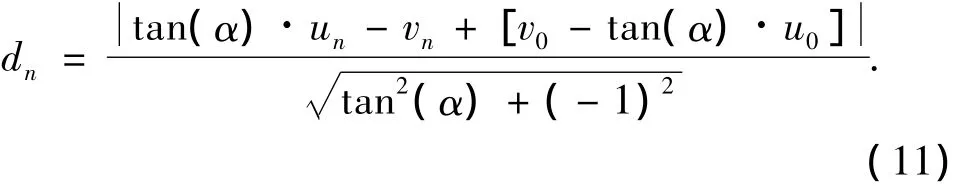
B(u，v)中所有亮点到倾斜角为α的直线距离之和为:

图2(a)是由图1(f)转换的二值图像，图2(b)是α取－90°到+90°时对应的Sα曲线，Sα最小值对应α为45°，与实际方向一致.由于α为90°时，斜率不存在，编程实现过程中，α取90°应单独处理，此时的

3 实验分析

为验证本文方法检测运动模糊方向的有效性，采用256×256像素的Lena标准测试图像进行仿真实验.表1为在不添加噪声情况下，对测试图像做不同模糊尺度和不同模糊角度的运动模糊，然后用文献［6］、［11］和本文算法进行模糊方向检测的结果.数据显示，模糊尺度较大时(如:20像素)，文献［6］和［11］的检测结果相对准确，检测误差不超过2°;模糊尺度小于10像素后，检测误差逐渐增大，文献［6］的结果已不能反映运动模糊方向.而本文算法在模糊尺度较大时，能精确检测出运动模糊方向，模糊尺度小于10像素时，检测误差也较小.

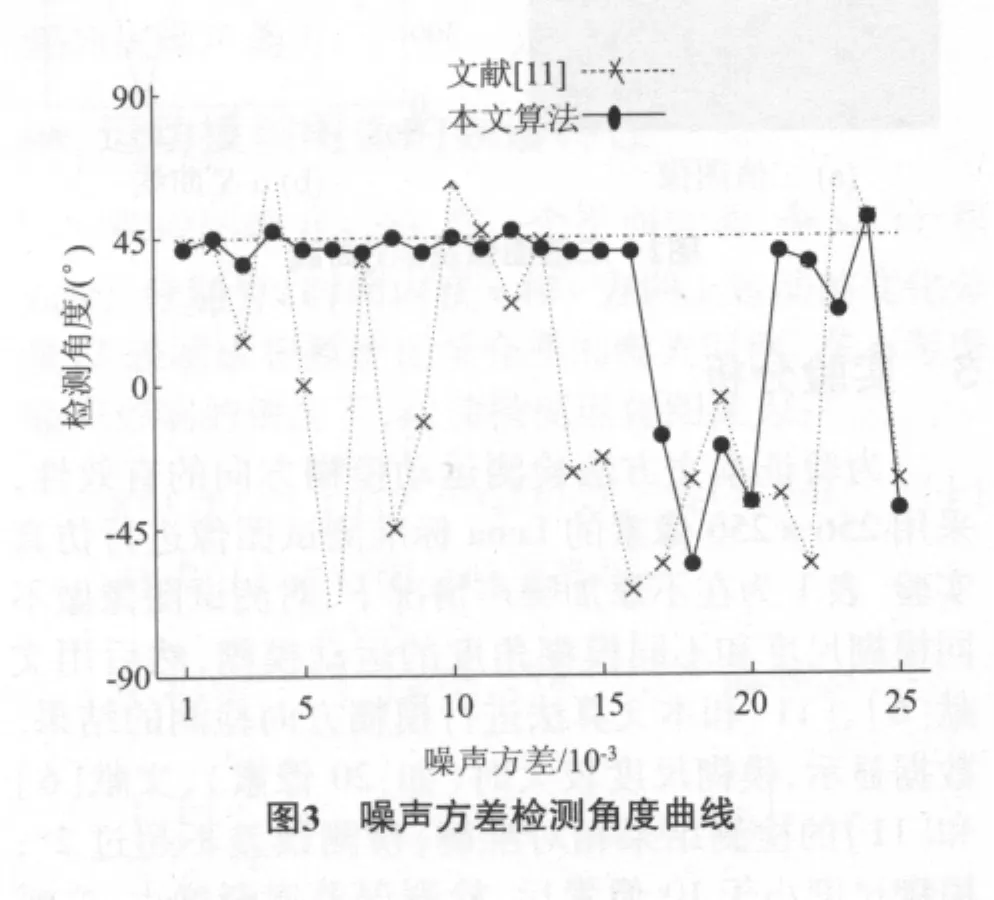
为验证本文方法的抗噪声能力，对Lena图像做模糊尺度为20像素，模糊方向为45°的运动模糊，然后添加均值为0，方差从0.001到0.025的高斯噪声.用文献［11］和本文算法检测不同强度噪声污染图像的模糊方向，图3是对应的噪声方差－检测角度曲线.曲线显示文献［11］仅在噪声方差小于0.002时能正确检测出运动模糊方向，方差大于0.002后检测结果严重偏离45°.本文算法在噪声方差小于0.016时的检测结果在45°左右，能正确反映运动模糊方向.

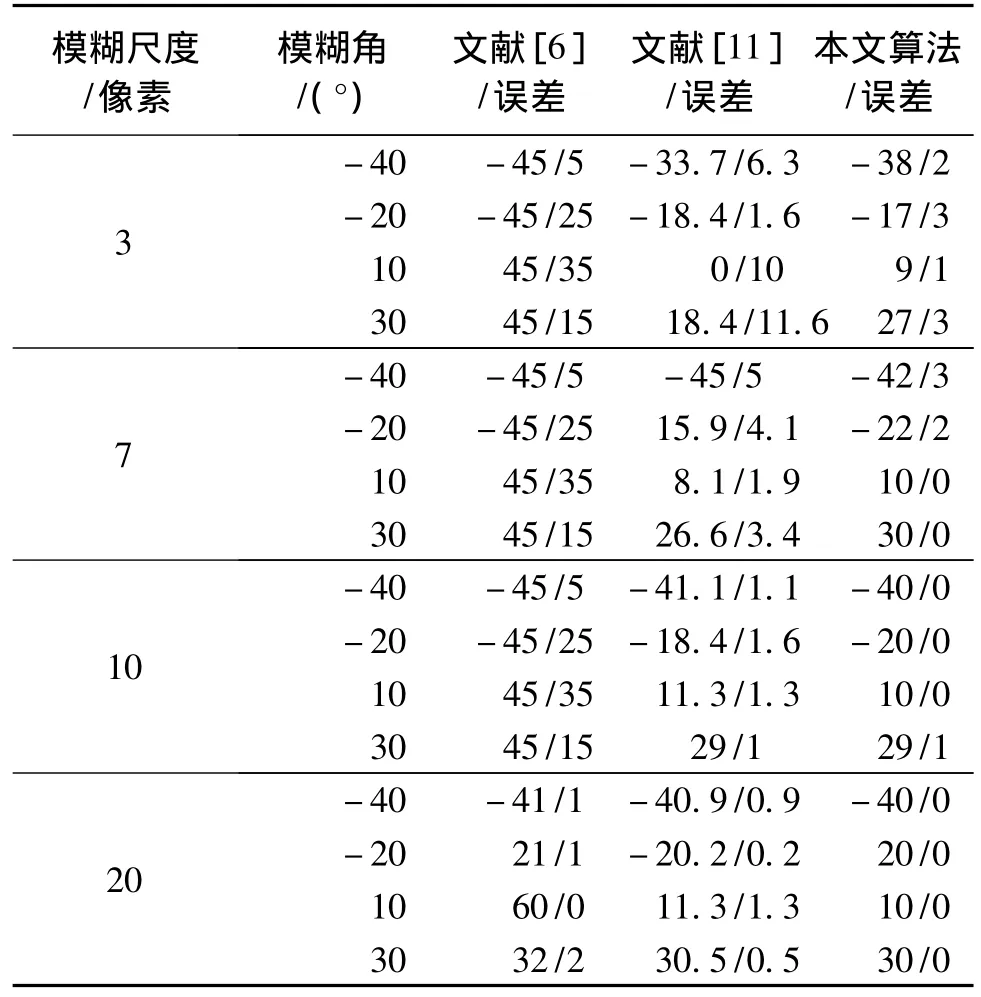
表1 512×512像素的Lena图像实验数据

4 结语

分析了运动模糊图像的频谱特性，揭示在运动模糊图像的二次傅里叶频谱中有1条与运动模糊方向一致的亮条纹，给出了检测该亮条纹方向的精确数值计算方法.通过对Lena标准测试图像的实验数据证明，该方法检测运动模糊方向精度高，能适用于小尺度运动模糊图像的模糊方向检测，且具有较强的抗噪声能力.图像长、宽不相等时，模糊图像的一次傅里叶频谱亮、暗条纹方向与运动方向不再垂直，而二次傅里叶频谱中亮条纹方向始终与运动模糊方向一致，故利用二次傅里叶频谱检测模糊方向时无须要求测试图像长、宽相等.

［1］张荣，杨建朝，张倩，等.SAR图像运动模糊参数估计［J］.电子学报，2007，35(10):2019－2022.

［2］郭永彩，丁小平，高潮.基于差分自相关的运动模糊图像尺度参数识别［J］.光电工程，2011，38(6):134－140.

［3］邸慧，于起峰.基于自相关的匀速运动模糊尺度参数识别［J］.国防科技大学学报，2006，28(5):123－125.

［4］贺卫国，黎绍发.匀速直线运动模糊长度的精确估计［J］.计算机应用，2005，25(6):1316－1317.

［5］MOGHADDAM M E，JAMZAD M.Finding point spread function of motion blur using radon transform and modeling the motion length［C］//Proceedings of the 4th IEEE International Symposium on Signal Processing and Information Technology.Italy:Rome，IEEE，2004:314－317.

［6］邓泽峰，熊有伦.基于频域方法的运动模糊方向识别［J］.光电工程，2007，34(10):98－101.

［7］李宇成，贾宝华，杨光明.运动模糊图像的参数估计与恢复［J］.计算机工程与设计，2010，31(19):4247－4249.

［8］LOKHANDE R，ARYA K V，GUPTA P.Identification of parameters and restoration of motion blurred images［C］// Proceedings of the 2006 ACM Symposium on Applied Computing.USA:New York，ACM，2006:301－305.

［9］YITZHAKY Y，KOPEIKA N S.Identification of Blur Parameters from Motion Blurred Images［J］.Computer Vision Graphic Image Processing:Graphical Models and Image Processing，1997，59(5):310－320.

［10］陈前荣，陆启生，成礼智.运动模糊图像的运动模糊方向鉴别［J］.国防科技大学学报，2004，26(1):41－45.

［11］谢伟，秦前清.基于倒频谱的运动模糊图像PSF参数估计［J］.武汉大学学报:信息科学版，2008，33(2): 128－131.

［12］郭红伟，朱家兴，寸宁.基于倒谱分析的运动模糊参数估计［J］.云南民族大学学报:自然科学版，2012，21 (2):150－153.

［13］吴大正，杨林耀，张永瑞，等.信号与线性系统分析［M］.4版.北京:高等教育出版社，2005:145－146.

(责任编辑庄红林)

Accurate Detection of the Motion Blurred Direction Based on Twice Fourier Spectrum

GUO Hong-wei1，TIAN Yi-min2，FU Bo3
(1.Engineering School，Honghe University，Mengzi 661100，China; 2.Department of Basic Science，Beijing Institute of Graphic Communication，Beijing 102600，China; 3.School of Electrical and Electric Engineering，Hubei University of Technology，Wuhan 430068，China)

Aiming at solving the problem related to the blurred direction of motion blurred image，the spectrum characteristics of the motion blurred image were analyzed and a method for detecting the motion blurred direction based on twice Fourier spectrum was proposed.Firstly，the twice Fourier spectrum of blurred image was calculated.And then all pixels from big to small in the spectrum were sorted out by grayscale value，the 100th largest grayscale value was selected to be a threshold to transform the spectrum to a binary image.Finally，by drawing straight lines of all slopes through the center of the binary image，the motion blurred direction was ascertained by calculating the distances from all bright spots to the straight line.The experiment results show that the method has high accuracy and good anti－noise ability.

image restoration;motion blur;point spread function;Fourier transform

TP 391

A

1672－8513(2012)04－0301－04

10.3969/j.issn.1672－8513.2012.04.018

2011－12－25.

国家自然科学基金(61178092，61072130).

郭红伟(1980－)，男，硕士，讲师.主要研究方向:数字图像复原.