波浪影响下导管架调平系统最优控制
房晓明, 姜沛然, 王立权, 弓海霞, 王影
(1.哈尔滨工程大学机电工程学院,黑龙江哈尔滨 150001;2.哈尔滨东安发动机(集团)有限公司,黑龙江哈尔滨 150066)
0 引言
目前,近海海上油田开发应用最广泛的一种平台结构类型是钢制导管架平台。该类平台由导管架、钢管桩和平台上部结构组成。导管架作为平台的基础,先在陆上预制,然后通过驳船拖运或水中浮拖至安装现场就位,经过打桩、调平和灌浆后导管架被安装固定在海床上。平台上部结构直接安装在导管架顶部,包括:所有生产设备、生活设施和直升飞机平台等安全设施,可用来钻井和采油。
导管架在安装过程中调平是整个安装过程中最重要的一个环节,其精度直接影响到平台的安全性、适应性、使用寿命等各种性能。在较深水域作业时,依靠海底整平、调整打桩顺序和使用过渡段技术等都很难达到平台上部结构的安装精度要求。由于风、浪以及作业船舶性能对调平作业效果影响很大。导管架安装后的水平度,需要使用导管架调平系统来完成[1-3]。
目前国内外进行导管架的调平作业是使用调平器分别对导管架4个边角桩腿进行独立调整,重复操作调整不同桩腿,直至导管架符合水平度要求。传统的调平方式尽管比较成熟,但由于没有完整而准确的调平控制系统,存在以下弊端:1)分别对4个桩腿进行调平作业,每个桩腿需要反复调整多次,调平作业效率低;2)每次单独调整一个桩腿,无法体现统一的调平策略和目标,调平精度和效果不易控制;3)单独调平某个桩腿,另外的桩腿可能会出现失载或过载状态,导致导管架的大部分重量由一个调平器承担,使调平器承载过大,对调平系统力学性能增加了更严格的要求;4)深水导管架受随机波浪载荷影响动力响应复杂,调平作业不易控制;5)不能形成一套统一的调平控制方法,对同一导管架有不同的调整方案,人为因素较大[4-6]。
波浪影响下的导管架调平系统属于典型的复杂高阶非线性系统,本文针对4桩腿式导管架提出了基于Mamdani模糊系统的液压自动调平的最优控制算法,利用模糊控制理论对安装在4个桩腿上的4组调平液压系统进行同时控制,制定出调平策略,不需建立调平系统的准确模型,对非线性调平系统有良好的控制效果。
1 调平系统结构及几何模型
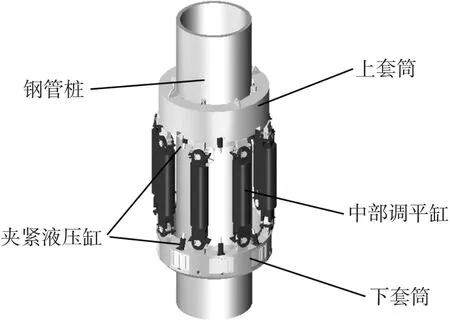
图1 调平器结构示意图Fig.1 Structure of leveling device
导管架调平器的主体机械结构主要由上套筒、下套筒以及中部调平机构3部分组成,如图1所示。上套筒内部装有向内夹持机构,8个液压缸伸出时使夹爪夹紧钢管桩,下套筒外部装有外胀夹持机构,驱动夹爪向外胀紧套筒进而与导管架腿部连接,中部调平机构包括8个调平液压缸,通过调整8个调平液压缸的伸缩调整导管架桩腿高度,达到导管架调平目的。
调平系统的几何模型如图2所示。
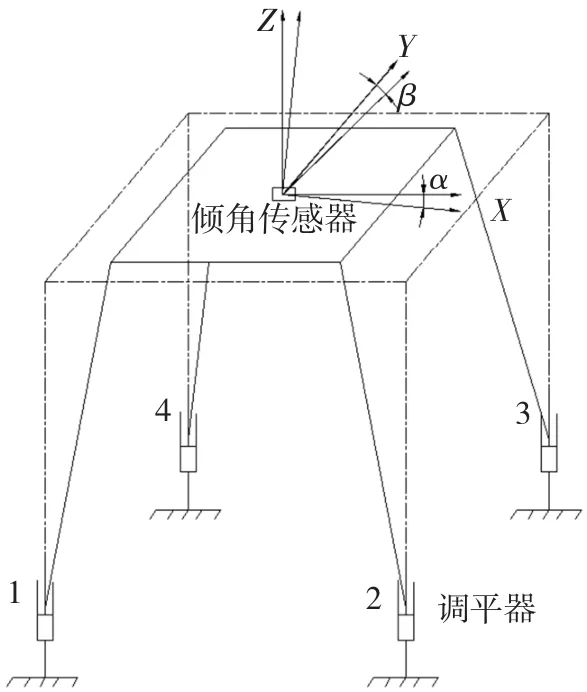
图2 调平系统几何模型Fig.2 Geometric model of leveling system
对于陆上4腿平台的调平系统主要有3支承和4支承两种调平方案。3支承调平方案比较容易实现,但抗倾覆能力差。4支承调平方案抗倾覆能力强,但存在静不定问题,容易产生“虚腿”的问题,静不定次数越高,系统越复杂[7-8]。本调平系统采用4支承调平方案,在导管架顶面中心安装一个双轴倾角传感器,分别检测横滚角和俯仰角的倾斜度的变化。以导管架顶面中心坐标为原点建立坐标系,X轴向倾角为α,Y轴向倾角为β。
设导管架主尺寸为L1×L2,导管架与X,Y方向的倾角分别为α,β,从导管架坐标系到水平坐标系的转换矩阵为

如图2所示,设导管架坐标系先绕y轴旋转α角,再绕x轴旋转β角,变换到水平坐标的位置,正负值依据右手定则确定。以导管架中心为坐标原点,根据导管架4个腿的坐标,通过坐标变换矩阵算出每个腿在水平坐标中的高度值h1、h2、h3、h4。
以腿1的高度h1为例,导管架尺寸为L1×L2,所以腿1在导管架坐标系的坐标值为[-L1/2,-L2/2,0]T,则其在水平坐标系的坐标为
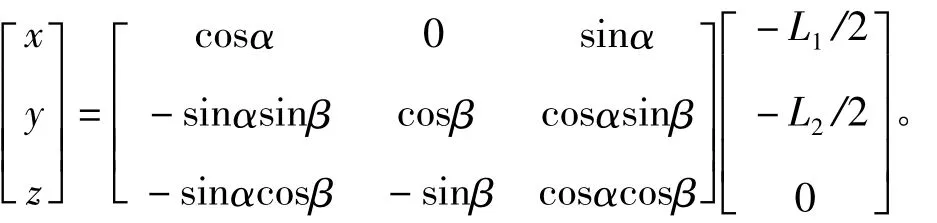
调平系统调平过程只需关心高度分量,也即其坐标的Z轴分量的大小,1腿高度为
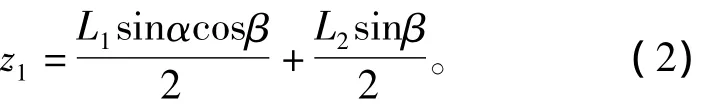
其余3腿高度的计算方法同理。
导管架调平前与调平后的平面夹角用倾斜矢量γ(γ,θ)来表示,矢径γ大小表倾斜角的大小,矢角θ的大小代表倾斜的梯度方向,按照几何关系可得倾斜矢量与α,β的关系为
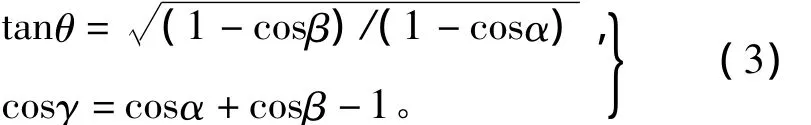
在调平过程中,矢量γ(γ,θ)的矢径γ不断缩小,一直达到满足精度要求为止,矢角θ的变化根据调平策略不同而不同。
对于4腿导管架,位置误差控制调平法采用半升半降向中间点逼近方式。
导管架在海底就位后,调平器下套筒的夹爪夹紧导管架桩腿套管,在调平缸完全伸出后上套筒的夹爪夹紧钢管桩,调平缸收缩至一半将导管架提起后,各桩腿根据系统控制分别通过上升和下降的调整动作向中间点靠拢,直到导管架达到水平度要求,经实验验证此调平策略的调平速度最快。
2 受控对象数学模型
调平系统采用双输入单输出的模糊控制算法,模糊控制调平系统原理如图3所示。
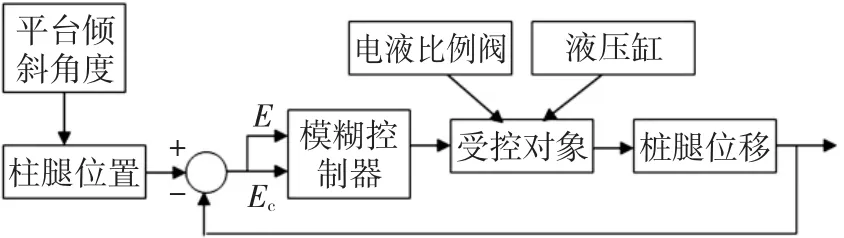
图3 控制系统原理图Fig.3 Principle diagram of control system
受控对象包括电液比例阀和液压缸。按照电液比例方向阀在实验中的分析结论,其传递函数可用二阶震荡环节近似表示为[9]

式中:Kq为阀的流量增益;ωv为阀的固有频率;δv为阀的阻尼比。
导管架调平器液压缸在数学分析中常采用传递函数表示为
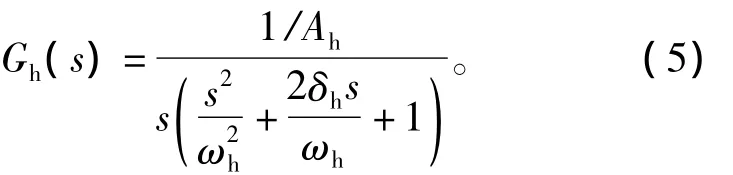
式中:Ah为液压缸有效面积;ωh为液压缸固有频率;δh为液压缸阻尼比。
根据式(4)和式(5)可得受控对象的传递函数为
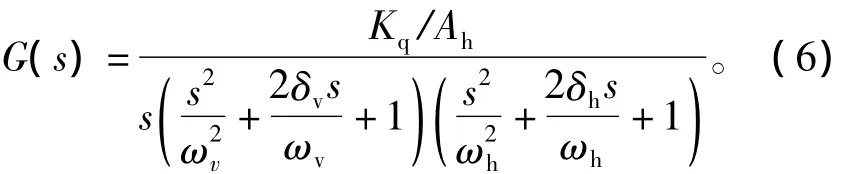
根据所选比例阀参数和设计液压缸的参数可知,s4、s4的系数极小,为了简化计算可忽略不计。
3 模糊控制调平系统
导管架调平模糊控制系统原理如图3所示。
设调平液压缸最大行程为1.2 m,因为采用向中心逼近的调平方式,因此选取高度误差E的论域为[-0.6,0.6],根据液压缸最大速度为 0.001 m/s,变化率Ec的论域为[-0.001,0.001],控制量U控制阀的开度的论域为[-1,1],正负值分别控制液压缸的升高与降低。
模糊控制规则依据工程师的经验确定。当误差E大或较大,确定控制量U以尽快消除误差为主;当误差E小或较小,确定控制量U以提高调平精度避免超调为主。
4 控制系统仿真
根据上述模型和控制算法,利用Matlab环境下的仿真工具SIMULINK建立系统的仿真模型,仿真总体框图和模糊控制器示意图分别如图4和图5所示。
1)无环境载荷影响下调平系统仿真
导管架根据平台使用功能的要求,其需要达到的水平度有所区别,仿真中设定初始传感器检测倾角X轴向倾角α=0.8°,Y轴向倾角为β=-0.5°,设定平台水平精确度要求即矢径γ大小不大于0.01°,调平系统仿真结果如图6、图7所示。
图6中显示的为各支撑桩腿相对与调平中间点的高度差随时间变化逐渐趋于0的过程,也即导管架调平的过程,通过图7中α、β和矢径γ变化曲线图也可看出,导管架随调平时间变化趋水平的过程。
反映导管架倾斜方向的参数矢角变化曲线如图8所示。
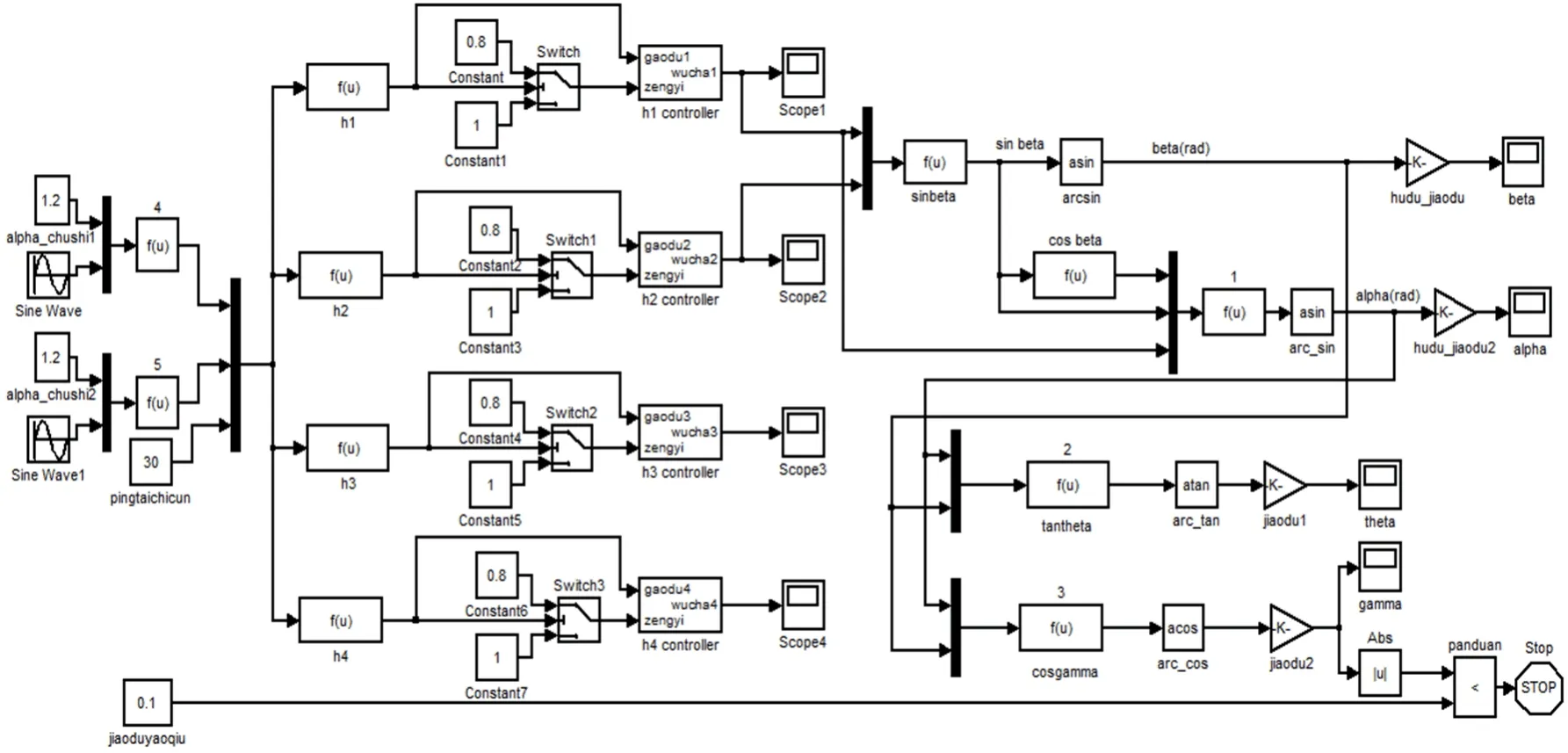
图4 仿真总体框图Fig.4 Block diagram of simulation
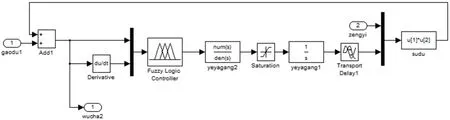
图5 模糊控制器框图Fig.5 Block diagram of fuzzy controller
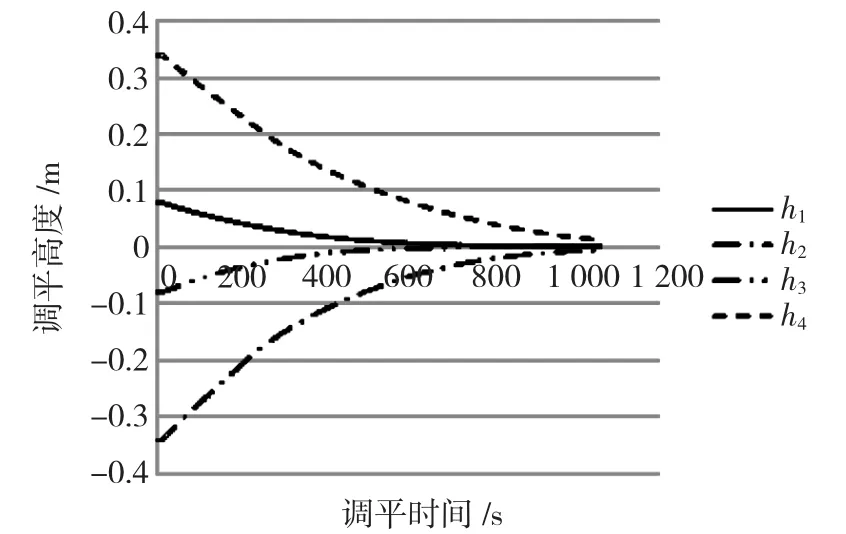
图6 调平过程各支撑桩腿高度变化曲线Fig.6 Curve of each leg height in leveling process
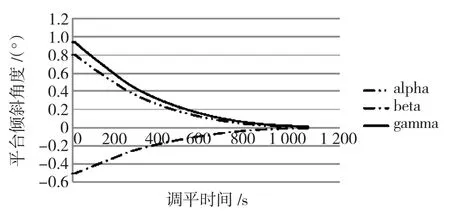
图7 调平过程平台倾角变化曲线Fig.7 Curve of platform angle in leveling process
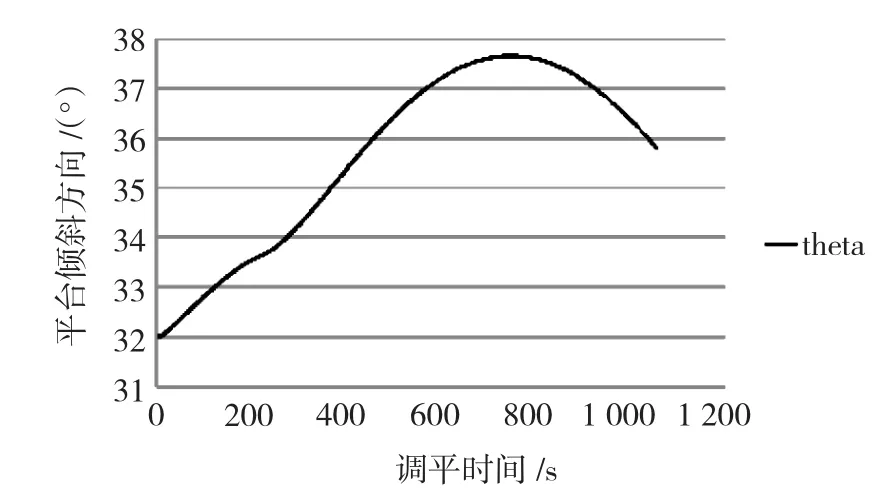
图8 调平过程平台倾斜方向变化曲线Fig.8 Curve of tilt direction in leveling process
2)波浪载荷影响下调平系统仿真
实际工程中,平台的用途不同,其导管架安装精度要求也有所差别,根据某平台《海上安装技术规格书》的要求,导管架安装后,其调平精度为对角线方向的水平误差不超过152 mm,设导管架对角线45 m,平台水平精度要求为arcsin(0.152/45)≈0.19°,由于导管架在波浪作用下会产生一定范围内的振动响应,根据资料分析,100 m高导管架在波浪的作用下其振动响应可达到100 mm幅度,其产生的角度变化经计算约为0.03°,因此考虑实际海况下调平系统的精度要求将大大降低,设为0.1°,但由于受到不确定的随机波浪载荷影响,因此要求系统必须具备较强的鲁棒性。为模拟海浪环境下调平系统的调平过程,在仿真环境中加入随机波浪干扰[10]。
实际波浪是一个连续的随机过程,将波浪的随机干扰沿X轴方向时输入时,α=0.9°,β=-1.2°仿真曲线如图9、图10和图11所示。
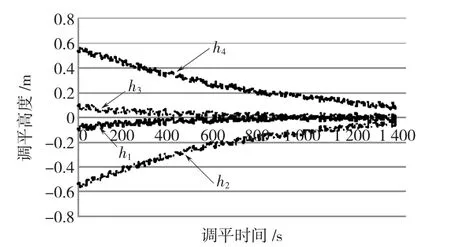
图9 随机波浪干扰各支撑桩腿高度变化曲线Fig.9 Curve of each leg height in leveling process with random wave interference
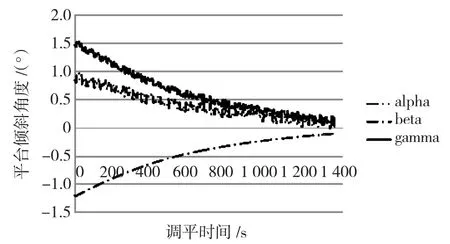
图10 随机波浪干扰倾角变化曲线Fig.10 Curve of platform angle in leveling process with random wave interference
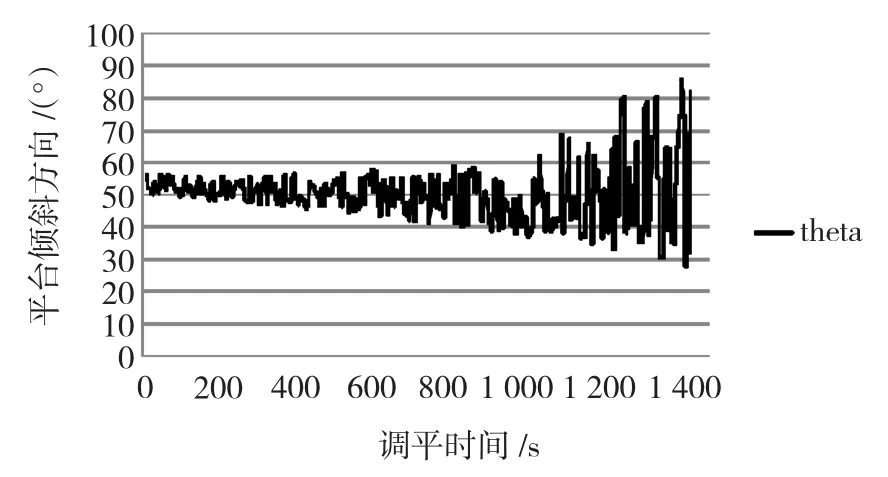
图11 随机波浪干扰平台倾斜方向变化曲线Fig.11 Curve of tilt direction in leveling process with random wave interference
5 结论
1)由随机干扰影响下调平系统的调平过程仿真中可以看出,随调平过程进行,各支撑桩腿趋近于中间点,导管架倾角也随之减小到要求的精度范围,根据仿真结果曲线可以看出,基于模糊控制的调平系统,具有较强的鲁棒性,可以解决传统调平方式存在的问题。
2)导管架倾斜方向随着导管架不断调平而变化幅度增大,即导管架趋于水平后,受波浪干扰其倾斜方向变化将会增大,主要是由控制策略引起。
3)为保证调平系统的实际应用,研制样机对调平系统进行实验研究将是下一步研究的主要工作。
[1]侯金林.导管架调平与灌浆系统[J].中国海上油气(工程),2000,12(4):20 -22.
HOU Jinlin.Jacket adjusting plane and grouting system[J].China Offshore Oil and Gas,2000,12(4):20 -22.
[2]DUAN Zhongdong,ZHOU Daocheng.Calibration of LRFD format for steel jacket offshore platforms in China offshore area[J].China Ocean Engineering,2006,12(1):1 -14.
[3]朱绍华.文昌油田深水导管架安装技术[J].中国海上油气(工程),2003,15(1):12 -14.
ZHU Shaohua.Deep water jacket of Wenchang oilfield installation technology[J].China Offshore Oil and Gas Engineering,2003,15(1):12-14.
[4]任新刚.钩扣式导管架调平器关键技术研究[D].哈尔滨:哈尔滨工程大学,2007.
[5]苏厚德,李金波,任永泉,等.海洋导管架在复杂载荷作用下的动态响应[J].石油化工设备,2011,40(6):35 -37.
SU Houde,LI Jinbo,REN Yongquan,et al.Dynamic response analysis of jacket platform under complex loads[J].Petro - chemical equipment,2011,40(6):35 -37.
[6]吴芳,赵德有.水对船舶与海洋建筑物结构振动影响的研究[J].中国海洋平台,2007,22(3):22 -26.
WU Fang,ZHAO Deyou.Effect of water on the ship and ocean engineering structure[J].China Offshore Platform,2007,22(3):22-26.
[7]凌轩,曹树平,朱玉泉,等.基于模糊自适应控制的四点支撑液压平台自动调平方法[J].机床与液压,2007,35(12):84-86.
LING Xuan,CAO Shuping,ZHU Yuquan,et al.Fuzzy self-adapting automatically leveling method for four supports hydraulic platform[J].Machine Tool& Hydraulics,2007,35(12):84 -86.
[8]王海淼,万彦辉,孟卫锋.自适应模糊PID控制在惯性平台数字调平系统中的应用[J].弹箭与制导学报,2005,25(3):145-147.
WANG Haimiao,WAN Yanhui,MENG Weifeng.The application of self-adaptive fuzzy PID control to the digital leveling system of platform INS [J].Journal of Projectiles,Rockets,Missiles and Guidance,2005,25(3):145 -147.
[9]高钦和.大型装置起竖过程的电液比例控制研究[J].机械工程学报,2004,40(2):189 -192.
GAO Qinhe.Study on electrohydraulic proportion control in largesize mechanism erecting process[J].Chinese Journal of Mechanical Engineering.2004,40(2):189 -192.
[10]嵇春艳.海洋平台动力响应分析与振动控制技术研究[D].青岛:中国海洋大学,2003.

