TCP网络的自适应神经滑模控制
叶成荫, 井元伟
(1.东北大学信息科学与工程学院,辽宁沈阳 110819;2.辽宁石油化工大学计算机与通信工程学院,辽宁抚顺 113001)
0 引言
随着传输控制协议(transmission control protocol,TCP)应用的快速增长,网络拥塞越来越频繁。主动队列管理(active queue management,AQM))成为拥塞控制的研究热点。文献[1]对TCP网络的非线性动态模型进行了线性化处理后得到了一个线性定常TCP网络模型,并分析了随机早期丢弃(random early discard,RED)算法不稳定的原因。然而依据该模型设计的AQM控制器[2]在鲁棒性方面遇到了一些困难,因为TCP网络的高度变化使得网络参数很难长时间保持在常值。对于时变TCP网络而言,由于滑模控制系统中的滑动模态与系统的摄动和外界干扰无关[3],因此滑模控制在TCP网络拥塞避免方面取得了较好的效果[4]。但以上文献只适用于线性系统模型。文献[5]基于非线性TCP网络动态模型[6]设计了一种滑模控制器,增强了系统的鲁棒性,但是这类控制器要求TCP负载和往返时延的界必须事先获得。然而在实际应用中,由于TCP负载和往返时延具有较大突发性和时变性,它们的界很难确定,从而造成控制器在实际中很难实现。文献[7]利用拥塞窗口和往返时延信息设计了一种非线性主动队列管理控制器,但是由于拥塞窗口信息在路由器端很难获得,使得控制器在实际应用中很难实现。
径向基函数(radial basis function,RBF)神经网络具有良好的非线性逼近能力[8],若将滑模控制与RBF神经网络相结合设计控制器,则能进一步提高控制效果。近年来,在电力系统和电机磁链等领域取得了一些较好的成果[9-10],但在TCP网络的拥塞控制方面则鲜有报道。
本文首先将TCP网络的非线性动态模型转换成仿射非线性形式。然后基于滑模变结构的控制理论设计了一个滑模控制器。然而由于TCP负载和往返时延具有较大突发性和时变性,使得网络系统参数是未知时变的,从而导致滑模控制器在实际应用中很难实现。为此,本文使用RBF神经网络逼近网络系统参数,依据李雅普诺夫理论设计了RBF神经网络权值的自适应律,采用RBF神经网络的输出作为滑模控制器的参数,从而使得滑模控制器易于实现。
1 TCP网络非线性动态模型
文献[6]采用基于速率的流体流分析方法,给出了TCP网络非线性动态模型为
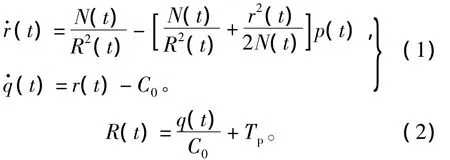
式中:r(t)为TCP连接的源端发送速率;q(t)为瞬时队列长度;N(t)为TCP网络的负载;R(t)为往返时延;Tp为传播时延;C0为链路带宽;0≤p(t)≤1为分组丢弃/标记概率,可以看作用于调节发送速率和链路队列长度的控制输入。
令eq=q(t)-qd,qd为期望的队列长度。记x1=eq,x2=,则有
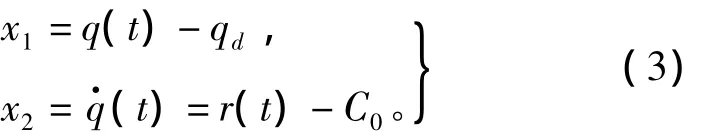
于是非线性模型(1)可表示为
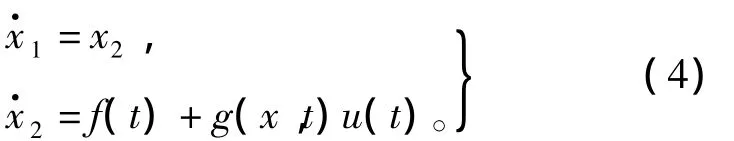
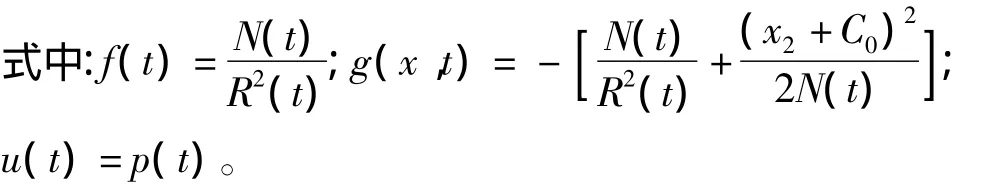
2 自适应神经滑模控制
2.1 滑模控制器设计
滑模变结构控制器的设计由两部分组成。首先,设计具有良好的动态特性的滑动模面为
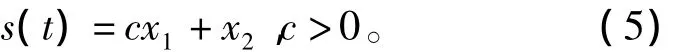
接着,设计使滑动模态存在的滑模控制器u(t),为
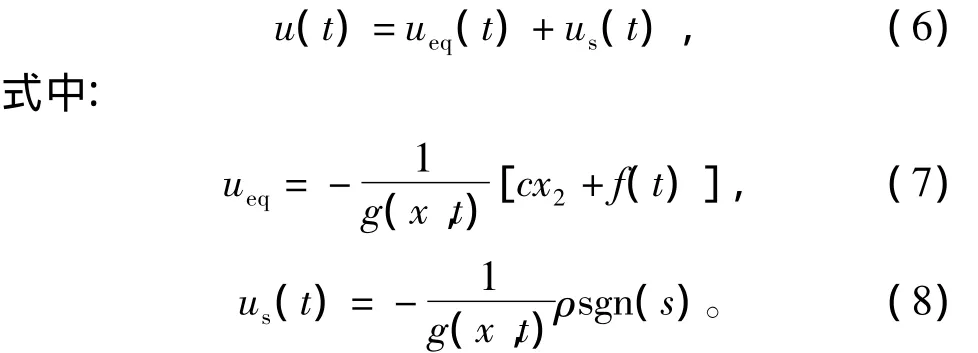
其中:ueq为滑模等效控制;us(t)为切换控制,用于实现对网络系统的摄动和外加干扰的鲁棒控制;ρ>0是切换增益。
定理1 系统(4)在控制律(6)、(7)和(8)的作用下能在有限时间内到达滑动模面,并保证滑动模面是渐近稳定的,即使滑动模态存在条件<0成立。
证明:选取Lyapunov函数如下
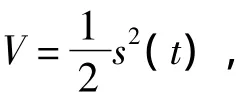
于是,对V关于时间t求导,得到
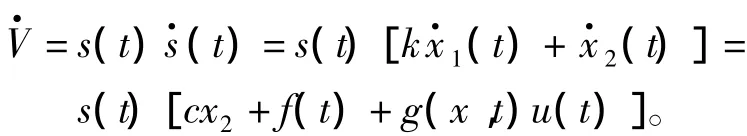
将式(6)、式(7)和式(8)代入,得到
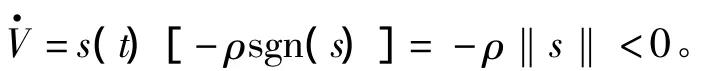
当t→∞时,s(t)→0,滑动模面s(t)=0总能在有限时间内到达,而且是渐近稳定的。
2.2 自适应神经滑模控制器设计
在实际应用中,由于TCP负载N(t)和往返时延R(t)具有较大突发性和时变性,所以f(t)和g(x,t)是未知时变的,控制器很难实现。可采用RBF网络的输出(t)和(x,t)代替f(t)和g(x,t),实现自适应神经滑模控制。
RBF神经网络具有如下形式,即

式中:y(x,ω)是神经 RBF 网络的输出;x=[x1,x2]是输入状态向量;ω∈Rn是RBF神经网络的权向量;向量φ(x)∈Rn是高斯型函数,其形式为
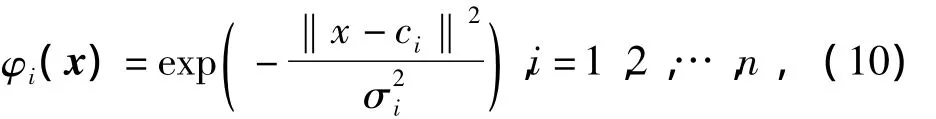
式中:ci∈R2n是第i个神经元的中心位置;σi∈R是第i个神经元的宽度。
采用RBF网络建立(t)和(x,t)的模型,网络结构如图1所示。
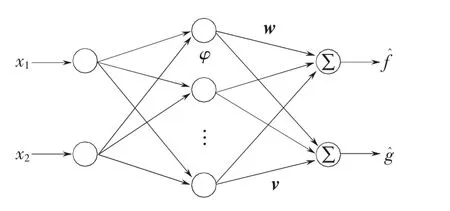
图1 RBF网络结构Fig.1 RBF network structure
为了进一步分析,引进如下假设:
假设1 对于任意给定的逼近精度ε,存在权向量w和v,使得和分别逼近于f和g,即存在权向量w和v,使得
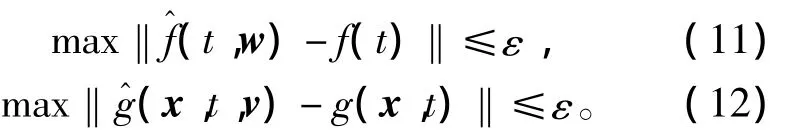
成立。
令wt和vt分别表示权向量w和v在t时刻的估计值,控制律(7)和(8)改写为

式中:
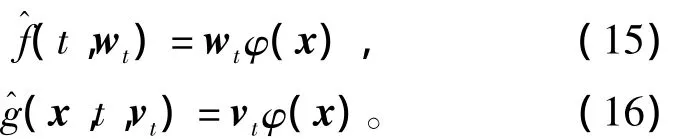
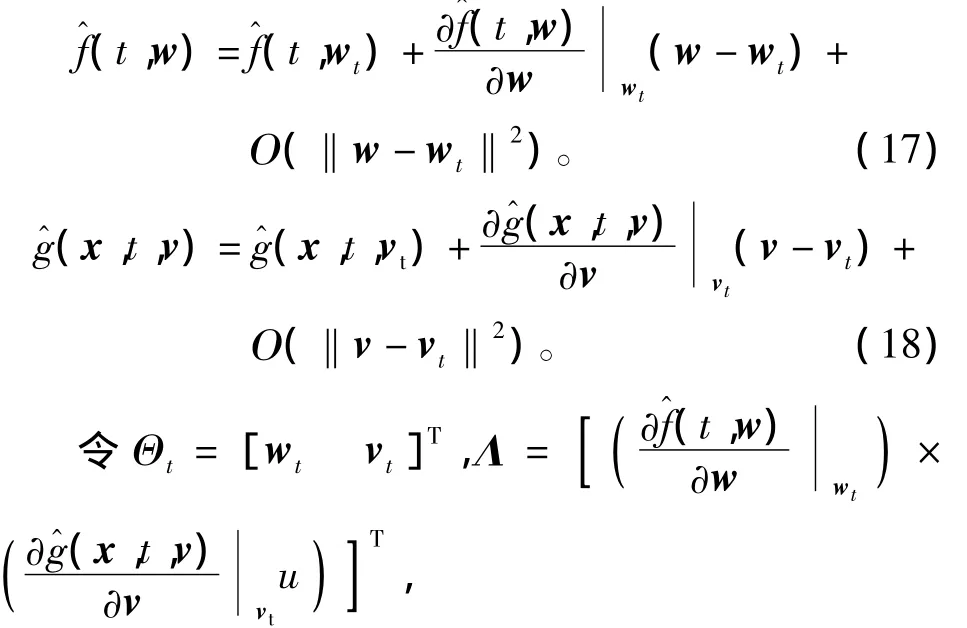
由中值定理可以得到
则RBF网络的权值采取自适应机制在线调整为

令Θ=[wv]T,则 RBF网络的权值误差为(t)=Θt-Θ,逼近误差为η(t)=Ο(‖(t)‖2)+Ο(ε)。
定理2 如果假设1成立,且满足ρ(t)>‖η(t)‖,则系统(4)在控制律(6)、(13)和(14)以及自适应律(19)的作用下能在有限时间内到达滑动模面,并保证滑动模面是渐近稳定的。
证明:考虑如下李雅普诺夫函数:
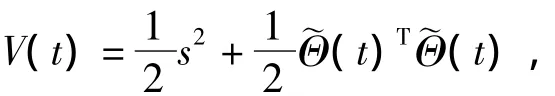

将控制律(6)、(13)和(14)代入得到
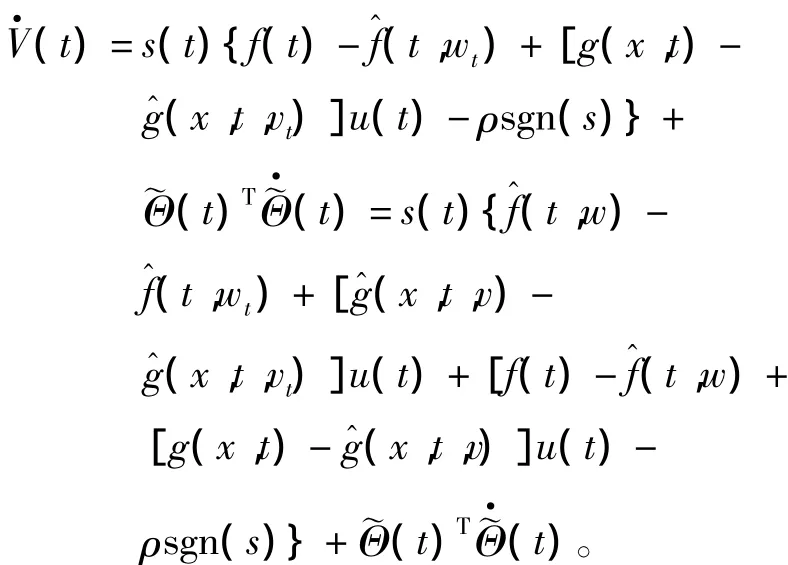
由假设1以及式(17)、式(18)和式(19)得到
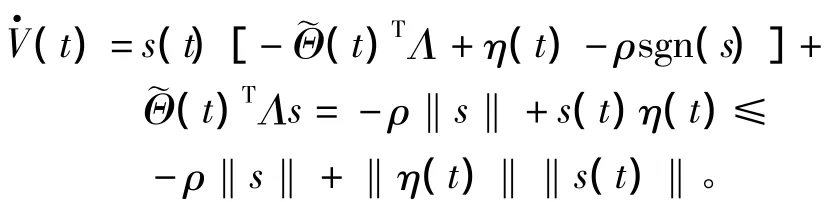
当选择滑模切换增益ρ(t)>‖η(t)‖时,

当t→∞时,s(t)→0,滑动模面s(t)=0总能在有限时间内到达,而且是渐近稳定的。
3 仿真研究
参照文献[1],网络参数的选择为,N=100,C0=1 250 分组/s,R=0.2 s,qd=100 分组。滑模面控制参数c=10,切换增益ρ=10。神经元的中心ci在0和1之间随机取值,神经元的宽度σi都取1。为了便于性能分析,本文对文献[2]提出的比例积分(proportional-integral,PI)控制器和文献[5]提出的滑模控制(sliding mode control,SMC)与本文的神经滑模控制器(neural sliding mode control,NSMC)进行了仿真,仿真结果如图2~图5所示。
从图2可以看出,当网络参数确定时,PI控制器、SMC控制器和NSMC控制器都能使瞬时队列长度稳定在期望值附近。但是PI控制器产生的波动较大,收敛时间也比较长;NSMC控制器和SMC控制器都具有较好的收敛性能,能较快地收敛到期望值附近。
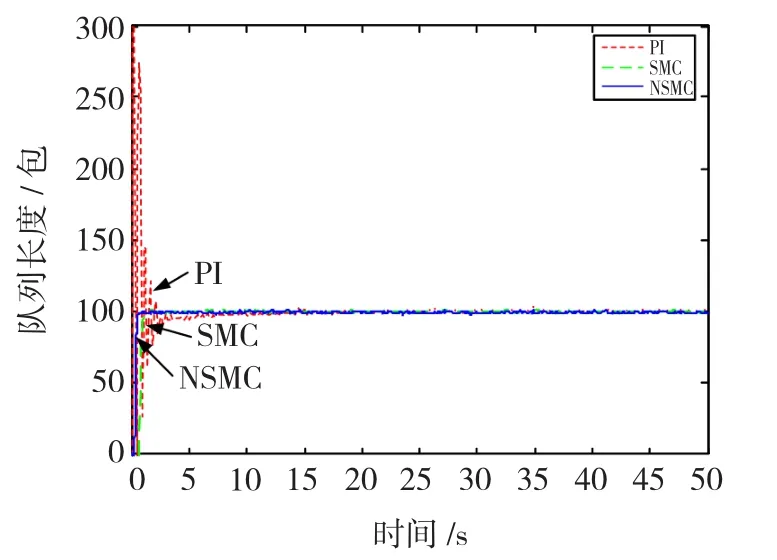
图2 网络参数确定时队列长度比较Fig.2 Comparison of queue lengths with fixed network parameters
从图3可以看出,当网络负载N从100变化到200,其它网络参数不变时,PI控制器显示出较大的稳态误差和较慢的暂态响应;SMC与NSMC相比,在稳态过程中队列长度变化有较大幅度振荡。
当往返时延R从0.2 s变化到0.3 s,其它网络参数不变时的仿真结果如图4所示。PI控制器经过较大地振荡之后能够收敛于期望值,而且在稳态过程中,队列长度变化比较剧烈;NSMC同SMC相比,能使队列长度很快收敛于期望值,并且稳态时的队列长度变化较小而且平缓。
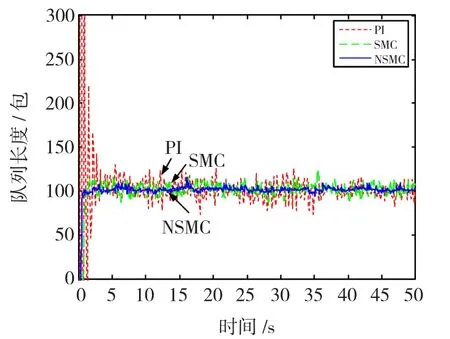
图3 较大TCP负载时队列长度比较Fig.3 Comparison under higher TCP loads
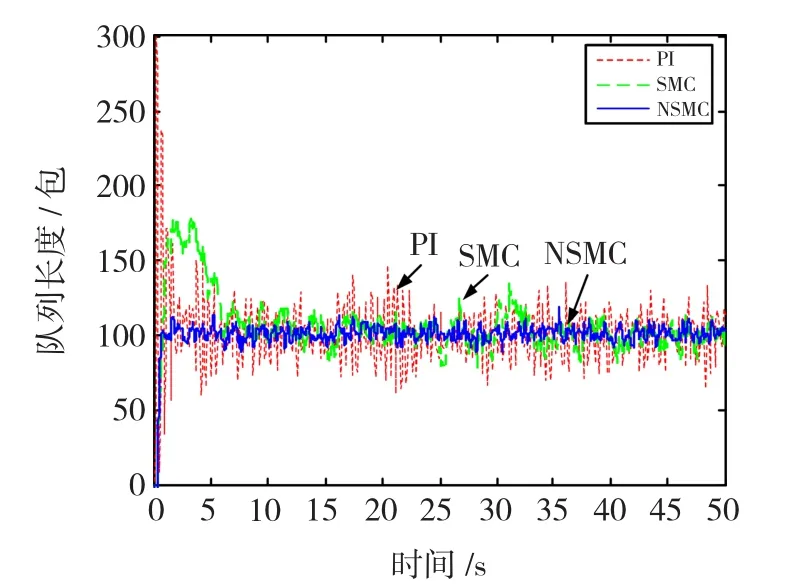
图4 较大往返时延时队列长度比较Fig.4 Comparison with larger round-trip time
当往返时延R从0.2 s变化到0.3 s,网络负载N从100变化到200时,仿真结果如图5所示。PI控制器的收敛速度较慢,队列长度波动较大;SMC控制器在开始时队列长度变化比较剧烈,而NSMC控制器的队列长度变化比较平缓。
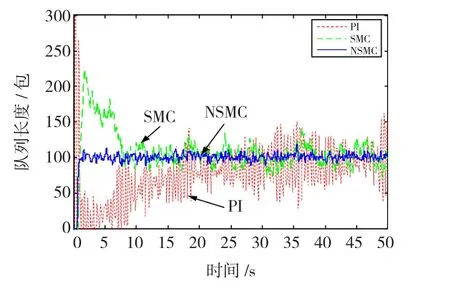
图5 网络参数变化时队列长度比较Fig.5 Comparison of queue lengths with variable network parameters
4 结论
针对TCP网络的拥塞控制问题,将滑模控制与RBF神经网络相结合设计了一种主动队列管理算法。该算法具有以下特点:
1)由于TCP负载和往返时延具有较大的突发性和时变性,使得网络系统参数是未知时变的。为此,使用RBF神经网络逼近网络系统参数,从而使得控制器易于实现。
2)基于李雅普诺夫稳定性理论设计了RBF神经网络权值的自适应律,使得网络系统参数得到了较好的估计,并且保证了网络系统的稳定性。
3)采用RBF神经网络的输出作为滑模控制器的参数设计了一种主动队列管理算法,使得系统状态能在有限时间内到达滑动模面,并保证滑动模面是渐近稳定的,而且瞬时队列长度具有较好的暂态和稳态性能。
本文设计控制器时,未考虑到无响应流对系统造成的影响,这将是下一步的研究工作。
[1]HOLLOT C,MISRA V,GONG W B.A control theoretic analysis of RED[C]//Proceedings of IEEE INFOCOM,April 22-26,2001,Anchorage,USA.2001:1510-1519.
[2]HOLLOT C,MISRA V,TOWSLEY D,et a1.On designing improved controllers for AQM routers supporting TCP flows[C]//Proceedings of the IEEE INFOCOM,April 22-26,2001,Anchorage,USA.2001:1726-1734.
[3]WANG S P,GAO W B.Robustness and invariance of variable structure systems with multiple inputs[C]//Proceedings of the A-merican Control Conference,June 21-23,1995,Seattle,USA.1995:1035-1039.
[4]REN F Y,LIN C,YING X H.Design a congestion controller based on sliding mode variable structure control[J].Computer Communications,2005,28(9):1050-1061.
[5]YAN P,GAO Y,ÖZBAY H.A variable structure control approach to active queue management for TCP with ECN[J].IEEE Transactions on Control Systems Technology,2005,13(2):203-215.
[6]KELLY F P.Mathematical modeling of the Internet[C]//Mathematics Unlimited-2001 and Beyond,January 25,2001,Berlin,Germany.2001:685-702.
[7]陈玮,王银河,井元伟,等.TCP网络主动队列管理的非线性状态反馈跟踪控制[J].电机与控制学报,2009,13(5):762-765.
CHEN Wei,WANG Yinhe,JING Yuanwei,et al.Nonlinear state feedback tracking control algorithm for active queue management of TCP network[J].Electric Machines and Control,2009,13(5):762-765.
[8]PARK J,SANDBERG I W.Universal approximation using radial basis function networks[J].Neural Computation,1991,3(2):246-257.
[9]徐庆宏,戴先中.基于在线学习RBF神经网络的汽门开度自适应补偿控制方法[J].电机与控制学报,2010,14(2):13-19.
XU Qinghong,DAI Xianzhong.Online learning RBF neural network-based adaptive compensative control scheme for governor system[J].Electric Machines and Control,2010,14(2):13-19.
[10]刘国荣,张道禄.电机磁链神经网络观测器的研究[J].电机与控制学报,2011,15(8):81-87.
LIU Guorong,ZHANG Daolu.A study of motor flux neural network observer[J].Electric Machines and Control,2011,15(8):81-87.

