转子磁链误差对感应电机观测器稳定性影响

许思猛， 陈冲

(1．福州大学电气工程与自动化学院，福建福州 350108;2．福建工程学院电子信息与电气工程系，福建福州 350108)

0 引言

自感应电动机无速度传感器控制技术出现以来，已取得了显著的进展，其中以全阶转速自适应转子磁链观测器［1－2］最受关注，至今仍是研究的热点。Kubota在文献［1］通过Lyapunov函数推导转速自适应律，G．Yang在文献［2］从Popov超稳定理论推导得到转速自适应律。由于直接测量转子磁链困难，在转速自适应机构中文献［1］将转子磁链误差忽略，文献［2］用励磁电感乘以定子电流误差代替。

该观测器在电机低速再生发电工况运行时可能不稳定［3－4］，为解决此问题文献［5 －7］提出了调节反馈增益的方法，文献［5］在旋转坐标系中将观测器在稳定点邻域线性化，应用Routh-Hurwitz稳定判据确定反馈增益。文献［6］通过反馈增益改变特征矩阵特征根分布完全消除不稳定区域。文献［7］则从满足前向通道传递函数严格正实条件来设计反馈增益。

文献［8－12］修正转速自适应律以解决上述稳定性问题。文献［8］改变定子电流误差矢量方向，文献［9］在自适应误差项中增加一补偿项以补偿忽略的转子磁链误差，文献［10］将定子电流误差矢量和转子磁链误差矢量的内积作为补偿项，文献［11］指出文献［8，10］在电动工况时可能不稳定，文献［12］从分析线性化的前向通道反馈矩阵特征值出发，分析了文献［8，10，11］提出的转速自适应律结论，指出文献［9］方法与文献［8，10］是一致的。

可以认为改变转速自适应律实际上是在经典观测器的转速自适应律中加入一补偿项，该补偿项是用于替代无法直接获得的转子磁链误差，因此在进行补偿之前有必要对转子磁链误差的作用进行分析。有文献［8］认为观测器不稳定的根本原因是忽略了转子磁链误差，但并没有进行严格推导。

改变转速自适应律的目的是在观测器开环条件下也能保证稳定，因此在提高观测器鲁棒性设计方面比调节反馈增益方法更灵活［12－13］。观测器对模型参数非常敏感［14］，模型参数的变化不仅影响观测器的性能，甚至会导致不稳定，如果稳定性能够由自适应律来满足，则可将反馈增益主要用于鲁棒性能设计。

本文从等效误差方程推导转子磁链误差模型，从前向通道传递函数正实性［15］和等效转速控制系统的开环零点分布两个方面，分析转子磁链误差对观测器稳定性的影响。为避免在转子磁链误差模型中含纯积分器，给出一个近似的转子磁链误差模型，分析采用该转速自适应律时观测器的稳定性，最后利用MATLAB对观测器进行仿真。

1 全阶自适应转子磁链观测器

在静止dq坐标系下，经典的感应电动机状态观测器由可直接测量的定子电流观测误差来构成校正项，为［1－2］

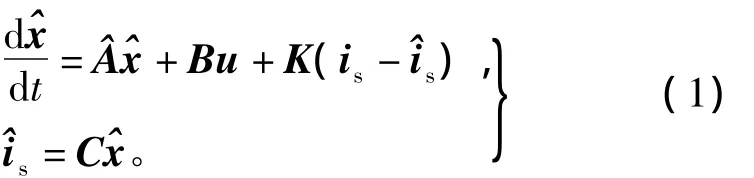
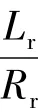
定义广义状态误差为

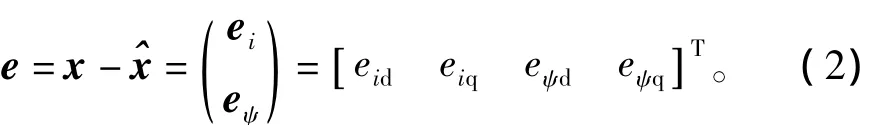
得到等效的动态误差方程为

根据Popov超稳定理论，推得转速自适应律［2］为

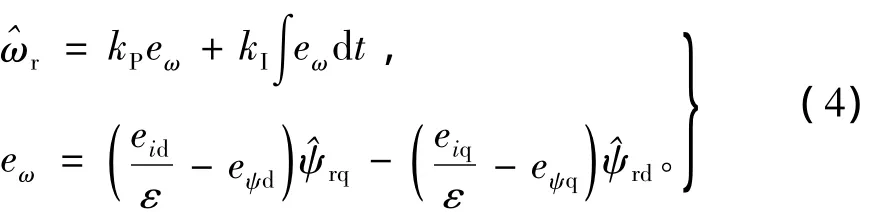
其中kP、kI为自适应机构比例与积分系数。根据转子磁链电压矢量方程

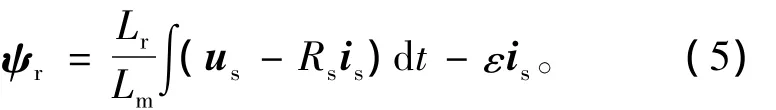
得到转子磁链误差矢量表达式为

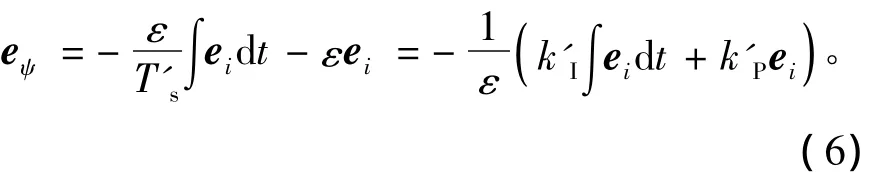
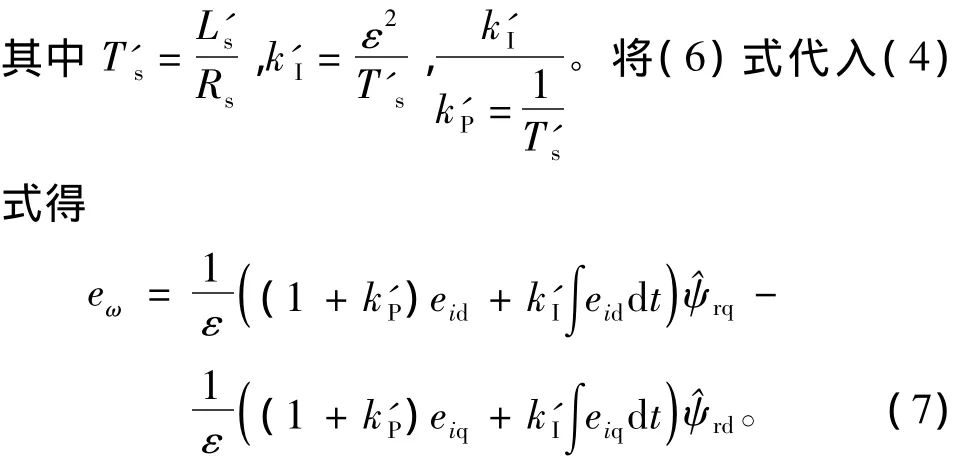
由此得到包含完整转子磁链误差信息的全阶转速自适应转子磁链观测器，如图1所示。

图1 全阶自适应观测器的等效误差系统原理图Fig．1 Schematic diagram of the equivalent error system of the full-order adaptive observer

2 转子磁链误差对观测器稳定性影响

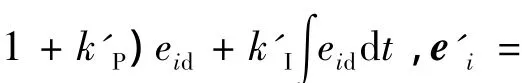
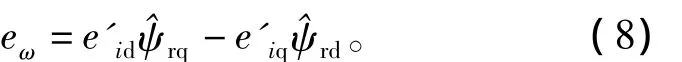
根据式(8)将图(1)简化后得到图2。

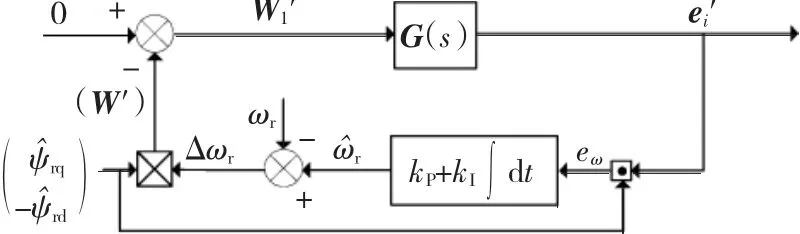
图2 简化的等效误差系统原理图Fig．2 Schematic diagram of the symplified equivalent error system

图2表明增加转子磁链误差后只改变等效误差系统前向通道传递函数，对反馈通道并无影响，根据Popov超稳定理论，此时观测器稳定性取决于前向通道传递函数矩阵G(s)的严格正实性，即

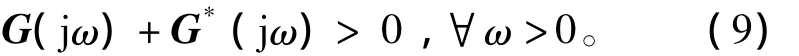
式中(*)表示共轭转置。根据(9)式得到观测器在ω1－ωs平面中的稳定区域边界线的方程为

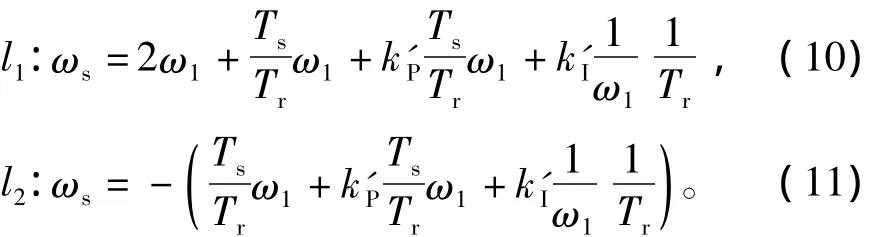
式中:ωs为转差速度;ω1为同步速。加入eψ后观测器稳定区域分布如图3(a)所示。为了便于读图，图中横坐标单位用频率Hz，纵坐标单位用速度r/min。由于原点附近的稳定区域很小，图中用直线近似l1和l2。当k'p=k'I=0时，相当于忽略了eψ。可以看出在加入eψ之后，稳定区域扩大量Δωs非常小，如图3(b)所示。在低速时，扩大稳定区域主要依赖于式(6)中的对ei的积分项，由于k'I中含参数ε2，降低了1/ω1对扩大稳定区域的作用。如果放大转子磁链误差1/ε2倍，则能显著扩大稳定区域，如图3(c)所示。图中分析所采用电机参数为:PN=2.2 kW，UN=220 V，fN=60 Hz，nN=1725 r/min，Rs=0.435 Ω，Rr=0.816，Lm=69.31 mH，Ls=Lr=71.31 mH。

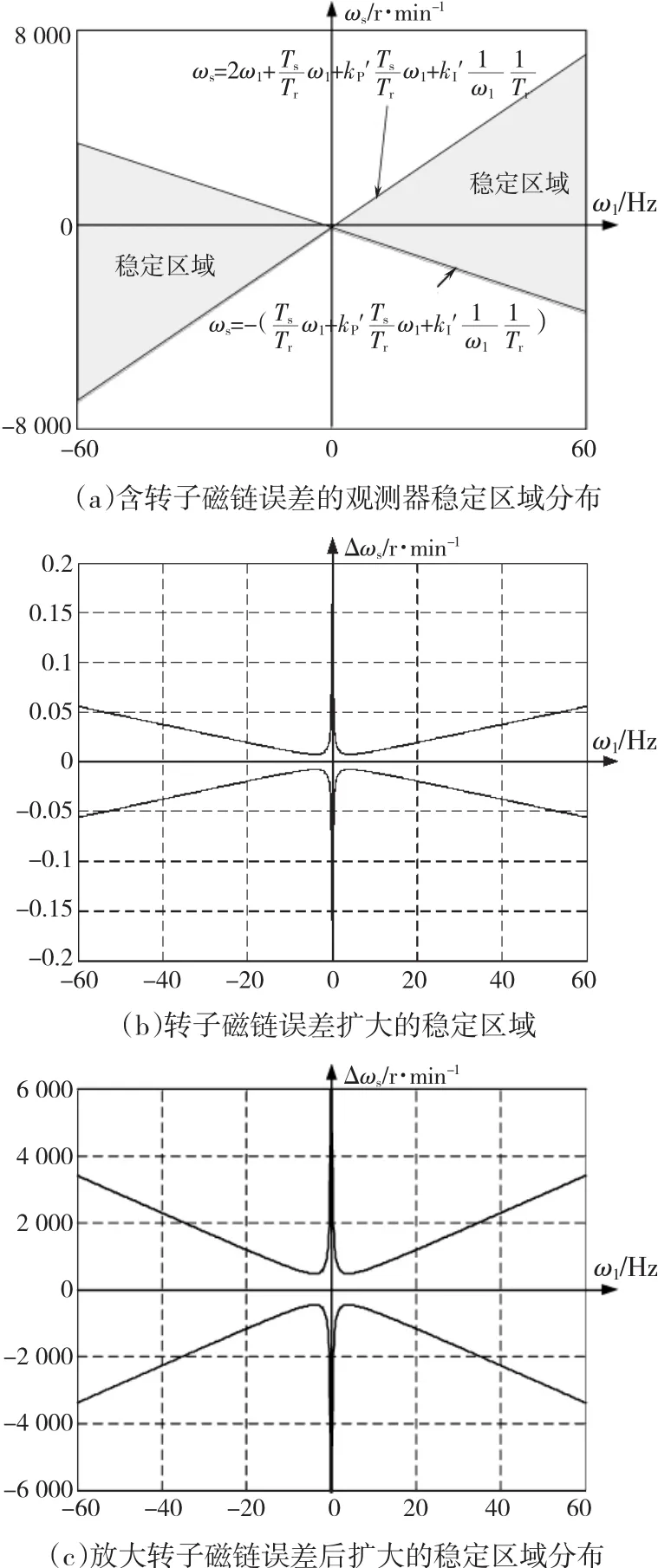
图3 观测器在ω1－ωs平面上稳定区域分布Fig．3 Observer stable region distribution in ω1－ωsplane

转速自适应观测器中的转速估计系统可以看作是一个转速闭环控制系统，将系统变换到同步坐标系后在稳定点(ω10，ωr0，ψr0)进行微偏线性化，得到如图4所示的动态系统框图。

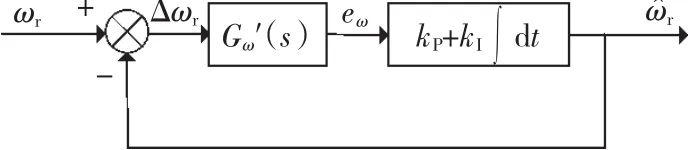
图4 线性化后的等效转速闭环控制系统框图Fig．4 Linearized equivalent close loop speed control system

实际转速为给定转速，估计转速为输出，传递函数G'ω(s)特性由电机本身决定，表达式如式(12)。它的输入除了转速偏差外，还有定子电压和频率信号(图中未标出)，输出eω作为转速自适应机构的输入。

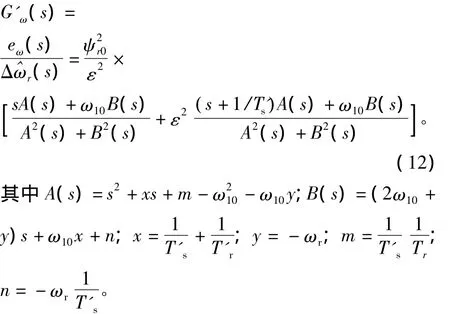
由控制理论得知，图4中的转速闭环控制系统稳定时，其闭环极点必须全部位于s平面的左边。由于转速自适应机构在原点有一个开环极点，为避免在右半平面出现闭环极点，G'ω(s)所有的开环零、极点必须全部位于s平面的左半平面。G'ω(s)的零点由式(13)确定:

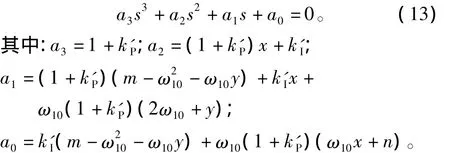
根据 Routh-Hurwitz稳定判据，G'ω(s)所有的零全部位于s左半平面的条件为

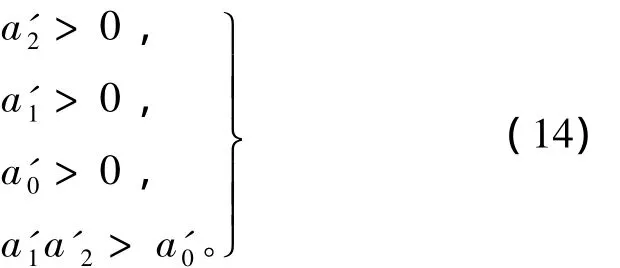
则可以在ω1－ωs平面上确定出等效闭环转速控制系统的稳定区域如图5，图中黑色区域表示系统不稳定，白色表示系统稳定。

图5表明虽然在转速自适应律中包含了转子磁链误差，但在低速再生发电工况时，观测器不能稳定。当扩大转子磁链误差，则能够将稳定区域扩大到整个ω1－ωs平面。

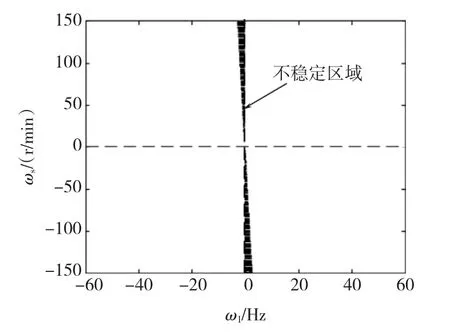
图5 转速估计系统不稳定区域分布Fig．5 Unstable region of close loop speed control system

应用正性系统理论与经典控制理论分析均表明:当观测器开环时，为了使全阶转速自适应转子磁链观测器稳定，需放大转子磁链误差。在第3节推导新型转速自适应律时将用到这一结论。

3 新型转速自适应律

由于在式(6)中含纯积分器，直接应用该式求转子磁链误差实际中难以实现，本文给出转子磁链误差的近似表达式为

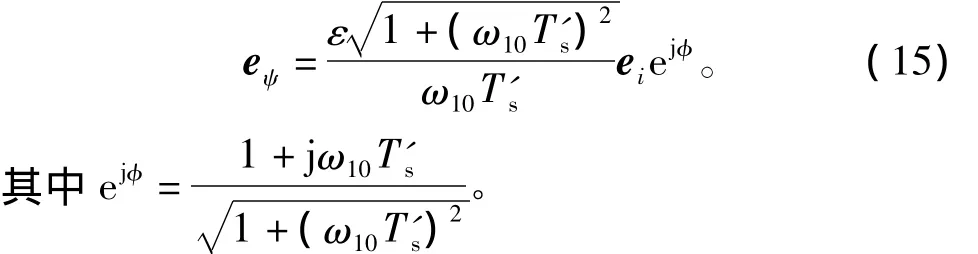
应用已得到的结论，将eψ放大1/ε2倍后代入式(4)，得到的转速自适应误差为

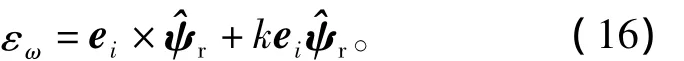
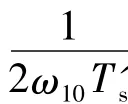
式(16)与文献［9］给出的转速自适应律类似，文献［9］的稳定区域分布如图7，观测器只在高定子频率电动工况时不稳定，因此可以选择:

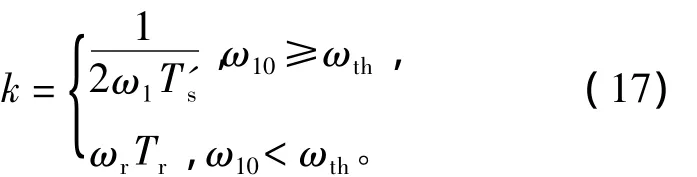
式中ωth为两个转速自适应律切换阀值，从图6和图7中可看出，ωth的取值范围很大，采用式(17)的转速自适应律在电动工况时无需令k=0，因此为在整个ω1－ωs平面中进行观测器设计增加了一个自由度。

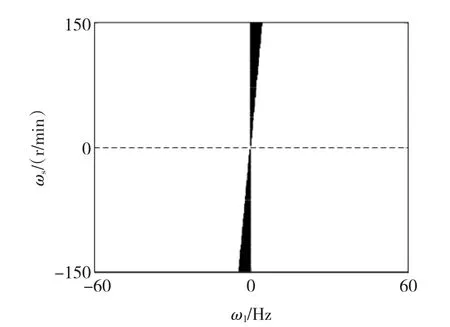
图6 新型转速估计系统不稳定区域分布Fig．6 Unstable region of novel close loop speed control system

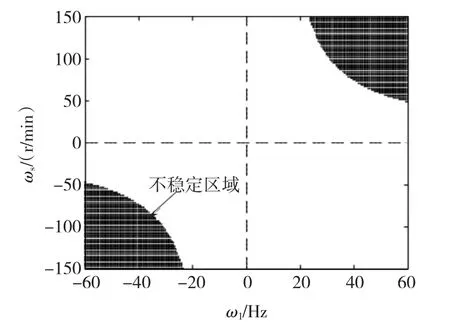
图7 其它转速估计系统不稳定区域分布Fig．7 Unstable region of other close loop speed control system

4 仿真及结果分析

由于实际验证转子磁链误差对观测器稳定性影响困难，此时应用仿真是合适的手段。系统平台采用Matlab中的矢量控制系统AC3，转速自适应机构参数kP=0.01，kI=20 000。

图8为未忽略转子磁链误差时观测器仿真波形，图8(a)为负载转矩TL波形，负载转矩在0～0.5 s期间为11 N·m，然后突变为－6 N·m，电机由电动进入再生发电工况。图8(b)中给定转速为100 r/min，观测器输出转速^ωr在电机进入再生发电工况后偏离实际转速，说明观测器此时不能稳定运行。

图9本文提出的新型转速自适应律观测器转速输出仿真波形，图9(a)与图8(a)相同。图9(b)中给定转速在1 s处由100 r/min变化到－100 r/min，运行至1.5 s再变化到100 r/min，电机工况由正向电动运行，变化到正向再生发电运行，再进入反向电动运行，最后回到正向再生发电运行，仿真结果说明观测器此时能够稳定运行。

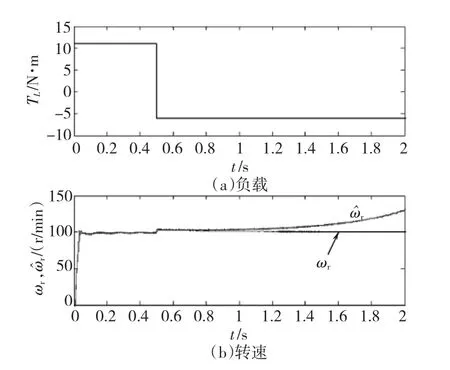
图8 未忽略转子磁链误差观测器仿真波形Fig．8 Simulation waveform of the observer without neglecting the rotor flux error

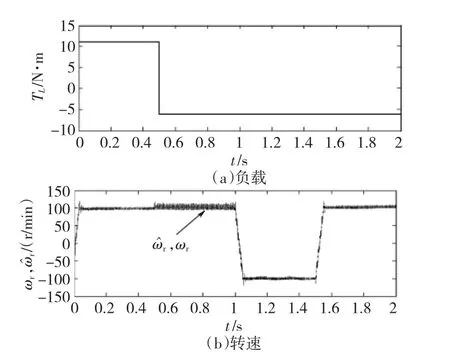
图9 新型转速自适应律观测器仿真波形Fig．9 Simulation waveform of the observer with novel speed adaptation law

5 结论

将转速自适应律中的转子磁链误差项放大，能够满足全阶转速自适应转子磁链观测器等效误差系统前向通道传递函数是严格正实的。基于转子磁链误差近似模型的改进转速自适应律能够保证低速再生发电工况时观测器是稳定的，但在电动工况时存在不稳定区域，组合应用不同的转速自适应律能够为观测器设计增加一个自由度。本文针对不同转速自适应律给出的稳定区域分布是在观测器反馈增益矩阵为零条件下得到的，后续工作将对反馈增益矩阵对稳定区域分布区域分布影响进行研究。

［1］KUBOTA H，MASTSUSE K，NAKANO T．DSP-based speed adaptive flux observer of induction motor［J］．IEEE Transactions on Industry Applications，1993，29(2):344 －348．

［2］YANG G，CHIN T H．Adaptive-speed identification scheme for a vector-controlled speed sensorless inverter－induction motor drive［J］．IEEE Transactions on Industry Applications，1993，29(4):820－825．

［3］HOFFMANN H，SANDERS S．Speed-sensorless vector torque control of induction machines using a two-time-scale approach［J］．IEEE Transactions on Industry Applications，1998，34(1):169－177．

［4］李永东，曾毅，谭卓辉，等．无速度传感器三电平逆变器异步电动机直接转矩控制系统(II)—基于全阶定子磁链观测器的参数和速度辨识［J］．电工技术学报，2004，19(8):88－92．

LI Yongdong，ZENG Y，TAN Zhuohui，et al．Sensorless direct torque control of induction motor fed by three level inverter(II)—parameters and speed identification based on full order stator flux observer［J］．Transactions of China Electrotechnical Society，2004，19(8):88－92．

［5］KUBOTA H，SATO L，TAMURA Y，et al．Stable operation of adaptive observer based sensorless induction motor drives in regenerating mode at low speeds［C］//Industry Applications Conference，2001．Thirty-Sixth IAS Annual Meeting．Conference Record of the 2001 IEEE，September 30 － October 4，2001，Chicago，USA．2001(1):469－474．

［6］BENSIALI N，CHAIGN C，ETIEN E．Optimal observer design for sensorless control of induction motor in regenerating－mode［C］//IEEE International Symposium on Power Electronics，Electrical Drives，Automation and Motion，May 23 －26，2006．Taormina，Italy:2006．

［7］SUWANKAWIN S，SANGWONGWANICH S．A speed-sensorless IM drive with decoupling control and stability analysis of speed estimation［J］．IEEE Transactions on Industrial Electronics，2002，49(2):444－455．

［8］HOFFMANN F，KOCH S．Staty state analysis of speed sensorless control of induction machines［C］//Proceedings of the 24th Annual Conference of the IEEE Industrial Electronic Sosiety，Aug 31－Sep 4，1998，Aachen，Germany．1998:1626－1631．

［9］TAJIMA H，GUIDI G，UMIDA H．Consideration about problems and solutions of speed estimation method and parameter tuning for speed-sensorless vector control of induction motor drives［J］．IEEE Transactions on Industrial Electronics，2002，38(5):1286－1289．

［10］RASHED M，STRONACH F，VAS P．A stable MRAS-based sensorless vector control induction motor drive at low speeds［C］//IEEE International Electric Machines and Drives Conference，June 1－4，2003，Madison，USA．2003:139－144．

［11］HINKKANEN M，LUOMI J．Stabilization of regenerating-mode operation in sensorless induction motor drives by full-order flux observer design［J］．IEEE Transactions on Industrial Electronics，2004，51(6):1318 －1328．

［12］ETIEN E，CHAIGNE C，BENSIALI N．On the stability of full adaptive observer for induction motor in regenerating mode［J］．IEEE Transactions on Industrial Electronics，2010，57(3):1599－1608．

［13］HINKKANEN M．Analysis and design of full-order flux observers for sensorless induction motors［J］．IEEE Transactions on Industrial Electronics，2004，51(5):1033 －1040．

［14］JANSEN P L，LORENZ R D．A physically insightful approach to the design and accuracy assessment of flux observers for field oriented induction machinedrives［J］．IEEE Transactions on Industry Applications，1994，30(1):101 －110．

［15］SANGWONGWANICH S，SUWANKAWIN S，PO-ngam S．et al．A unified speed estimation design framework for sensorless AC motor drives based on positiv-real property［C］//IEEE Power Conversion Conference，April 2 － 5 2007，Nagoya，Japan．2007:1111－1118．