单相有源PFC开环控制的研究

江剑峰 杨喜军 蒋婷 曹中圣

（上海交通大学 电气工程系电力传输与功率变换控制教育部重点实验室，上海 200240）

0 引言

为降低电网谐波污染、保护电力设备安全，包括空调、冰箱在内的许多变频家电、通讯电源、照明电器等都需要采用一些新型电路拓扑、控制原理或者滤波技术，以保证网侧谐波电流符合标准［1－4］。有源功率因数校正技术（Power Factor Correction，PFC）可以使电器设备负载特性为纯电阻特性，降低了网侧电流谐波的同时，也提高了电器效率，减少了损耗。目前PFC控制方法有双环控制［5］、电压跟随控制［6］、单周控制［7］、直接控制［8］以及无需输出电压检测的开环控制［9－11］等，均可以归类于开环控制和闭环控制。采用传统闭环控制算法PFC的控制量为输入电流与输出电压，为了获得稳定的输出电压同时使输入电流与输入电压相位一致，需要设计相应的电压外环和电流内环。这种控制方法需要检查输入电压瞬时值、电感电流瞬时值与输出直流电压瞬时值，检测量过多，调试不便。而开环或者只采用部分闭环的控制方法可以一定程度上减少检测电量、实现方便简单，并且也能够实现理想的校正效果和稳定电压输出。对一种无需输出电压检测的PFC作了理论分析和研究，采用只需检测整流桥后正弦半波电压和输出阻抗的纯开环控制策略，无需检测电感电流瞬时值，在仿真分析后，基于DSP TMS320F28335实现了一种单相数字PFC，并进行了实验验证。

1 有源PFC的开环控制原理

1.1 开环调制的工作原理

单相有桥PFC功率拓扑如图1所示，主要由网侧滤波电容C1、二极管整流桥 B1、升压电路（L1、S1、D1）和输出滤波电容 E1组成。其中，L1为升压电感，S1为斩波IGBT，D1为反向快速恢复二极管。忽略升压电感内阻、整流桥压降、二极管压降以及斩波IGBT的压降。

假定交流输入电压方程为:

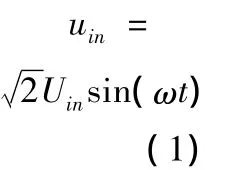
图1 单级有桥PFC功率电路

式中，Uin为交流输入电压有效值。

为简化分析，假定得到的交流输入电流为纯正弦波，其方程为:

式中，Iin为交流输入电流有效值。

设占空比函数为d，由图1，可得电感电压的表达式［9－11］为:

忽略二极管整流桥的导通压降，由式3，在［0，π］区间内，可得:

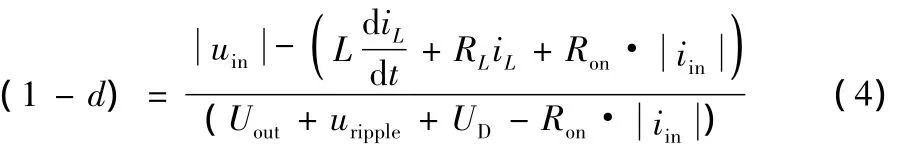
将式1、2代入式4，化简得:

Term1中，分式的分母中出现了输出纹波电压、二极管压降、IGBT压降。输出纹波电压的表达式为:

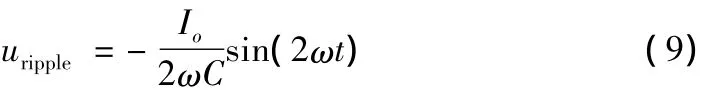
该纹波为正弦函数，其幅值与负载电流Io、电解电容容值、输入电压角频率有关。二极管压降与IGBT压降均为电流的非线性函数，均为正值。分式的取值受到这三个量的影响。鉴于Uout为参考电压，其数值远远大于这三个量的代数运算，因此可以忽略这三个量。

引入电压控制量k=Uout/Uin。基于以上考虑，Term1可以重写为:

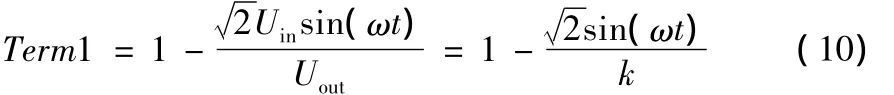
Term1中，分式的分子实际为整流后的电压，应该考虑整流二极管死区问题，同时需要考虑两只二极管的压降，该压降为电流的非线性函数，因此严格来说，分子应该增加一个可变的分量，以便补偿两只二极管的压降。粗略认为一个二极管的压降为UD。基于以上考虑，实际使用时，Term1可以改重写为:

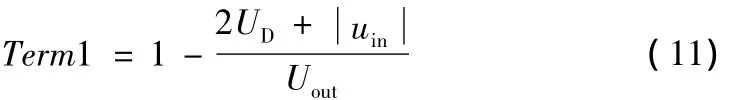
经过分析，Term1在占空比表达式中起着主要作用，称为电压平衡分量［12］，定义为电压占空比，代表输出电压给定值，与输出功率无关，波形为倒正弦波，与输入交流电压相位相反。只能维持空载输出电压。Term1中没有考虑到占空比随输入电压波形、输出功率和电感能量的变化。

Term2中，分式的分母同样出现了输出波电压纹、二极管压降与IGBT压降，这三部分的代数运算远远小于Uout，因此可以忽略。假定PFC的效率为100%，则由功率平衡条件可得输入电流有效值为:

式中，Zout为负载等效电阻。

Term2可以重写为:

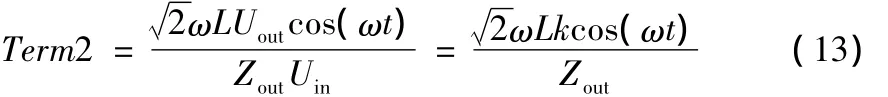
Term2中，分式的分子实际为电感电流的微分。经过分析，Term2在占空比表达式中起着重要作用，称为电流强迫分量，定义为功率占空比，其波形与电感电流有关，为电感电流的导数，与电感电流的电能储存与释放有关，其幅值与输出功率有关。空载时，Term2=0。输出功率越大，等效输出阻抗越小，附加占空比所占比重增加。

显然，对于纯直流输入－直流输出的DC－DC变换器，不存在附加占空比问题。

Term3中，分式的分母同样出现了输出电压纹波、二极管压降、IGBT压降，这三部分的代数运算远远小于Uout，因此可以忽略。Term3重写为:

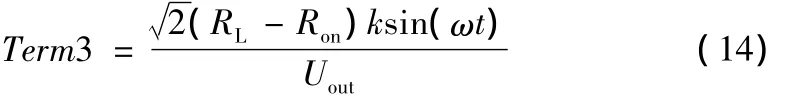
Term3可以看作扰动量，称为附加占空比，按照正弦波规律变化，与输出功率大小有关，其极性与IGBT导通阻抗与电感分布电阻的大小有关，一半为负极性。重载时，Term3需要进行补偿。

综合以上，有源PFC的占空比函数如图2所示，可见最终占空比函数为周期函数，在［0，π］内呈现不对称，而且出现一个占空比函数大于1的死区。考虑到有源PFC为升压DC-DC变换器，占空比最大值一般不大于0.95，这样实际应用中占空比函数的死区将更大。输出功率越大，死区越大。ωL/Zout比值越大，死区越大。死区的存在将影响PFC的校正效果。可以令d=dmax，求解超越方程，得到死区长度。

在［0，π］区间内，可得简化后的占空比函数。

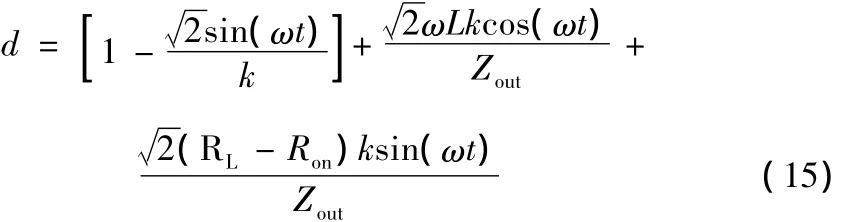
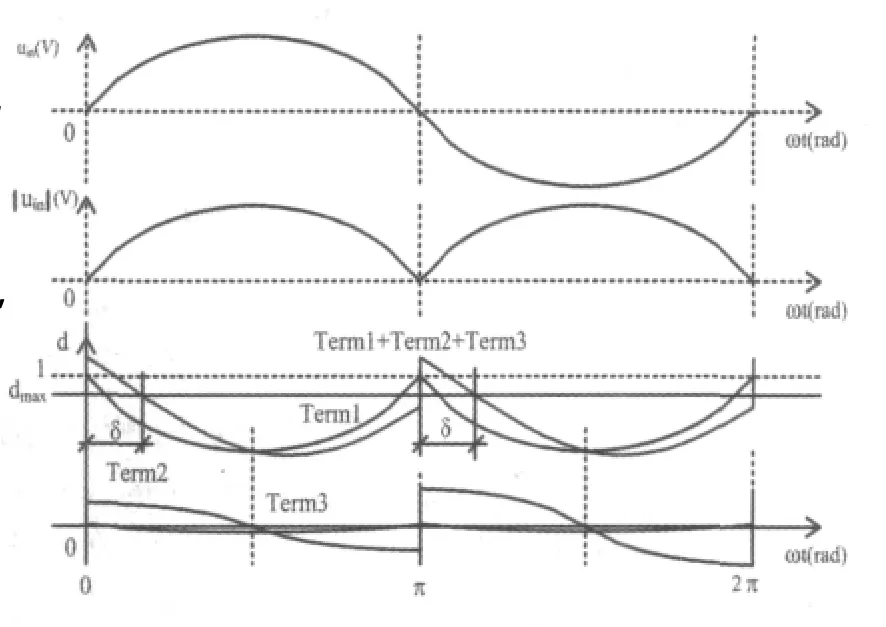
图2 有源PFC占空比函数的合成

由式（15）可知，如果PFC中电感量、电网电压角频率、电压控制量k一定时，只需知道负载阻抗，就可以实现功率因数校正，而无需检测电感电流瞬时值，同时基本占空比和输出电压与输出功率无关。

保持k不变，就可以实现输出电压相对输入电压的跟随特性，由此可以简化低压输入条件下电感设计，降低成本。

由式（15）还可知，只需要检测整流桥后正弦半波电压，实时计算输入电压角频率和有效值，就可以实现开环控制策略。

但是可以发现，式（15）中要求实时计算输出阻抗，否则上述有源PFC没有实际应用价值。

1.2 开环调制的设计方案

根据式（15），只要知道给定k和实测测算负载阻抗Zout以及获得输入电压波形，就可以实时计算有源PFC的占空比。为此可以获得多种设计方案，文中采用以下设计方案，如图3所示。

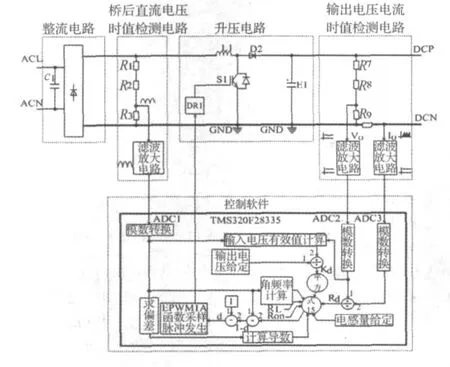
图3 单级有源PFC开环控制设计方案

图3中由功率电路和控制电路构成，前者包括整流电路、桥后直流电压时值检测电路、升压电路和输出直流电压电流时值检测电路。实时测量桥后电压时值，计算输入交流电压有效值和频率，并用于交流电源过压与欠压保护;实时测量载侧电压与电流时值，计算负载阻抗，并用于输出过压、欠压、开路保护以及输出过流、过载保护。

后者主要包括数字控制软件部分，将检测的相关信号经过滤波和模数转换后，利用式（15）进行标定和计算。DSP TMS320F28335支持浮点运算，可以大大简化运算程序。关于式（15）中的第二项，涉及对输入电压的求导，一种简便的计算方法为:将桥后直流电压的相邻两次采样的差值除以采样周期与角频率的乘积（即开关周期），即可得到式（15）中的第二项。计算公式如下:

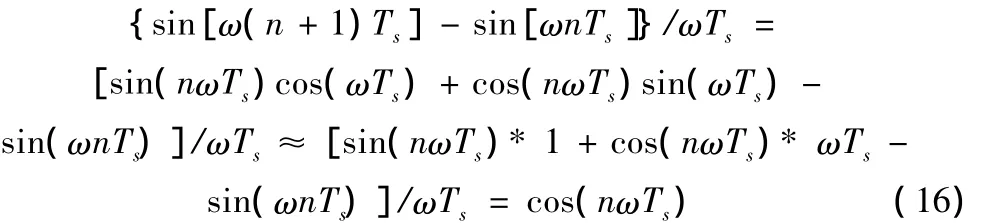
式中，Ts指开关周期或采样周期。

对于两级交错有源PFC，由式（15）可知，每级PFC的电压占空比不变。当采用同一控制器时，两级交错载波相差180°，每个电感电流瞬时值为总电流瞬时值的一半，相当于负载阻抗增加一倍，因此功率占空比应该减半处理。

开环控制的两级有源PFC，由于没有采取均流措施，需要保持各级PFC设计的一致性。也可以采用均流措施［13，14］。一种两级交错有源PFC开环控制设计方案，如图4所示。

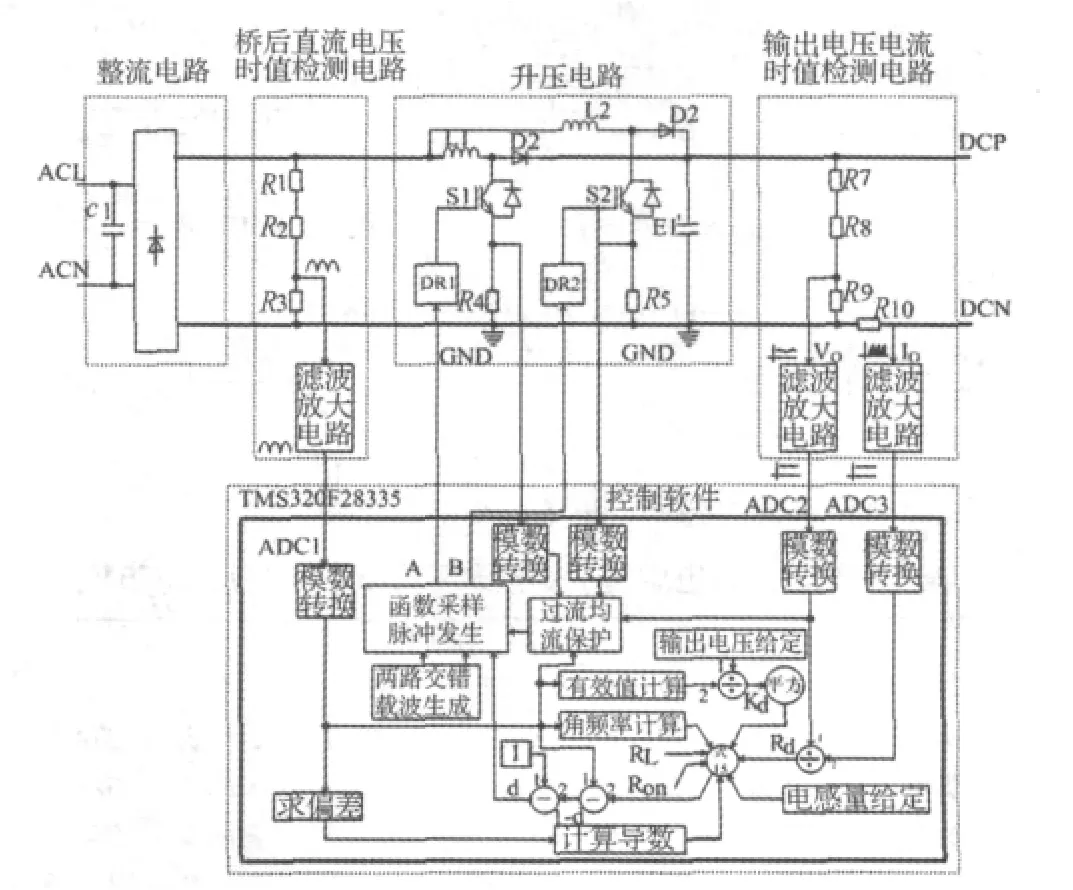
图4 两级交错有源PFC开环控制设计方案

2 有源PFC的开环控制实现仿真分析

利用MATLAB/Simulink建立图1所示的前馈开环控制功率电路。根据式（15），设计两套控制电路仿真图，如图5和图6所示。仿真参数如下:单相工频220 V交流输入，开关频率为35 kHz，输出功率可调，带电阻负载。

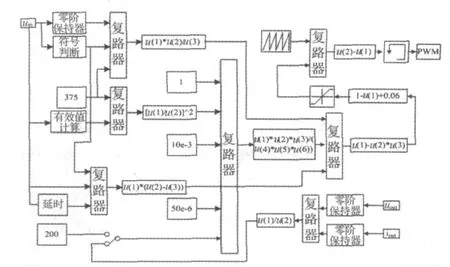
图5 开环控制仿真电路之一

仿真完全实现了单级、两级交错APFC的电路功能，具有良好的功率因数校正效果。期望输出电压为375 V时，输出电压与负载电阻、输入电压之间的关系如表1所示，此时k随着输入电压变化而变化。

如果保持额定输入电压（例如220 V），k=1.7，其它输入电压时默认为220 V，就会实现输出电压相对输入电压的电压跟随特性，如表2所示。

如果当输出功率改变时，适当反向地改变k，就会实现输出电压相对输出功率的电压跟随特性。电压跟随特性，有利于简化升压电感的设计。

图6 开环控制仿真电路之二

表1 不同负载电阻、输入电压下输出电压（期望375V）

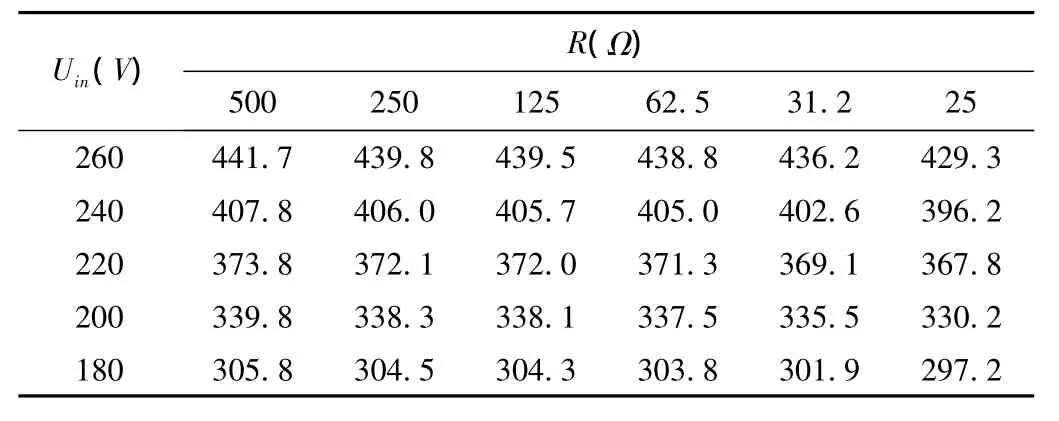
表2 不同负载电阻、输入电压下输出电压（k=1.7）

3 实验验证

为了验证上述分析的正确性，采用DSP TMS320F28335设计控制电路和应用程序，程序流程图可参见图3、4中的控制软件部分，搭建PFC实验平台进行实验。实验参数如下:输入电压Uin为220 V有效值，交流50 Hz频率。输出电压理论值为375 V，输出额定功率为3.0 kW。开关频率为35 kHz。电感感值为250 μH，最大流过电流为20 A。输出滤波电容选取6个680（F并联。IGBT型号为RJH60F7ADPK，100（C时可承受电流、电压分别为50 A、600 V。SiC反向快速恢复二极管型号为CSD20060D。经过测试，轻载下PFC部分效率不低于0.95，额定负载下PFC部分效率可达0.99以上。

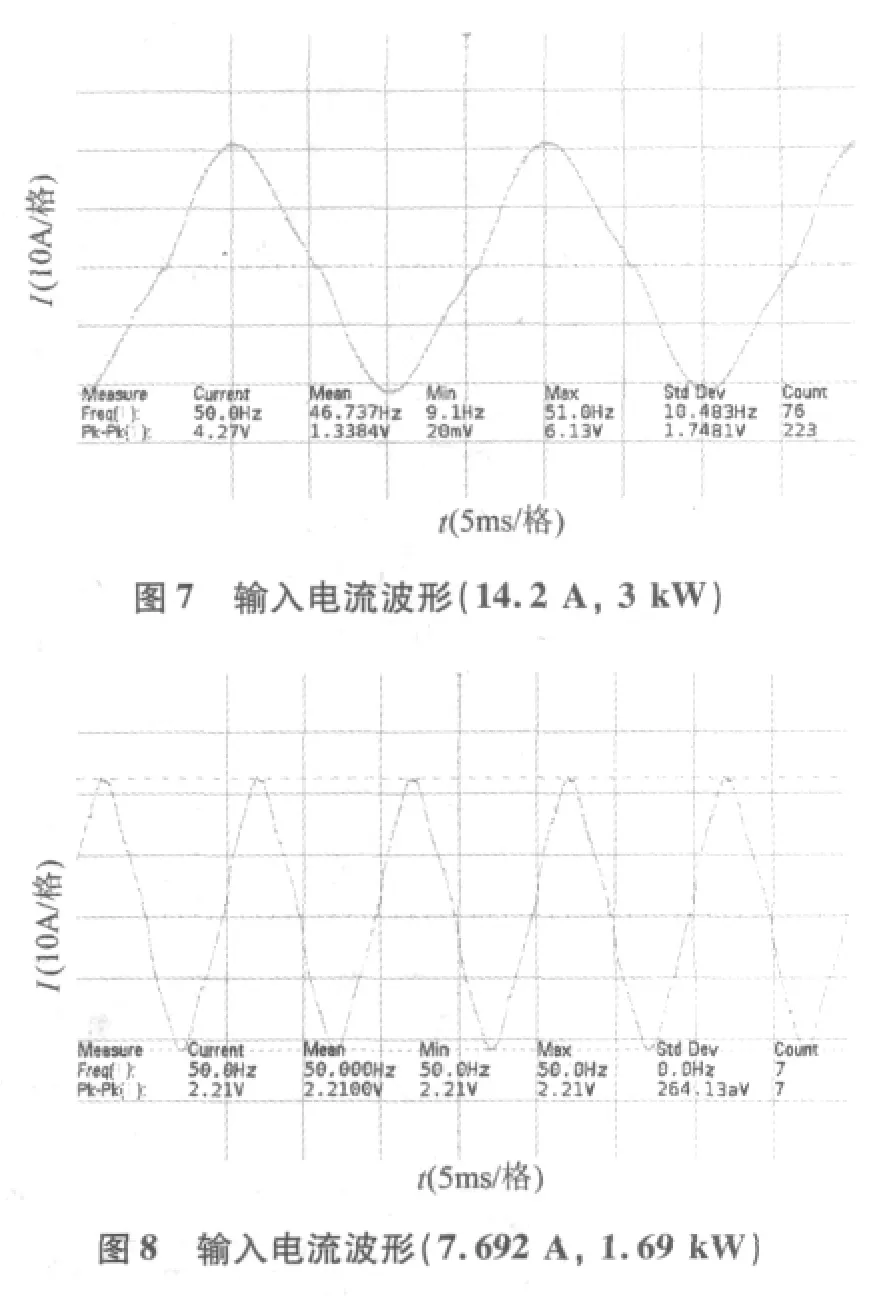
最终实现了单级和两级交错PFC的功率模块。图7和图8给出了在不同输入电压和输出功率时输入电流的实测波形，功率因数较高，实测输出电压平均值与仿真结果一致。

4 结束语

较深入地分析了一种只需检测整流桥后正弦半波电压和负载阻抗的开环控制策略，阐明了APFC占空比的组成和作用，可以认为是一种开环控制下的开关函数，并通过了仿真和实验验证。结果表明，采用该开环控制策略，一定输入电压条件下，输出电压平均值与输出功率无关。保持输出电压与输入电压有效值比值k不变，可以实现输出电压相对输入电压的跟随特性。根据负载功率大小，适当反向调节k，可以实现输出电压相对输出功率的跟随特性。在已知输入电压极性的条件下，无需检测输入电压有效值就可以实现控制。根据输出电压检测值，适当调节k大小，可以获得稳定或可调的输出电压。

［1］ ElectromagneticCompatibility. LimitsforHarmonicCurrentEmission（Equipment Input Current@16 A Per Phase）［S］，IEC 1000－3－2，1995.

［2］ Electromagnetic Compatibility.Overview of Immunity Tests Basic EMC Publication［S］，IEC 1000－4 －1，1992.

［3］ Electromagnetic Compatibility.General Guide on Harmonics and Interharmonics Measurements and Instrumentation for Power Supply Systems and Equipment Connected Thereto［S］，IEC 1000 －4 －7，1991.

［4］林海雪，孙树勤.电力网中的谐波［M］.北京:中国电力出版社，1998.

［5］田书欣.新型控制策略的数字有源PFC的实现［J］.电力电子技术.2010（2）:115－120.

［6］ Tokuo OHNISHI，Masahide HOJO.DC Voltage Sensor－less Single－Phase PFCConverter［J］.IEEETRANSACTIONS ON POWER ELECTRONICS，2004，19（2）:404 －410.

［7］刘霞.直流电压传感器的单相APFC变换器［J］.通信电源技术.2007（3）:28－30.

［8］李杭军，谢勇.DSP实现无输出电压采样的功率因数校正［J］.扬州大学学报（自然科学版）.2008（2）:45－49.

［9］ Wan feng ZHANG，Guang FENG，Yan Fei LIU.A Digital Power Factor Correction（PFC）Control Strategy Optimized for DSP［J］.IEEE Transactions ON Power Electronics，2004，19（6）:1474－1485.