不同边界和地基条件的大型滑坡体动力响应分析

卓 莉，何江达, ，谢红强, ，肖明砾,

（1. 四川大学 水利水电学院，成都 610065；2. 四川大学 水力学与山区河流开发保护国家重点实验室，成都 610065）

1 引 言

我国是世界上滑坡分布最广、危害最严重的国家之一。滑坡灾害不仅会造成人员伤亡，而且会造成巨大的经济损失，如 1985年三峡新滩滑坡[1]、2001年重庆武隆滑坡[2]、1989年云南漫湾水电站滑坡[3]。根据5.12地震后水电总院对岷江上游、涪江中上游以及白龙江下游的 22座水电工程的调查分析表明，地震触发的大量坍塌滑坡地质灾害对水工建筑物和设备造成了较严重的破坏，滑坡造成的损失约占整个地震损失的1/3[4－5]。随着我国的水电能源的深度开发，相当多的大型水电设施将建在我国多山、多地震的西部地区，滑坡堆积体的数量和面积巨大，大型滑坡体和深厚覆盖层的抗震问题成为边坡稳定的关键问题。

我国的地震动力响应研究在过去的几十年中也取得了许多有价值的成果。振动台试验是研究结构动力响应的方法之一，但振动台试验的“模型箱效应”会给试验结果带来一定的误差。近年来，计算机和有限元法的应用与发展为数值分析提供了强有力的工具，使其成为动力分析的重要手段，同时出现了很多边界模拟方法，如透射边界、黏弹性边界、无限边界元法等，这些模拟方法都大大提高了对边界条件的模拟精度，使正确评价结构动力响应成为可能。除了对边界的模拟，地震输入面的正确选择也是分析评价边坡动力响应的重要前提，但目前在不少的抗震设计中常误将场区设计峰值加速度直接与实际工程场地地表联系，任意假定作为自由场地表基准面的高程[6]，而且在学术界地震输入面的选择并没有达成共识，也没有统一的标准去遵循，从而导致计算地震响应值与真实值之间存在很大的差异。对边界的正确模拟和地震输入面的正确选择是评价滑坡体动力响应的前提。

滑坡研究源于20世纪20年代的瑞典，我国对滑坡的系统研究是建国后才开始的[1]，对滑坡体的研究主要集中于其形成机制研究及灾害评价，而对其地震响应研究并不多见。由于大型滑坡体体积大、下滑力大，而且存在潜在的滑动带，形成演化机制较复杂，与一般的边坡动力响应可能存在一定的差别，并且滑坡体动力响应分析是抗震防治措施的理论依据，因此，对大型或巨型滑坡体的地震响应研究具有非常重要的意义。本文以雅砻江卡拉水电站上田镇大型滑坡体为例，采用不同的边界条件和地基条件进行大型滑坡体的地震响应计算，揭示大型滑坡体的地震响应规律及地基辐射阻尼和地震输入高程对滑坡体动力响应的影响。

2 基于动力有限元的动力响应分析原理

在地震作用下，边坡的动力平衡方程用式（1）来描述：

式中：[M]、[C]、[K]分别为有限元模型的质量矩阵、阻尼矩阵和刚度矩阵；p(t)为与时间有关的动力荷载，已知输入地震加速度时程曲线为动力荷载可表示为｛u˙(t)｝、｛u( t)｝ 分别为相对加速度向量、速度向量、位移向量。阻尼矩阵采用Rayleigh阻尼，将阻尼矩阵简化为质量矩阵和刚度矩阵的线性组合，由式（2）计算：

式中：a和b分别为阻尼矩阵的刚度和质量比例因子，刚度项为与各相邻质体相对运动速度有关的阻尼力，质量项表示各质体与未受扰振地层相对运动速度有关的阻尼力，总的阻尼力则为两者的迭加。比例因子a和b可由式（3）、（4）计算：

式中：ζi与ωi分别为第i振型的阻尼比与自振频率。在计算边坡动力响应时一般认为，各阶振型的阻尼比相同，本次动力有限元分析中，根据《水工建筑物抗震设计规范》[7]取边坡介质材料的阻尼比为0.05。为了得到地震作用下边坡有限元模型微分方程的阻尼矩阵，对边坡进行模态分析，本文取前两阶振型对比例因子进行计算。

3 计算模型及计算参数

3.1 工程概况及计算参数

卡拉水电站工程区位于青藏高原向四川盆地过渡地带，是雅砻江中游河段规划开发的“一库六级”中的第6级，电站装机容量为980 MW，选坝河段自下而上仍分布着岗尖、田三、下田镇和上田镇 4个大型～巨型规模不等的滑坡体。上田镇滑坡体位于上坝址下坝线上游右岸约370～910 m处，表层崩坡积层主要为碎石土，厚2～25 m，灰黄色，稍实，见植物根，碎块石呈棱角、次棱角状，成分为砂质板岩、变质砂岩、大理岩；滑坡堆积土层主要成分为砂质板岩、大理岩，含量为70%～80%，粉质黏土含量为20%～30%，呈硬塑状；滑带土主要为碎石土，泥钙质胶结，胶结紧密，碎块石含量为70%～80%，粉质黏土含量为 20%～30%，基覆界面处典型滑带厚0.3～0.6 m，滑动面走向为N20°～30°W，倾向 NE，倾角 45°；下伏基岩为三叠系上统杂谷脑组（）地层，为砂质板岩（含泥质）、变质砂岩、大理岩、含炭质板岩互层，上田镇坡体全貌见图1，简化的边坡地质剖面图如图2所示。各岩体物理力学参数见表1。

图1 上田镇坡体全貌Fig.1 Panorama of Shangtian-town slip mass

图2 边坡地质剖面图Fig.2 Geological section of slope

表1 岩体物理力学参数Table 1 Physico-mechanical parameters of rock mass

3.2 滑坡动力计算模型

根据简化的地质剖面图建立二维有限元模型，采用平面应变单元模拟岩土体材料，边坡在地震作用下主要受自重和地震动荷载作用，在地下水位线以下的材料采用饱和重度，有限元模型如图3所示。为研究不同边界与地基模型条件下的上田镇滑坡体动力响应，本文共建立了4个模型进行计算分析，模型1、模型2、模型3都采用黏弹性边界，但模型1的地基为全质量地基；模型2河床底部以下岩体下半部分采用无质量模型；模型3河床底部以下岩体均无质量；模型4采用固定边界和全质量地基。在滑坡体中选取如图 4所示的特征点进行动力对比分析，特征点 1～4自上而下位于滑坡体主滑面的滑带土中，特征点2、5、6都位于高程2 020 m，水平深度分别为76.22、43.95、7.94 m，特征点3、7、6位于相同的水平位置，高程分别为1 971.09、1 995.55、2 020 m。

3.3 输入地震加速度

文献[8]通过沿滑面的应力积分法和动力时程分析法，发现竖向地震动可以显著地降低边坡动力安全系数，在输入地震动相同的条件下，其作用效应只略小于水平向地震动，对边坡的地震反应分析时考虑水平与竖向地震的共同作用更为合理。卡拉水电站工程场地地震基本烈度为Ⅶ度，上田镇滑坡体距坝址非常近，为A类Ⅱ级枢纽工程区边坡，边坡抗震设防类别为丙类，地震水平相对加速度代表值按基准期50年内超越概率10%为1.14 m/s2，竖向设计地震加速度取水平向设计地震加速度的2/3，计算时间步长为0.01 s，共计算15 s。基岩场地设计地震动加速度时程见图5。

图3 有限元计算模型Fig.3 The finite element calculation model

图4 特征点示意图Fig.4 Schematic of feature points

图5 输入地震波加速度时程曲线Fig.5 Time-history curves of acceleration of input seismic wave

4 不同边界条件下大型滑坡体动力响应

动力有限元法可计算得出边坡在地震作用下的动位移、加速度以及剪应力等的响应过程。由于地震纵、横波时差耦合作用的空间非均质性，即地震波强度沿特定斜坡体水平向及竖向均存在的放大特性[9－10]，为了便于分析，引入加速度放大系数，用符号n表示。坡体内任意一点的动力反应的加速度峰值为aimax，模型底部任意一点动力反应的加速度峰值为admax，则该点的加速度放大系数n就可以表示为 n =aimax/admax。

图6～10分别给出了模型1（黏弹性边界）和模型 4（固定边界）特征点动力响应时程曲线。从图中可知，在两种边界条件下滑带土中的剪应力都是随着高程的降低而增大，水平位移和竖向位移值却随着高程的降低而减小，从加速度放大系数来看，滑坡体质点的地震加速度响应值随水平深度的增大而减小，随高程的升高而增大；对比两种不同边界条件可知，在固定边界作用下，滑带土特征点1～4的最大剪应力值分别为240.380、84.159、66.676、35.120 kPa，而在黏弹性边界条件下的最大剪应力值分别为210.900、72.236、54.367、25.889 kPa，滑带土特征点在固定边界条件下的最大剪应力值明显大于黏弹性边界条件下的最大剪应力值，差值在10%～40%之间。

图6 滑带土特征点剪应力-时程曲线Fig.6 Shear stress-history curves of characteristic points in slip soil

图7、8给出了模型1和模型4的滑坡体加速度放大系数与水平深度及高程的关系曲线，在黏弹性边界条件下滑坡体加速度的放大系数在1～3之间，而在固定边界条件下加速度放大系数处于 2～4范围内。从图9、10中的位移时程曲线可知，模型1滑带土特征点的水平位移的最大值为30 mm，竖向位移最大值为20 mm，而模型4的滑带土特征点水平位移最大值达到了 120 mm，竖向位移最大值为30 mm，在固定边界条件下的滑带土的位移响应值较黏弹性边界条件下的位移响应值大。

图7 滑坡体加速度放大系数-水平深度的关系曲线Fig.7 The relation curves between amplificatory coefficient of acceleration and level depth

图8 滑坡体加速度放大系数-高程的关系曲线Fig.8 The relation curves between amplificatory coefficient of acceleration and elevation

图9 滑带土特征点水平位移-时程曲线Fig.9 Horizontal displacement-history curves of characteristic points in slip soil

图10 滑带土特征点竖向位移-时程曲线Fig.10 Vertical displacement-history curves of characteristic points in slip soil

从图6～10中的曲线数据，无论是剪应力，还是加速度放大系数、位移响应值，都可以得出，固定边界的地震响应值大于黏弹性边界的地震反应。这主要是由于固定边界会反射地震波，入射波和反射波的共同作用造成滑坡体的振动加大，扩大了滑坡体的地震响应。而实际情况中滑坡体处于一个半无限体中，地震作用时振动能量通过无限介质向外传递，这就是无限地基的辐射阻尼作用。黏弹性边界等效为弹簧与阻尼器并联的系统，由于其时空解耦性在地震分析中获得了广泛的应用，此边界不仅可以反映波动能量在原连续介质中的辐射现象，而且能保证波动从截断区内部穿过人工边界时不会产生反射效应，能较真实地反映地震过程中滑坡体的动力响应。

5 不同地基条件下大型滑坡体动力响应

通过对黏弹性边界条件下不同地基模型的计算，得出图11～14的计算结果。图11给出了模型1、2、3滑带土特征点的剪应力-时程曲线，从图中曲线数据可知，采用全质量地基时，特征点1和4的最大剪应力分别为15.889、210.900 kPa，当河床以下岩体下半部分无质量（模型 2）时，特征点 1和4的最大剪应力值分别降低了8.6%和6.68%；而当河床以下岩体都采用无质量条件时，特征点1和4的最大剪应力值与模型一相比降低了 21.13%和20.12%。从图 12、13中加速度放大系数与滑坡体中点的位置曲线关系可知，模型1的滑坡体加速度放大系数最大，模型2加速度放大系数次之，模型3滑坡体的加速度放大系数最小。从图14中的位移-时程曲线看，模型1特征点的水平位移和竖向位移值均大于模型3中相同特征点的位移响应值。

从以上的数据分析可看出，无质量地基模型的地震响应值小于全质量地基模型的响应值，无质量地基的范围越大，滑坡体的动力响应值越小，无质量地基模型忽略地基质量而只考虑其刚度对结构动力反应的影响，消除了地基对地震运动的放大作用，可认为地震波是从无质量地基高程顶部输入。从全质量地基和无质量地基模型的计算成果来看，地基对地震波动的放大效应是不容忽视的，地基的这种放大效应使坡体上的地震输入与实际地震输入相差较大，这就使得滑坡体的动力响应会偏离真实反映值，地震输入高程的不同将使滑坡地震响应在量值上产生很大影响。

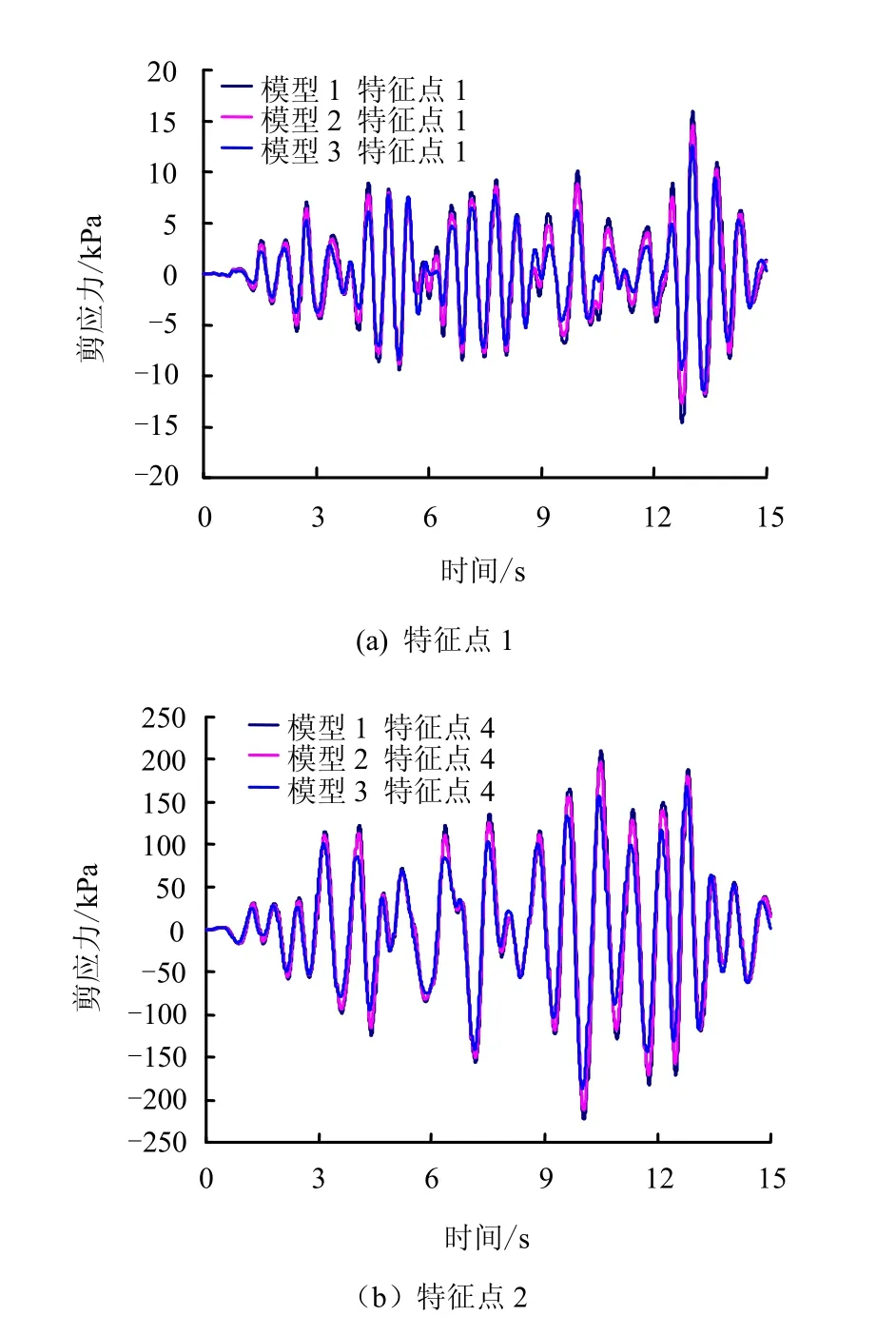
图11 滑带土特征点剪应力-时程曲线Fig.11 Shear stress-history curves of characteristic points in slip soil

图12 滑坡体加速度放大系数-水平深度的关系曲线Fig.12 The relation curves between amplificatory coefficient of acceleration and level depth

图13 滑坡体加速度放大系数-高程的关系曲线Fig.13 The relation curves between amplificatory coefficient of acceleration and elevation

图14 黏弹性边界滑带土特征点位移-时程曲线Fig.14 Displacement-history curves of characteristic points in slip soil under viscoelastic boundary

6 大型滑坡体动力响应分析

从不同模型的滑带土位移-时程曲线可知，在地震作用下，滑带土中位移响应值随高程降低有所减小，这可能与上田镇滑坡体的自身特性有关，滑坡体上部厚度较薄，主要为后期的崩坡积物碎石土，而且坡度较陡，则不利于上部滑坡体的稳定性，在地震的振动作用下，很容易出现较大的地震响应。上田镇滑坡体中下部坡体较厚而且地形相对平缓，自稳性较好，所以地震响应比上部坡体小。

滑带土中的剪应力却是随高程降低而增大，与滑带土中的位移响应正好出现相反的规律，滑坡体上部位移大而剪应力相对较小使得滑带土上部可能会出现拉裂破坏，相反位移响应值小但剪应力大的下部可能会出现剪切破坏，由此可推出，在地震作用下上田镇大型滑坡体的可能失稳模式：上部滑带出现一定深度内的拉裂破坏，下部滑带土形成向上延伸的剪切滑移带，最终形成贯通的滑移面导致滑坡体的失稳，这与汶川地震边坡调研[11]发现大量边坡破坏形式为坡顶拉裂、下部坡体剪切破坏的规律是一致的。

由弹性波散射理论可知[12]，入射的地震波传播到坡面时将产生波场分裂现象，分解为同类型的反射波和不同类型转换波，各种类型的波相互叠加形成复杂的地震波场，使加速度响应在坡面和坡顶显著增大，所以滑坡体加速度放大系数与水平深度成反比，与高程成正比。

7 结 论

（1）相对固定边界模型的滑坡体地震响应来讲，考虑无限地基辐射阻尼作用的黏弹性边界于对滑坡体地震响应的削减作用是显著的，在地震分析中地基辐射阻尼对滑坡体动力响应作用不可忽视。无质量地基可减小地基对地震波的放大作用，说明地震波输入高程的变化对滑坡体的动力响应有较大的影响。

（2）上田镇大型滑坡体在地震作用下后缘的位移值大于前缘，而剪应力值却小于前缘，此滑坡体在地震作用下可能出现上部的拉裂破坏和下部的剪切破坏，滑坡体质点的动力响应与水平深度成反比，与高程成正比。

（3）对边坡滑坡体地震响应的正确模拟是边坡抗震设计的重要依据。利用动力有限元对滑坡体地震响应模拟的正确性很大程度上取决于对地基辐射阻尼的正确模拟和地震波的正确输入。

[1]吴圣林. 崩塌一推覆滑移地质体成因机理及其稳定性研究[D]. 徐州：中国矿业大学, 2008.

[2]文海家, 张永兴. 山区建设场地高切坡稳定性评估概要[J]. 地下空间, 2002, 22(4): 299－302.WEN Hai-jia, ZHANG Yong-xing. Summary on stability assessment for man-excavated high slope adjacent to building site in mountain areas[J]. Underground Space,2002, 22(4): 299－302.

[3]孟晖, 胡海涛. 我国主要人类工程活动引起的滑坡、崩塌和泥石流灾害[J]. 工程地质学报, 1996, 4(4): 70－74.MENG Hui, HU Hai-tao. Disaster of lanslides, rockfalls,and mudflows induced by human engineering in China[J].Journal of Engineering Geology, 1996, 4(4): 70－74.

[4]晏志勇, 王斌, 周建平, 等. 汶川地震灾区大中型水电工程震损调查与分析[M]. 北京: 中国水利水电出版社, 2009.

[5]郑颖人, 叶海林, 黄润秋. 地震边坡破坏机制及其破裂面的分析探讨[J]. 岩石力学与工程学报, 2009, 28(8):1714－1723.ZHENG Ying-ren, YE Hai-lin, HUANG Run-qiu.Analysis and discussion of failure mechanism and fracture surface of slope under earthquake[J]. Chinese Journal of Rock Mechanics and Engineering, 2009,28(8): 1714－1723.

[6]陈厚群. 坝址地震动输入机制探讨[J]. 水利学报, 2006,37(12): 1417－1423.CHEN Hou-qun. Discussion on seismic input mechanism at dam site[J]. Journal of Hydraulic Engineering, 2006,37(12): 1417－1423.

[7]中国水利水电科学研究院. DL5073－2000 水工建筑物抗震设计规范[S]. 北京: 中国电力出版社, 2000.

[8]黄诚, 王安明, 任伟中. 水平向与竖向地震动的时间遇合模式对边坡动力安全系数的影响[J]. 岩土力学, 2010,31(11): 3404－3410.HUANG Cheng, WANG An-ming, REN Wei-zhong.Influence of time combination pattern of horizontal and vertical ground motions on slope seismic safety factor[J].Rock and Soil Mechanics, 2010, 31(11): 3404－3410.

[9]秋仁东, 石玉成, 付长华. 高边坡在水平动荷载作用下的动力响应规律研究[J]. 世界地震工程, 2007, 23(2):131－138.QIU Ren-dong, SHI Yu-cheng, FU Chang-hua. General laws of dynamic responses of the high slopes under horizontal dynamic input[J]. World Earthquake Engineering, 2007, 23(2): 131－138.

[10]王环玲, 徐卫亚. 高烈度区水电工程岩石高边坡三维地震动力响应分析[J]. 岩石力学与工程学报, 2005,24(2): 5890－5895.WANG Huan-ling, XU Wei-ya. 3D dynamical response analysis of high rock slope related to hydropower project in high intensive seismic region[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(2): 5890－5895.

[11]言志信, 张森, 张学东, 等. 地震边坡失稳机理及稳定性分析[J]. 工程地质学报, 2010, 18(8): 844－850.YAN Zhi-xin, ZHANG Sen, ZHANG Xue-dong, et al.Failure mechanism and stability analysis of slope under earthquake[J]. Journal of Engineering Geology, 2010,18(8): 844－850.

[12]徐光兴, 姚令侃, 高召宁, 等. 边坡动力特性与动力响应的大型振动台模型试验研究[J]. 岩石力学与工程学报, 2008, 27(3): 624－622.XU Guang-xing, YAO Ling-kan, GAO Zhao-ning, et al.Large-scale haking table model test study of dynamic characteristics and dynamic responses of slope[J].Chinese Journal of Rock Mechanics and Engineering,2008, 27(3): 624－622.