结构性吹填软土蠕变模型研究

杨爱武 ，闫澍旺，杜东菊

（1. 天津城市建设学院 土木工程系，天津 300381；2. 天津城市建设学院 天津市软土工程特性与工程环境重点实验室，天津 3003811；3. 天津大学 建筑工程学院，天津 300381）

1 引 言

天津滨海新区属于典型的淤泥质海岸，蜿蜒的海岸、巨厚的淤泥质河口沉积，决定了进行人工造陆时其吹填物质主要以细粒土为主，黏土矿物所占比例高达50%以上，并以伊利石、伊蒙混层为主，这是在我国东部沿海地区吹填造陆中比较特殊的吹填物源，这种物质组成使其有别于我国其他地区吹填土，经过真空预压地基处理后，其结构性强，蠕变变形不可低估。由于结构性和蠕变特性的存在，使得吹填场地工后沉降计算及控制显得更为复杂。现有的各种本构模型实际上都是针对饱和扰动土和砂土而发展起来的，考虑结构影响的较少，且主要是弹性非线性以及弹塑性模型[1－5]，对于蠕变模型的研究则相对较少[6－10]。现实的土体都具有结构性[11－12]，这一内在因素对土体力学性能，当然也包括土体的本构关系具有重要的影响，其结果必然是计算数值与实际情况有一定的差距。本文在前人研究的基础上，以半理论半经验蠕变模型为基础，将结构性影响引入到模型中，尝试建立考虑结构性的黏弹塑性本构模型，对于减少和防治吹填场地工后沉降具有巨大的经济效益。

2 三轴蠕变试验

2.1 土的基本性质

本文研究的样品取自天津滨海新区临港工业区经过真空预压处理的吹填场地，其物理力学性质如表1所示。无侧限抗压强度曲线见图1，一维压缩曲线见图2。

表1 吹填软土的物理力学表Table 1 Basic physico-mechanical parameters of soft dredger fill

图1 无侧限抗压强度Fig.1 Unconfined compressive strength

图2 一维压缩曲线Fig.2 One-dimensional compression curves

从表1可以看出，经过真空预压处理后的吹填软土亦为高含水率软土。由图1可知，原状样与重塑样（按与原状样相同的含水率及重量进行制样）无侧限抗压强度曲线都表现为应变硬化型。原状样无侧限抗压强度要比相同应变下重塑土的无侧限抗压强度高，其差值为结构性作用的结果。再由图 2可知，重塑土压缩曲线为直线，原状土压缩曲线不为直线，可用两条折线拟合，两直线的交点即为结构屈服应力。总之，吹填软土经过真空预压处理后具有明显的结构性，在实际工程应用中要考虑到其结构性的影响。

2.2 蠕变试验

对于有结构性的吹填软土，原状土与重塑土性质差别很大，蠕变也不例外。目前天津滨海新区吹填场地最大深度在10 m左右，为了使研究的成果更符合现场工程实际，所采用的最大围压为100 kPa。由于吹填软土为高塑性指数的黏土，且现场实际中不会有好的排水条件，因此，本文仅开展了不同围压下的不固结不排水蠕变试验，试验样品为原状样及其相应的重塑样。试验仪器采用TSS10土体三轴蠕变试验仪，不同偏应力S作用下变形随时间变化如图3所示。

图3 不同围压下的不固结不排水蠕变变形历时曲线Fig.3 Creep diachronic curves of unconsolidated undrained test under different confining pressures

图3表明，结构性的存在，原状土与重塑土的蠕变有明显区别。首先是应力水平相同时，原状土的蠕变量小于重塑土，再次是最终的蠕变破坏应力水平也是原状土大于重塑土。

3 考虑结构性蠕变模型的建立

由文献[13]对吹填软土应力-应变等时曲线分析知：在任意一级荷载下任意一时刻的应变都可分解成线性黏弹性应变、线性黏塑性应变以及非线性黏塑性应变。因此，本文采用这种方法来建立滨海吹填软土的非线性蠕变本构模型。即将吹填软土的总变形分为线性蠕变部分和非线性蠕变部分，线性蠕变部分用模型理论来研究，而非线性蠕变部分则用一经验模型来描述。当应力小于原状土结构屈服应力或重塑土屈服应力时，吹填软土表现为线性黏弹性特征；当应力大于原状土结构屈服应力或重塑土屈服应力时，则表现为非线性黏塑性特性，其中黏塑性变形又可分为线性黏塑性变形和非线性黏塑性变形的叠加。因此，吹填软土的蠕变模型可以用线性黏弹性模型（包括瞬时弹性变形）、线性黏塑性模型与非线性黏塑性模型三者串联而成，具体模型如图4所示。

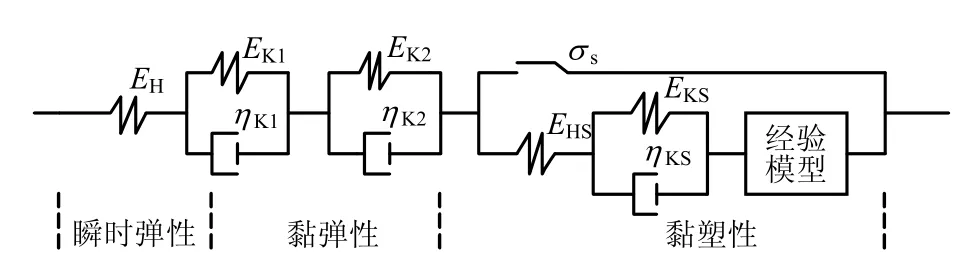
图4 吹填软土蠕变模型Fig.4 Creep model of soft dredger fill

图4中：EH为虎克体弹簧模量；EKi、ηKi为Kelvin体弹性模量和黏滞系数；EHS为虎克体弹簧模量；EKS、ηKS为Kelvin体弹性模量和黏滞系数；σs为开关即屈服函数。屈服函数的选用是模型建立的关键。屈服函数决定了土体何时进入屈服状态即蠕变状态，对蠕变变形量大小的计算起着重要的作用。传统的屈服函数如Drackev-Prager（简称D-P）模型、修正的剑桥模型等都未考虑结构性的影响，作为屈服状态的开关时，忽略结构性的存在，使计算结果与实际有出入。本文将以修正的剑桥模型为基础，对其进行改进，使其考虑结构性的影响，再以此作为屈服函数，结合蠕变特性试验成果，建立一个适合吹填场地实际的蠕变本构模型。

3.1 对土的强度包线的处理

剑桥模型假定正常固结土的强度包线在p′-q平面上是通过坐标原点的（见图 5）。实际上土具有凝聚力，邓肯建议采用强度包线不通过原点，而在p′轴上相交于离原点距离为pr′（见图6），也就是说所有公式中有关p′的量都应加上pr′的值。本文认为还不够，由于结构的存在，强度包线不应为直线，而应为折线，折线交点处为剪切屈服应力，具体见图7。

图5 修正剑桥模型示意图Fig.5 Sketch of modified Cambridge model

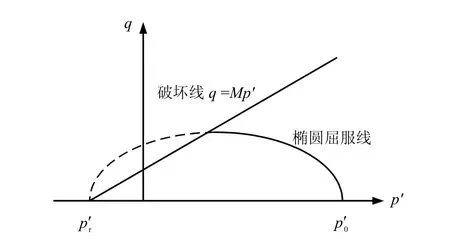
图6 邓肯对剑桥模型的修正Fig.6 Modified Cambridge model of Duncan

图7 本文对剑桥模型的修正Fig.7 Modified Cambridge model by the authors

3.2 对等向压缩曲线的处理

剑桥模型假定等向压缩曲线的斜率λ为常数（见图 8）。邓肯认为，等向压缩曲线的斜率λ不是常数，可随p′改变而改变。因此，输入λ的是一系列数值，在计算时通过内插来决定处于某一应力状态的λ值。本文对其进行简化，认为压缩斜率λ分为两段，分界点处为同向固结结构屈服应力，如图9所示。

根据等向固结试验得到以塑性体积应变为硬化参量的剑桥模型屈服函数为[14]

式中各符号含义详见文献[14]。

本文按以上对土的强度包线的处理以及对等向压缩曲线的处理对修正剑桥模型进行改进。在计算时，将式（1）中λ、M 在结构屈服应力前后分别用λ1、λ2以及M1、M2代替。

图8 剑桥模型等向压缩曲线Fig.8 Isotropic compression curves of Cambridge model

图9 本文改进的剑桥模型等向压缩曲线Fig.9 Improved isotropic compression curves of Cambridge model by the authors

4 蠕变模型参数的确定

4.1 线性黏弹性模型参数的确定

本文将线黏弹性部分采用可以描述衰减稳定蠕变的最简单模型Merchant模型与Kelvin体串联，Merchant体是由一个 Kelvin体和一个弹簧串联而成。线性黏弹性蠕变方程为

5个待定参数EH、E1、η1、E2、η2，采用Origin软件[15]，通过相应的函数对曲线进行拟合来确定。线性黏弹性参数见表2。

表2 线性黏弹性蠕变变形参数Tasble 2 Deformation parameters of linear viscoelastic creep

4.2 线性黏塑性模型参数的确定

线性黏塑性同样也用模型理论来研究，将应力-应变等时曲线上的线性黏弹性应变分离后，得到的黏塑性应力-应变等时曲线，其端点处切线即为线性黏塑性蠕变柔量Jlp(t)。

本文将线性黏塑性部分用一摩阻滑块与Merchant体并联的模型，摩阻滑块表示蠕变门槛值，大于此值时将产生塑性应变，否则，塑性应变为0。线性黏塑性蠕变方程为

模型中3个待定参数EHS、EKS、ηKS，采用与黏弹性同样的方法采用相应的函数进行拟合，拟合参数见表3。

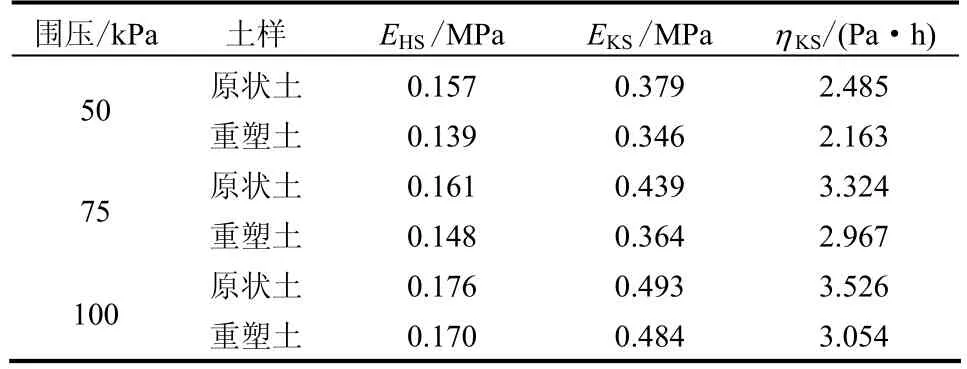
表3 线性黏塑性蠕变变形参数Table 3 Deformation parameters of linear viscoplastic creep

4.3 非线性黏塑性模型参数的确定

非线性黏塑性变形可用经验公式来描述，一般可以用幂函数来描述，即非线性应变εnp与应力的关系为

式中：εnp为未除去瞬时非线性变形以后的非线性变形，它与时间有关，不考虑t =0时的非线性变形；At为非线性变形系数；m为硬化系数。

对于模型中的3个待定参数At、m、β，可用Origin软件中设定的相关函数进行拟合，拟合后的结果如表4。

表4 非线性黏塑性蠕变变形参数Table 4 Deformation parameters of nonlinear viscoplastic creep

表4数据表明，原状土与重塑土参数基本上无太大差别，说明非线性塑性阶段土体的结构性基本上可以忽略，即其已基本上不起作用。

综上所述，图4中天津滨海新区吹填软土非线性蠕变本构模型可表示为3部分的叠加，即

式中：σs为重塑土为屈服应力，对结构性原状土为结构屈服应力。

式（7）即为天津滨海吹填软土的蠕变本构模型，它包括线性黏弹性变形εlve、线性黏塑性变形εlvp和非线性黏塑性变形εnvp。

5 一维到三维转换

在多维情况下，蠕变模型很难用形象化的物理元件表达。假定软黏土为各向同性材料，则蠕变本构方程可以利用一维模型采用类比的方法直接导出，称为“泛化”。

根据Perzyna[16]原理并参考文献[17]，将式（7）的一维非线性蠕变本构方程推广到三维情况，即

6 模型应用

应用本文建立的本构模型，计算了 3个围压（50、75、100 kPa）不同应力下的吹填软土蠕变发展趋势。将对应的时间和应变数据代入本构模型，拟合出应力-应变关系曲线，并与蠕变试验曲线数据进行对比，如图10、11所示。

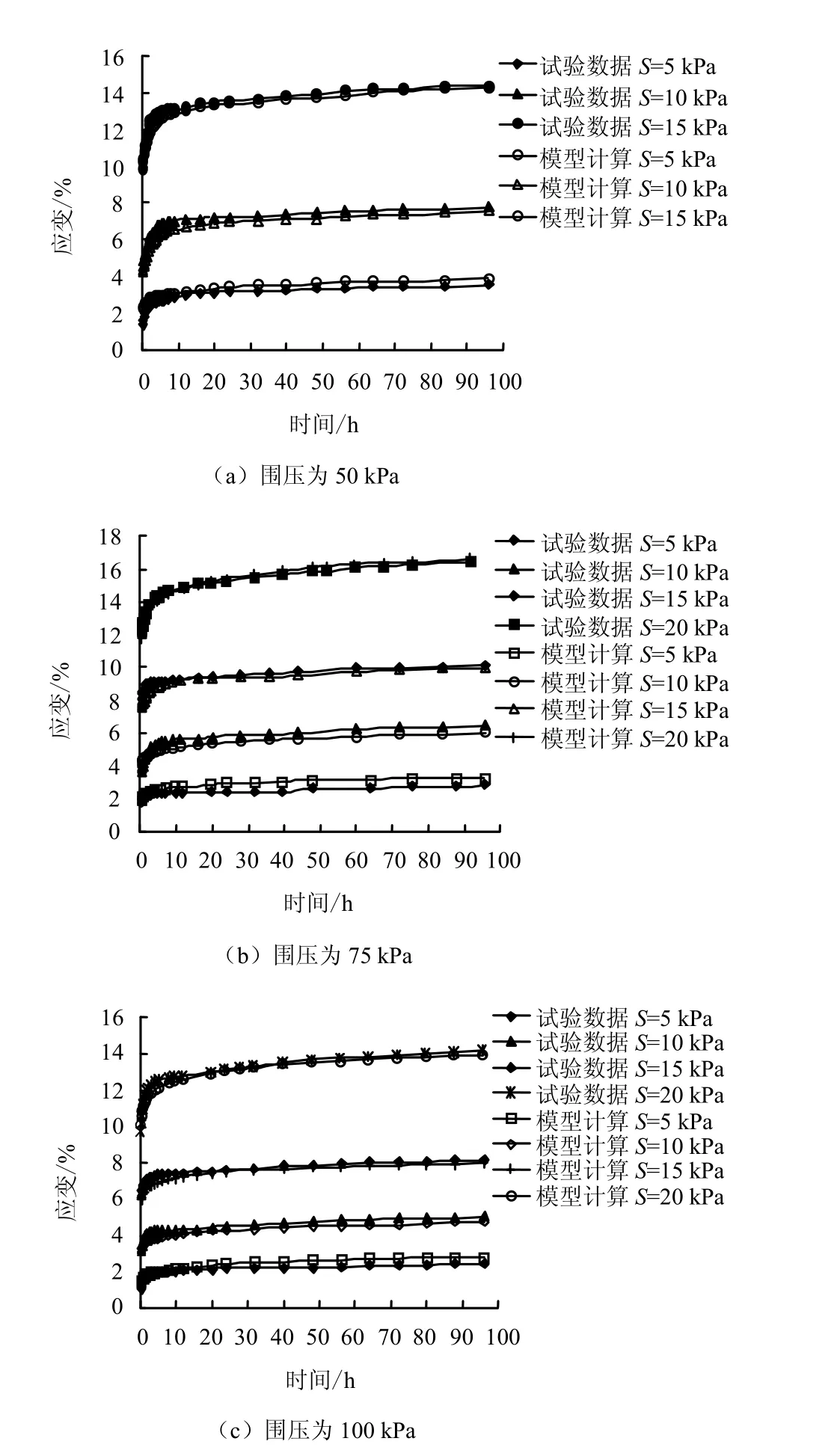
图10 原状土应力-应变实测值与计算值对比Fig.10 Measured and calculated stress-strain values of undisturbed soil

图11 重塑土应力-应变实测值与计算值对比Fig.11 Measured and calculated stress-strain values of remolded soil

图10、11表明，实测值与计算值吻合得较好，说明本文建立的模型可以反映吹填软土蠕变特性。但比较原状土与重塑土的拟合结果发现，重塑土更精确，原状土在初始阶段拟合效果略差，原因是一维模型中原状土只用结构屈服应力代替了屈服应力，结构性影响不能很好地反映出来，三维模型计算优势会明显。另外，原状土在蠕变过程中会有结构破损，表现为开始黏弹性阶段模型参数会逐渐劣化变小，而计算时用一固定值，因此，计算结果与实测值有偏差。因此，在建模时考虑到结构损伤的影响，会使模型更加完美地反映结构性土的蠕变特性。

7 结 论

（1）天津滨海新区吹填软土经过真空预压处理后形成了一定的结构性，结构性的存在使原状吹填软土蠕变特性明显区别于重塑土。

（2）通过对修正的剑桥模型进行改进，使其考虑结构性的影响，并以其作为蠕变屈服函数，建立了考虑结构性影响吹填软土蠕变模型。

（3）本文的模型未考虑结构性损伤的影响，深入开展此方面研究，建立更完善的蠕变模型显得十分必要。

[1]沈珠江. 结构性黏土的弹塑性损伤模型[J]. 岩土工程学报, 1993, 15(3): 21－28.SHEN Zhu-jiang. An elasto-plastic damage model for cemented clays[J]Chinese Jounal of Geotechnical Engineering, 1993, 15(3): 21－28.

[2]沈珠江. 结构性黏土的堆砌体模型[J]. 岩土力学, 2000,21(1): 1－4.SHEN Zhu-jiang. A masonry model for structured clays[J]. Rock and Soil Mechanics, 2000, 21(1): 1－4.

[3]饶为国, 赵成刚, 王哲, 等. 一个可考虑结构性影响的土体本构模型[J]. 固体力学学报, 2002, 23(11): 34－39.RAO Wei-guo, ZHAO Cheng-gang, WANG Zhe, et al. A constitutive model considering the influence of soil structure[J]. Acta Mechanica Solida Sinica, 2002,23(11): 34－39.

[4]王国欣, 肖树芳, 黄宏伟, 等. 基于扰动状态概念的结构性黏土本构模型研究[J]. 固体力学学报, 2004, 25(2):191－197.WAND Guo-xin, XIAO Shu-fang, HUANG Hong-wei,et al. Study of constitutive model of structural clay based on the disturbed state concept[J]. Acta Mechanica Solida Sinica, 2004, 25(2): 191－197.

[5]王立忠, 沈恺伦. K0固结结构性软黏土的本构模型[J].岩土工程学报, 2007, 29(4): 496－504.WANG Li-zhong, SHEN Kai-lun. A constitutive model of K0consolided structured soft clays[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(4): 496－504.

[6]廖红建, 俞茂宏. 黏性土的弹黏塑性本构方程及应用[J]. 岩土工程学报, 1998, 20(2): 41－44.LIAO Hong-jian, YU Mao-hong. Elasto visco-plastic constitutive equation of cohesive soils and its application[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(2): 41－44.

[7]SINGH A, MITCHELL J K. General stress-strain-time function for soils[J]. Journal of Soil Mechanics and Foundation Division, ASCE, 1968, 94(1): 21－46.

[8]YIN Jian-hua, ZHU Jun-gao. Elastic visco-plastic consolidation modeling of soft clay[J]. Chinese Journal of Geotechnical Engineering, 1999, 21(3): 360－365.殷建华, 朱俊高. 软土弹黏塑性固结模拟[J]. 岩土工程学报, 1999, 21(3): 360－365.

[9]MESRI G, EEHRES-CORDERO E, SHIELDS D R, et al.Shear stress-strain-time behaviour of clays[J].Geoechnique, 1981, 31(4): 537－552.

[10]殷德顺, 任俊娟, 和成亮, 等. 一种新的岩土蠕变模型元件[J]. 岩石力学与工程学报, 2007, 26(9): 1899－1903.YIN De-shun, REN Jun-juan, HE Cheng-liang, et al. A new creep model element for geo-materials[J]. Chinese Journal of Rock Mechanics and Engineering, 2007,26(9): 1899－1903.

[11]MESRI G. New design procedure for stability of soft clays[J]. Journal of the Geotechnical Engineering Division, ASCE, 1975, 101(4): 409－412.

[12]KABBAJ M, TAVENAS F, LEROUEILS. In situ and laboratory stress-stain relationships[J]. Geotechnique,1988, 38(1): 83－100.

[13]杨爱武. 结构性吹填软土蠕变特性及其本构模型研究[D]. 天津: 天津大学, 2011.

[14]罗汀, 姚仰平, 侯伟. 土的本构关系[M]. 北京: 人民交通工业出版社, 2010.

[15]方安平, 叶卫平. Origin 8.0 实用指南[M]. 北京: 机械工业出版社, 2010.

[16]PERZYNA P. fundamental problems in viscoplasticity[C]//Recent Advances in Aoolied Mechanics.New York: Acedemic Press, 1966.

[17]孙钧. 岩土材料蠕变力学及其工程应用[M]. 北京: 中国建筑工业出版社, 1999.