基于度量方法的阔叶红松林区树种树高曲线模型的研究

陈立莉

(东北林业大学)

0 引言

在林木各调查因子之间，均存在着紧密的相关关系，研究和探讨这些相关关系，是揭示林木结构和生长规律的基础.因此，林木生长很可能将会成为新世纪的热门科学之一.在实际的林业调查中，调查结果会受到诸如林分密度、树高、胸径等很多因素的影响，但树高和胸径是衡量林分生长标准的两个重要的指标，是最重要的因子.他们与树的年龄成正相关，同时二者之间也成正相关.胸径和树高的这种特殊的性质，决定了其在林业生产和科学研究中的重要的不可替代的作用.在树高曲线模型的研究中，向玮等［1］、孙圆等［2］、曾翀等［3］、王晓琳等［4］分别对湖南黄丰桥林场杉木、江苏省杨树、落叶松云冷杉林单木、柞树等树种的树高曲线都做了比较系统的研究，说明了在进行树种生长模拟实验时，不同的树种林分所适合的最优树高曲线是不同的，我们在研究室必须根据树种林分类型的不同选取不同的树高曲线模型.该文以黑龙江省带岭林业局东方红林场3个标准样地为研究对象，通过对以往研究中精度较高的非线性标准树高曲线通过回归分析，以确定阔叶红松林区各主要树种在不同林分中所适合的最优生长模型.

1 研究地概况

以东方红林场为研究区，面积为18 984 hm2，位于黑龙江省伊春地区带岭林业局境内.该地区地处中温带，属大陆性季风气候，全年平均气温为1.4℃，无霜期为115 d左右.植物属于长白山植物区系.原地带性的植被为阔叶红松林.研究数据来自于东方红林场3个标准样地的1997年调查的数据.

2 研究方法

2.1 数据来源

在带岭林业局东方红林场选取了阔叶红松林区具有代表性的三个林分类型:白桦林分、过伐林分和柞木林分作为样地，其中每个样地为25 m×40 m.在三个样地中，分别选取了树高大于1.3 m、株数大于10棵的树种为研究对象，具体数据取值范围见表1.

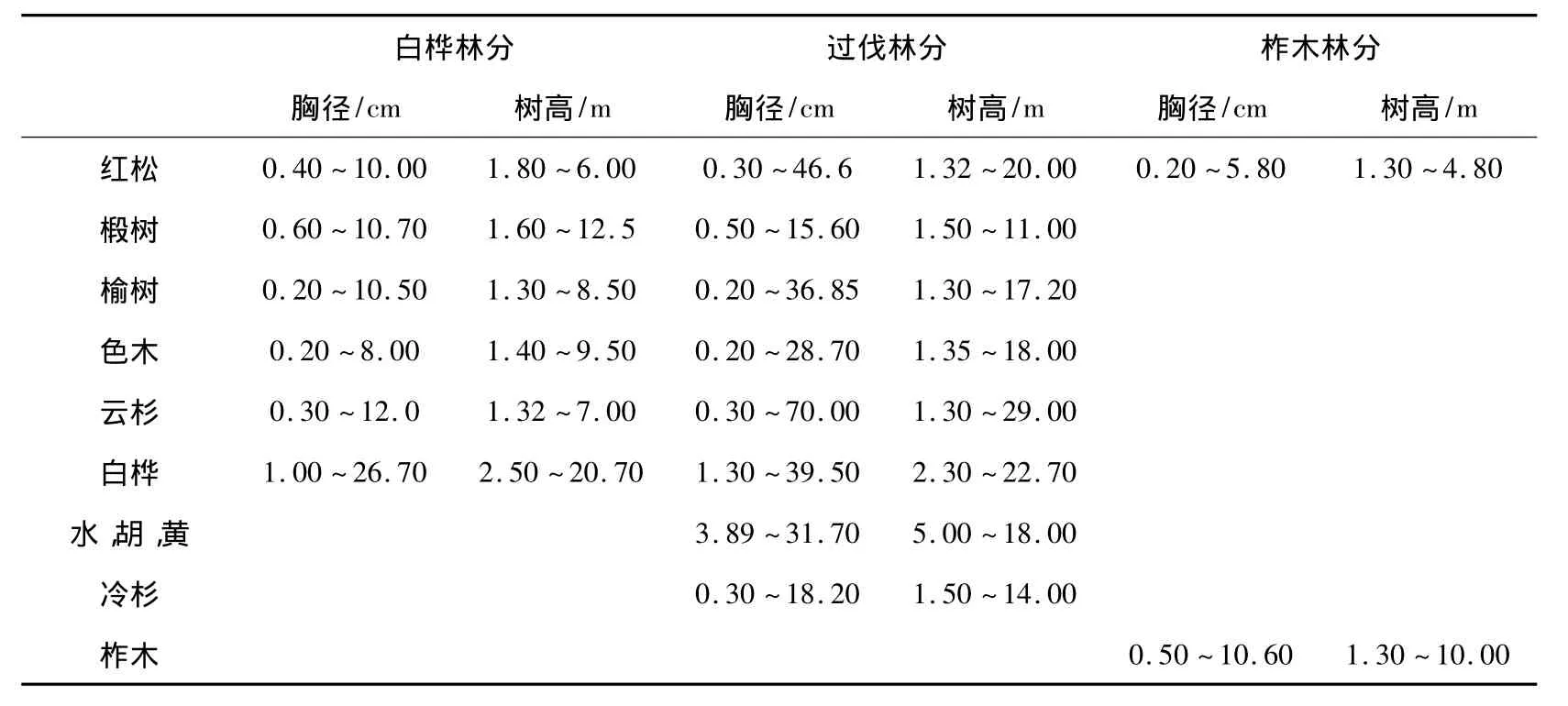
表1 三个样地树种数据范围

2.2 研究方法

该文针对阔叶红松林区的3种林分类型样地进行了森林调查，根据样地的调查数据，列出了一些比较常用的树高曲线模型(详见表2)，分别对以下10种标准树高曲线模型进行非线性度量误差分析，根据分析结果选择最优模型并进行比较，从而找出不同林分中各树种所适应的树木最优生长方程.

表2 树高曲线模型

表2中，H为树高，D为胸径，a、b、c为方程参数.

3 结果与分析

根据现有样地资料，利用统计之林(ForStat)2.1软件，分别对表2中10个模型进行度量误差模型分析.

3.1 白桦林分主要树种树高曲线模型的确定

利用统计之林(ForStat)2.1软件对白桦林分中主要树种红松、椴树、榆树、色木、云杉和白桦的树高与胸径的关系进行了度量误差模型分析，结果见表3.

从表3中由决定系数R2和残差平方和SSE可以看出:在白桦林分中，红松、椴树、榆树、色木和白桦都以抛物线型H=a+bD+cD2为最优树高曲线模型，其中，红松、椴树和榆树也可用Schumacher型H=1.3+aDb来描述，色木也可用幂函数型H=aDb来描述，白桦可用双曲线型H=aD/(D+b)来描述;而云杉则以双曲线型H=1.3+aDb为最优树高曲线模型，也可用抛物线型H=a=bD+cD2来描述.

3.2 过伐林分主要树种树高曲线模型的确定

利用统计之林(ForStat)2.1软件对过伐林分中主要树种红松、椴树、榆树、色木、云杉、水，胡，黄、冷杉和桦树树高与胸径的关系进行了非线性度量误差模型分析，结果见表4.

表3 白桦林分主要树种非线性度量误差模型分析结果

表4 过伐林主要树种拟合结果

从表4中由决定系数R2和残差平方和SSE可以看出:在过伐林分中，红松、云杉、水胡黄、白桦都抛物线型H=a+bD+cD2为最优树高曲线模型，其中云杉也可用双曲线型H=aD/(D+b)来描述;而椴树、榆树和色木以幂函数型H=aDb为最优树高曲线模型，其中，色木也可用Schumacher型H=1.3+aDb来描述;冷杉则以对数型H=1.3+aDb为最优树高曲线模型，但也可用抛物线型H=a+bD+cD2来描述.

3.3 柞木林分主要树种树高曲线模型的确定

统计之林(ForStat)2.1软件对柞木林主要树种红松和柞木标准木为对象，进行了回归分析，结果见表5.

表5 柞木林主要树种拟合结果

从表5中由决定系数R2和残差平方和SSE可以看出:在柞木林分中，红松以抛物线型H=a+bD+cD2为最优树高曲线模型，也可用Schumacher型H=1.3+aDb来描述;而柞木以幂函数型H=aDb为最优模型，也可用抛物线型H=a+bD+cD2或 Schumacher型H=1.3+aDb来描述.

4 结论

(1)在阔叶红松林区中，红松、白桦的树高曲线模型受林分类型的影响较小，用抛物线型能较好地模拟当地红松和白桦的树高与胸径的关系.在白桦林分和柞木林分中虽然红松主要以幼树为主，但也以 Schumacher型H=1.3+aDb为最优.

(2)在阔叶红松林区中，椴树、色木、云杉和榆树的树高曲线模型受林分类型的影响较大，在不同的林分中，它们的胸径树高曲线模型有所不同.

(3)在白桦林分和柞木林分中，由于水曲柳、胡桃楸、黄菠萝、冷杉和柞木数量较少，还无法统计分析出它们的树高曲线模型在不同林分中的差异.水曲柳、胡桃楸、黄菠萝以抛物线型H=a+bD+cD2为最优树高曲线模型;柞木以幂函数型H=aDb为最优树高曲线模型，也可用抛物线型H=a+bD+cD2或 Schumacher型H=1.3+aDb来描述;冷杉以Schumacher型H=1.3+aDb为最优树高曲线模型，也可用抛物线型H=a+bD+cD2来描述.

(4)该文在研究不同林分类型中主要树种的树高曲线最优模型中，没有考虑林分密度等因素.

［1］ 向玮，吕勇，邱林.湖南黄丰桥林场杉木树高曲线模拟研制.中南林业调查规划，2007(1):16-18.

［2］ 孙圆，王万江.江苏省杨树树高曲线模型的研制.林业科技开发，2005(5):31-34.

［3］ 曾翀，雷相东，刘宪钊，等.落叶松云冷杉林单木树高曲线的研究.林业科学研究，2009(2):182-189.

［4］ 晓琳，郭斌.柞树树高与胸径相关关系的研究.森林工程，2012(6):18-21.

［5］ 唐守正，李勇.生物数学模型的统计学基础.北京:科学出版社，2002.

［6］ 李永慈，唐守正.度量误差对模型参数估计值的影响及参数估计方法的比较研究［J］.生物数学学报，2006，21(2):285-290.

［7］ 唐守正，张淑梅.度量误差模型及其应用［J］.生物数学学报，1998，13(2):161-166.